Ошибка.
Попробуйте повторить позже
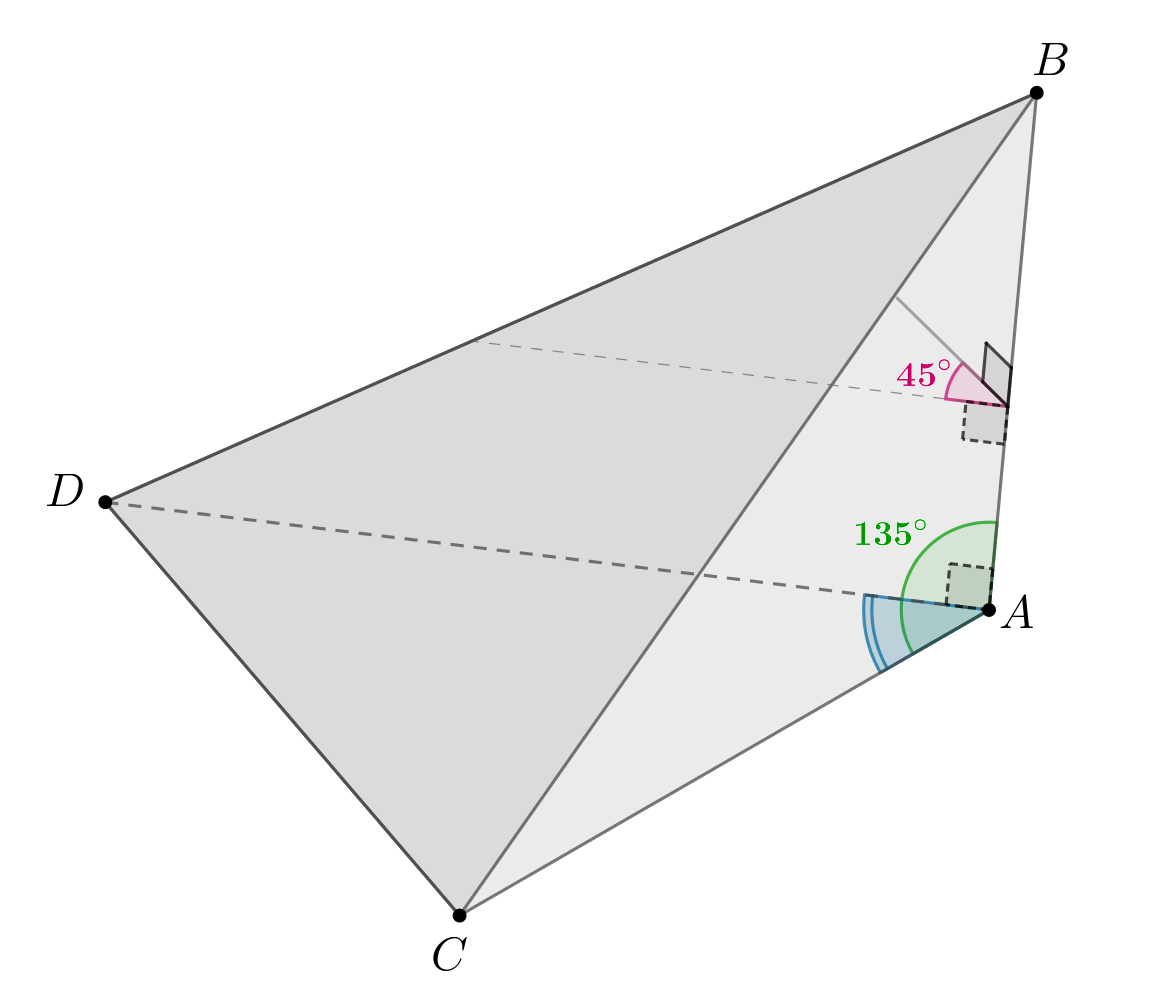
Прямоугольный треугольник с катетами
и
является
основанием пирамиды
Высота пирамиды равна
угол
—
прямой, тангенс угла между гранями
и
равен
а) Докажите, что угол между плоскостью и плоскостью основания
равен
б) Найдите площадь грани
Источники:
а) Проведем в плоскости
Тогда
следовательно,
Значит.
Также из этого построения следует, что следовательно, если
провести
то
и
Следовательно,
то есть
— высота пирамиды
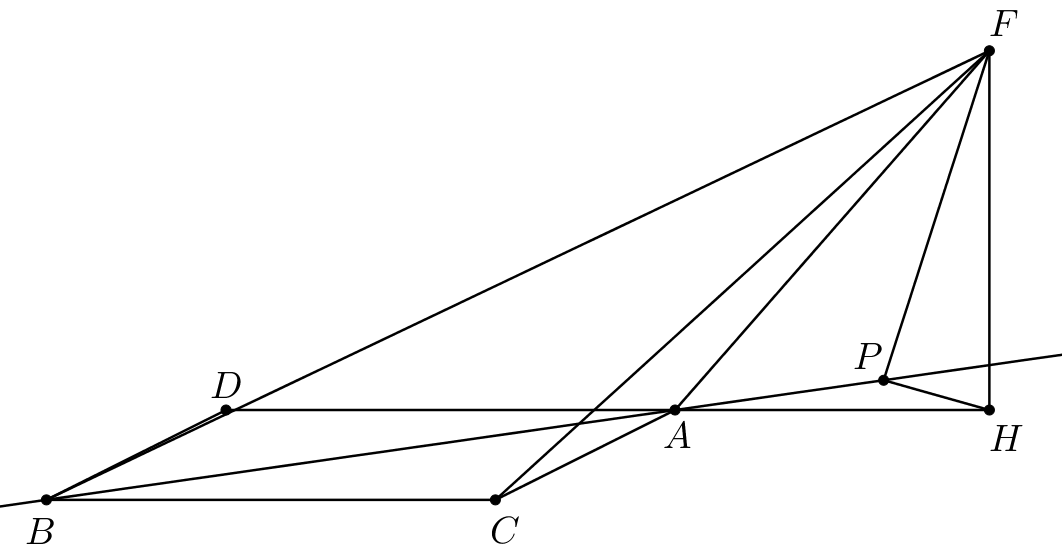
Тогда
Проведем Тогда по теореме о трех перпендикулярах
следовательно,
Требуется доказать, что
Рассмотрим
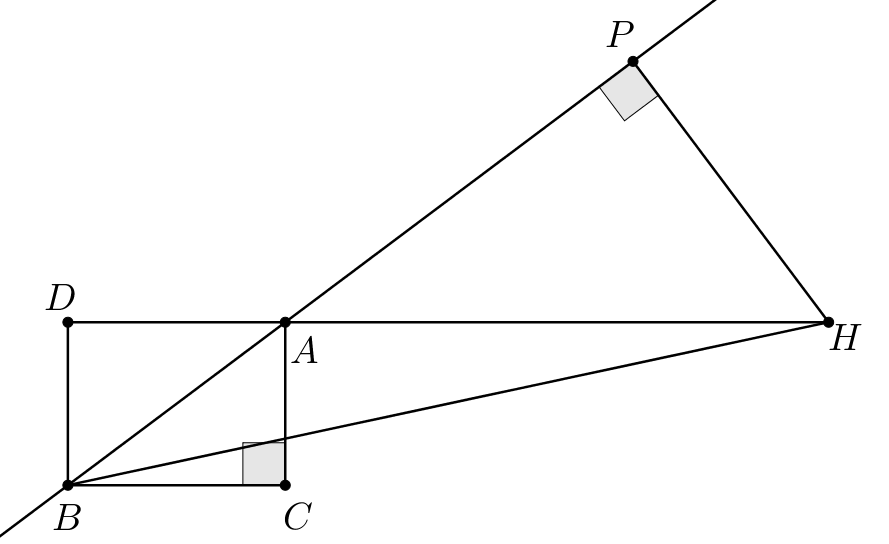
По теореме Пифагора в треугольнике имеем
Найдем
Так
как
как соответственные при
и секущей
то
значит,
Тогда
Что и требовалось доказать.
б) — проекция
на плоскость

Следовательно,
Заметим, что в отрезок
— высота к основанию
следовательно,
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
Основание пирамиды — равнобедренный прямоугольный треугольник. Каждый из
двугранных углов при основании равен Высота пирамиды равна
. Найдите
площадь основания.
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми углами, то основание высоты пирамиды — центр вписанной в основание пирамиды окружности. Докажем это.
Опустим высоту пирамиды
к основанию
Опустим
перпендикуляры
на стороны
По ТТП
перпендикулярны сторонам треугольника
Тогда по определению
— линейные углы двугранных углов между
боковыми гранями пирамиды и ее основанием. Следовательно, по общему
катету и острому углу
. Следовательно,
Таким образом,
— центр вписанной в
окружности радиуса
.
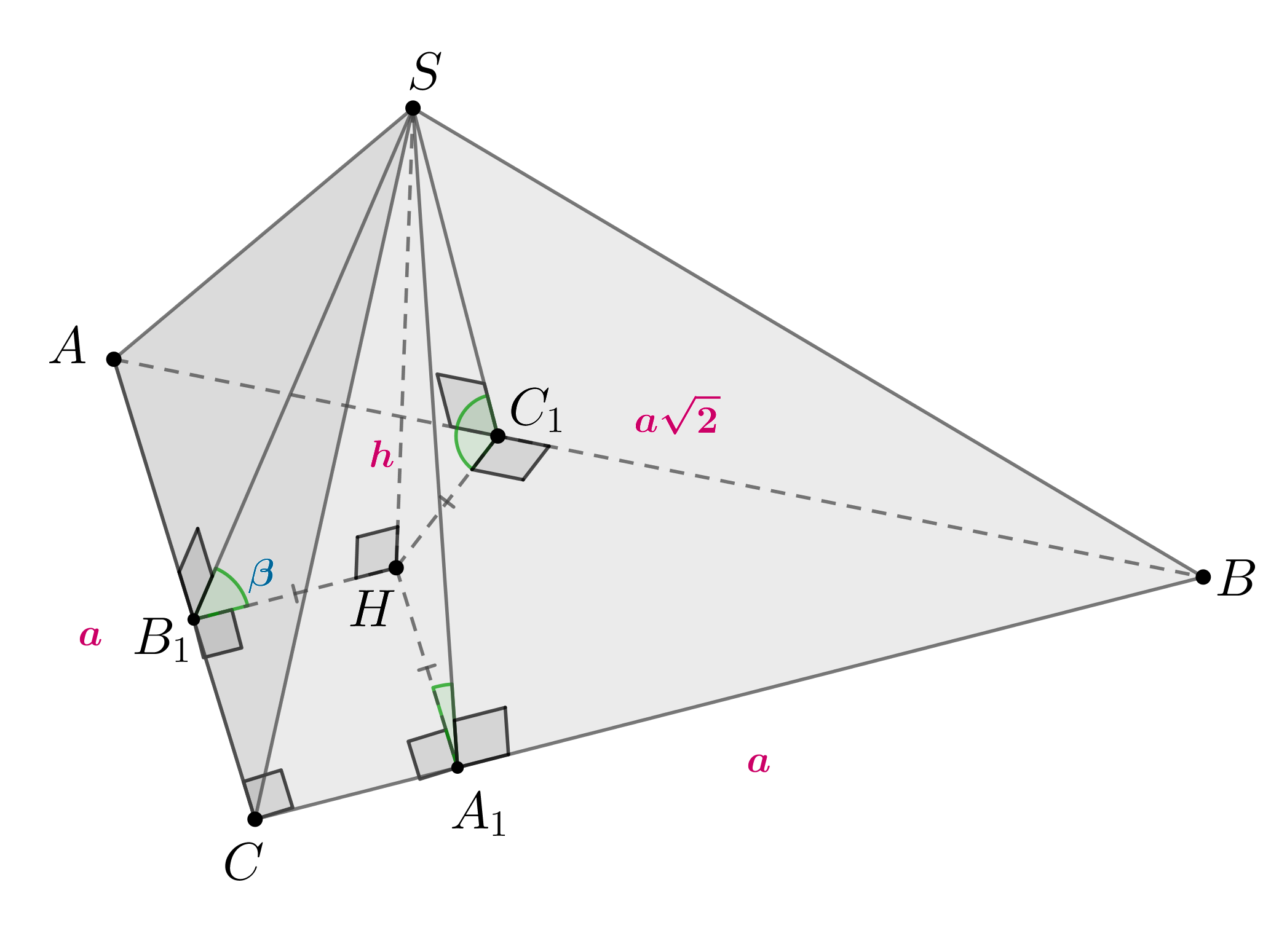
Так как прямоугольный и равнобедренный, то
Также
— квадрат,
и
как отрезки
касательных, следовательно,
Следовательно,
Ошибка.
Попробуйте повторить позже
Основание пирамиды — треугольник со сторонами 13, 14 и 15. Все двугранные
углы при сторонах основания равны Найдите высоту пирамиды.
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми углами, то основание высоты пирамиды — центр вписанной в основание пирамиды окружности. Докажем это.
Опустим высоту пирамиды
к основанию
Опустим
перпендикуляры
на стороны
По теореме о трех
перпендикулярах отрезки
перпендикулярны сторонам
треугольника
Тогда по определению — линейные углы
двугранных углов, образуемых боковыми гранями пирамиды и ее основанием.
Следовательно, по общему катету и острому углу
Следовательно,
Таким образом, точка
— центр
вписанной в
окружности радиуса
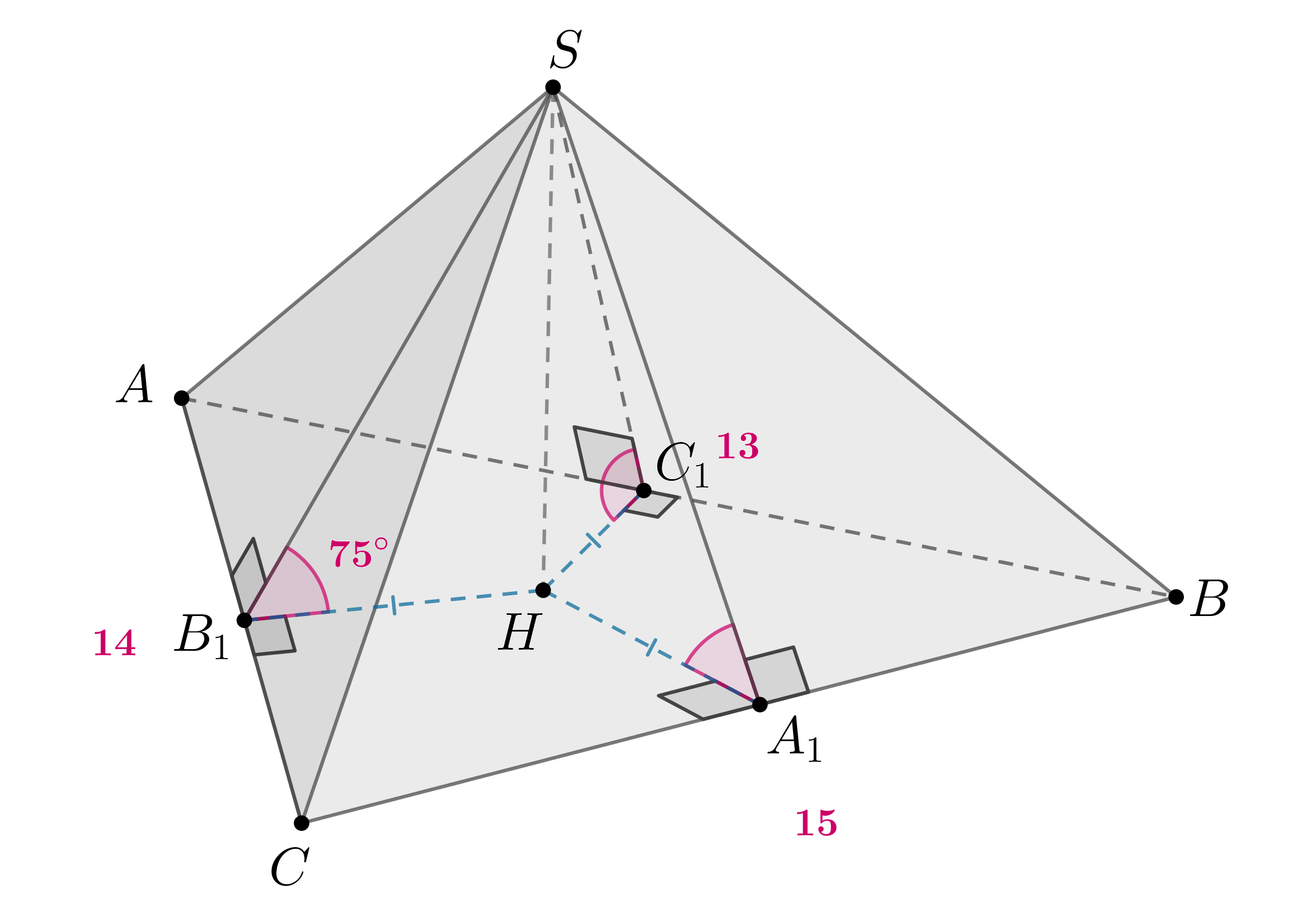
Будем искать по формуле
Площадь равна
Тогда
Так как то найдем
Следовательно,
Ошибка.
Попробуйте повторить позже
Основанием пирамиды служит треугольник со сторонами 10, 10 и 12. Все боковые
грани пирамиды наклонены к плоскости основания под углом Найдите
высоту пирамиды.
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми углами, то основание высоты пирамиды — центр вписанной в основание пирамиды окружности. Докажем это.
Опустим высоту пирамиды
к основанию
Опустим
перпендикуляры
на стороны
По теореме о трех
перпендикулярах
перпендикулярны сторонам треугольника
Тогда по определению — линейные углы
двугранных углов, образуемых боковыми гранями пирамиды и ее основанием.
Следовательно, по общему катету и острому углу
Следовательно,
Таким образом,
— центр
вписанной в
окружности радиуса
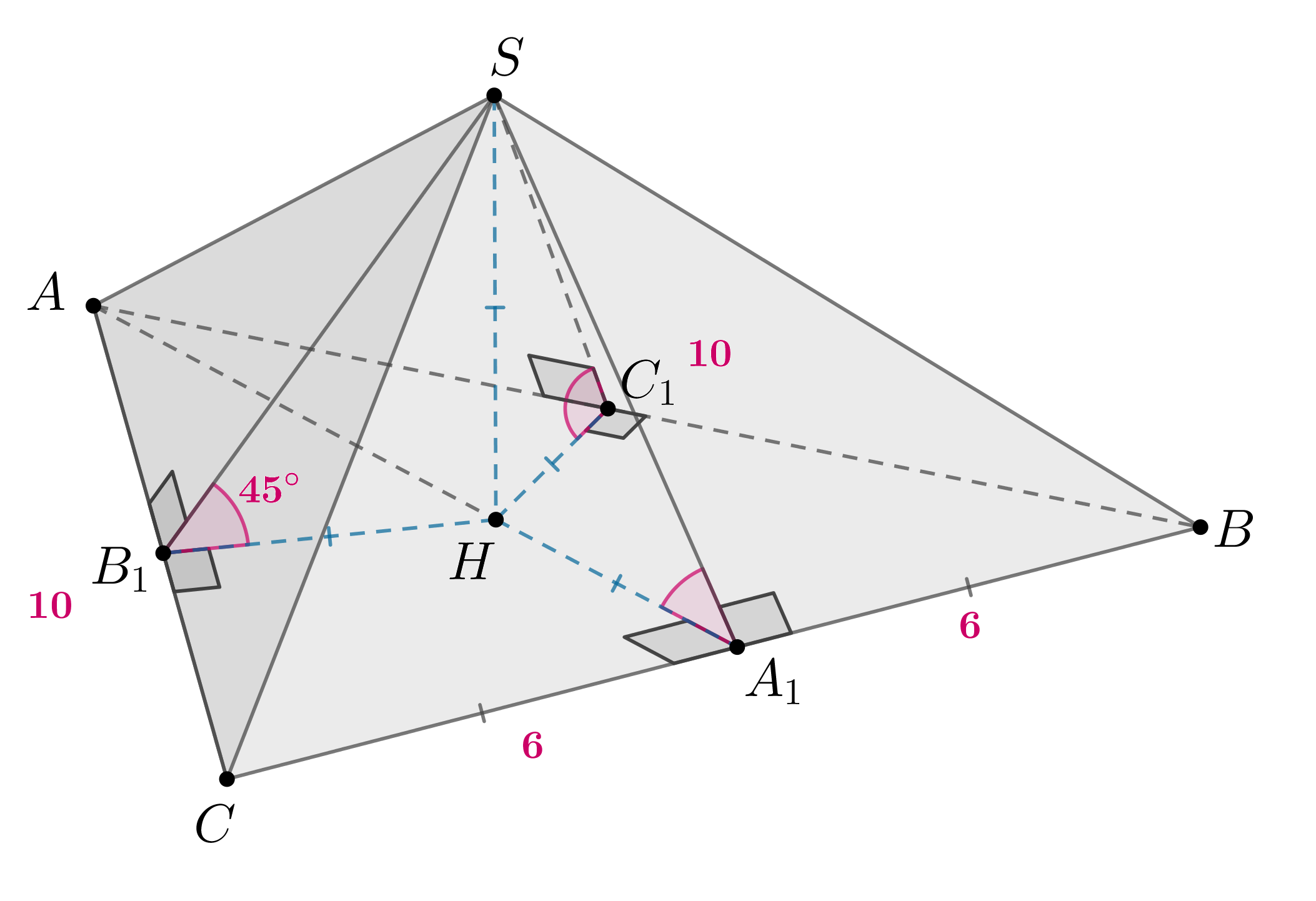
Так как равнобедренный, то точка
лежит на высоте
треугольника, проведенной к основанию.
По теореме Пифагора в треугольнике имеем:
Найдем радиус вписанной окружности через площадь и периметр основания:
Тогда в равнобедренном прямоугольном треугольнке имеем:
Ошибка.
Попробуйте повторить позже
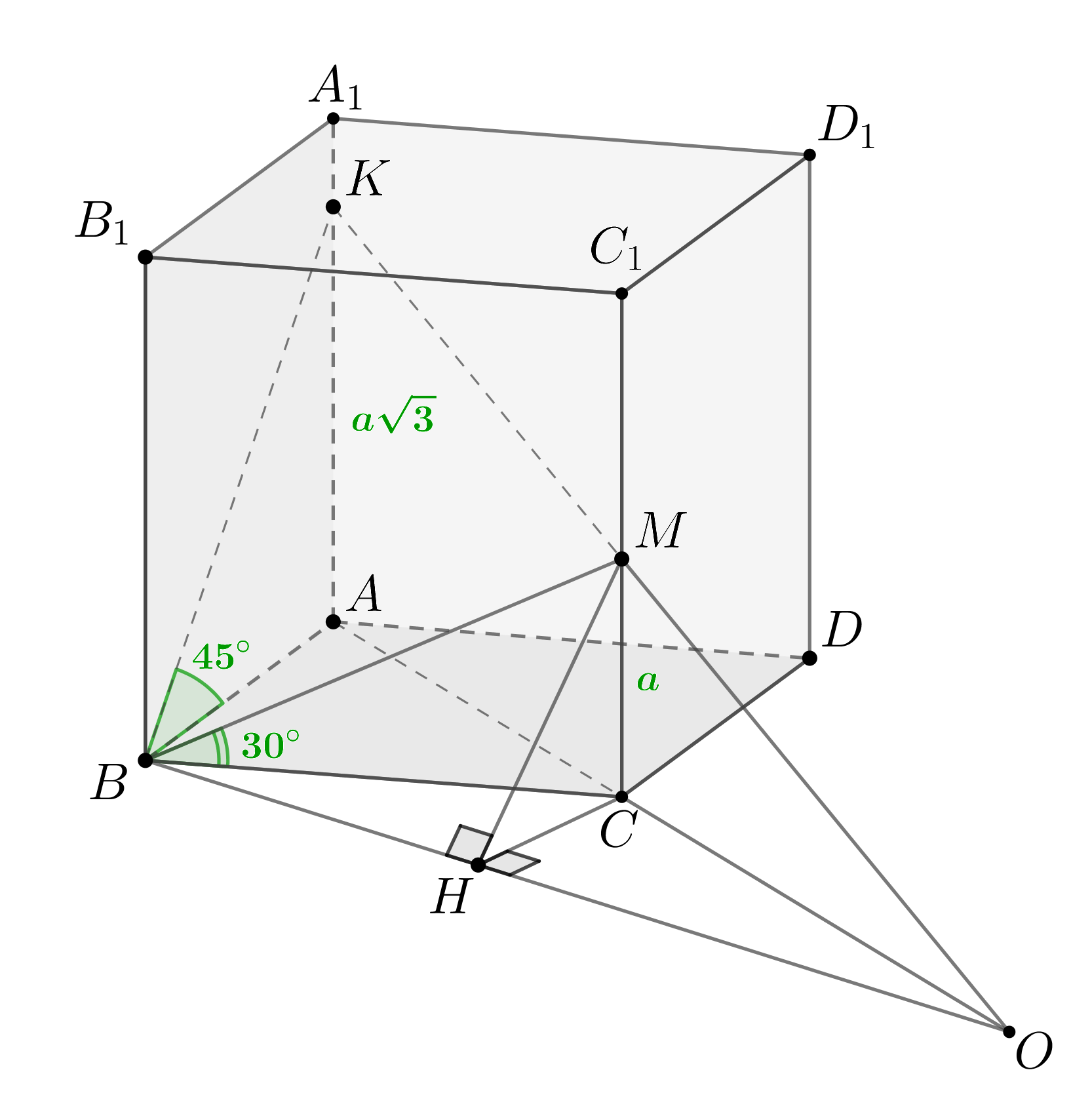
Основанием наклонной призмы служит прямоугольник со сторонами и
Две
смежные боковые грани составляют с основанием острые углы, равные
и
соответственно. Найдите объем призмы, если боковое ребро равно
Пусть Проведем
Тогда по ТТП
Следовательно, по определению
— линейные углы двугранных углов между боковыми гранями и
основанием.
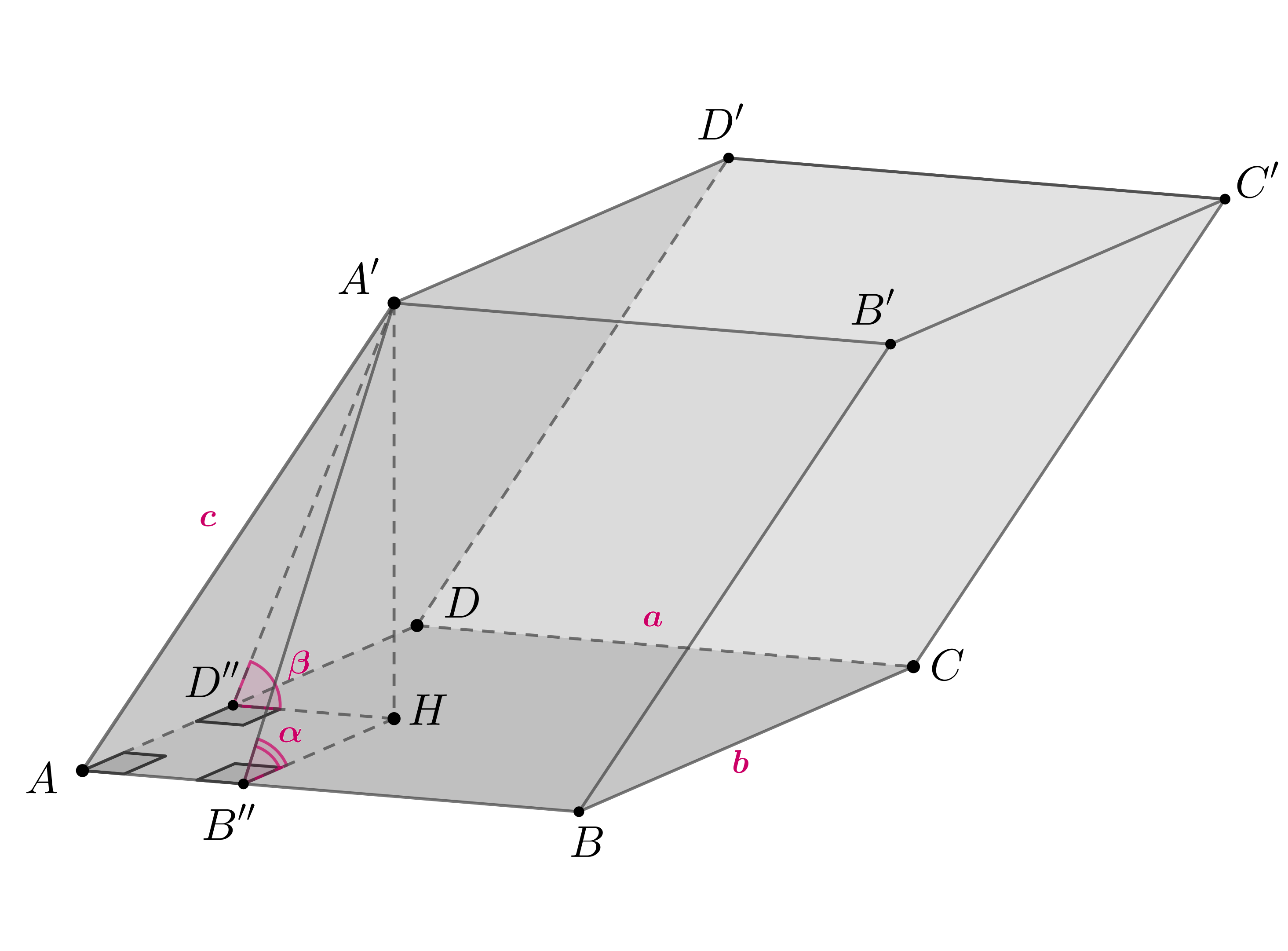
Пусть
— четырехугольник, три угла которого прямые,
следовательно, это прямоугольник. Таким образом,
Так как , то
Следовательно,
Ошибка.
Попробуйте повторить позже
В правильной треугольной призме через сторону основания
и вершину
проведена плоскость. Сторона основания призмы
равна
угол наклона сечения к основанию равен
Найдите объем
призмы.
Проведем Тогда по ТТП
Следовательно,
—
угол наклона плоскости
к плоскости основания
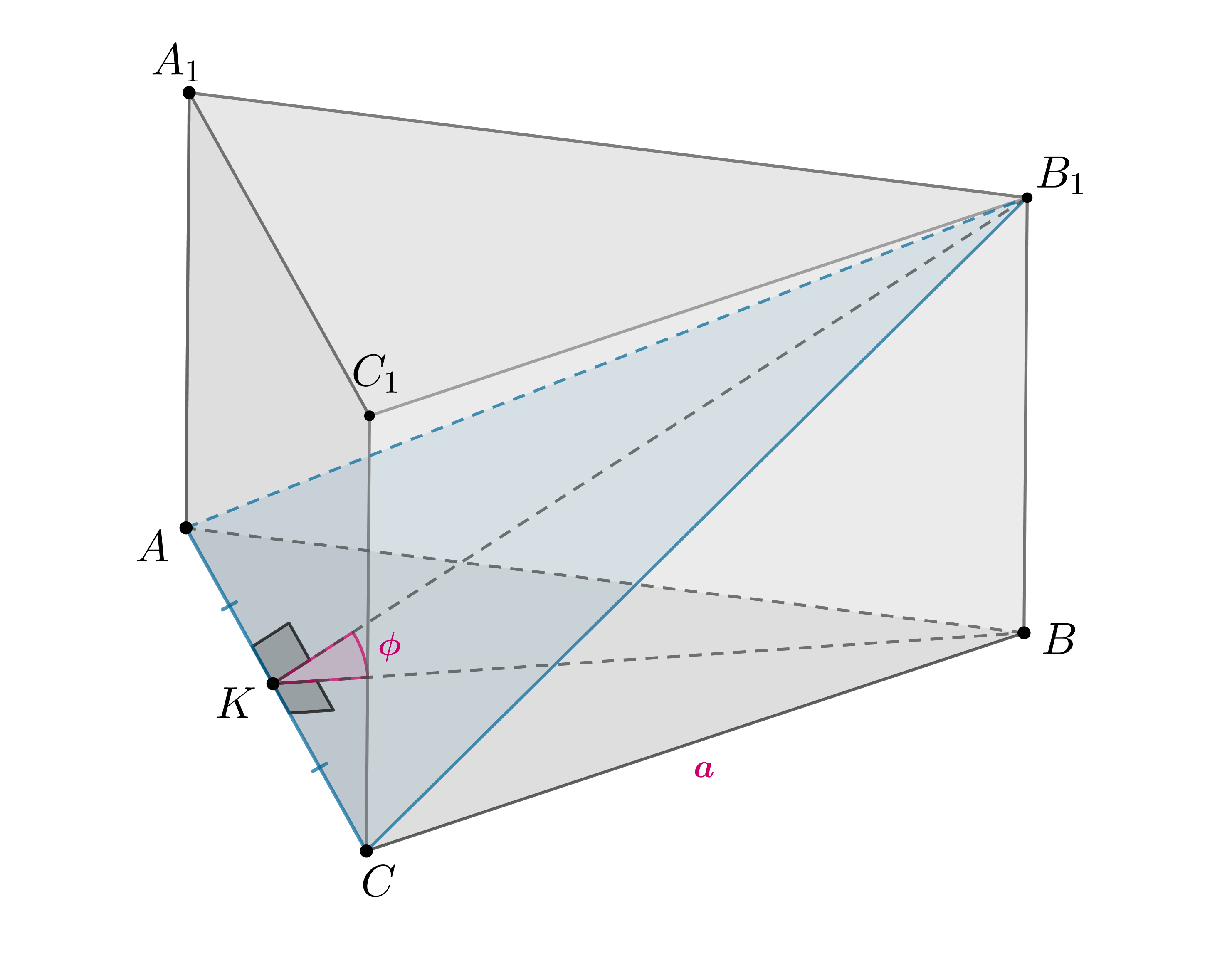
Так как равносторонний и
то
Из прямоугольного
имеем
откуда
Следовательно, объем призмы равен
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде известны ребра:
Найдите угол между плоскостями
и
Проведем Тогда по теореме о трех перпендикулярах наклонная
Следовательно,
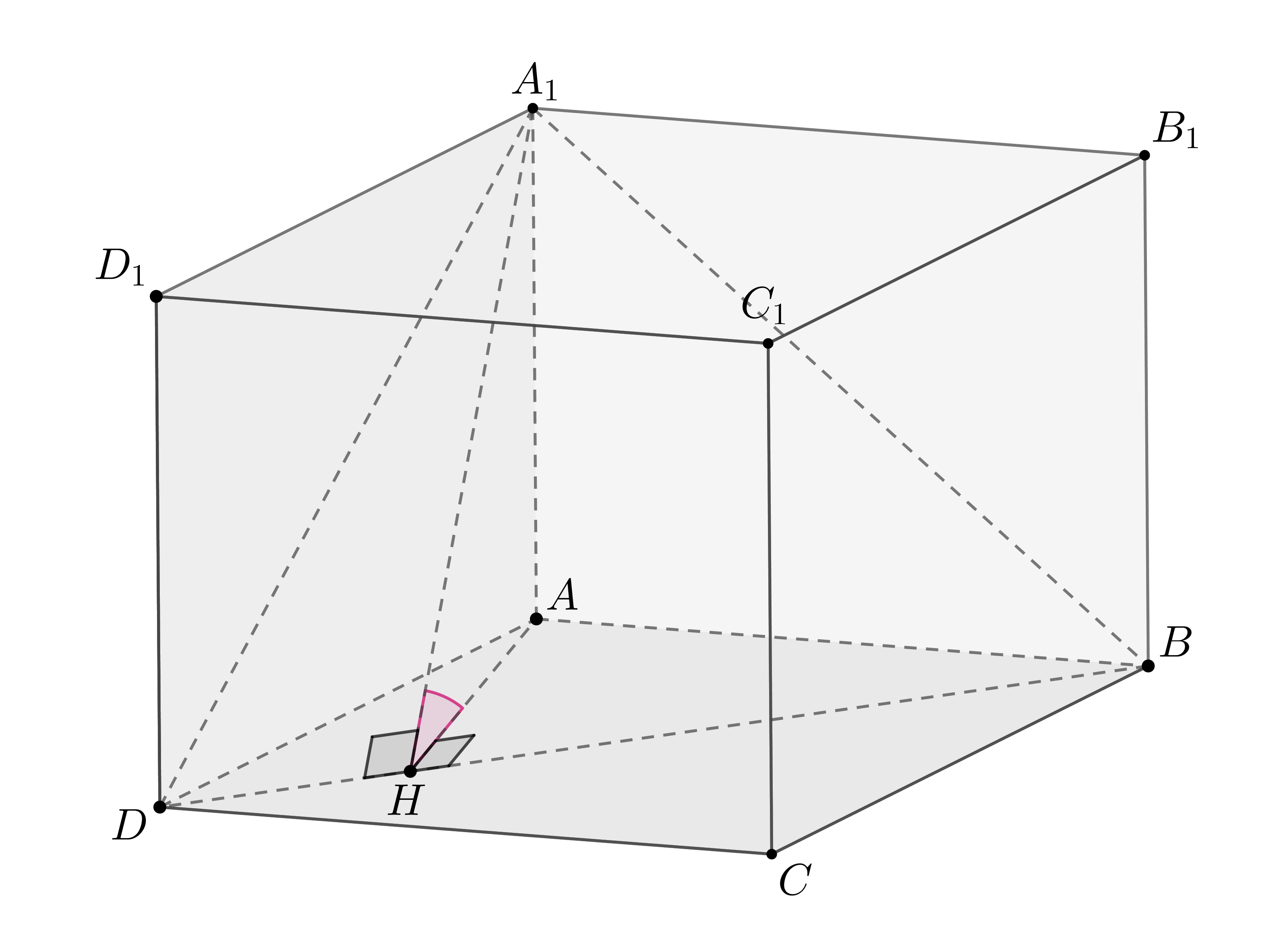
По теореме Пифагора в треугольнике имеем:
Так как то
Тогда
Ошибка.
Попробуйте повторить позже
Докажите, что плоскость, делящая пополам двугранный угол при ребре тетраэдра, делит противоположное ребро на части, пропорциональные площадям граней, заключающих этот угол.
Пусть ,
по ТТП
, следовательно,
— линейный угол двугранного угла между плоскостями
и
. Пусть
, тогда плоскость
(делящая угол между
и
пополам) пересекает
в точке
:
— биссектриса
.
Пусть
, тогда
— сечение пирамиды плоскостью
.
Требуется доказать, что
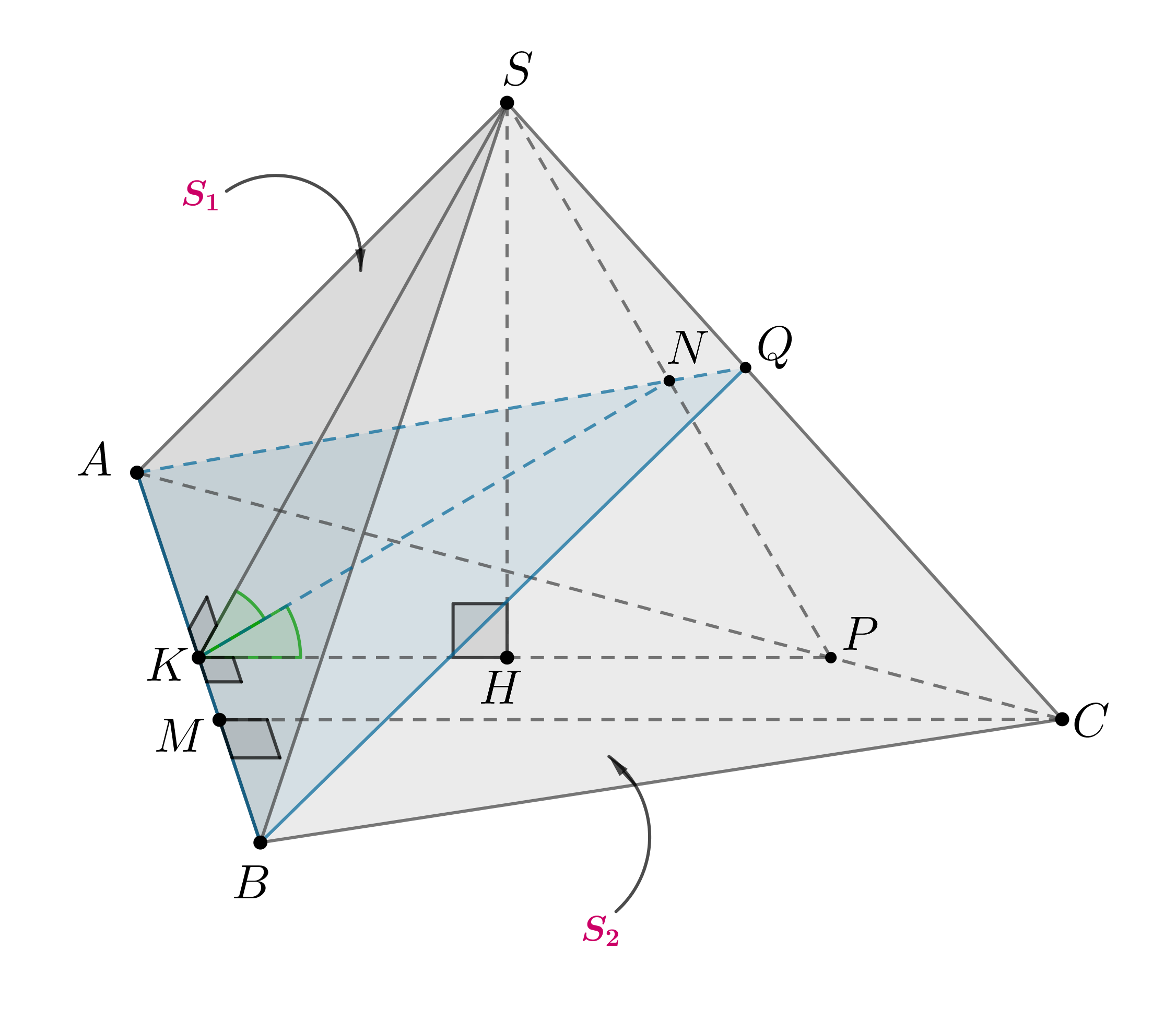
Так как — биссектриса
, то
По теореме Менелая для и прямой
:
Проведем . Тогда
и
,
следовательно,
Чтд.
Доказательство
Ошибка.
Попробуйте повторить позже
Докажите, что если и
— площади двух граней тетраэдра,
— их общее
ребро, а
— двугранный угол между ними, то объем этого тетраэдра
равен
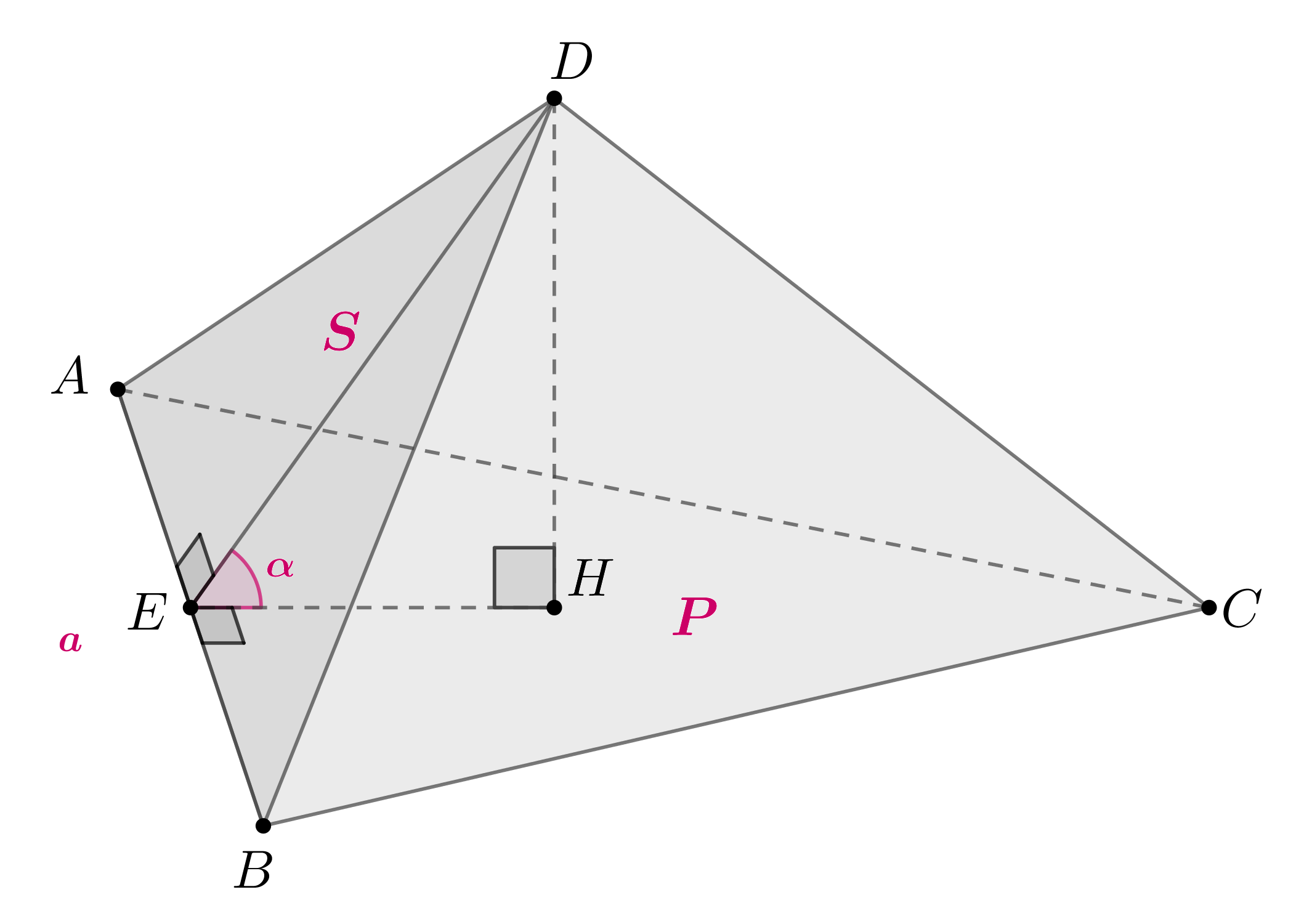
— высота тетраэдра, проведенная к грани площадью
,
,
, тогда по ТТП наклонная
, следовательно,
. Так
как
, то
. Из прямоугольного
имеем
, следовательно,
Мы рассмотрели случай, когда . В случай, если
, точка
находится вне грани
и работать мы будем с тем же треугольником
,
но с его углом
, синус которого равен синусу угла
. Следовательно,
формула останется прежней.
Доказательство
Ошибка.
Попробуйте повторить позже
В пирамиде с углом
точка
— проекция точки
на
плоскость
Найдите величину угла между плоскостями
и

— линия пересечения плоскостей
и
. Следовательно, так как
,
— линейный угол двугранного угла
между этими плоскостями. Если он острый или прямой, то он равен углу между
этими плоскостями, если он тупой, то смежный с ним угол равен углу между этими
плоскостями, следовательно, угол между
и
равен
, если
, и
, если
.
, если
, и
, если
Ошибка.
Попробуйте повторить позже
Пусть — проекция точки
на данную плоскость,
. Через точку
проходит другая плоскость, образующая с данной плоскостью угол
и
пересекающая ее по прямой
Найдите расстояние от точки
до прямой
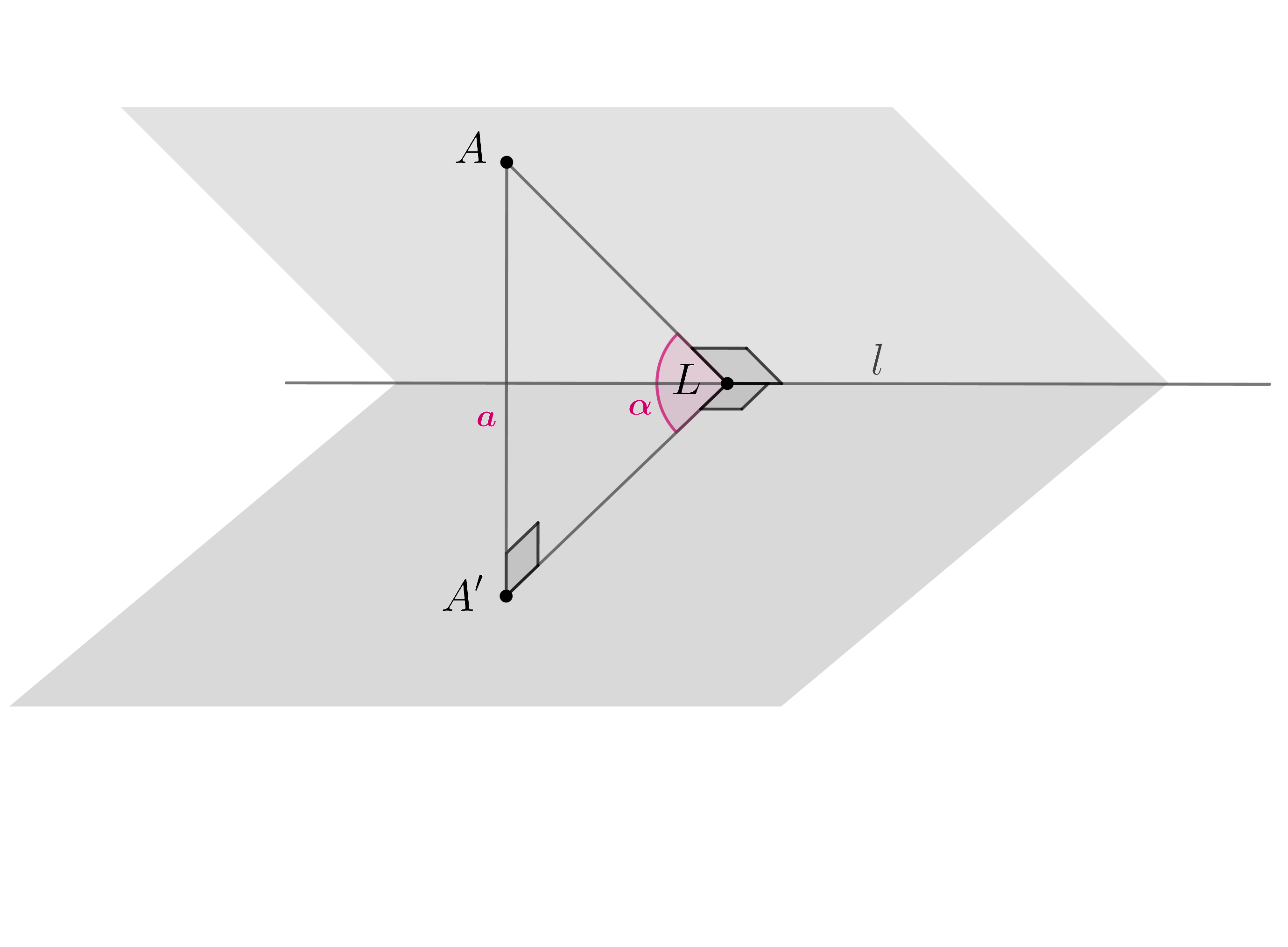
— перпендикуляр к плоскости, содержащей точку
. Проведем
,
тогда по ТТП наклонная
. Следовательно,
— линейный
угол двугранного угла между двумя плоскостями, то есть
.
Тогда
Ошибка.
Попробуйте повторить позже
Двугранный угол при ребре тетраэдра
равен
Найдите
если
По теореме косинусов для трехгранного угла (id41318), где —
двугранный угол при ребре
:
По теореме косинусов для
Ошибка.
Попробуйте повторить позже
Двугранный угол при ребре тетраэдра
равен
Найдите
,
если
и
Ошибка.
Попробуйте повторить позже
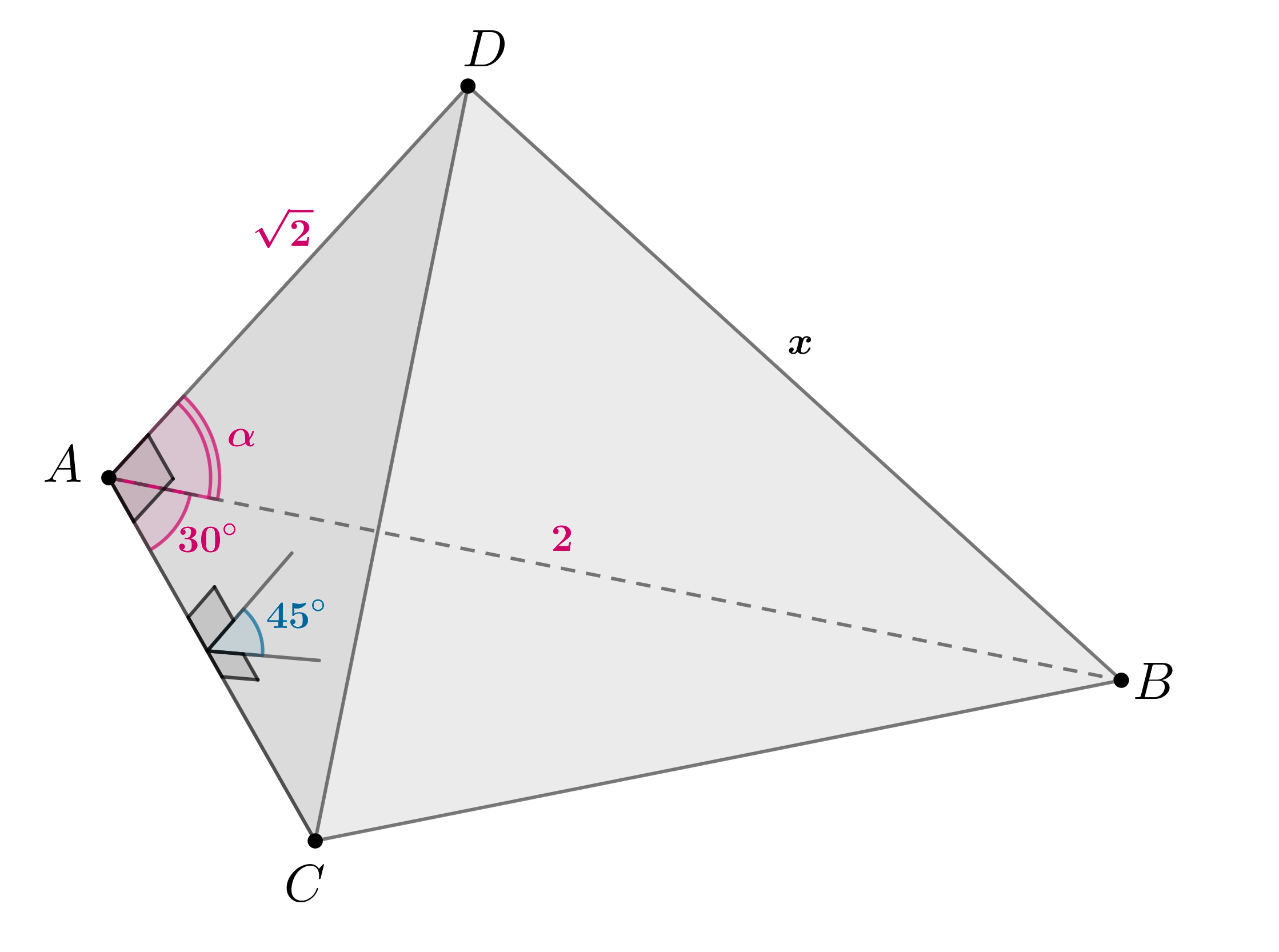
Основанием прямой призмы служит ромб с углом
На
боковых ребрах
и
взяты такие точки
и
соответственно,
что угол между прямыми
и
равен
, а угол между прямыми
и
равен
Найдите угол между плоскостями
и
Проведем через точку прямые параллельно прямым
и
и
переобозначим точки. Пусть эти прямые пересекают ребра
и
в точках
и
соответственно, как показано на рисунке. Тогда
Построим линейный угол двугранного угла, образуемого плоскостями
и
Для этого нужно найти линию пересечения этих плоскостей.
Пусть тогда
— линия пересечения плоскостей
и
Проведем
Тогда по ТТП
Следовательно,
— искомый линейный угол.
Пусть Тогда
следовательно,
Так как то
, следовательно,
правильный,
то есть

Из подобия имеем:
Тогда
По теореме косинусов для
По теореме синусов для этого же треугольника:
Из имеем:
Следовательно, из
Ошибка.
Попробуйте повторить позже
В правильной пирамиде с вершиной
боковое ребро равно
,
а двугранный угол при этом ребре равен
Найдите площадь сечения
пирамиды плоскостью, проходящей через точки
и середину
ребра
— правильная четырехугольная пирамида, следовательно, в
основании лежит квадрат, боковые ребра равны между собой, а основание
высоты
пирамиды — точка
— точка пересечения диагоналей
Проведем . Так как боковые грани — равные равнобендренные
треугольники, то
. Следовательно,
— двугранный угол при
боковом ребре пирамиды.
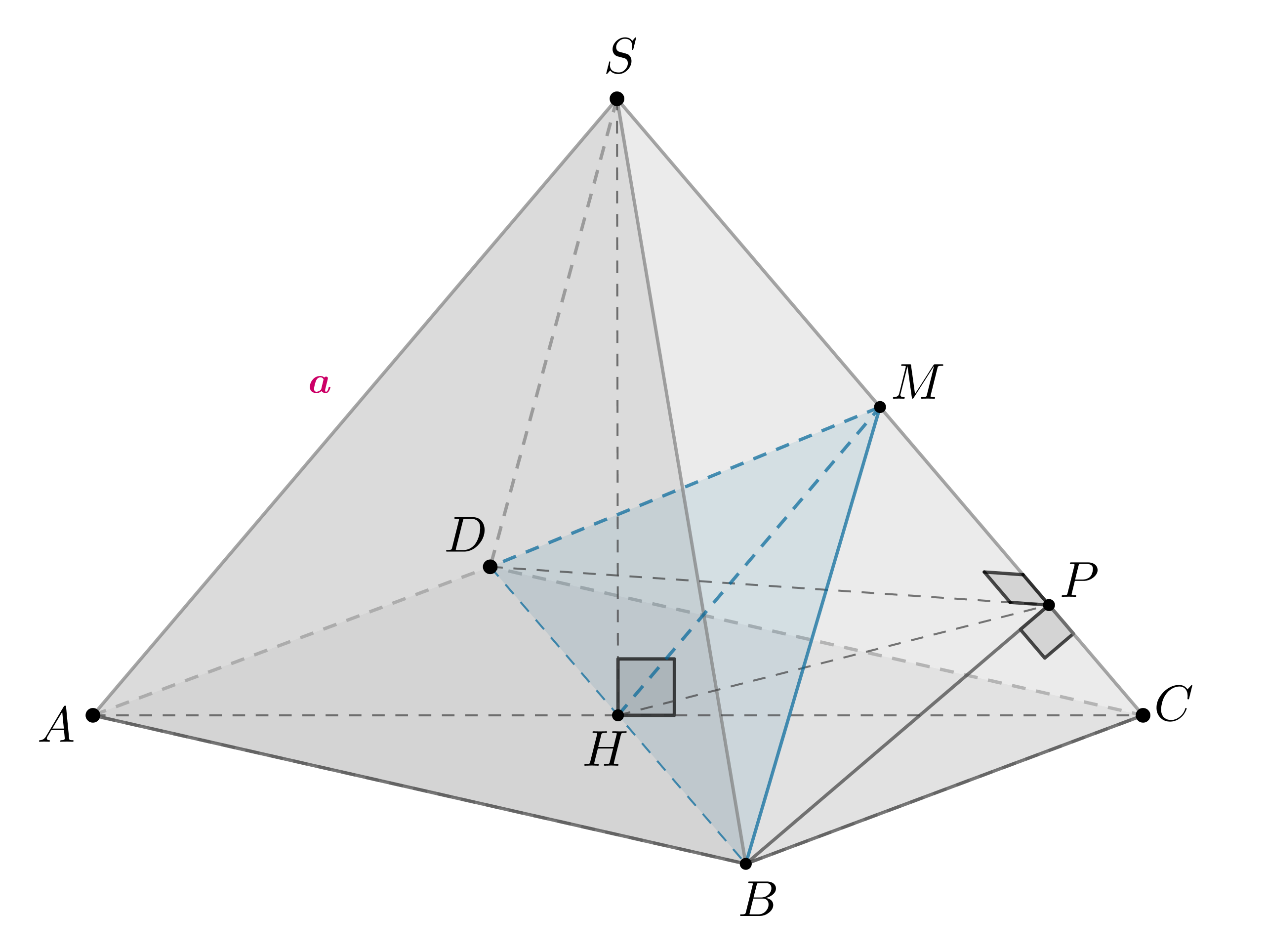
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то
она перпендикулярна этой плоскости, следовательно, любой прямой из этой
плоскости. Следовательно,
, то есть
—
высота прямоугольного треугольника
, проведенная к гипотенузе. Введем
. Так как
.
— проекция
на плоскость
. Так как
по
ТТП
Так как
— медиана
прямоугольного треугольника, проведенная к гипотенузе, то
Ошибка.
Попробуйте повторить позже
Найдите объем правильной четырехугольной пирамиды с высотой и
двугранным углом
при боковом ребре.
— правильная четырехугольная пирамида, следовательно, в
основании лежит квадрат, боковые ребра равны между собой, а основание
высоты
пирамиды — точка
— точка пересечения диагоналей
Проведем . Так как боковые грани — равные равнобендренные
треугольники, то
. Следовательно,
— двугранный угол при
боковом ребре пирамиды. Введем
.
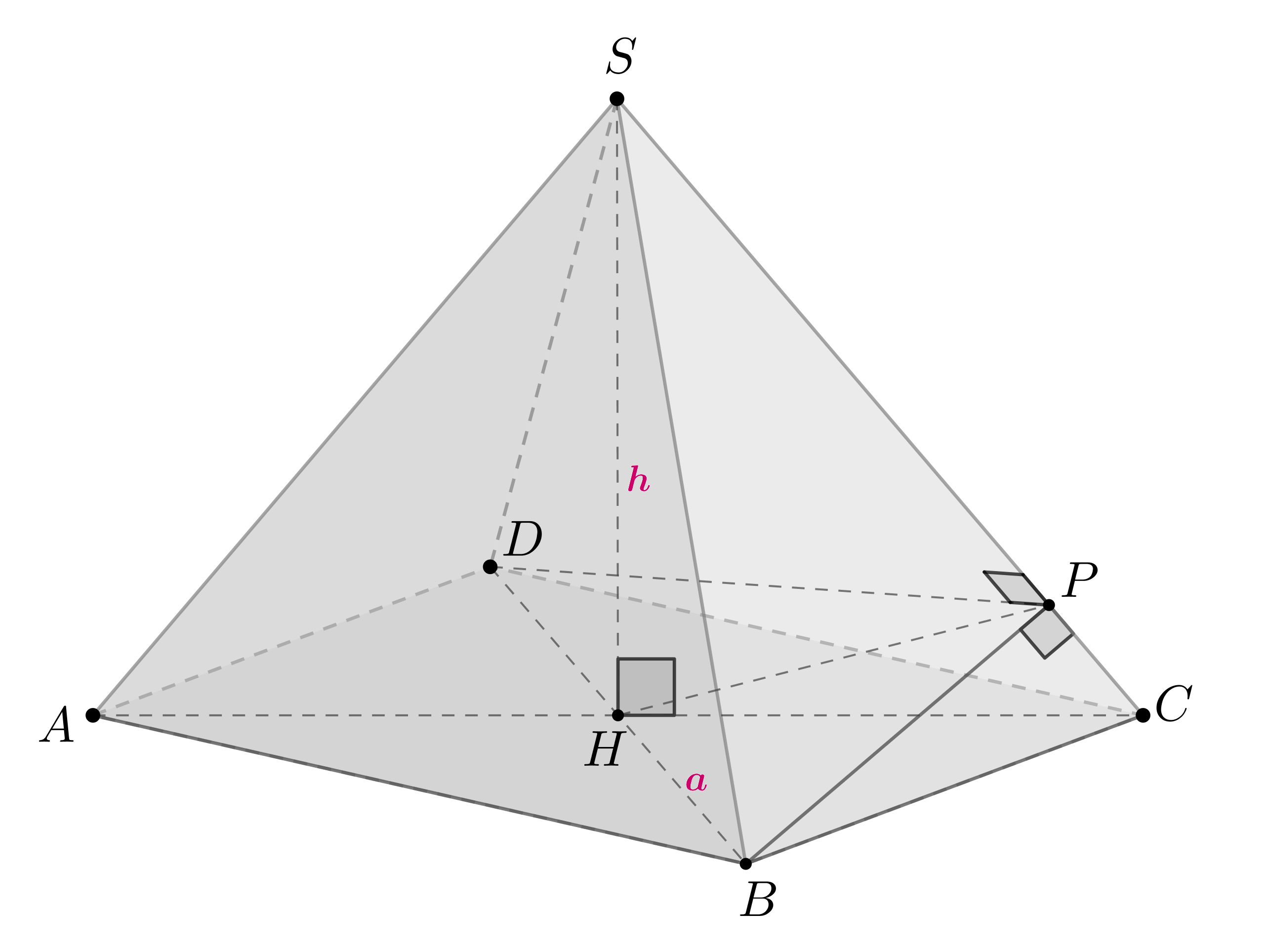
Если прямая перпендикулярна двум пересекающимся прямым плоскости, то
она перпендикулярна этой плоскости, следовательно, любой прямой из этой
плоскости. Следовательно,
, то есть
—
высота прямоугольного треугольника
, проведенная к гипотенузе. Так как
.
Так как , то
, следовательно,
Ошибка.
Попробуйте повторить позже
Основанием пирамиды с высотой
служит прямоугольный
треугольник
с гипотенузой
, а двугранные углы при ребрах основания
равны по
Найдите площадь боковой поверхности пирамиды, если
,
Если боковые грани пирамиды наклонены к плоскости основания под одинаковыми углами (двугранные углы при ребрах основания равны), то основание высоты пирамиды — центр вписанной в основание окружности. Докажем это.
Проведем ,
,
. Тогда по ТТП
,
,
. Следовательно,
—
двугранные углы при ребрах основания пирамиды. Следовательно,
как прямоугольные по катету и острому углу.
Отсюда
, то есть
— центр вписанной в
окружности радиуса
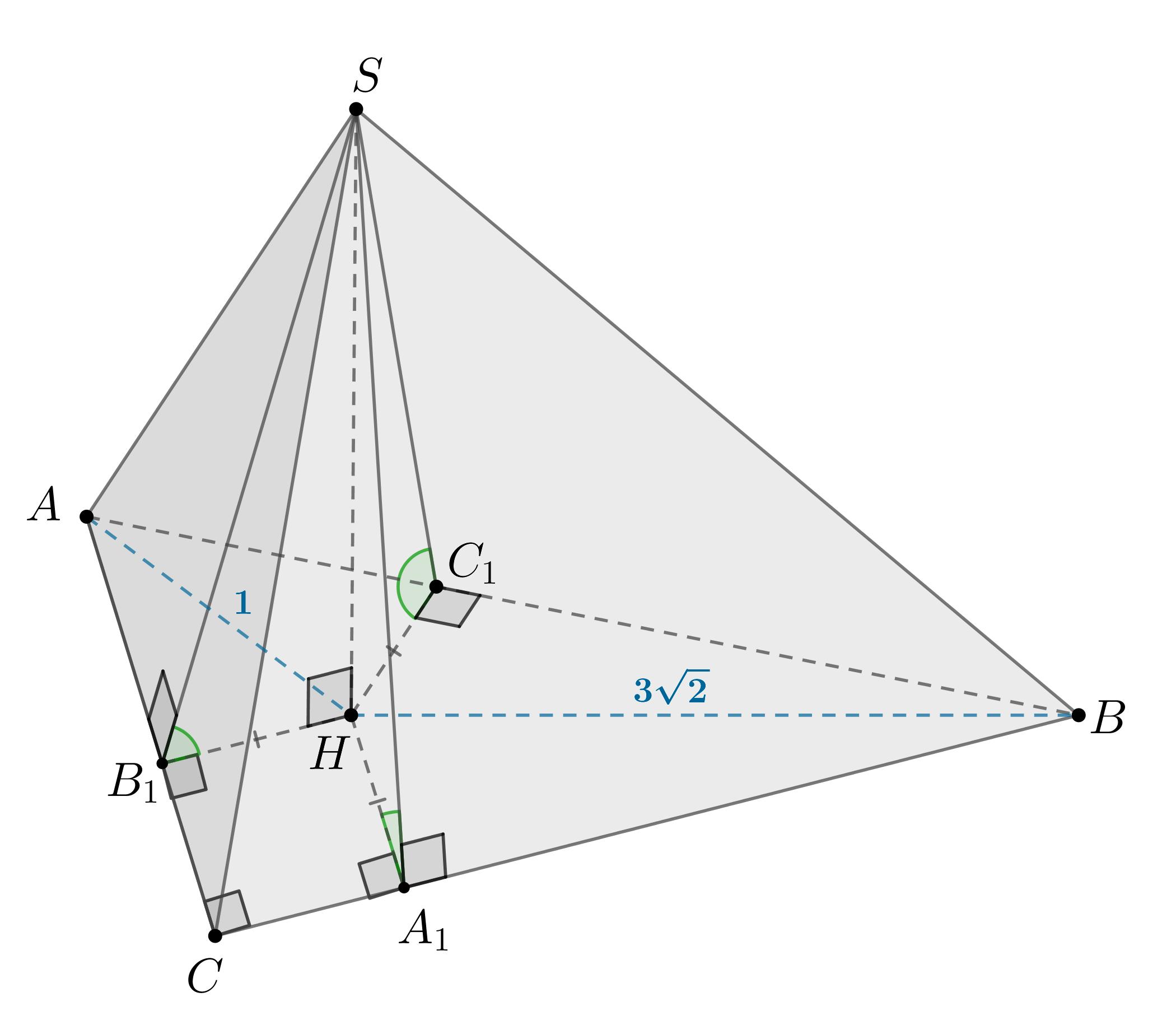
,
— отрезки биссектрис
и
.
Так как в прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла, то получаем равенство
Проверим, выполняется ли теорема Пифагора для при найденных
значениях
Заметим, что
,
как отрезки
касательных, проведенных к вписанной окружности из точек
соответственно.
Если , то
,
,
— верно.
Если , то
,
,
— неверно.
Следовательно, . Так как
то
. Так как из
выше приведенного равенства треугольников
, то площадь
боковой поверхности пирамиды равна
Ошибка.
Попробуйте повторить позже
Найдите двугранный угол при ребре основания правильной треугольной пирамиды,
если угол между ее боковыми ребрами равен
Пусть — правильная треугольная пирамида с вершиной
. Если
—
высота пирамиды, то
— точка пересечения высот правильного треугольника
, а боковые ребра равны между собой. Пусть
. Тогда по
ТТП
, следовательно,
— двугранный угол при ребре
.
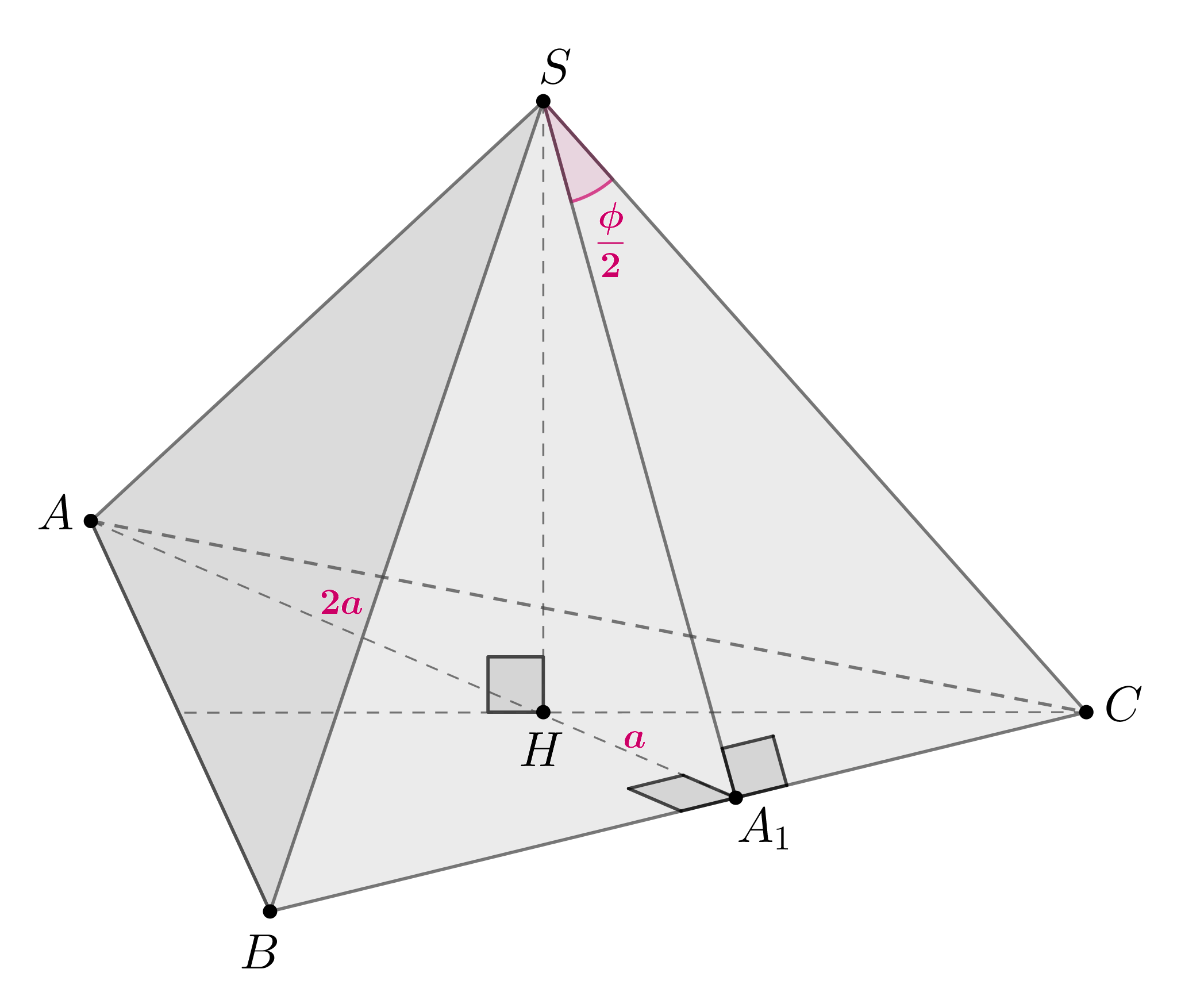
Пусть . Тогда
,
Из
имеем:
Тогда
Ошибка.
Попробуйте повторить позже
Докажите теорему косинусов для двугранного угла:
Двугранный угол между плоскостями и
, пересекающимися по
прямой
, равен
,
,
,
. Тогда верно
равенство
Проведем в плоскости отрезок
,
. Тогда
—
параллелограмм, следовательно,
, следовательно,
(
так как
). Следовательно,
Также
по построению
.
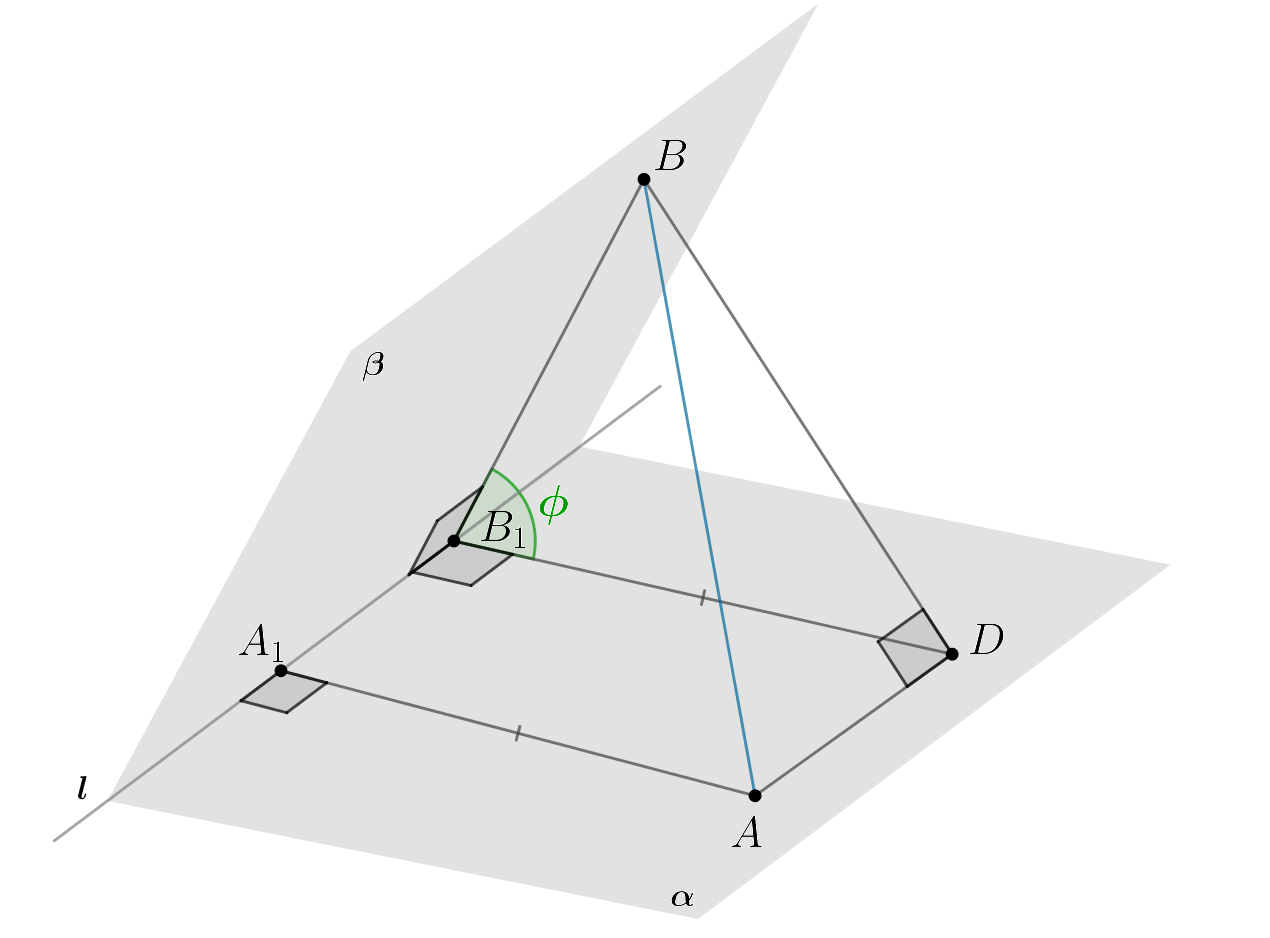
По теореме косинусов для
По теореме Пифагора из
Подставим первое равенство во второе, заменим на
,
на
и получим искомое равенство.
Ошибка.
Попробуйте повторить позже
Докажите теорему косинусов для трехгранного угла:
Косинус плоского угла трехгранного угла равен произведению косинусов
двух других плоских углов
и
трехгранного угла, сложенному с
произведением синусов этих углов на косинус двугранного угла
при
противолежащем ему ребре:
Пусть дан трехгранный угол ,
,
,
.
Двугранный угол при ребре
равен
.
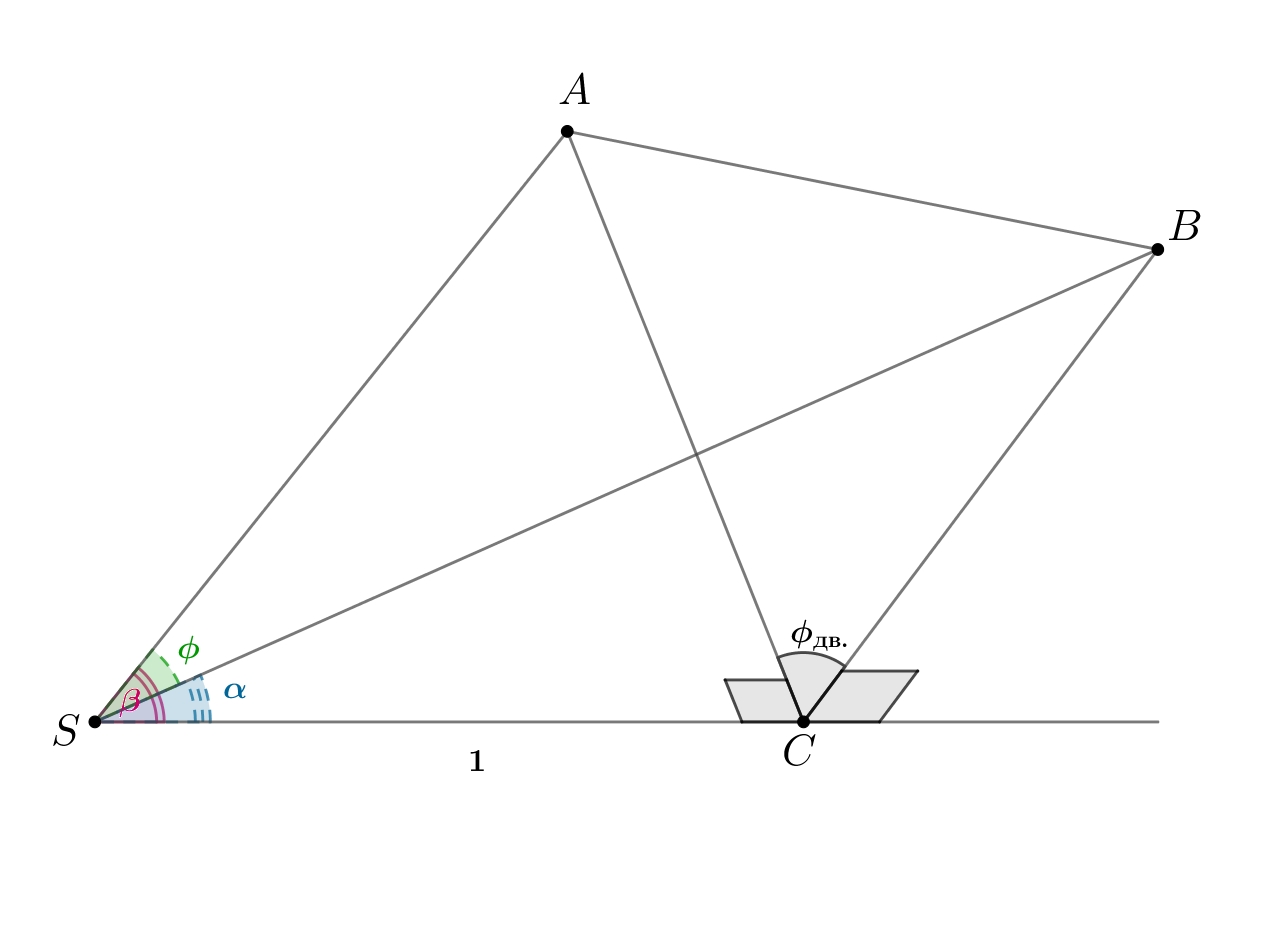
Выберем точки ,
и
на ребрах трехгранного угла таким образом,
чтобы
,
,
. Тогда
.
Из последних двух равенств, применяя формулы и
, получаем