Ошибка.
Попробуйте повторить позже
Найдите все числа вида которые можно представить в виде суммы двух точных квадратов.
Источники:
Подсказка 1
Может, можно выбрать какой-то хороший модуль, по которому можно провести сравнение для суммы двух квадратов и для числа такого вида?
Подсказка 2
Рассмотрите все по модулю 8)
Пусть для некоторых целых чисел
и
Если числа
и
чётны, то сумма их квадратов делится на
, а число
— нет. Таким образом, числа
и
могут быть только нечетными:
Следовательно, сумма
при делении на дает в остатке
С другой стороны, среди чисел вида только число
при делении на
дает в остатке
, поскольку если число двоек в этом
числе больше
, то
, при этом первое слагаемое полученной суммы делится на
, а второе при делении на
дает в остатке
Ошибка.
Попробуйте повторить позже
Докажите, что если выражение делится на
где
и
— целые, то
и
делятся на
Источники:
Подсказка 1
Вспомните, какие остатки по модулю 3 может давать квадрат целого числа?
Подсказка 2
Только 0 или 1! А если сумма таких дает 0, то какими они могут быть?)
Если целое число дает остаток
или
при делении на
то и
тоже. Если же
дает остаток
при делении на
то его
квадрат дает остаток
при делении на
То есть квадраты целых чисел дают остатки
и
при делении на
Тогда если выражение
делится на
то
и
делятся на
Ошибка.
Попробуйте повторить позже
Сколько существует натуральных чисел, меньших кратных
и не содержащих в записи цифр
Источники:
Подсказка 1
Давайте будем считать что наши числа трехзначные, просто мы можем ставить нули в начале. Подумайте, какие цифры могут быть на конце у такого числа, вариантов не так много)
Подсказка 2
Вспомните, что чтобы число делилось на 4, нужно чтобы число, составленное из последних двух цифр делилось на 4. А также можно заметить, что у нас нет нечетных цифр)
Подсказка 3
Да, на конце может быть только либо 0, либо 8! Осталось посчитать количество комбинаций последних двух цифр и по ним посчитать все комбинации из трех цифр!
По условию, эти числа записываются только цифрами Тогда трехзначные числа, кратные
могут иметь на конце в точности
вариантов:
При этом на первом месте в каждом из этих
вариантов может стоять одна из
возможных цифр:
В случае, если число двузначное, имеем
вариантов. А также
— однозначное натуральное число, кратное
Итого,
Ошибка.
Попробуйте повторить позже
Если взять три разные цифры, составить из них все шесть возможных двузначных чисел, записанных двумя разными
цифрами, и сложить эти числа, то получится Найдите эти цифры. Приведите все варианты и докажите, что других
нет.
Источники:
Подсказка 1
Предположим, что наши три цифры - a, b, c. Как можно выразить сумму всех наших двузначных чисел?
Подсказка 2
Как 20(a+b+c)+2(a+b+c) = 22(a+b+c)! Откуда a+b+c = 462/22 = 21. Осталось найти все наборы различных цифр, у которых сумма = 21)
Обозначим три различные цифры как Всевозможные двузначные числа:
По условию
Приведем общие слагаемые
То есть Так как это различные цифры,
Следовательно
Переберем возможные значения
Если то
Это возможно только в случае
и наоборот.
Если то
Это возможно только в случае
и наоборот.
Если то
Это возможно только в случае
и наоборот.
В случаях, когда или
перебирая всевозможные подходящие пары цифр
получаем уже найденные ранее
тройки.
Ошибка.
Попробуйте повторить позже
Существуют ли целые числа удовлетворяющие равенству:
Источники:
Подсказка 1
Что можно сказать про число 2023? Четное ли оно?
Подсказка 2
Да, 2023 - нечетное! А что можно сказать про три множителя в левой части уравнения? Какую четность они имеют?
Подсказка 3
Верно, поскольку чисел 3(x, y, z). То среди них будут либо 2 четных, либо 2 нечетных! А что мы знаем про сумму чисел одной четности? Каким по четности будет произведение трёх этих множителей?
Если бы такие три числа существовали, по крайней мере два из них имели бы одинаковую четность. Предположим, что это пара
чисел
и
. Тогда сумма
четная, а значит, четным должно быть и произведение
Число же
которому
это произведение должно равняться, — нечетное. Полученное противоречие показывает, что целых чисел, удовлетворяющих условию, не
существует.
Ошибка.
Попробуйте повторить позже
Можно ли найти четыре различных натуральных числа, каждое из которых не делится ни на ни на
ни на
но сумма любых двух
делится на
сумма любых трёх делится на
а сумма всех четырёх делится на
Источники:
Подсказка 1
Такс, наши числа не делятся на 2, 3 и 4, но при этом в сумме несколько чисел делятся на 2, 3 и 4. Что можно сказать про остатки при делении на 2, 3 и 4?
Подсказка 2
Верно, у всех чисел должны быть одинаковые остатки при делении на 2, 3 и 4! Ведь, в противном случае, найдется такой набор(например по модулю 3), что его сумма не будет делиться на 3. Осталось подобрать пример)
Подсказка 3
Для того, чтобы подобрать пример, давайте решим какие остатки будут давать наши числа при делении на каждое из чисел. Пусть эти остатки будут равны 1. Какие числа дают остаток 1 при делении на 3 и 4?(какой вид они имеют)
Подсказка 4
Верно, числа вида: 12k+1
Можно, например,
Указанные четыре числа можно записать в виде , где
принимает значения
поэтому сумма любых трёх
чисел
делится на Все числа в наборе нечётные, значит, сумма любых двух делится на
Наконец, сумма всех четырёх чисел равна
и
делится на
Ошибка.
Попробуйте повторить позже
Про различные положительные числа и
известно, что
Во сколько раз большее число превосходит меньшее?
Источники:
Подсказка 1
Если перефразировать условие, то нас просто просят найти отношение a к b. Подумайте, как можно свести данное нам уравнение к уравнение, в котором мы ищем a/b.
Подсказка 2
Давайте перенесем всё в одну сторону, приведем подобные и разделим на b³. Какое уравнение мы получим и как его проще всего решить?
Подсказка 3
Давайте сделаем замену a/b = x. Тогда мы получаем кубическое уравнение x³-6x²+9x-4=0. Внимательно посмотрите на коэффициенты в уравнении, на что они нам намекают?
Подсказка 4
Если сумма коэффициентов уравнения равна нулю, это значит, что единица является корнем данного уравнения. Но в условии сказано, что a не равно b, значит этот корень нам не подходит. Давайте вынесем из нашего уравнения множитель (x-1). Получили квадратное уравнение, решите его и найдите нужное нам отношение.
Рассмотрим и преобразуем разность:
По условию тогда получаем
значит большое число в
раза больше.
Ошибка.
Попробуйте повторить позже
Доход студента складывается из трёх источников: стипендия, временная подработка и помощь родителей. Если правительство удвоит
стипендию, то его доход возрастёт на Если время подработки увеличить в два раза, то доход возрастёт на
На сколько процентов
возрастёт доход студента, если его папа с мамой будут присылать денег вдвое больше?
Источники:
Подсказка 1
Обозначим каждый доход своей буквой, например: общий доход студента - S, стипендия - a, подработка - b, помощь родителей - c. Тогда верно равенство: S = a + b + c. А можно ли из оставшихся условий найти a и b?
Подсказка 2
Да, ведь 2a+b+c=1, 05S, тогда a = 1,05S-S=0,05S. Аналогично, b будет равно 0,15S. Что остаётся сделать, чтобы найти c?
Подсказка 3
Верно, надо подставить a и b в том виде, который мы получили на предыдущем шаге!
Пусть — ежемесячный доход студента,
и
— величины стипендии, подработки и помощи родителей соответственно (выраженные,
например, в рублях). Ясно, что
Тогда по условию
и
Из первого уравнения
из второго
тогда
то есть, доход студента возрастёт на
Ошибка.
Попробуйте повторить позже
Докажите, что для любых натуральных и
число
является составным.
Источники:
Подсказка 1
Такс, число точно будет не простым, если мы разложим наше число на несколько скобок так, что хотя бы 2 из них будут больше единицы! Попробуем сделать это.
Подсказка 2
Заметим, что 2022=6*337; 349=337+12; 72=6*12. Тогда остается вынести общий множитель нескольких слагаемых за скобки.
Подсказка 3
Да, мы получили две скобки: (6x+1)(337x+12y+2). При подстановке любых натуральных x и y каждая из скобок больше единицы, поэтому мы победили!
Попробуем разложить наше выражение на скобочки. Если каждая из них будет больше то мы победили!
Так как и
натуральные, то обе скобки больше
Следовательно, число — составное.
Ошибка.
Попробуйте повторить позже
Числа и
удовлетворяют равенствам
Какие значения может принимать сумма
Источники:
Подсказка 1
Подумайте, на что нам намекают выражения -(x+y+z), xy+yz+zx, -xyz.
Подсказка 2
По теореме Виета для кубического уравнения эти три выражения являются коэффициентами при t^2, t и свободным членом соответственно, при условии, что коэффициент при t^3 равен 1 и x, y, z являются корнями данного уравнения. Запишите такое уравнение и подумайте над значениями его корней.
Подсказка 3
Заметим, что сумма коэффициентов такого уравнения равна 0. А значит, 1 является корнем уравнения. Подставив 1 в условие вместо одного из неизвестных, получим, что оставшиеся два противоположны по знаку. Тогда чему равна сумма кубов этих трех чисел?
Пусть Тогда из условия
тоже равно
Значит, по теореме Виета числа
и
— это корни многочлена
Но число
является корнем такого многочлена, поэтому одно из чисел равно
Тогда два других числа
противоположны, а сумма кубов всех трёх равна
Ошибка.
Попробуйте повторить позже
Числа и
удовлетворяют равенству:
Найдите наибольшее значение выражения Ответ обоснуйте.
Источники:
Подсказка 1
Видим корни - пишем ограничения, возможно, они уже как-то приблизят нас к ответу.
Подсказка 2
Получили 0 ≤ x ≤ 1, 0 ≤ y ≤ 1. Если оценивать грубо, без оглядки на уравнение, то можно сказать, что x + 7y ≤ 8, но почти очевидно, что это не будет ответом, так что давайте поработаем над уравнением. У нас тут куча корней да еще и две переменных, кроме разложения на множители, пожалуй, тут ничего и не придумаешь. Подуйте, как здесь это лучше всего сделать.
Подсказка 3
Давайте из первого и третьего слагаемого вынесем √(7x), а из второго и четвертого -√(1-x). Как тогда будет выглядеть наше уравнения после вынесения разложения на множители?
Подсказка 4
Мы получаем два множители, один из которых зависит от x, а второй от y, а их произведение равно нулю. Мы знаем, что произведение двух множителей равно нулю, когда хотя бы один из множителей равен нулю. Таким образом мы получаем два случая. Рассмотрите оба и найдите максимально значение x+7y для каждого.
Проведём равносильные преобразования:
Тогда наибольшее значение выражения равно
Ошибка.
Попробуйте повторить позже
В произведении трёх натуральных чисел каждый сомножитель уменьшили на Могло ли произведение при этом увеличиться ровно на
Источники:
Подсказка 1
Сомножители уменьшили, а произведение при этом увеличилось, подумайте, как такое возможно?
Подсказка 2
Такое возможно только, если после уменьшения на 3, двое из сомножителей стали отрицательными. Какие значения могли иметь эти два множителя?
Подсказка 3
Если числа были натуральными, а после уменьшения на 3 стали отрицательными, то это значит, что каждый из сомножителей был равен 2 или 1. Какие значения из этих двух могли принимать множители?
Подсказка 4
Если оба равнялись 2, то произведение только уменьшилось бы. Если один равнялся 1, а второй - 2, то произведение стало бы меньше из-за уменьшения третьего множителя. Значит, оба множителя равнялись одному. Тогда какое значения принимал третий множитель?
В качестве примера подходит произведение После указанной операции получается
Как его можно придумать? Предположим, что два из сомножителей равнялись а третий —
Их произведение было равно
а
после уменьшения превратилось в
Значит, при
условие соблюдается. Решая это уравнение,
получаем
Ошибка.
Попробуйте повторить позже
Несколько восьмиклассников решали задачи. Учитель не записал у себя в журнале, сколько всего было учеников, и сколько задач каждый из них решил. Зато, он помнит, что, с одной стороны, каждый ученик решил задач больше, чем пятая часть от того, что решили остальные. А с другой стороны, он знает, что каждый ученик решил задач меньше, чем треть от того, что решили остальные. Сколько могло быть восьмиклассников? Найдите все варианты и докажите, что других нет.
Источники:
Подсказка 1
Как мы знаем (или не знаем) залог успешного решения задачи- удобно переписать условие. Давайте обозначим за n- количество учеников, за a(i)- количество решенных задач i-ого ученика и S=a(1)+a(2)+...+a(n). Как выглядит условие задачи в этих обозначениях?
Подсказка 2
Для любого номера i от 1 до n выполнены неравенства: (S-a(i))/5<a(i)<(S-a(i))/3. Это равносильно тому, что S/6<a(i)<S/4. Нас не сильно интересуют сами значения a(i), ведь нам нужно найти n. Что можно сделать с этими двойными неравенствами (их n штук), чтобы a(i) исчезли?
Подсказка 3
Конечно, сложить! Тогда мы получим двойное неравенство: nS/6<S<nS/4. Поделив все на S, получим, что n/6<1<n/4. Произошла магия и осталось только условие на n. Я верю, что вы справитесь и найдете все n, которые удовлетворяют этим неравенствам!
Пусть восьмиклассников было Пусть, кроме этого,
-й восьмиклассник (
) решил
задач. По условию для любого
выполнены неравенства
и
где
— общее количество решённых задач,
причём каждая задача учтена столько раз, сколько восьмиклассников её решили. Неравенства равносильны системе двойных
неравенств
Сложив почленно все эти неравенства, получим
что после сокращения на равносильно условию
Так как
— число целое, то
Ситуация с
возможна,
например, если все ученики решили по
задаче.
Ошибка.
Попробуйте повторить позже
Можно ли по окружности расставить черных и несколько белых фишек так, чтобы каждой черной фишке соответствовала
диаметрально противоположная белая фишка и никакие две белые не стояли рядом?
Подсказка 1
Давайте задавать себе правильные, наводящие вопросы. Для начала мы ничего не знаем про количество белых фишек. Попробуем это исправить. По условию никакие две белые фишки не стоят рядом, а диаметрально противоположные различных цветов. Учитывая, что фишек у нас всего двух цветов, какой вывод из этого можно сделать?
Подсказка 2
Верно, делаем вывод, что чёрные фишки тоже чередуются, а белых фишек столько же, как и чёрных, - 2n штук. Давайте предположим, что у нас получилось расставить фишки по окружности. Теперь попробуем воспользоваться ещё вторым условием задачи.
Подсказка 3
Посмотрим на две произвольные фишки на диаметре. Что тогда можно сказать о количестве фишек между ними, и не будет ли там противоречия?
Подсказка 4
Ага, фишек между ними будет (4n - 2)/2 = 2n - 1. Это нечётное число, а у нас фишки одинаковых цветов не стоят рядом.
Подсказка 5
Получаем противоречие, так как крайние фишки среди 2n-1 будут одноцветные., а должны чередоваться Победа!
Так как каждой черной фишке соответствует диаметрально противоположная белая фишка и никакие две белые не стоят рядом, то фишки
должны чередоваться, и значит, белых фишек тоже Получается, что всего фишек
а на полуокружности между
черной и белой фишкой стоит
фишка, поэтому крайние из них одноцветны, следовательно, расстановка
невозможна.
Ошибка.
Попробуйте повторить позже
Вася придумал новый корабль для морского боя — “боевой бублик”. Этот корабль состоит из всех клеток квадрата , кроме его
центральной клетки. На поле
разместили один боевой бублик. Какое минимальное число выстрелов нужно сделать, чтобы
гарантированно его ранить?
Подсказка 1
Попробуем найти маленькую фигуру, в которой нам точно не хватит одного выстрела.
Заметим, что если бублик размещен на поле , то одного выстрела не хватит, чтобы гарантированно его ранить. Действительно, если
выстрел произведен в клетку, соседнюю со стороной квадрата, то бублик может быть размещен рядом с противоположной стороной. Если же
выстрел произведен в одну из четырех центральных клеток квадрата, то бублик может быть размещен так, что его центр совпадает
с клеткой, в которую сделан выстрел. Значит, потребуется сделать не менее двух выстрелов, чтобы гарантированно его
ранить.
Разбив поле на четыре квадрата
, получим, что для того, чтобы гарантированно ранить бублик, потребуется не менее 8
выстрелов.
Если же сделать 8 выстрелов так, как показано на рисунке, то мы гарантированно раним бублик.
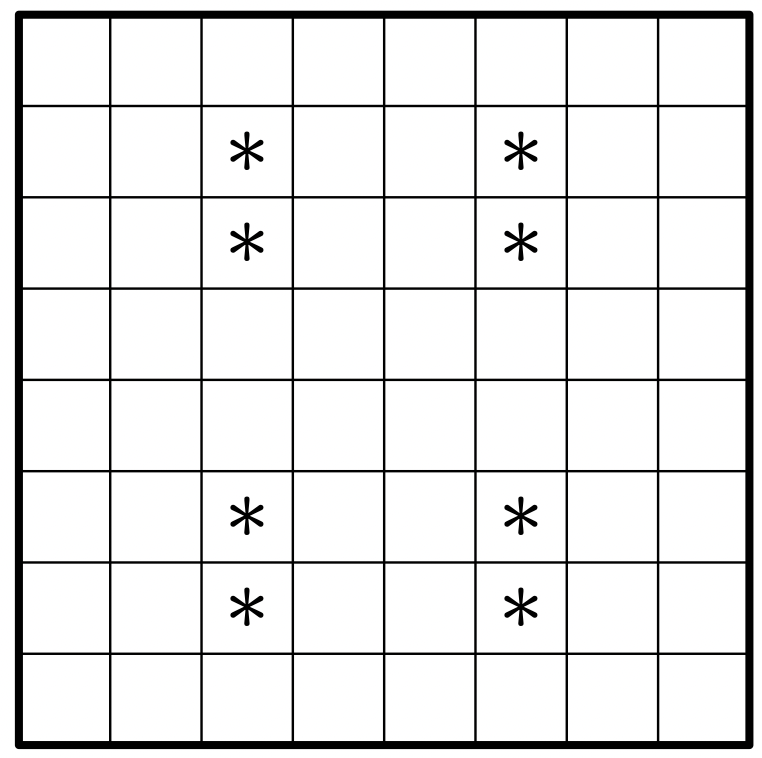
Ошибка.
Попробуйте повторить позже
На шахматную доску поставили
ладей и
коней так, что ни одна из фигур не бьёт никакую другую. При каком наибольшем
такое возможно?
Подсказка 1
Одна ладья, которую мы ставим на доску забирает сразу 15 клеток! Попробуйте придумать оценку через этот факт
Подсказка 2
Верно, для любой расстановки хотя бы 6 ладей, свободными останутся не более 4 клеток, поэтому ладей не больше 5! Это так, поскольку 6 ладей занимают не менее 6*15 - 2 - 4 - 6 - 8 - 10 = 60 клеток
Подсказка 3
Остаётся придумать пример расстановки 5 ладей и 5 коней
Все ладьи должны стоять на разных столбцах и строчках. Тогда при остаётся не более 4 небитых клеток для коней, и 6 коней уже не
расставить.
Пример при на рисунке.
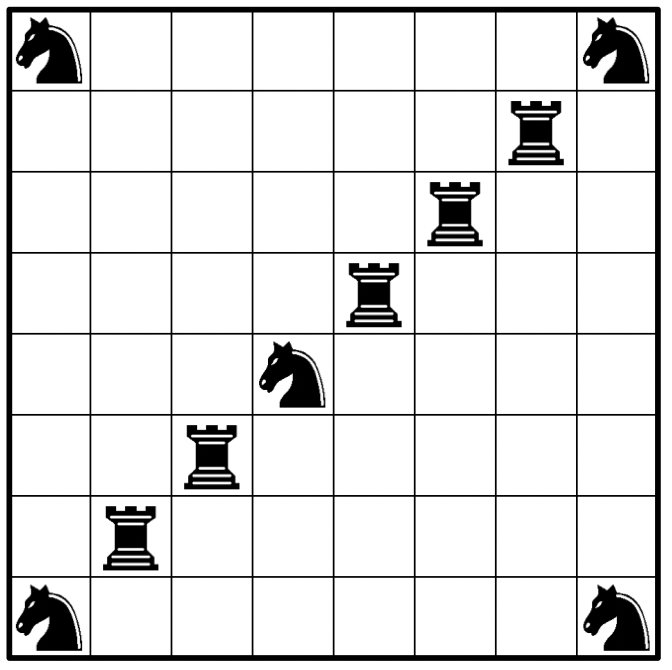
Ошибка.
Попробуйте повторить позже
В каждой из трёх коробок лежит по 2016 спичек. Двое играющих берут по очереди любое число спичек из любой коробки, но только из одной. Выигрывает тот, кто берёт последнюю спичку. Докажите, что тот, кто ходит первым, может выиграть, как бы ни играл его партнер.
Подсказка 1
Попробуем воспользоваться идеей симметрии, но у нас три коробки, а хотелось бы 2… Что будет, если первый игрок избавиться от одной из коробок первым же ходом?
Подсказка 2
Да, тогда у нас будет две коробки, что в таком случае хочется делать за первого игрока, после каждого хода второго(вспомните про симметрию)
Подсказка 3
Верно, первый игрок может делать точно такие же ходы, как и второй, но уже в другой коробке!
Первым ходом начинающий должен забрать все спички из любой коробки. После этого останутся две коробки, и ему надо в дальнейшем каждым своим ходом брать столько же спичек, сколько взял перед этим его партнер, но из другой коробки. Придерживаясь такой стратегии, первый будет каждым своим ходом уравнивать число спичек в коробках и ясно, он рано или поздно выиграет.
Ошибка.
Попробуйте повторить позже
В треугольнике медиана
в два раза меньше стороны
и образует с ней угол
Найдите градусную меру угла
.
Подсказка 1
Так, у нас есть условие про медиану. Тогда что самое первое можно сделать в задаче?
Продлим медиану за точку
на ее длину и получим точку
.
![]()
Так как , получаем, что
, т.е. треугольник
равнобедренный. Следовательно,
Четырехугольник является параллелограммом, так как его диагонали точкой пересечения делятся пополам.
Значит,
Тогда
Ошибка.
Попробуйте повторить позже
и
— биссектрисы треугольника
Длины перпендикуляров, опущенных из вершины
на прямые
и
равны.
Докажите, что треугольник
равнобедренный.
Подсказка 1
Давайте обозначим основание перпендикуляров X и Y. И естественно провести третью биссектрису. Когда есть перпендикуляры, то есть и прямоугольные треугольники. Тогда какая деталь первая бросается в глаза на картинке, зная, что перпендикуляры равны?
Подсказка 2
Верно, можно увидеть равенство прямоугольных треугольников XIN и YIN, где I — точка пересечения биссектрис. Но нам нужна равнобедренность, и один из способов это доказать через углы. Какие же ещё для этого можно увидеть равные треугольники на картинке?
Подсказка 3
Ага, это треугольники NIM и NIP, равные по стороне и двум углам. Но тогда и третий уголок у них равный, а из-за биссектрисы получаем требуемое в задаче. Победа!
Первое решение.
![]()
Пусть и
перпендикуляры, опущенные из вершины
на прямые
и
Продолжим перпендикуляры
и
до пересечения с прямой
(точки пересечения соответственно
и
). Треугольники
и
равнобедренные (биссектрисы
и
являются высотами), отсюда
,
и
. Из последнего равенства
.
Тогда треугольники
и
равны. Следовательно,
Второе решение.
![]()
Пусть — точка пересечения биссектрис треугольника
Из равенства прямоугольных треугольников
и
с общей
гипотенузой следует, что
Отсюда с учетом равенств
и
следует, что
, т.е.
.
Ошибка.
Попробуйте повторить позже
В равнобедренном прямоугольном треугольнике угол
равен
, точка
середина
Прямая, проходящая через точку
и перпендикулярная
, пересекает сторону
в точке
. Докажите, что
.
Подсказка 1
Нам дали в задаче хорошую фигуру, но давайте её ещё "улучшим", чтобы связать отрезки на картинке или получить более удобную конструкцию. Тогда до какой фигуры логично достроить нашу картинку?
Подсказка 2
Да, конечно же до квадрата, и, чтобы точно на картинке всё было связано, продлим AP до пересечения со стороной квадрата в точке N. У нас достаточно много прямых уголков образовалось, четырёхугольников и прямоугольных треугольников. Нельзя ли что-то понять про один из четырёхугольников?
Подсказка 3
Верно, один из них является вписанным, а значит углы AMC и ABN равны. Тогда, если эти два угла равны PMB, то становится понятно, что же нам в итоге надо доказать. Равенство треугольников PMB и PNB. Получается для этого нам не хватает только равенства MB и BN. Как это можно доказать? Может быть стоит воспользоваться какими-то двумя другими треугольниками для этого.
Подсказка 4
Верно, можно сказать, что треугольники ACM и ABN равны по катету(стороне квадрата) и острому углу. Откуда и получаем равенство сторон, а значит, как мы поняли до этого, решаем задачу. Победа!
Достроим равнобедренный прямоугольный треугольник до квадрата
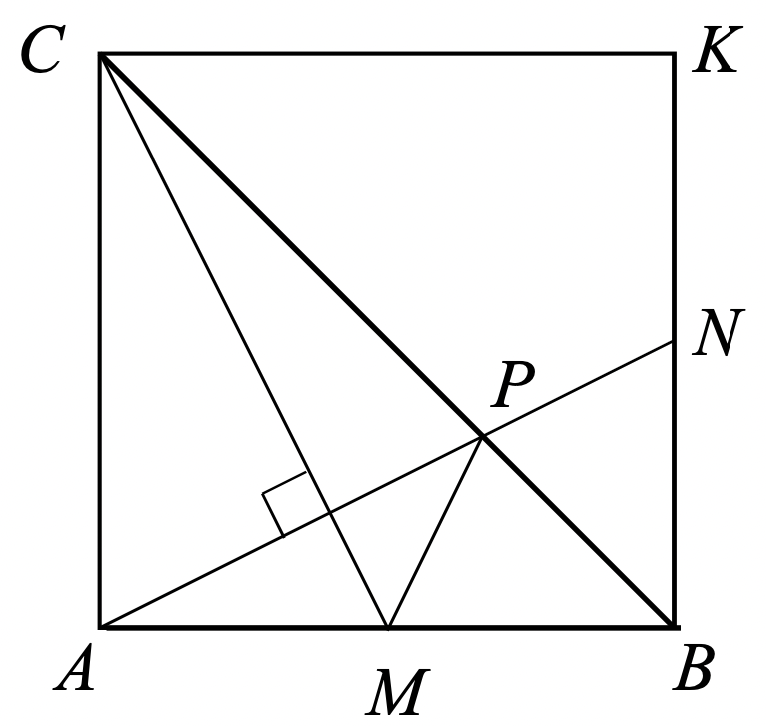
Пусть — точка пересечения
и
Прямые
и
взаимно перпендикулярны, поэтому
Отсюда
следует равенство прямоугольных треугольников
и
, и значит,
Так как
и
, то
треугольники
и
равны по двум сторонам и углу между ними. Следовательно,
и так как
, требуемое равенство доказано.



