Муниципалка 10 - 11 класс —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Муниципалка 10 - 11 класс

Тема Муниципальный этап ВсОШ

Муниципалка 10 - 11 класс

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела муниципальный этап всош

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#72245

В треугольнике $ABC$ синус угла $A$ равен $3∕5.$ На стороне $AC$ взяли точку $M$ так, что $CM =15,$ на стороне $AB$ взяли точку $N$ так, что $BN = 7,AN = AM,$ $T$ — середина $NC,$ $P$ — середина $BM.$ Найдите длину отрезка $P T.$

Источники: Муницип - 2022, Республика Башкортостан, 10.4

Подсказки к задаче

Подсказка 1

У нас отмечены две середины, может, стоит поискать средние линии? Попробуйте придумать какую-нибудь среднюю линию с точкой T...

Подсказка 2

Можно взять точку L- середину BC. Тогда TL- средняя линия треугольника △NCB ⇒ TL=7/2 и TL // AB. А что мы можем сказать про PL?

Подсказка 3

Это тоже средняя линия, только для треугольника △MBC ⇒PL=15/2 и PL // AC. Из параллельности следует, что уголок ∠PLT равен ∠BAC. Можем ли мы уже найти PT?

Подсказка 4

Конечно можем, ведь у нас есть теорема косинусов! Доведите решение до конца и не забудьте, что cos(∠BAC) может принимать два значения...

Показать ответ и решение

$PIC$

Обозначим длины $AN$ и $AM$ за $x.$ Введём систему из двух единичных векторов: пусть вектор $−→ b$ коллинеарен вектору $−→ AB,$ а вектор $−→c$ коллинеарен вектору $−A→C.$ Тогда верны векторные соотношения:

−→PT =−A→T − −→AP,−A→P = 1(−A→B + −−A→M ),−A→T = 1(−→AC+ −−A→N ) 2 2 −→AB = (x+ 7)⃗b,−→AC = (x+ 15)⃗c, −A−→M = x⃗c, −A−→N = x⃗b −→ 1 −→ −−→ −→ −−→ 1 ⃗ P T = 2(AC +AN − AB −AM )= 2(15⃗c− 7b)

Вычисляя скалярный квадрат вектора $−→ PT,$ и учитывая, что косинус угла $\text{[math]}$ может быть равен равен $4∕5$ для острого угла и $− 4∕5$ для тупого, получим

−→ −→ 1 PT ⋅PT = 4(49⃗b⋅⃗b+225⃗c⋅⃗c− 210⃗b⋅⃗c)= 26,5 −→ −→ 1 ⃗⃗ ⃗ PT ⋅PT = 4(49b⋅b+225⃗c⋅⃗c− 210b⋅⃗c)= 110,5

Ответ:

$√26,5;√110,5$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#72244

В треугольнике $ABC$ на стороне $BC$ отмечены точки $A 1$ и $A 2$ ( $A 1$ лежит между $B$ и $A 2$ ) так, что $∠BAA = ∠A AA =∠A AC, 1 1 2 2$ а на стороне $AC$ — точки $B1$ и $B2$ ( $B1$ лежит между $A$ и $B2$ ) так, что $∠ABB1 =∠B1BB2 = ∠B2BC.$ Оказалось, что как прямые $AA1$ и $BB1,$ так и прямые $AA2$ и $BB2$ пересекаются на биссектрисе угла $C.$ Докажите, что треугольник $ABC$ — равнобедренный.

Источники: Муницип - 2022, Кировская область, 10.4

Подсказки к задаче

Подсказка 1

Пускай AA₂ и BB₂ пересекаются в точке O₂, а AA₁ и BB₁ в точке O₁. Какой точкой является O₁ для треугольника AO₂B?

Подсказка 2

Т.к. AO₁ и BO₁- это биссектрисы углов ∠O₂AB и ∠O₂BA ⇒ O₁- точка пересечения биссектрис ⇒ O₂O₁- биссектриса. Что тогда можно сказать про треугольники △CB₂O₂ и △CA₂O₂?

Подсказка 3

Верно, они равны по стороне и двум углам! Но тогда уголки ∠AB₂B и ∠AA₂B равны ⇒ AB₂A₂B- вписанный. Поймите, каким является четырехугольник AB₂A₂B, если вспомнить, что O₂B₂=O₂A₂, и завершите решение!

Показать доказательство

Пусть прямые $AA 1$ и $BB 1$ пересекаются в точке $O , 1$ прямые $AA 2$ и $BB 2$ — в точке $O , 2$ а $CD$ — биссектриса треугольника $ABC.$ $O1$ — точка пересечения биссектрис треугольника $ABO2,$ поэтому $O2D$ — биссектриса этого треугольника.

$PIC$

Отсюда

∠B2O2C = ∠BO2D = ∠AO2D =∠A2O2C

Кроме того, по условию $∠B2CO2 = ∠A2CO2.$ Поэтому

∠BA2O2 = ∠A2CO2+ ∠A2O2C = ∠B2CO2+ ∠B2O2C = ∠AB2O2

Положим $∠BAC = 3α,∠ABC = 3β.$ Тогда

180∘− 3α− 2β = ∠AB2O2 =∠BA2O2 = 180∘− 2α− 3β,

откуда $α =β.$

Ошибка.
Попробуйте повторить позже

Задача 3#72243

Окружность проходит через вершину В треугольника $ABC$ , пересекает стороны $AB$ и $BC$ в точках $X$ и $Y$ соответственно, и касается стороны $AC$ в ее середине $M.$ Известно, что $AX = XM.$ Докажите, что $CY = YM.$

Источники: Муницип - 2022, Костромская область, 10.3

Подсказки к задаче

Подсказка 1

Для начала стоит подумать, что нам может дать равенство AX=XM. Мы понимаем, что из него следует, что ∠BAC=∠XMA. Где мы еще можем найти уголочек ∠XMA (вспомните про касание окружности)?

Подсказка 2

Т.к. AM- касательная, то по теореме об угле между касательной и хордой: ∠XMA=∠XBM ⇒ △AMB- равнобедренный. А что мы можем сказать про треугольник △BMC?

Подсказка 3

Т.к. M- середина AC ⇒ MB=MA=MC ⇒ ∠MBC=∠BCM. Вспомните, мы доказали похожее равенство, используя то, что XM=AX. Попробуйте повторить те же рассуждения в обратном порядке и доказать, что YM=CY.

Показать доказательство

$PIC$

Из равнобедренного треугольника $AXM$ : $∠XAM =∠AMX, ∠AMX = ∠XBM$ (угол между хордой и касательной равен вписанному углу, опирающемуся на эту хорду).

Тогда в треугольнике $AMB$ : $∠BAM = ∠ABM,$ значит $MC = AM = BM.$

В треугольнике $CMB$ : $MC = MB,$ значит $∠MBC =∠MCB, ∠Y MC = ∠MBY$ (угол между хордой и касательной равен вписанному углу, опирающемуся на эту хорду).

Получаем, что $∠YMC =∠Y CM,$ откуда $CY = YM.$

Ошибка.
Попробуйте повторить позже

Задача 4#72242

В остроугольном неравнобедренном треугольнике $ABC$ проведены высоты $AA 1$ и $CC , 1$ и отмечены точки $K,$ $L$ и $M$ — середины сторон $AB,$ $BC$ и $CA$ соответственно. Докажите, что если $∠C1MA1 =∠ABC,$ то $C1K = A1L.$

Источники: Муницип - 2022, Орловская область, 10.3

Подсказки к задаче

Подсказка 1

Давайте для начала подумаем, что нам дает равенство уголочков ∠ABC и ∠A₁MC₁. Мы знаем, что сумма уголков ∠C₁MA+∠C₁MA₁+∠A₁MC=180°. Как нам выразить ∠C₁MA и ∠A₁MC через углы треугольника ∠ABC?

Подсказка 2

Т.к. △AMC₁ и △CMA₁- равнобедренные, то ∠AMC₁=180°-2∠BAC, ∠CMA₁=180°-2∠BCA ⇒ ∠ABC=2(180°-∠ABC)-180° ⇒ ∠ABC=60°. Тогда очень интересным выглядит треугольник △BC₁C. Что можно сказать про сторону BC₁?

Подсказка 3

Верно, она равна BC/2. Но мы знаем, что BL=BC/2 ⇒ BC₁=BL. Из аналогичных рассуждений можно получить, что BK=BA₁. Как тогда завершить решение?

Подсказка 4

Посмотрите на равенство BC₁-BK=BL-BA₁!

Показать доказательство

$PIC$

Давайте сначала узнаем, для чего же нам дали равенство углов. Пусть $∠ABC = β,∠ACB = γ,∠BAC =α.$ Тогда можем выразить угол $C1MA1$ через два других угла треугольника. Понятно, что $AM = CM =C1M = A1M.$ Тогда

∠AMC1 =180∘− 2α ∠CMA1 = 180∘− 2β

∠C1MA1 = β = 180∘− (180∘− 2α)− (180∘ − 2β)= 2(α +β)− 180∘

Но мы знаем, что $∘ α +β +γ =180 .$ Тогда

β =2(180∘− β)− 180∘

∘ β = 60

Отлично! Значит, на самом деле нам дали треугольник с углом $60∘.$ Но тогда $KL = C1A1 = AC2 ,$ так как $KL$ — это средняя линия треугольника, а $△A BC 1 1$ подобен исходному с коэффициентом $cos60∘,$ откуда и получаем равенство. Теперь видим, что если докажем равенство треугольников $KC1L$ и $A1C1L,$ то мы победим! Одна пара сторон у них равные, а $C1L$ общая сторона. Давайте найдём угол между ними. Будем использовать знания о том, что $ACA1C1$ вписанный, $KL$ параллельно $AC$ и из прямоугольного треугольника $BC1 = BL= C1L.$ Тогда

∠KLC1 = ∠C1LB − ∠KLB = ∠LC1B− ∠A1C1B = ∠LC1A1

Значит, треугольники $KC1L$ и $A1C1L$ равны по двум сторонам и углу между ними. Тогда и $KC1 = A1L.$ Победа!

Ошибка.
Попробуйте повторить позже

Задача 5#72241

Сторона $AB$ треугольника $ABC$ больше стороны $BC,$ а угол $B$ равен $40∘.$ На стороне $AB$ взята точка $P$ так, что $BP = BC.$ Биссектриса $BM$ пересекает описанную около треугольника $ABC$ окружность в точке $T.$ Найдите градусную меру угла $MP T.$ В ответ внесите число градусов.

Источники: Муницип - 2022, Республика Татарстан, 10.5

Подсказки к задаче

Подсказка 1

Давайте сначала подумаем, как уголочек ∠MPT связан с картинкой. Вроде как, его нет в каких-то хороших треугольниках. Тогда посмотрим на четырехугольники: в глаза бросается четырехугольник APMT. Что бы мы хотели про него понять, чтобы приблизиться к решению?

Подсказка 2

Хотелось бы, конечно, доказать, что он вписанный. Для этого можно, например, доказать, что ∠ATM+∠APM=180°. Уголочек ∠ATM можно легко перекинуть на ∠ACB. А что делать с ∠APM?

Подсказка 3

Мы видим, что ∠APM- внешний для треугольника △BPM. Какому треугольнику равен △BPM?

Подсказка 4

Конечно, △BCM! Отсюда все и следует. Тогда: APMT- вписанный ⇒ ∠MPT=∠MAT. Найдите уголок ∠MAT и радуйтесь жизни!

Показать ответ и решение

В четырехугольнике $APMT$ угол при вершине $A$ измеряется половиной дуги $TCB.$ Треугольники $P MB$ и $CMB$ равны по двум сторонам и углу между ними, поэтому $∠PMB =∠CMB = ∠AMT.$ Угол $AMT$ измеряется полусуммой дуг $AT$ и $CB,$ причём:

1 1 1 2(⌣ AT +⌣ CB )= 2(⌣ TC+ ⌣ CB) =2 ⌣ TCB

$PIC$

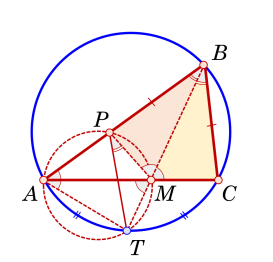
Значит, $∠CMB =∠BAT.$ Таким образом, $∠P MB = ∠BAT$ и

∠BAT +∠PMT = ∠BAT +(180∘ − ∠P MB )=180∘

Следовательно, сумма противоположных углов четырехугольника $APMT$ равна $180∘,$ и значит, $APMT$ — вписанный. По свойству вписанных углов

∠MP T = ∠MAT = ∠CAT =∠T BC = 1∠ABC = 20∘ 2

Ответ: 20

Ошибка.
Попробуйте повторить позже

Задача 6#72181

Даны $n$ различных положительных чисел. Из них составляются суммы с любым числом слагаемых от $1$ до $n.$

(a) Какое наименьшее количество различных сумм можно получить?

(b) Какое наибольшее количество различных сумм можно получить?

Источники: Муницип - 2021, Татарстан, 11.5

Подсказки к задаче

Пункт a), подсказка 1

Давайте упорядочим наши числа! Тогда можно составить достаточное количество таких наборов чисел, что между любыми двумя наборами мы сможем точно поставить знак больше или меньше. Попробуем построить такой набор!

Пункт a), подсказка 2

Такс, очевидно, так как мы упорядочили наши числа, то мы можем сказать, что первое меньше второго, второе меньше третьего и так далее. А если к каждому из чисел(кроме последнего) прибавить максимальное число? Что можно сказать про такой набор чисел, каждое из которых состоит из двух слагаемых?

Пункт a), подсказка 3

Верно, эти числа тоже будут идти по возрастанию! То есть, знаки в таком наборе будут полностью совпадать со знаками в первом наборе, поэтому он тоже будет возрастающим(но в нём не будет последнего числа). Аналогично, дальше мы можем прибавлять максимум из оставшихся чисел к каждому числу из набора и тем самым получать новый набор! Сколько всего чисел тогда будет, если в первом наборе n, во втором n-1, в третьем n-2..,?

Пункт a), подсказка 4

Да, всего чисел будет n*(n-1)/2. Остаётся привести пример, когда все другие суммы, которые мы не рассматривали будут совпадать с хотя бы одним из рассмотренных нами чисел(для этого стоит располагать все n чисел компактно по отношению друг к другу)

Пункт b), подсказка 1

Представим, что все-все суммы будут различны. Как тогда удобно представлять каждую из сумм?

Пункт b), подсказка 2

Верно, тогда удобно считать, что каждое из чисел либо есть в сумме, либо его нет! То есть, на каждое число существует 2 варианта! Сколько всего вариантов, в таком случае?

Пункт b), подсказка 3

Да, таких сумм всего 2ⁿ - 1. Вычитаем единицу, потому что невозможен вариант, когда мы не взяли в сумму ни одного числа. Остается привести пример, когда такое возможно, для этого попробуйте взять числа на достаточно большом расстоянии друг от друга или чтобы каждое из чисел влияло только на одну цифру в сумме!

Показать ответ и решение

Можно считать, что исходные положительные числа расположены в порядке возрастания: $a < a < ...< a. 1 2 n$ Рассмотрим

$PIC$

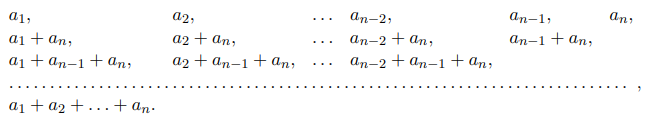
Очевидно, что здесь каждое число больше предыдущего, поэтому все выписанные числа различны. Их количество $n +(n− 1)+...+ 1= 12n(n+ 1)$ соответствует требованиям задачи.

Осталось привести пример, в котором больше, чем $12n(n+ 1)$ различных сумм получить не удастся. Для этого подойдет набор из первых $n$ натуральных чисел, из которых нельзя составить больше, чем $12n(n +1)$ различных сумм: эти суммы - все натуральные числа от $1$ до $1+ 2+ ...+ +n= 12n(n+ 1).$

б) Каждое число $ai$ входит или не входит в рассматриваемую сумму. Кроме того, нужно ещё исключить сумму, не содержащую ни одного слагаемого, поэтому различных сумм из $n$ слагаемых можно составить не более, чем $2n− 1.$

Числа $1,10,102,...,10n−1$ дают пример $n$ различных чисел, из которых можно образовать наибольшее число различных сумм. Сумма любых $k$ чисел этого набора - это число, в десятичной записи которого используются только $1$ и $0.$ Каждая такая сумма может быть представлена в виде $n$ -элементного упорядоченного набора из $0$ и $1.$ Поскольку на каждом месте набора могут быть только две цифры, их общее количество равно $2⋅2⋅...⋅2= 2n.$ Единственный невозможный набор, составленный из $n$ нулей, необходимо исключить, поэтому общее количество допустимых наборов равно $2n− 1.$

Ответ:

$a) n(n+1) 2$

$n b) 2 − 1$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#72179

Шахматный турнир прошёл по круговой системе, где каждый участник сыграл с каждым один раз. Назовём партию неправильной, если выигравший её шахматист в итоге набрал очков меньше, чем проигравший. (Победа даёт $1$ очко, ничья — $1∕2,$ поражение — $0$ ). Могут ли неправильные партии составлять более $75%$ от общего количества партий в турнире?

Источники: Муницип - 2021, Бурятия, 11.5

Подсказки к задаче

Подсказка 1

Введём для начала обозначения. Пусть всего игроков было N. И давайте выделим половину участников турнира, пусть M= [N/2]. Тогда первые M людей будут сильными, а остальные слабыми. Как теперь можно задачу в таком виде удобно для нас переформулировать?

Показать ответ и решение

Пусть $N$ — число игроков, $M = [N∕2].$

Игроков, занявших первые $M$ мест, назовём сильными, а остальных – слабыми (между участниками с одинаковой суммой очков места распределяются произвольно). Пусть $X$ — число правильных партий между сильными и слабыми.

Сумма очков, набранных сильными во встречах между собой, равна $M(M−1) 2 ,$ а во встречах со слабыми — не больше $X.$

Поэтому средний результат сильного не больше $M−-1 X- 2 + M.$ Аналогично, средний результат слабого не меньше $N−M-−1 M(N−M-)−X- 2 + N −M .$

Если есть неправильные партии, то не все игроки набрали поровну, и средний результат сильного больше, чем слабого. Отсюда

M (N − M ) N (N − 1) X >----2----≥ ---8---

Так как общее число партий равно $N(N2−1),$ доля правильных партий больше $1∕4,$ то есть более $25$ процентов.

Ответ: нет

Ошибка.
Попробуйте повторить позже

Задача 8#72173

В спортивной школе занимается $55$ человек, каждый из которых либо теннисист, либо шахматист. Известно, что нет четырёх шахматистов, которые имели бы поровну друзей среди теннисистов. Какое наибольшее количество шахматистов может заниматься в этой школе?

Источники: Муницип - 2021, Москва, 11.4

Подсказки к задаче

Подсказка 1

Обозначим количество шахматистов и теннисистов. Так как всего 55 человек, то если теннисистов ровно a, тогда шахматистов 55-a. Попробуем прийти к условию, надо понять в каком случае у четырех шахматистов не будет поровну друзей теннисистов. Для этого надо понять, сколько всего друзей теннисистов может быть у каждого шахматиста?

Подсказка 2

Верно, от 0 до a(то есть, любое число от 0 до общего числа теннисистов). Что должно выполняться, чтобы у четырех шахматистов не было поровну друзей теннисистов?

Подсказка 3

Да, по принципу Дирихле шахматистов должно быть не больше 3(a+1). А по нашим обозначениям, шахматистов ровно 55-a. Тогда имеет место неравенство: 55-a ≤ 3(a+1). Остаётся найти такое a, чтобы 55-a было максимально возможным и привести пример!

Показать ответ и решение

Пусть в школе занимаются $a$ теннисистов и $55− a$ шахматистов. У каждого из шахматистов количество друзей-теннисистов не меньше $0$ и не больше $a,$ то есть может принимать $a+ 1$ значений. Если бы шахматистов было больше $3(a +1),$ среди них по принципу Дирихле нашлись четверо с одинаковым количеством друзей-теннисистов. Значит, шахматистов не больше $3(a+1),$ получаем неравенство $55− a≤ 3(a+ 1).$ Решая его, получаем $a≥ 13,$ тогда $55− a ≤55− 13= 42.$

Заметим также, что ровно $42$ шахматиста могло быть: пусть для каждого целого $0≤ k≤ 13$ какие-то трое шахматистов имеют ровно $k$ произвольных друзей-теннисистов.

Ответ: 42

Ошибка.
Попробуйте повторить позже

Задача 9#68197

Точки $O$ и $I$ — центры описанной и вписанной окружностей соответственно для треугольника $ABC$ , $M$ — середина дуги $AC$ описанной окружности (не содержащей точки $B$ ). Известно, что $AB = 15,BC = 7$ и $MI = MO.$ Найдите $AC.$

Источники: Муницип - 2021, Татарстан, 11.3

Подсказки к задаче

Подсказка 1

У нас есть центр вписанной окружности и середина дуги, хочется использовать...

Подсказка 2

Лемму о трезубце! Получим, что MA=MI=MO. Но что из этого следует?

Подсказка 3

Треугольник AOM - равносторонний! Тогда можно найти угол AOM, а значит, и угол ABC, а дальше дело техники.

Показать ответ и решение

$PIC$

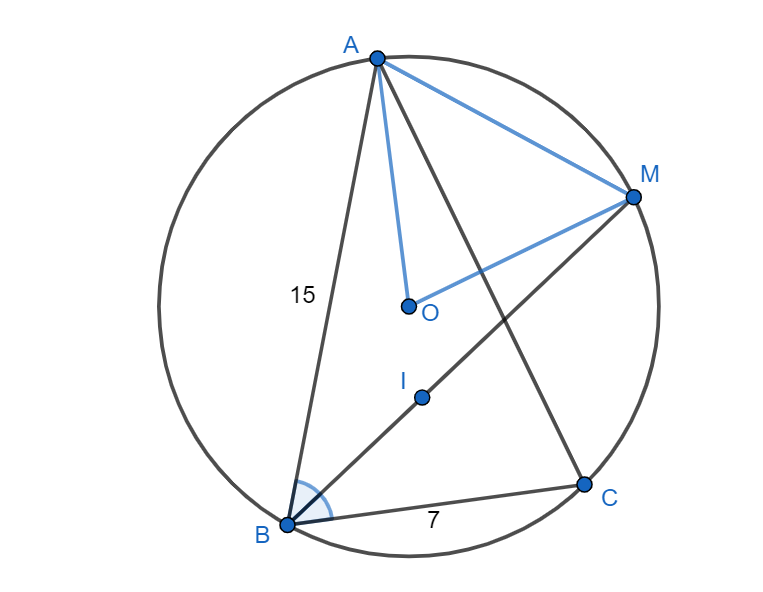
Середина дуги $M$ лежит на биссектрисе $BI.$

По лемме о трезубце $AM = MI =R$ (по условию $OM = R =MI$ ).

Отсюда

∠B = 60∘

По теореме косинусов

∘ ------------ AC = 152+72− 15⋅7= 13

Ответ: 13

Ошибка.
Попробуйте повторить позже

Задача 10#43951

Два игрока играют в следующую игру на доске $m × n$ клеток $(m, n> 1$ ). У них есть белый и чёрный король соответственно, стоящие в противоположных углах доски. Они передвигают своих королей (по правилам шахмат) поочередно так, чтобы расстояние между центрами клеток, на которых стоят короли, уменьшалось (королям разрешается занимать соседние клетки). Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

Подсказки к задаче

Подсказка 1

Давайте для удобства введем переменные x и y- разность координат королей. У нас в задаче происходит какой-то процесс, за которым трудно уследить. Может тогда стоит поискать какие-то выигрышные "позиции", в которые наши игроки могут приводить наших королей...

Подсказка 2

Предлагаю ввести три типа позиции (будем называть их проигрышными): 1) x=0, y- нечетный 2) y=0, x- нечетный 3) x, y≠0, x,y- четные. Для начала поймите, что за один ход из проигрышных нельзя прийти обратно в проигрышные...

Подсказка 3

Забыл сказать, что все остальные позиции мы называем выигрышными. Если мы докажем, что из любой выигрышной позиции мы можем перейти в проигрышную, то мы можем гарантировать сохранение выигрышной позиции после двух ходов. Как же это доказать?

Подсказка 4

На самом деле это почти очевидно, ведь мы можем x или y уменьшать на 1 независимо. Как тогда выглядит стратегия?

Подсказка 5

Как мы поняли, если изначально первый стоял на выигрышной позиции, то он сумеет ее сохранить до конца. Если же он стоял на проигрышной, то второй может оставлять его и дальше на проигрышной позиции. Поймите, почему в конце игры на проигрышной позиции игрок проигрывает, и подберите m и n, при которых первый игрок изначально будет стоять на проигрышной позиции.

Показать ответ и решение

Рассмотрим разность координат королей: обозначим их через $x$ и $y.$ Заметим, что вначале $x = m− 1,y = n− 1.$ Мы докажем, что в следующих позициях первый проигрывает, а во всех остальных выигрывает: a) $x= 0$ и $y$ нечетно; б) $y =0$ и $x$ нечетно; в) $x ⁄=0,y ⁄= 0,x$ и $y$ оба четны.

Во-первых, очевидно, что игрок не может из одной проигрышной позиции попасть в другую проигрышную позицию. Также необходимо показать, что из любой выигрышной позиции можно попасть в проигрышную. Нам необходимо рассмотреть два случая (без ограничения общности можно считать, что $x,y ≥ 0$ ):

1) $x,y ≥ 1$ — легко видеть, что правила позволяют уменьшать $x$ или $y$ на 1 независимо. Также очевидно, что мы можем или обе координаты сделать четными, или одну сделать нулем, а другую — нечетной;

2) $x= 0$ — мы просто уменьшаем $y$ на 1;

3) $y = 0$ — аналогично предыдущему уменьшаем $x$ на 1 .

Итак, если первый игрок находится в выигрышной позиции, он и далее всегда может оставаться в выигрышной позиции. Если же он стоит на проигрышной позиции, второй игрок не даст ему занять выигрышную позицию. Так как расстояние между королями уменьшается, игра закончится, и из последней проигрышной позиции не может быть сделано никакого хода.

Ответ:

Второй игрой выигрывает, если $m$ и $n$ оба нечетны. Во всех остальных случаях выигрывает первый.

Ошибка.
Попробуйте повторить позже

Задача 11#43950

Дана клетчатая таблица $101×101$ , клетки которой покрашены в белый цвет. Разрешается выбрать несколько строк и перекрасить все клетки этих строк в чёрный цвет. Затем выбрать ровно столько же столбцов и перекрасить все клетки этих столбцов в противоположный цвет (то есть белые — в чёрный, и чёрные — в белый). Какое наибольшее число чёрных клеток может содержать таблица после этой операции?

Подсказки к задаче

Подсказка 1

Следует сделать явное описание процесса(и ситуации в конце) по кол-ву черных клеток. Если, скажем, изначально было выбрано k строк для перекрашивания в черный цвет.

Подсказка 2

В силу того, что в каждой строке было k 101 черная клетка после изменения, а потом из них стало (в каждой строке) на k черных клеток меньше, то получилось k(101-k) черных клеток. При этом, мы также добавим k(101 - k) черных клеток перекрашивая в противоположный цвет нетронутые после первого действия строки. Значит, в итого, у нас получится 2k(101 - k) черных клеток. Как теперь это максимизировать?

Подсказка 3

Ну конечно, понятно как, это же парабола ветвями вниз. Тогда, выходит, что максимум свой она принимает в двух точках : 50 и 51. Осталось(для пущей строгости и более качественного понимания сюжета) убедиться, что такая оценка точно достижима, но кажется, мы делали здесь равносильные преобразования.

Показать ответ и решение

Пусть перекрашивается сначала $k$ строк, затем $k$ столбцов. После первого этапа перекрашивания каждый столбец будет содержать $k$ чёрных и $101− k$ белых клеток. Так как $101− k$ столбцов будут нетронуты, то суммарно в таких столбцах будет $k(101−$ $k)$ чёрных клеток. В каждом из перекрашенных столбцов $101− k$ чёрных клеток, значит суммарно в таких столбцах $(101− k)k$ чёрных клеток. Итак, всего чёрных клеток $f(k)=$ $2k(101 − k).$ Понятно, что графиком функции $f(x)=2x(101− x)$ является парабола, ветви которой смотрят вниз. Значит наибольшее значение функции $f(x)= 2x(101− x)$ достигается в точке $101 a= 2$ , и функция сначала возрастает до этой точки, а потом убывает. Но значит при любых целых $k$ выполнено $f(k)≤f(50)$ при $0≤ k≤ 50$ и $f(k)≤ f(51)$ при $51≤ k≤ 101$ . Остаётся заметить, что $f(50)= f(51)= 5100$ .

Замечание. Анализ поведения функции $f(x)$ может быть проведён с использованием производной. Из того факта, что наибольшее значение функции $f(x)$ достигается в точке $101 a= 2--$ , не следует вывод о том, что функция $f(k)$ (по целым $k$ ) должна достигать наибольшего значения в одной из ближайших к $a$ целых точек. Хотя это верно для нашей функции, в общем случае существует контрпример. Для верного вывода нужна ссылка на монотонность.

Ответ: 5100

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#43948

Германн и Чекалинский разложили на столе 13 различных карт. Каждая карта может лежать в одном из двух положений: рубашкой вверх или рубашкой вниз. Игроки должны по очереди переворачивать по одной карте. Проигрывает тот игрок, после хода которого повторится какая-то из предыдущих ситуаций (включая изначальную). Первый ход сделал Чекалинский. Кто сможет выиграть независимо от того, как будет играть соперник?

Подсказки к задаче

Подсказка 1

Очень часто в играх на позиции помогает разбиение всех позиций на пары. Как это можно сделать в этой игре?

Подсказка 2

Заметим, что все позиции можно разбить на пары, отличающиеся ориентацией лишь одной карты! Осталось лишь придумать стратегию)

Показать ответ и решение

Выигрышная стратегия Чекалинского состоит в том, чтобы каждый раз переворачивать одну и ту же карту (например, пиковую даму). Все возможные позиции можно разбить на пары, отличающиеся лишь расположением пиковой дамы. Если в ответ на ход Чекалинского Германн тоже перевернёт пиковую даму, то повторится предыдущая позиция, и он проиграет. Поэтому он вынужден переворачивать другую карту. А Чекалинский, перевернув в ответ пиковую даму, получит позицию, парную к той, которая только что была. Таким образом, каждым ходом Германну придётся “начинать” новую пару, и Чекалинский всегда сможет сделать ответный ход, “закончив” пару. Так как количество возможных позиций конечно, то рано или поздно Германн не сможет открыть новую пару и проиграет.

Ответ: Чекалинский

Ошибка.
Попробуйте повторить позже

Задача 13#43946

Антон положил на клетчатую доску $46×101$ несколько бумажных крестиков, изображенных на рисунке (каждый крестик покрывает ровно 5 клеток доски). Оказалось, что для каждой клетки доски сумма попавших на неё чисел не превосходит 2. Какое наибольшее количество крестиков мог положить Антон?

$PIC$

Подсказки к задаче

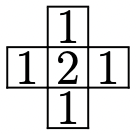
Подсказка 1

Понятно, что двойки не могут попасть на рамку. Очень часто в задачах на оценку+пример помогает разбиение на фигуры, в которых мы точно сможем определить количество двоек. На какие?

Показать ответ и решение

Отметим центральные клетки всех положенных Антоном крестиков. Эти клетки не могут лежать на границе доски, поэтому они располагаются в прямоугольнике $44×99.$ Разобьем его на $22⋅33$ прямоугольных блока $2× 3.$ Несложно проверить, что в каждом таком блоке не может находиться больше 2 центральных клеток. Поэтому на доске находится не более $2⋅22 ⋅33= 44⋅33$ крестиков.

Приведем пример расположения такого количества центральных клеток. Разобьем весь прямоугольник $44× 99$ на диагональные ряды одного направления и отметим все клетки каждой третьей диагонали. В каждую полоску $1× 3$ попадёт ровно одна отмеченная клетка, поэтому их будет ровно $44⋅33$ штуки. Легко убедиться, что условие при этом будет выполняться.

Итого $44⋅33= 1452.$

Ответ: 1452

Ошибка.
Попробуйте повторить позже

Задача 14#43643

Высоты неравнобедренного остроугольного треугольника $ABC$ пересекаются в точке $H$ . $O$ — центр описанной окружности треугольника $BHC$ . Оказалось, что центр $I$ вписанной окружности треугольника $ABC$ лежит на отрезке $OA$ . Найдите градусную меру угла $BAC$ . В ответ внесите число.

Подсказки к задаче

Подсказка 1

Нам дали условие на центр окружности BHC. Но с первого взгляда непонятно, как привязать этот центр к нашей картинке. Из условия мы знаем, что центр лежит на биссектрисе. Но тогда какой точкой с известными свойствами является центр O?

Показать доказательство

Из условия задачи следует, что точка О лежит на пересечении биссектрисы угла $A$ и серединного перпендикуляра к стороне $BC$ . Так как эти прямые пересекаются на описанной окружности треугольника $ABC$ , то О лежит на этой окружности и является серединой дуги $BC.$ Кроме того, $∘ ∠BHC = 180 − ∠BAC$ , так как $H−$ ортоцентр треугольника $ABC.$ Далее можно рассуждать по-разному.

$PIC$

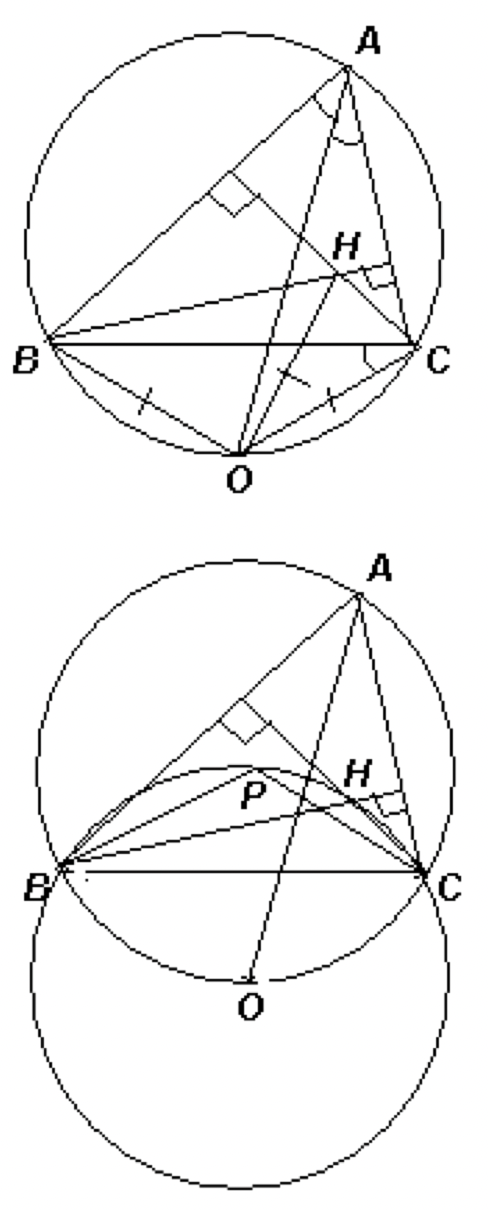
Первое решение.

Обозначим углы треугольника $ABC :∠A =α,∠B = β,∠C =$ $γ$ . (см. рис. 9.6а) Тогда $∘ ∠OCB = ∠OAB = α∕2,∠BCH =90 − β,∠OCH = ∠OCB+$ $∘ ∠BCH = 90 + α∕2− β.$

В треугольнике $OHC :OH = OC$ (радиусы одной окружности), поэтому $∘ ∠OHC = ∠OCH = 90 +α∕2− β.$ Аналогично, $∘ ∠OHB = ∠OBH = 90 +α∕2− γ.$ Тогда $∘ ∘ ∘ ∠BHC = ∠OHB +∠OHC =90 + α∕2− γ +90 + α∕2− β = 180 + α− γ− β = 2α$ Так как $∘ ∠BHC = 180 − α$ , то получим уравнение $∘ 2α= 180 − α$ , откуда $α=$ $∘ 60 .$

Второе решение.

Воспользуемся тем, что окружность, описанная около треугольника $BHC$ , симметрична описанной окружности треугольника $ABC$ относительно прямой $BC$ (см. рис. 9.6б). Тогда центр $P$ описанной окружности треугольника $ABC$ лежит на дуге $BHC$ . Следовательно, $∠BHC = ∠BPC = 2∠BAC$ . Из того, что $180∘− ∠BAC =2∠BAC$ , получим: $∠BAC =60∘$ .

Ошибка.
Попробуйте повторить позже

Задача 15#43642

В треугольнике $ABC$ , в котором $AB > AC$ , проведена биссектриса $AL.$ На стороне $AB$ выбрана точка $K$ так, что $AK = AC$ . Пусть $O$ — центр окружности, описанной около треугольника $ALB.$ Докажите, что углы $KCB$ и $ABO$ равны.

Подсказки к задаче

Подсказка 1

Сделали чертеж, теперь надо доказать параллельность. Это можно делать через равные углы при прямых или через присутствие этих прямых в фигурах, которые по определению имеют параллельные прямые.

Подсказка 2

Заметим, что треугольник ECD - равнобедренный, и у него есть биссектриса DL, которая так же является медианой и высотой, следовательно, точка L-середина ED.

Подсказка 3

Слишком много середин разных отрезков, К и М у нас уже соединены, может стоит соединить К и L?

Подсказка 4

Рассмотрите треугольник EBC, чем здесь является KL?

Подсказка 5

Правильно, это средняя линия, значит она параллельна стороне BC и равна ее половине, а так же KL параллельна стороне AD и равна ее половине MD. Отсюда KL=MD, KL||MD, а значит KLMD-параллелограмм, в котором DL||KM.

Показать доказательство

Первое решение.

$PIC$

Вписанный угол $BAL$ в два раза меньше центрального угла $BOL$ , значит, $∠BOL = 2∠BAL =∠KAC$ .

Значит, углы $KAC$ и $BOL −$ равные углы при вершинах равнобедренных треугольников $KAC$ и $BOL$ , поэтому $∠AKC =∠OBC.$

Но угол $AKC −$ внешний для треугольника $KBC$ , поэтому $∠AKC =∠ABC +∠KCB$ , в частности $∠OBC = ∠AKC > ∠ABC$ , поэтому точка $O$ лежит по другую сторону от $AB$ , нежели $C.$

С другой стороны, $∠OBC = ∠ABC + ∠ABO$ , откуда и следует утверждение задачи.

Второе решение.

$PIC$

Обозначим углы треугольника $∠BAC = 2α,∠ABC = 2β$ , $∠ACB =2γ.$ По условию, $β < γ.$ Тогда $∘ ∠ALB = ∠ACL +∠LAC = α +2γ > 90$ , поэтому $O$ лежит по другую сторону от $AB,$ нежели $L,$ и

∠OBA = ∠OAB = (180∘− ∠AOB )∕2=∠ALB − 90∘ = (α +2γ)− (α +β +γ)= γ− β

С другой стороны, в равнобедренном $\text{[math]}$ треугольнике $AKC$ имеем

∠KCB = ∠ACB − ∠ACK = 2γ− (β+γ)= γ− β =∠OBA

Ошибка.
Попробуйте повторить позже

Задача 16#43641

Пусть $M$ и $N$ — середины гипотенузы $AB$ и катета $BC$ прямоугольного треугольника $ABC$ соответственно. Вневписанная окружность треугольника $ACM$ касается стороны $AM$ в точке $Q$ , а прямой $AC −$ в точке $P.$ Докажите, что точки $P,Q$ и $N$ лежат на одной прямой.

Подсказки к задаче

Подсказка 1

Есть вневписанная окружность, есть точки касания -> хочется отметить центр окружности и все прямые углы, связанные с радиусами. Также у нас есть MN, который как-то хочется связать с остальными объектами. Как?

Подсказка 2

Продлим MN и докажем, что D лежит на ней! Вот мы знаем, что P симметрична Q относительно AD, т.е. AD перпендикулярна PQ. Если мы сможем доказать, что PN тоже перпендикулярна AD, то мы докажем требуемое в задаче.

Подсказка 3

Для этого мы покажем, что D лежит на биссектрисе угла CMB и найдем ее, а также немного посчитаем углы ;) Для требуемого в предыдущей подсказки покажем, чему равна сумма углов PAD и APN!

Показать доказательство

Пусть $D$ — центр вневписанной окружности треугольника $ACM$ , тогда $P$ и $Q$ — проекции точки $D$ на прямые $AC$ и $AB$ соответственно (см. рис.).

$PIC$

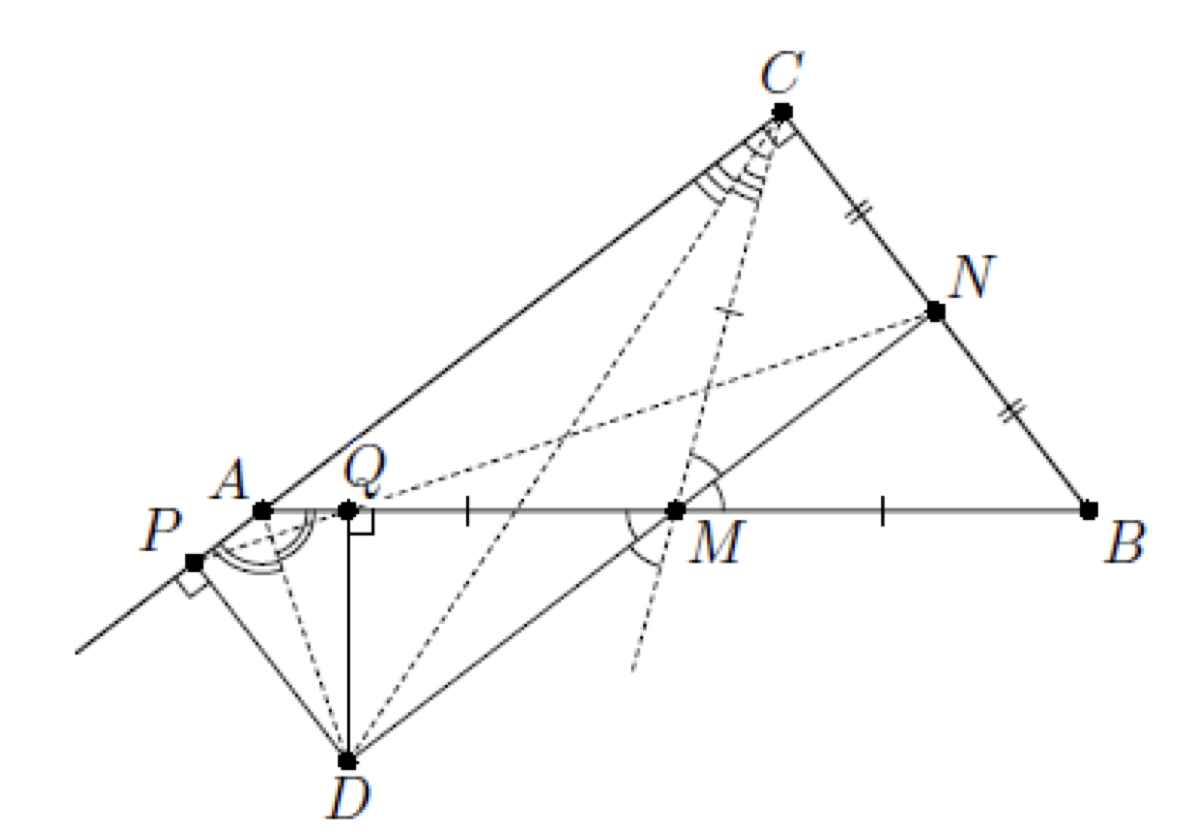
Так как $MN$ — медиана равнобедренного треугольника $BMC$ , проведённая к основанию, то $MN$ — биссектриса угла $BMC$ , поэтому точка $D$ лежит на прямой $MN.$ Кроме того, $MN −$ средняя линия треугольника $ABC$ , значит, $MN ||AC.$ Таким образом, $P CND$ — прямоугольник. Пусть $∠AMD = ∠CMN = ∠ACM =α$ , тогда $∘ ∠PAD = 1∕2(180 − α)$ , а $∠APN = ∠PCD = α∕2(CD −$ биссектриса угла $ACM ).$ Следовательно, $∘ ∠P AD+ ∠AP N =90$ , поэтому $AD ⊥ PN.$ Поскольку точка $Q$ симметрична точке $P$ относительно прямой $AD$ , то $Q$ лежит на $P N$ , что и требовалось доказать.

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#43640

Из вершины тупого угла $A$ треугольника $ABC$ опущена высота $AD.$ Проведена окружность с центром $D$ и радиусом $DA$ , которая вторично пересекает стороны $AB$ и $AC$ в точках $M$ и $N$ соответственно. Найдите $AC$ , если $AB = c,AM =m$ и $AN = n.$

Подсказки к задаче

Подсказка 1

Высота в прямоугольном треугольнике создаст множество различных, удобных для нас подобий, давайте опустим высоты DP и DQ на стороны AB и AC соответственно. Подумайте, какие именно пропорции будут удобны нам для дальнейшего решения.

Подсказка 2

Если вы правильно выбрали пропорции из подобий прямоугольных треугольников на картинке, то заметили, что AP*AB=AD^2 и AQ*AC=AD^2, следовательно, AP*AB=AQ*AC. Подумайте, как от этого выражения перейти к тому, в котором AC будет выражаться через AB, AM, AN (Воспользуйтесь тем, что треугольники ADM и ADN - равнобедренные)

Показать ответ и решение

Докажем, что $AM ⋅AB = AN ⋅AC.$ Это можно сделать по-разному.

Первый способ. В прямоугольных треугольниках $ADB$ и $ADC$ проведём высоты $DP$ и $DQ$ соответственно (см. рис. 10.4a). Тогда $2 AP ⋅AB = AD =AQ ⋅AC.$ Так как треугольники $ADM$ и $ADN −$ равнобедренные, то $1 AP = 2AM$ и $1 AQ = 2AN$ .

Заменив $AP$ и $AQ$ в равенстве $AP ⋅AB =AQ ⋅AC$ , получим требуемое.

$PIC$

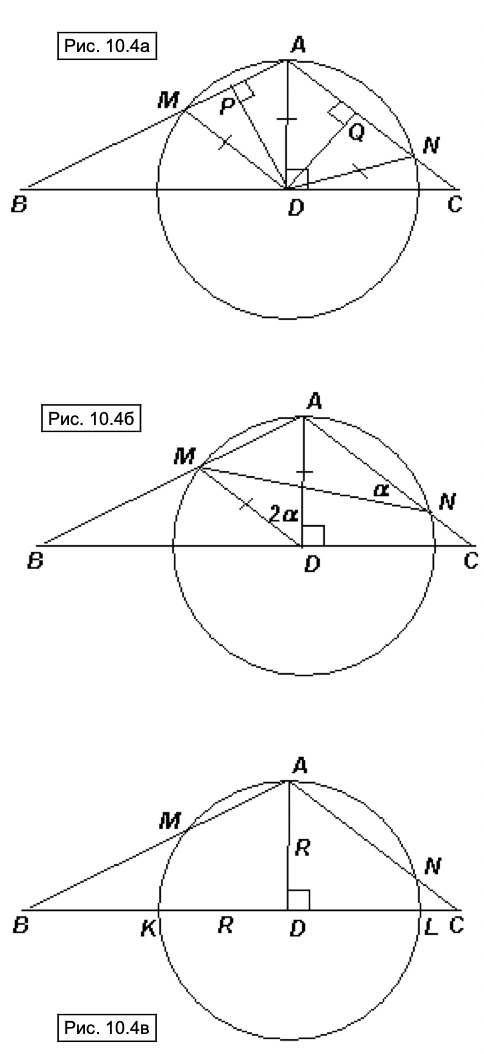
Второй способ. Докажем, что четырёхугольник BMNC вписанный, тогда требуемое равенство будет следовать из теоремы об отрезках секущих, применённой к точке $A$ и окружности, описанной вокруг четырёхугольника BMNC (см. рис. 10.46).

Пусть $∠ANM = α$ , тогда $∠AOM =2α$ (вписанный и центральный углы, опирающиеся на одну и ту же дугу). Кроме того, из равнобедренного треугольника $∘ ADM :∠MAD = 90 − α$ , поэтому $∠ABC = α.$ Из равенства $∠ABC =∠ANM$ следует, что BMNC - вписанный.

После того, как доказано указанное равенство, достаточно подставить в него данные из условия задачи и получить ответ.

Третий способ. Пусть данная окружность пересекает отрезки $BD$ и $CD$ в точках $K$ и $L$ соответственно, а ее радиус равен $R$ (см. рис. 10.4в). Тогда по теореме об отрезках секущих: $BA ⋅BM = BL ⋅BK$ , то есть $c(c− m)= BK (BK +2R).$ Из треугольника $ABD$ по теореме Пифагора: $c2 = (BK +R )2+ R2 =$ $2R2 +BK2 + 2BK ⋅R.$ Следовательно, $c(c− m)= c2− 2R2$ , откуда c. $m = 2R2$ .

Проведя аналогичное рассуждение для стороны $AC$ , получим, что $AC ⋅n= 2R2.$ Тогда $AC = mcn$ .

Ответ:

$mc n$

Ошибка.
Попробуйте повторить позже

Задача 18#43639

В остроугольном треугольнике $ABC$ проведены высоты $AD$ и $CE.$ Точки $M$ и $N$ — основания перпендикуляров, опущенных на прямую $DE$ из точек $A$ и $C$ соответственно. Докажите, что $ME = DN$ .

Подсказки к задаче

Подсказка 1

Мы провели две высоты. У нас получился четырёхугольник AEDC. Что о нём можно сказать?

Подсказка 2

Верно, он является вписанным. К тому же центр описанной окружности — это середина AC, так как AC диаметр. Давайте теперь посмотрим, какая фигура у нас получилась из построения? А какое дополнительное построение тогда напрашивается из нынешней подсказки?

Подсказка 3

Ага, это же прямоугольная трапеция, в которой мы можем провести среднюю линию OK. Выходит, MK=KN. А середина AC (пусть О) - тот самый центр нашей окружности. Зная, что OK перпендикуляр к NM и факт из прошлого предложения, какой вывод можно ещё сделать?

Подсказка 4

Верно, OK будет ещё медианой в треугольнике OED, так как OE=OD, как радиусы. Теперь только осталось вспомнить, что за дополнительное построение у нас было, и победа!

Показать доказательство

Так как $∠ADC = ∠AEC$ , то четырехугольник $AEDC$ - вписанный. Далее можно рассуждать по-разному.

$PIC$

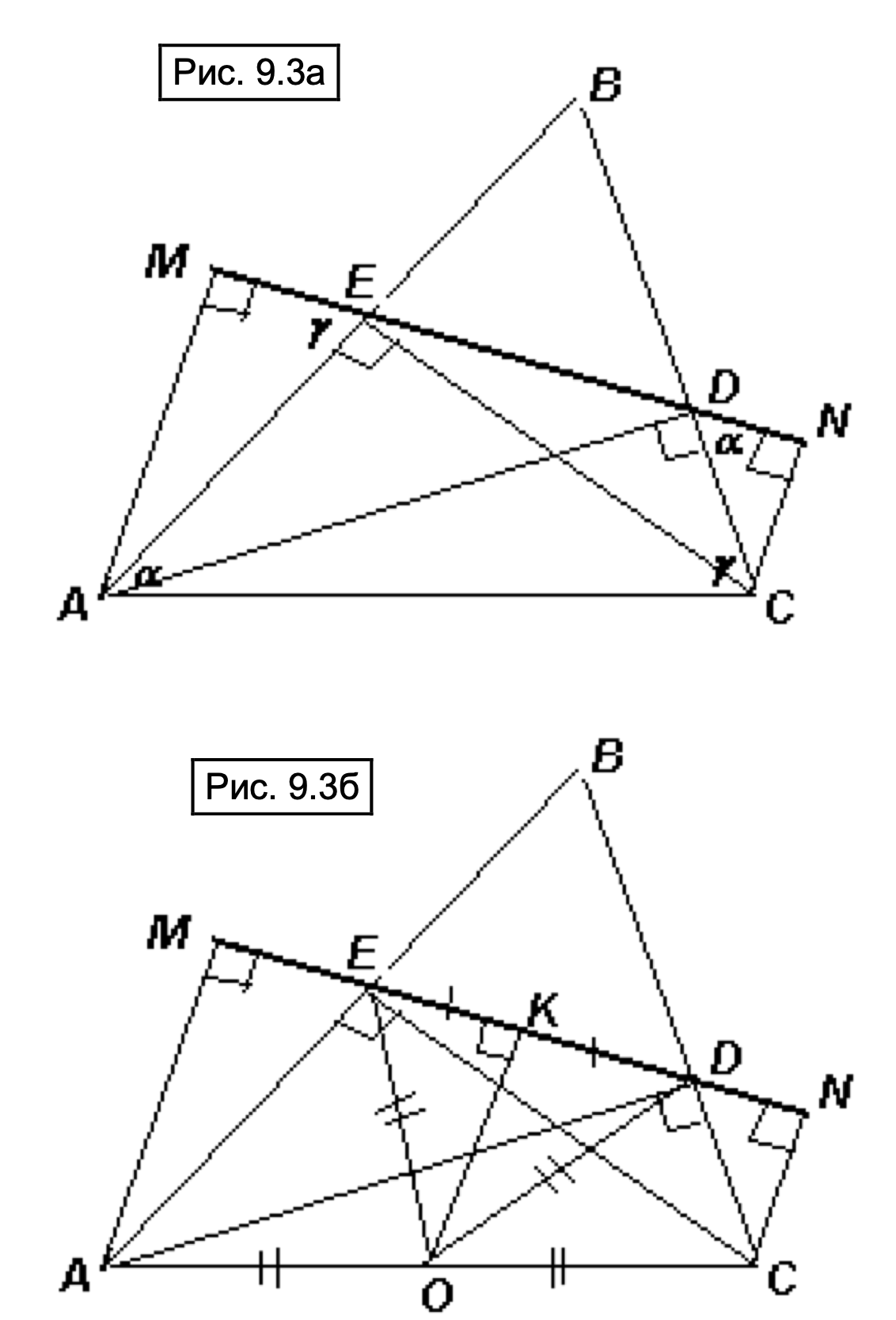
Первое решение.

По свойству вписанного четырехугольника (см. рис. 9.3а)

∠NDC = ∠BAC = α,∠MEA =∠BCA =γ

Тогда, используя прямоугольные треугольники $AME$ и $AEC$ , получим

ME = AE⋅cosγ = AC ⋅cosα⋅cosγ

Аналогично,

DN =DC ⋅cosα= AC ⋅cosγ⋅cosα

Следовательно, $ME = DN$ .

Замечание. Отметим, что использованные равенства углов можно получить из подобия треугольников $DBE$ и $ABC$ , которое, в свою очередь, можно получить из подобия треугольников $ABD$ и $CBE$ (если не использовать окружность).

Второе решение.

Воспользуемся тем, что центром окружности, описанной около $AEDC$ , является середина $O$ стороны $AC$ . Так как треугольник $DOE −$ равнобедренный, то его высота $OK$ является и его медианой, те есть $EK = KD$ (см. рис. 9.3б). Прямые $AM, OK$ и $CN$ перпендикулярны прямой $ED$ , поэтому параллельны друг другу. Из того, что $AO = OC$ по теореме Фалеса следует, что $MK = KN$ . Тогда

ME = MK − EK = KN − KD = DN

Замечание. В этом способе решения необязательно “напрямую” использовать окружность. Равенство $OE =OD$ следует из того, что эти отрезки являются медианами прямоугольных треугольников с общей гипотенузой, проведёнными к ней.

Ошибка.
Попробуйте повторить позже

Задача 19#42264

Сравните между собой наименьшие положительные корни многочленов

2016 2016 x +2016x − 1 и x − 2016x +1.

Подсказки к задаче

Подсказка 1

Попробуйте оценить наименьший положительный корень у первого многочлена. Например, стоит вспомнить, что если в одной точке у многочлена значение положительное, а в другой - отрицательное, то между этими точками есть корень)

Подсказка 2

Вот у первого многочлена в точке 0 - значение отрицательное, а в точке 1/2016 - положительное! То есть, его наименьший положительный корень точно меньше 2016. А может ли быть такой корень у второго многочлена?

Подсказка 3

Поймите, что второй многочлена всегда положителен на отрезке [0; 1/2016]. Например, с помощью производной или с помощью знания того, что x²⁰¹⁶ положительный, а 2016x-1 - отрицательный на этом отрезке)

Показать ответ и решение

Первое решение.

Пусть $x1 >0$ — корень уравнения $2016 x + 2016x− 1= 0$ , а $x2 > 0$ — корень уравнения $2016 x − 2016x+ 1=0$ . Тогда

x2016+ 2016x − 1= 0 12016 1 x2 − 2016x2+ 1= 0

Складывая эти равенства почленно, получаем:

2016 2016 x1 + x2 + 2016(x1− x2)= 0

Значит

x20116+x22016 x1 − x2 = −--2016----< 0

Таким образом, $x1 < x2.$

Второе решение.

Функция $x2016$ принимает только положительные, а функция $2016x − 1−$ только отрицательные значения на интервале $(0,1∕2016).$ Значит, уравнение $x2016 = 2016x− 1$ и многочлен $x2016− 2016x+ 1$ не имеют корней на этом интервале. Многочлен $x2016+ 2016x − 1$ принимает в концах отрезка $[0,1∕2016]$ значения разных знаков и, следовательно, имеет корень на интервале $(0,1∕2016)$ .

Ответ: у первого меньше

Ошибка.
Попробуйте повторить позже

Задача 20#42263

Рассмотрим множество квадратных трёхчленов вида $x2+ 2mx +n2$ , где $m$ и $n$ различные натуральные числа от $1$ до $100.$ Каких больше квадратных трёхчленов — тех, что имеют корни, или тех, которые не имеют корней?

Подсказки к задаче

Подсказка 1

Понятно, что сразу хочется рассмотреть дискриминант) он будет равен 4m² - 4n². Может тут есть какая-то симметрия?

Подсказка 2

Вспомните, что m и n - различные числа, и если есть трехчлен x² + 2mx + n², то есть и x² + 2nx + m²)

Показать ответ и решение

Из условия на коэффициенты следует, что рассматриваемых квадратных трёхчленов конечное число. Разобьём это множество квадратных трехчленов на пары: $2 2 x + 2mx+ n$ и $2 2 x +2nx+ m .$ Эти трехчлены имеют дискриминанты $2 2 m − n$ и $2 2 n − m .$ Поскольку $m$ и $n$ различные числа, в каждой паре один из трёхчленов имеет корни, другой не имеет корней. Таким образом, этих трёхчленов поровну.

Ответ: поровну

Предыдущий раздел

Следующий раздел