Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике проведена биссектриса
. Диаметр
его описанной окружности перпендикулярен прямой
(порядок точек на описанной окружности
). Окружность, проходящая через точки
и
, пересекает отрезки
и
в точках
и
соответственно. Докажите, что если
, то
.
Подсказка 1
Если сделать аккуратный чертеж, то кажется, что продолжения ХТ, АК и YС пересекаются в одной точке на описанной окружности треугольника АВС.
Подсказка 2
Предыдущий факт сложно доказывать напрямую, стоит применить обратный ход.
Подсказка З
Обозначим пересечение луча АК с описанной окр-тью АВС за L. Пересечение LХ и LY с ВС обозначим Т₁ и Z₁. Хотим показать, что XТ₁Z₁Y является вписанным. Используя, что дуги ВL и LС равны (из-за биссектрисы), можно посчитать сумму противоположных углов данного четырехугольника. Следующий шаг — показать равенство Т₁К и КZ₁.
Подсказка 4
Чтобы показать равенство Т₁К и КZ₁:
Подсказка 5
Осталось показать, что такой четырехугольник единственный. Пересечением чего является центр описанной окружности вписанного четырехугольника? Посмотрите, где лежит центр окружности описанной около XT₁Z₁Y.
Применим обратный ход. Обозначим пересечение луча с
за
Пересечение
и
с
обозначим
и
Теперь
нам надо доказать, что
вписанный и
так как получится, что точки
и
из условия совпадают с
ними.
![]()
Тогда получили, что вписанный, так как внутренний угол равен противоположному внешнему. Теперь обратим внимание на
то, что треугольники
и
подобные, а в прямоугольном треугольнике высота и медиана образуют равны углы со сторонами.
Поэтому так как
высота в треугольнике
то
является медианой в треугольнике
Значит,
середина
откуда получаем то, что мы хотели в начале.
Заметим, что четырехугольник из условия единственный, ведь его центр лежит на серединном перпендикуляре к и на
перпендикуляре к
восставленному в
Ошибка.
Попробуйте повторить позже
Высоты остроугольного треугольника
пересекаются в точке
На касательную, проведенную из точки
к
описанной окружности треугольника
опущен перпендикуляр
(точка
лежит внутри треугольника
).
Докажите, что окружность, проходящая через точку
и касающаяся прямой
в точке
касается также и прямой
Источники:
Подсказка 1
На картинке даны какие-то касательные, присутствуют хорды - ну не просто же так! Стоит отметить равные между собой вписанные уголки в двух окружностях. Хочется доказать, что A₁Q- касательная…нет ли случайно походе конструкции на чертеже?
Подсказка 2
Из того, что AB - касательная, следует, что в двух окружностях на чертеже есть отсеченные дуги, равные удвоенному углу CAB. Мы знаем, что CQ - касательная. А хочется, чтобы A1Q стала касательной…можно ли их как-то связать? А как связать между собой окружности?
Подсказка 3
Если мы найдем преобразование, которой переведет СQ в А1Q, а окружности друг в друга, то мы сможем доказать, что A1Q тоже является касательной!
Обозначим через описанную окружность треугольника
а через
— окружность, проходящую через точку
и
касающуюся прямой
в точке
Хорды
и
этих окружностей отсекают от них дуги одинаковой угловой величины. В
самом деле, половины этих дуг в обоих случаях равны
: для окружности
это вписанный угол, а для
— угол между
касательной и хордой.
Заметим также, что угол между прямыми и
равен углу между прямыми
и
эти вписанные углы опираются на
одну дугу
в окружности с диаметром
![]()
Точку пересечения прямой с окружностью
обозначим через
и выделим на картинке два фрагмента: в окружности
проведена
секущая
и на ней выбрана точка
в окружности
проведена секущая
и на ней выбрана точка
В каждом из этих двух
фрагментов из точек на секущих проведены прямые под одинаковыми углами к секущим:
и
Первая из них касается
и нам
нужно доказать, что вторая касается
Для доказательства нужно установить, что две описанные конфигурации подобны. Мы проверим
это двумя способами. Углы треугольника, как обычно, будем обозначать греческими буквами, соответствующими названиям
вершин.
Способ 1.(подсчёт отношения отрезков)
Угловые величины отсекаемых секущими дуг равны, поэтому остаётся проверить, что Отношение хорд
и
(стягивающих равные дуги) равно отношению диаметров окружностей. Диаметр окружности
равен
диаметр окружности
равен
Таким образом,
С другой стороны, отношение высот
равно отношению
сторон
которое по теореме синусов тоже равно
![]()
Способ 2.(Поворотная гомотетия)
Рассмотрим поворотную гомотетию с центром в точке переводящую точку
в
и
в
Она существует, ибо
треугольники
и
подобны(и подобны треугольнику
). Окружность
перейдёт в
ибо друг в
друга переходят хорды
и
отсекающие равные дуги. При этом секущая
окружности
переходит в
секущую
окружности
и, следовательно, точка
переходит в точку
Значит, первый фрагмент переходит во
второй.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике с углом
при вершине
проведены высоты
и
Луч
пересекает прямую
в точке
Оказалось, что
Найдите углы треугольника
Источники:
Подсказка 1
Даны параллельность и вписанность - это сразу же намекает нам на углы! Попробуем поотмечать, а потом воспользуемся условием на угол A) Что узнаем?
Подсказка 2
Понимаем, что AF = FC! Теперь мы можем посчитать достаточно большое количество углов на картинке...но все из них равны либо 90, либо 90/2. На что это может намекать? Обратим внимание на точку F.
Подсказка 3
Угол AFC в 2 раза больше чем AXC. Чем тогда является F для треугольника AXC? Когда мы это поймем, мы сможем по аналогии связать углы AFX=EFB и ACB. Не забываем про вписанность!)
![]()
Из условия следует, что . Из вписанностей
, и теперь из параллельности
. В треугольнике
точка
оказалась центром описанной окружности (равноудалена от вершин
и
и центральный угол в два раза больше вписанного).
Поэтому
, что вместе со вписанностью
дает
Ошибка.
Попробуйте повторить позже
Точка — середина основания
трапеции
вписанной в окружность
Биссектриса угла
пересекает отрезок
в
точке
Прямая
вторично пересекает окружность
в точке
Из точки
проведены касательные
и
к описанной окружности треугольника
Докажите, что прямые
и
пересекаются в одной точке.
![]()
Источники:
Решение 1.
Пусть луч пересекает описанную окружность в точке
— середине дуги
Заметим, что
Следовательно, описанная окружность треугольника проходит через точку
Кроме того,
прямой, поэтому прямая
содержит диаметр этой окружности. Пусть прямая
пересекает этот диаметр в точке
а прямая
пересекает его в точке
![]()
Для решения задачи требуется установить, что Пусть
и
— центр и радиус этой окружности. Точка
обладает известным
свойством:
Поэтому нам осталось проверить, что
Обозначим
Тогда Это означает, что треугольник
и
подобны и
Решение 2.
Как и предыдущем решении, докажем, что Для этого достаточно проверить, что
![]()
Мы докажем, что обе эти четвёрки гармонические. Заметим, что четырёхугольник гармонический, так как касательные в точках
и
пересекаеются на
Проецируя эту четвёрку точек из точки
на прямую
получим
С другой стороны,
проецируя четвёрку
из точки
на прямую
получим
где — бесконечно удалённая точка направления
Осталось заметить, что, так как
— середина дуги
а
— середина
отрезка
прямая
— серединный перпендикуляр к основанию вписанной трапеции
Следовательно,
— середина
отрезка
и
Ошибка.
Попробуйте повторить позже
Высоты и
остроугольного треугольника
пересекаются в точке
Окружность с центром в точке
проходит через
точки
и середину отрезка
Окружность с центром в точке
проходит через точки
и середину отрезка
Докажите, что
Источники:
Прежде всего, обозначим середину отрезка через
а окружность, проходящую через
и
— через
Поскольку для решения задачи достаточно доказать неравенство
(и, аналогично,
Это неравенство следует из удивительного факта: расстояние от точки до прямой
равно в точности
Докажем его двумя
способами: в обоих мы обнаружим на окружности
ещё одну точку.
Решеение 1.
Пусть точка симметрична вершине
относительно прямой
Проверим,
что она лежит на окружности Для этого достаточно проверить, что
В самом деле,
последнее равенство следует из вписанности четырехугольника
Таким образом, центр окружности
должен лежать на серединном перпендикуляре к её хорде
Значит, расстояние от
до
равно расстоянию между этим серединным перпендикуляром и прямой
то есть между серединами отрезков
и
Оно в два раза меньпе, чем расстояние от
до
т. е. равно
Решение 2.
Отметим такую точку что
Пусть
тогда
С другой стороны, медиана прямоугольного треугольника
равна
и
3начит,
Итак,
и
Следовательно, четырехугольник
— равнобедренная
трапеция, так что
лежит на окружности
т. е. на
Поскольку центр лежит на серединном перпендикуляре к
расстояние от него до
равно
что и
требовалось.
Ошибка.
Попробуйте повторить позже
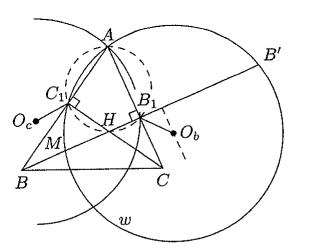
В неравнобедренном треугольнике проведена биссектриса
Точка
— центр вписанной окружности треугольпика
Серединный перпендикуляр к отрезку
пересекает окружность, описанную около треугольника
в точках
и
Точка
на отрезке
выбрана так, что
Докажите, что точки
и
лежат на одной
окружности.
Источники:
Обозначим через середину дуги
описанной окружности треугольника
не содержащей точку
Тогда точка
лежит на
прямой
и по лемме о трезубце точка
равноудалена от точек
и
, поэтому
лежит на отрезке
и является центром
описанной окружности треугольника
. Следовательно,
Первое решение.
Из подобия треугольников и
следует, что
Тогда и, значит, треугольники
и
подобны. Следовательно,
Аналогично и, значит, треугольники
и
подобны. Следовательно,
Таким образом,
Стало быть, точки и
лежат на одной окружности.
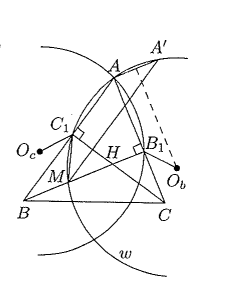
Второе решение.
Пусть точка симметрична
относительно серединного перпендикуляра х
Очевидно,
— равнобедренная трапеция,
значит
,
лежат на одной окружности.
Докажем, что точка лежит на этой же окружности. Заметим, что точка
лежит на
поскольку
равноудалена от точек
и
т. е.
— диаметр окружности с центром
и радиусом
Из подобия треугольников
и
следуег, что
что равносильно равенству
Из последнего равенства следует, что точки
лежат
на одной окружности.
Ошибка.
Попробуйте повторить позже
Точка — центр вневписанной окружности треугольника
касающейся стороны
в точке
а точка
диаметрально
противоположна точке
на описанной окружности этого треугольника. На отрезках
выбраны точки
соответственно таким образом, что
где r — радиус вписанной окружности треугольника
Докажите, что точки
лежат на одной окружности.
Подсказка 1
У нас в условии есть центры вписанной и вневписанной окружностей - попробуем посчитать какие-то углы, найти равные…хочется еще равные отрезки как-то использовать, не так ли? Еще заметим, что точки Z, T у нас практически одинаковы по построению, поэтому будет досрочно сделать выводы для одной из них, а потом произнести волшебное «аналогично». Не понятно, как подобраться к углам требуемого «вписанного» четырехугольника, поэтому попробуем доказать, что серединные перпендикуляры к его стороны пересекаются в одной точке.
Подсказка 2
С помощью подсказки 1, учитывая, что угол АВА´ прямой, приходим к тому, что ZBIaY равнобедренная трапеция! Что мы тогда может сказать о серединной перпендикуляре к ZY? А к BIa? Серединный перпендикуляр к последнему отрезку несложно найти с помощью известной леммы, которая ищет такую точку W, что WB = WIa. Аналогичные действия проделывает и с точкой T)
Подсказка 3
Серединные перпендикуляры к ZY и YT проходят через середину дуги BC окружности (ABC) по лемме о Трезубце и в силу того, что эти серединные перпендикуляры совпадают с серединными перпендикулярами к BIa и CIa. Осталось лишь доказать, что серединный перпендикуляр к XY проходит через эту же точку.
Подсказка 4
Для этого отложим на продолжении отрезка XIa за Х такую точку I’, что XI’ = r и подумаем о треугольнике IaI’I.
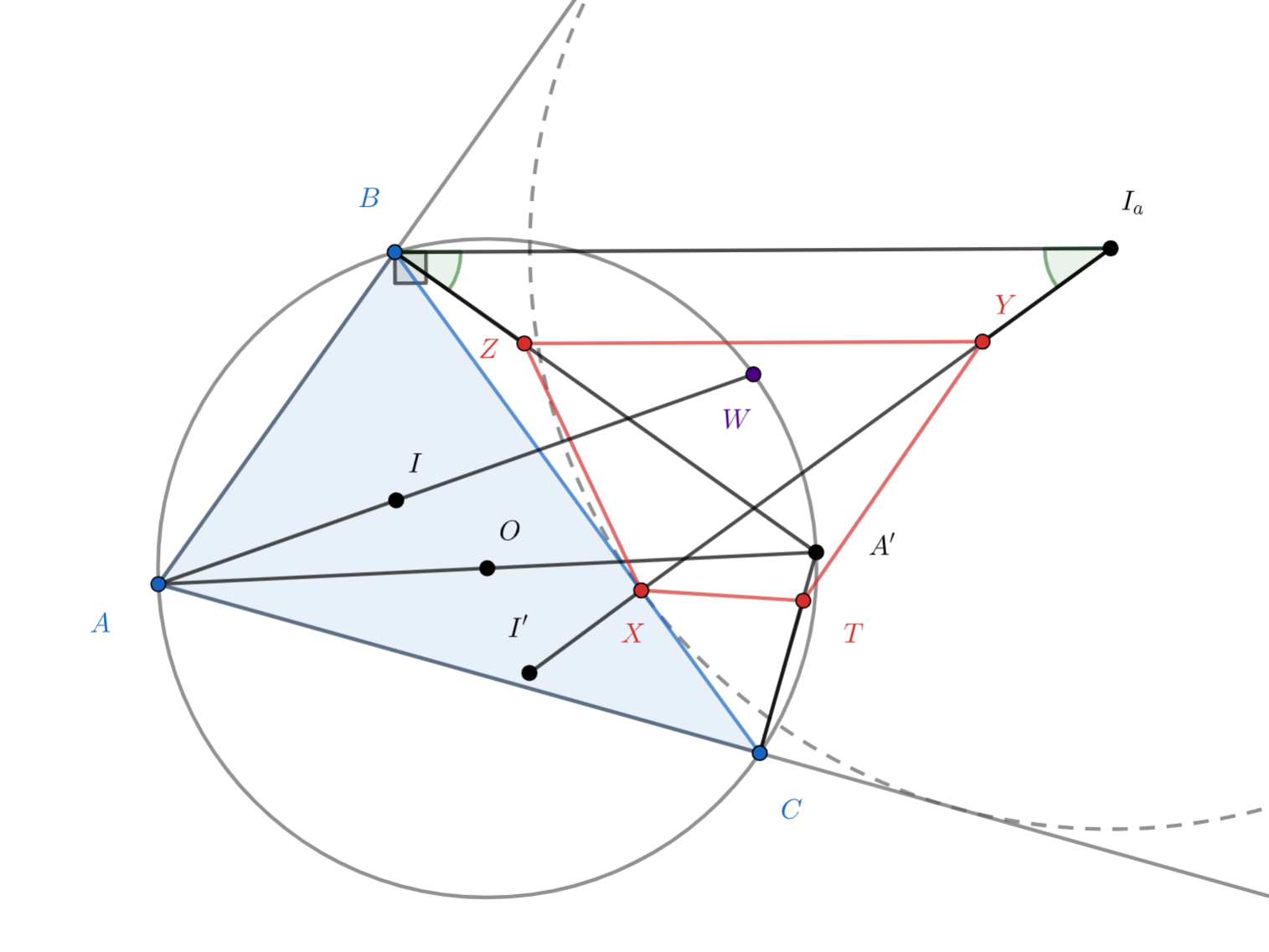
Из условия сразу следует, что . Кроме этого, если
— центр вписанной окружности, то
. Из этих равенств сразу
следует, что
. Поскольку прямая
— внешняя биссектриса угла
, угол
, и
поэтому
Таким образом, и
. Это значит, что четырехугольник
— равнобедренная трапеция. Поэтому
серединный перпендикуляр к отрезку
совпадает с серединным перпендикуляром к отрезку
. Последний по лемме о трезубце
проходит через середину
дуги
описанной окружности треугольника. Аналогично, через
проходит и серединный перпендикуляр
к отрезку
Осталось понять, почему через проходит серединный перпендикуляр к отрезку
. Отметим на продолжении
отрезка
за точку
такую точку
, для которой
. Иными словами,
— прямоугольный треугольник с
прямым углом при вершине
. По уже упоминавшейся лемме о трезубце, точка
— середина его гипотенузы
.
Следовательно, она лежит на серединном перпендикуляре
совпадающем с серединным перпендикуляром к отрезку
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике проведена биссектриса
Точка
— центр вписанной окружности треугольника
Серединный перпендикуляр к отрезку
пересекает окружность, описанную около треугольника
в точках
и
Точка
на отрезке
выбрана так, что
Докажите, что точки
и
лежат на одной
окружности.
Подсказка 1
У нас есть треугольник AIC и его описанная окружность. Может, мы знаем что-то хорошее про ее центр?
Подсказка 2
По лемме о трезубце, это середина дуги AC! Обозначим ее за O. Кроме того, он лежит на отрезке ED, т.к. это серединный перпендикуляр к AC. Как можно теперь связать точки E и D так, чтобы можно было что-то сделать с точкой F похожим образом?
Подсказка 3
Например, можно сказать, что E и D симметричны относительно прямой, перпендикулярной ED и проходящей через O) Давайте также отразим F относительно этой прямой, и получим точку F'. Что мы получили?
Подсказка 4
Мы получили, что есть DEFF' - вписанная равнобокая трапеция. Мы хотим доказать, что E, D, B, F на одной окружности, а уже есть DEFF'..Как можно переформулировать теперь задачу?
Подсказка 5
Можно теперь доказывать, что точки F', D, B и E лежат на одной окружности) Для этого попробуйте доказать, что O - центр окружности B₁FF'! Это можно сделать с помощью симметрии, чтобы доказать, что O лежит на B₁F') А дальше как действовать?
Подсказка 6
А дальше можно воспользоваться подобием треугольников OAB и OAB₁ и записать отношения сторон) После с помощью предыдущей подсказки можно по-другому выразить это равенство отношений, и получится требуемое условие для того, чтобы F', D, B и E лежали на одной окружности)
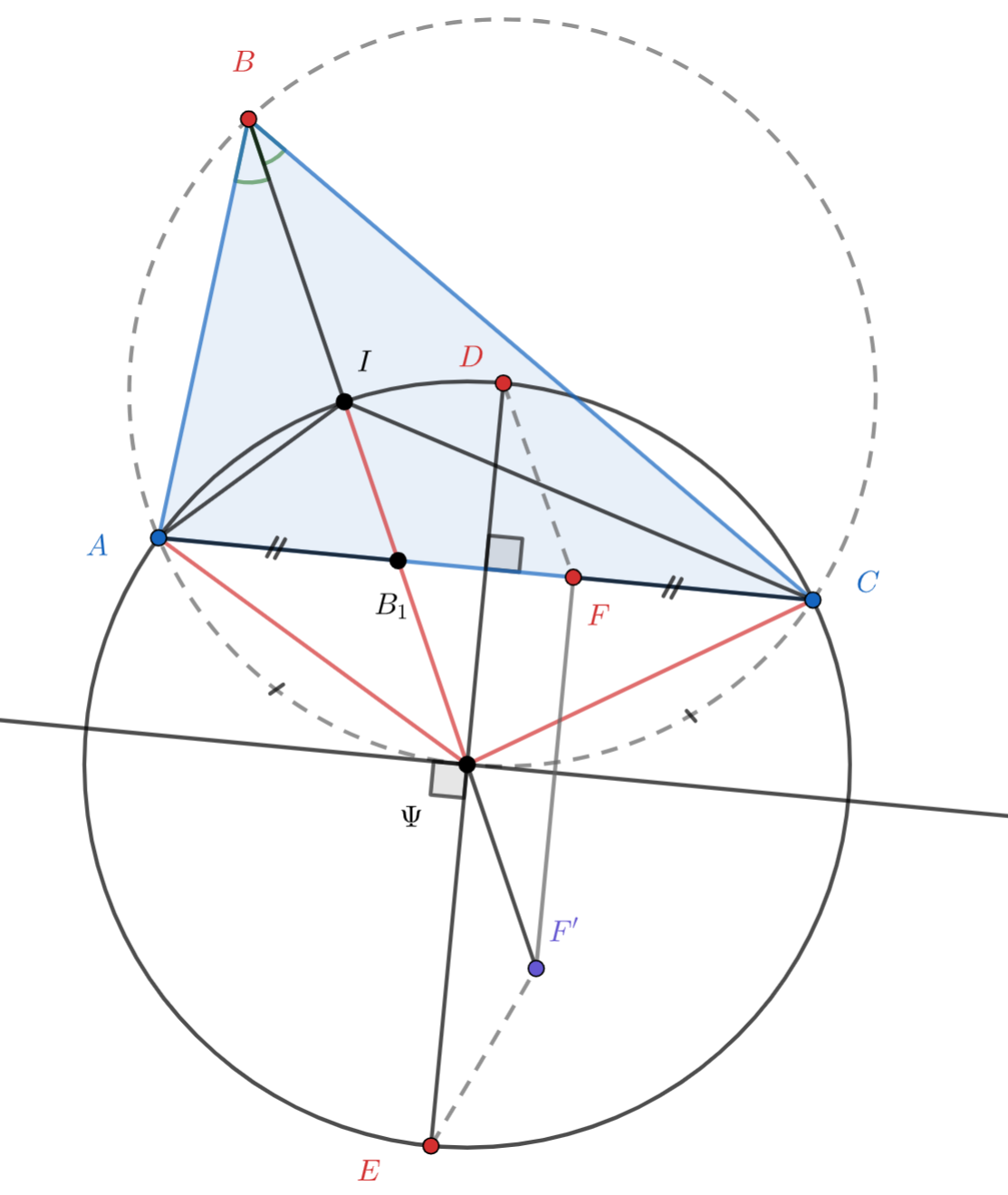
Обозначим через середину дуги описанной окружности треугольника
, не содержащей точку
. Тогда
лежит на
прямой
. Кроме того, по лемме о трезубце точка
равноудалена от точек
и
, поэтому
является центром
описанной окружности треугольника
и
лежит на отрезке
. Пусть точка
симметрична точке
относительно
серединного перпендикуляра к
. Очевидно,
— равнобедренная трапеция, значит,
лежат на одной
окружности.
Докажем, что точка лежит на этой же окружности. Заметим, что точка
лежит на
, поскольку
равноудалена от точек
и
, т.е.
— диаметр окружности с центром
и радиусом
. Из подобия треугольников
и
следует, что
, что равносильно равенству
Из последнего равенства следует, что точки лежат на одной окружности.
Ошибка.
Попробуйте повторить позже
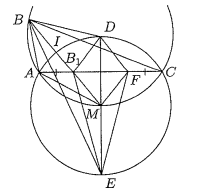
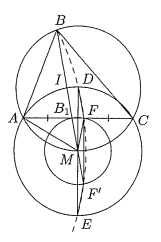
Треугольник вписан в окружность
с центром
Прямая
вторично пересекает окружность
в точке
Точки
и
— середины сторон
и
соответственно. Прямые
и
пересекают окружность
вторично в точках
и
а также пересекают сторону
в точках
и
соответственно. Описанные окружности
треугольников
и
пересекаются в точках
и
Докажите, что точки
и
лежат на одной прямой.
![]()
Источники:
Решение 1.
Сделаем поворот с центром в точке переводящий
в
и обозначим образ точки
при этом повороте через
Пусть
— точка пересечения прямых
и
Из равенства дуг
и
легко следует равенство углов
Тогда описанная окружность треугольника
при этом повороте переходит в описанную
окружность треугольника
При этом точка
очевидно, будет иметь одинаковые степени относительно этих двух
окружностей.
Аналогично, рассмотрев поворот с центром в переводящий
в
и обозначив образ точки
через
и точку пересечения
с
через
мы получим, что точка
имеет одинаковые степени относительно описанных окружностей треугольников
и
![]()
Таким образом, вместо утверждения “точка лежит на прямой
”, эквивалентного тому, что точка
имеет одинаковые
степени относительно описанных окружностей треугольников
и
достаточно доказать, что точка
имеет одинаковые степени относительно описанных окружностей треугольников
и
т.е. что точки
и
совпадают.
Заметим, что медиана треугольника лежит на прямой
и
Значит,
— симедиана
треугольника
и тогда четырехугольник
гармонический. Аналогично, четырехугольник
также
гармонический. Но тогда обозначив через
точку пересечения прямых
и
мы получим равенство двойных
отношений
откуда
Решение 2.
Пусть прямая пересекает описанную окружность треугольника
в точках
и
а прямая
пересекает описанную
окружность треугольника
в точках
и
Тогда
Кроме того,
следовательно, Значит треугольники
и
подобны и одинаково ориентированы.
Из этого, учитывая, что треугольники и
также подобны, получаем
Аналогично
Из этих равенств и параллельности и
следует, что
![]()
Докажем, что точка лежит на луче
(и, аналогично, на луче
). Для этого сначала заметим, что хорда
окружности
пересекает во внутренних точках стороны
и
следовательно, один конец хорды лежит на дуге
а другой — на дуге
(здесь и далее рассматриваются дуги с концами в двух вершинах треугольника
не содержащие третью вершину). Аналогично один
из концов хорды
лежит на дуге
а другой — на дуге
Это возможно, только если точки
и
лежат на дугах
и
соответственно. Из этого следует, что углы
и
треугольника
острые, а также что точки
лежат на прямой именно в таком порядке. Далее заметим, что треугольник
ориентирован так же, как
треугольник
по доказанному выше; треугольник
ориентирован так же, как треугольник
поскольку точки
и
лежат на продолжениях сторон
и
за точки
и
соответственно; наконец,
треугольник
ориентирован так же, как треугольник
поскольку
Итак, треугольники
и
ориентированы одинаково, а это и означает, что точка
лежит на луче
По доказанному выше
имеем
Следовательно, степени точки относительно описанных окружностей треугольников
и
равны.
Ошибка.
Попробуйте повторить позже
Неравнобедренный треугольник периметра
вписан в окружность
Точки
и
— середины дуг
и
соответственно. Касательная, проведенная к окружности
в точке
пересекает луч
в точке
Оказалось, что середина отрезка
лежит на прямой
Найдите длину отрезка
Источники:
Пусть — центры вневписанных окружностей треугольника
касающихся сторон
и
соответственно. Тогда
прямые
— биссектрисы треугольника
, а прямые
— его внешние биссектрисы. Следовательно,
точки
будут основаниями высот треугольника
а окружность
— его окружностью девяти точек. Тогда точки
является отличной от
точкой пересечения
с
Следовательно,
— середина
Аналогично,
— середина
Таким образом,
— средняя линия треугольника
Обозначим через и
соответственно основания внешней и внутренней биссектрис угла
треугольника
и через
— точку
пересечения прямых
и
По условию мы знаем, что
![]()
Точка лежит на луче
, поскольку
— на
так что
Тогда а поскольку треугольник
прямоугольный, то и
Следовательно, — прямоугольник и
Мы получаем, что прямые
и
параллельны
и имеют общую
точку
Тогда эти прямые совпадают. Это означает, что точка
лежит на средней линии треугольника
и, следовательно, делит
пополам отрезок
Далее, применив свойство внешней биссектрисы к треугольникам и
, получим
Тогда и, следовательно,
Ошибка.
Попробуйте повторить позже
На окружности отмечены точки
и
Касательные к окружности
проведённые в точках
и
пересекаются в точке
Пусть
— середина отрезка
Окружность
проходящая через точки
и
вторично пересекает отрезок
в точке
и
окружность
— в точках
и
Докажите, что касательные, проведенные к окружности
в точках
и
пересекаются на
отрезке
Источники:
Обозначим через центр окружности
Поскольку
— высота прямоугольного треугольника
то
поэтому (и аналогично
) — касательные к окружности
Но тогда касательные к окружности
в этих точках
перпендикулярны касательным к
из точки
и значит, они проходят через центр
лежащий на диаметре
![]()
Ошибка.
Попробуйте повторить позже
На биссектрисе угла остроугольного треугольника
выбрана точка
Окружность
построенная на
как на диаметре,
пересекает стороны
и
в точках
и
соответственно. Окружность, проходящая через вершину
и касающаяся
в точке
вторично пересекает прямую
в точке
Окружность, проходящая через вершину
и касающаяся
в точке
вторично
пересекает прямую
в точке
Докажите, что
Источники:
Решение 1.
Отметим сначала полезное свойство касающихся окружностей, а потом перейдём к решению задачи. Если секущая проходит через
точку
касания двух окружностей, то вписанные углы, опирающиеся на высекаемые ей дуги, равны. Действительно,
поскольку вписанный угол равен углу между касательной и секущей, имеем равенство
![]()
Теперь перейдем к решению задачи. Пусть — основание биссектрисы угла
Точки
и
симметричны относительно прямой
поэтому
и треугольники
и
равны. Из касания окружностей в точке
имеем равенство
поэтому четырёхугольник
вписанный. Из касания окружностей в точке
имеем равенство
значит, четырёхугольник
также вписанный. Отметим, что описанные окружности четырёхугольников
и
равны, поскольку они являются описанными окружностями равных треугольников
и
Хорды
и
этих
окружностей лежат напротив углов
и
Поскольку равны углы, эти хорды также равны.
![]()
Решение 2.
Рассмотрим гомотетию с центром переводящую окружность, проходящую через вершину
и касающуюся
в точке
в
окружность
Эта гомотетия переводит точку
в точку
а точка
— в точку
вторичного пересечения прямой,
параллельной
и проходящей через
с окружностью
Тогда точки
лежат на одной прямой. Аналогично
точки
тоже лежат на одной прямой. Рассмотрим прямую
С одной стороны, она является биссектрисой угла
поскольку
— середина дуги
С другой стороны, угол
опирается на диаметр, значит, он прямой и
не только биссектриса, но и высота треугольника
Тогда
— серединный перпендикуляр к
поэтому
![]()
Ошибка.
Попробуйте повторить позже
Окружность, проходящая через вершины и
треугольника
пересекает стороны
и
в точках
и
соответственно. Медиана из вершины
делит дугу
этой окружности пополам. Докажите, что треугольник
равнобедренный.
![]()
Источники:
Пусть — середина стороны
— середина дуги
лежащая на отрезке
— точка, симметричная точке
относительно медианы
Предположим противное. Тогда
и
![]()
Таким образом, и
— основания вписанной, а следовательно, равнобочной трапеции
Значит,
и
треугольники
и
равны по трем сторонам. Противоречие: один из двух равных треугольников не может лежать внутри
другого.
Ошибка.
Попробуйте повторить позже
Окружность, вписанная в треугольник касается стороны
в точке
Отрезок
повторно пересекает окружность в точке
Точки
и
на окружности таковы, что
и
Докажите, что прямая, соединяющая центры вписанных окружностей
треугольников
и
перпендикулярна биссектрисе угла
![]()
Источники:
Пусть и
— точки касания вписанной окружности треугольника
со сторонами
и
coответственно, а точки
и
—
центры вписанных окружностей треугольников
и
Известно, что касательная, параллельная хорде, проходит через середину
дуги, которую стягивает хорда.
![]()
Из чего следует, что точка лежит на прямой
а точка
— на прямой
По свойству касательной
поэтому
треугольники
и
подобны и имеет место равенство
И по аналогичным соображениям
Но
а значит,
Далее заметим, что по лемме о трезубце для треугольников и
получаем, что
и
соответственно.
Подставляя в последнее равенство, получаем, что
откуда Но нам известно, что
перпендикулярен биссектриссе угла
Тогда из параллельности биссектриса
перпендикулярна и
Ошибка.
Попробуйте повторить позже
Дан выпуклый четырехугольник Описанная окружность треугольника
пересекает стороны
и
в точках
и
соответственно. Описанная окружность треугольника
пересекает стороны
и
в точках
и
соответственно.
Оказалось, что четырехугольник
— параллелограмм. Докажите, что и четырехугольник
— параллелограмм.
![]()
Источники:
Заметим, что по свойствам вписанных углов, откуда
Аналогично,
Следовательно,
симметрия относительно точки пересечения диагоналей параллелограмма
переводит треугольник
в треугольник
, в
частности,
отображается в
. Тогда точка пересечения прямых
и
переходит в точку пересечения симметричных им прямых
и
т. е.
переходит в
Таким образом, четырехугольник
симметричен относительно той же точки, и значит,
является параллелограммом.
![]()
Ошибка.
Попробуйте повторить позже
Точка — середина дуги
описанной окружности треугольника
— центр его вписанной окружности,
— основание
биссектрисы
Прямая
пересекает описанную окружность в точке
Описанная окружность треугольника
пересекает
прямую
вторично в точке
Докажите, что
![]()
Источники:
Решение 1.
Обозначим через середину дуги
а через
— точку пересечения прямой, проходящей через
перпендикулярно
с прямой
Докажем, что
Для этого докажем, что четырёхугольник
вписанный, проверив равенство углов
Не умаляя общности, можно считать, что (тогда точка
рассположена на луче
). Заметим, что
(так как
— диаметр), поэтому описанная окружность
треугольника
касается прямой
в точке
Поскольку
описанная окружность
треугольника
(с центром в
) тоже касается
в точке
Следовательно, точка
— радикальный центр
и описанной окружности
Но тогда точки
лежат на одной прямой,
откуда
![]()
Решение 2.
Не умаляя общности, можно считать, что Обозначим через
середину дуги
Тогда
поскольку сумма дуг описанной окружности на которые опираются углы в последней сумме, равна
Так как
(он опирается на диаметр), то точки
лежат на одной прямой. Далее, в силу подобия треугольников
и
выполняется равенство
откуда
Но в силу леммы о трезубце,
поэтому
откуда
и треугольники
и
подобны. Но тогда
![]()
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
выбраны точки
и
соответственно, отрезок
параллелен
Окружность,
проходящая через
и
пересекает отрезок
в точке
Известно, что описанная окружность треугольника
касается
прямой
Докажите, что
Источники:
Заметим, что по свойству касательной а по свойству вписанных углов
![]()
Таким образом, в трапеции углы
и
равны. Значит, эта трапеция равнобедренная, откуда следует, что
Тогда по свойству касательной и секущей
Последний переход сделан с помощью неравенства о средних, откуда получаем неравенство из задачи.



