Ошибка.
Попробуйте повторить позже
Турист прибыл на остров, где живут 100 волшебников, каждый из которых может быть рыцарем или лжецом. Он знает, что на
момент его приезда один из ста волшебников — рыцарь (но не знает, кто именно), а остальные — лжецы. Турист может
выбрать любых двух волшебников и
и попросить
заколдовать
заклинанием Вжух!, которое меняет сущность
(превращает рыцаря в лжеца, а лжеца в рыцаря). Волшебники выполняют просьбы туриста, но если в тот момент волшебник
— рыцарь, то сущность
действительно меняется, а если
— лжец, то не меняется. Турист хочет после нескольких
последовательных просьб одновременно знать сущность хотя бы
волшебников. При каком наибольшем
он сможет добиться своей
цели?
Докажем, что ни в один момент времени ни про какое множество волшебников нельзя доказать, что в нём четное число рыцарей (из этого будет следовать оценка, ведь если нам в какой-то момент удалось определить сущность двоих волшебников, то либо мы доказали, что в их паре четное число рыцарей, либо это рыцарь и лжец, и мы еще за одну операцию сделаем из них двух рыцарей, подействовав рыцарем на лжеца).
Изначально такого множества точно нет. Рассмотрим первый момент, когда удалось про некоторое множество доказать, что в нем
четное число рыцарей. Пусть последним ходом «Вжух!» говорил волшебник
. Несложным переборов вариантов можно убедится, что на
прошлом ходу симметрическая разность
и
тоже содержала четное количество рыцарей, что противоречит выбранному первому
такому моменту.
_________________________________________________________________________________________________________________________________________________________________________________
Пример. Пусть все волшебники с -го по
-го поменяют сущность
-го. Легко видеть, что в результате он в любом случае станет
рыцарем.
Ошибка.
Попробуйте повторить позже
На плоскости отмечено 100 точек общего положения (т.е. никакие три не лежат на одной прямой). Докажите, что можно выбрать три
отмеченные точки ,
,
так, чтобы для любой точки
из оставшихся 97 отмеченных точек, прямые
и
не содержали бы
точек, лежащих внутри треугольника
.
Подсказка 1
Прямые, соединяющие точки A, B, CЮ делят плоскость на 7 частей, включая треугольник внутри. Рассмотрите эти части. Точки D из каких частей нам подходят?
Подсказка 2
Видно, что подходящие части тем больше, чем больше угол АВС. Воспользуемся принципом крайнего и возьмём такие 3 точки, чтобы АВС был максимальным. Проверим, подходит ли нам этот случай, пойдя от противного: пусть они не подходят. Тогда в каких частях может находиться точка D?
Подсказка 3
Верно, а теперь попробуйте получить противоречие через сумму углов, зная, что угол АВС максимальный из всех возможных
Применим принцип крайнего: выберем среди всех троек точек треугольник с самым большим углом
Предположим, что точки ,
,
не подходят. Тогда существует точка
в объединении частей плоскости, одна из которых
заключена между прямыми
и
а другая — между прямыми
и
При этом не может лежать внутри треугольника
, иначе
.
Рассмотрим случай, когда лежит между лучами
и
(когда
и
лежат в разных полуплоскостях относительно
).
Тогда
получаем противоречие. То же работает для случая, когда лежит между лучами
и
.
Оставшиеся два случая (когда и
лежат в разных полуплоскостях относительно
) рассматриваются аналогично: в
них
Ошибка.
Попробуйте повторить позже
Таблица заполнена числами как показано на рисунке:
| 1 | 2 | 3 | … | 100 |
| 101 | 102 | 103 | … | 200 |
| | | | | |
| 9901 | 9902 | 9903 | … | 10000 |
Можно ли переставить некоторые числа так, чтобы в каждой клетке по прежнему стояло одно число, и чтобы во всех прямоугольниках из трех клеток сумма чисел не изменилась?
Подсказка 1
Часто задачи с таблицами решаются раскрасками. А какая раскраска имеет какие-то приятные свойства для прямоугольников из трех клеток?
Рассмотрим раскраску таблицы в три цвета, как показано на рисунке:
| 1 | 2 | 3 | … | 1 |
| 2 | 3 | 1 | … | 2 |
| 3 | 1 | 2 | … | 3 |
| | | | | |
| 1 | 2 | 3 | … | 1 |
Если в исходной таблице к числам цвета 2 прибавить единицу, а из чисел цвета 3 вычесть единицу, то мы получим такую перестановку, что набор чисел сохранится. А сумма в каждой тройке тоже.
Ошибка.
Попробуйте повторить позже
Есть карточек, на каждой написано число от
до
(каждое — ровно на двух карточках). Карточки лежат на столе числами вниз.
Набор из
карточек называется хорошим, если на них каждое число встречается по одному разу. Барон Мюнхаузен утверждает, что он
может указать
наборов по
карточек, из которых хотя бы один заведомо окажется хорошим. При каком наибольшем
слова барона
могут быть правдой?
Источники:
Подсказка 1
Задача непростая, поэтому давайте сначала "причёсывать" её, наблюдать какие-то интересные свойства. Например, если у нас набор из n карточек хороший, то оставшиеся n карточек тоже образуют хороший набор(пусть дополнительный набор). Понятно, что слишком большое n взять не получится. Попробуйте изучить, перебрать какие-то n. Понятно, что n=10, наверное, уже слишком много, а n=5, n=6 маловато.
Подсказка 2
Надеюсь, вы порешали сами задачку, и догадываетесь какое примерно максимальное n, а может у вас получилось построить пример для него. При n = 8 и больше уже указать такой набор будет нельзя, т.е. ответ к задаче n = 7. Понятно, что если докажем для 8, то и для больших тоже. Наша цель — предъявить такой способ разметки карточек, чтобы ни один из 80 выбранных наборов не оказался хорошим. Давайте в наших 80 произвольных наборах рассмотрим какую-то карточку A. Можем ли мы сделать так, чтобы она была во всех наборах?
Подсказка 3
Да, меняя наш набор на дополнительный, мы добьёмся присутствия A во всех наборах. А дальше нам глобально нужно убрать плохие наборы, чтобы остались хорошие, но в конце концов, продолжая так делать, всё равно останется плохой набор. Мы докажем, что всегда можно так занумеровать карточки, что все 80 наборов окажутся плохими. Давайте этим и займёмся. Попробуйте понять с помощью принципа Дирихле, хотя бы сколько ещё других карточек B у нас будет? Тогда сколько наборов у нас может оказаться плохими, если цифра на B будет такая же, как у A?
Подсказка 4
Давайте просто аккуратно посчитаем. Оставшихся карточек всего у нас 80 * 7 = 560. А оставшихся карточек, кроме A, у нас 15. Отсюда по принципу Дирихле у нас будет хотя бы 38 карточек B(обозначение из предыдущей подсказки). И вот теперь у нас есть хотя бы 38 наборов с карточками A и B! Тогда пусть на них и оказалось какое-то число 8, теперь все эти наборы плохие. У нас остались 14 карточек(A и B мы убрали) и не больше 42 наборов, где в теории ещё может быть хороший. А теперь аналогично делаем дальше! Попробуйте проделать эти же шаги самостоятельно(их не так много, поэтому лучше, чтобы избежать путаницы и ошибок, сделать всё). Теперь, дойдя до конца процесса, поймите, почему мы доказали оценку? Сколько наборов и карточек остаётся на последнем шаге?
Подсказка 6
Ага, на последнем шаге должен был остаться 1 набор и 4 карточки. Тогда, написав на двух из них число 2, а на двух других число 1, мы победим(даже с запасом)! Мы доказали то, что было написано в 3 подсказке. Осталось разобраться с примером. Мы увидели, что 80 карточек хватает с запасом, поэтому, скорее всего, достаточно брать меньше наборов и среди них будет один хороший. Подумайте, сколько будет достаточно? Это число явно выражается через n.
Подсказка 7
Покажем, что для 2n карточек, мы можем выбрать 2^(n-1) наборов, среди которых точно есть один хороший. Это можно сделать по индукции. База понятна. Пусть на столе лежит 2n+2 карточки, а для 2n мы доказали. Попробуем взять 2 произвольные карточки. Какие варианты тогда возможны? Нужно рассмотреть их и применить предположение индукции!
Подсказка 8
Ага, возможны два варианта: мы вытащили карточки с одинаковыми числами или с различными. Первый случай совсем несложный и делается почти сразу. А во втором попробуйте объединить оставшиеся непарные карточки мысленно в одну и снова применить предположение индукции. Повозитесь со всем этим и у вас получится! Ну а исходную задачу мы тем самым решаем, так как 64<80. Победа!
Заметим, что если набор из карточек хороший, то набор из оставшихся
карточек тоже хороший(назовём его дополнительным
набором).
Покажем, что для нельзя так указать
наборов, чтобы хотя бы один из них оказался хорошим. Для этого достаточно
убедиться в том, что при
нельзя указать такие
наборов. Поскольку, барон выбирает наборы карточек, не зная, какие числа
написаны на этих карточках снизу, мы можем считать, что изначально на карточках не было никаких надписей, а числа на карточках
появляются уже после того, как выбор сделан. Наша цель — предъявить такой способ разметки карточек, чтобы ни один из
выбранных
наборов не оказался хорошим.
Итак, пусть выбрано наборов. Рассмотрим произвольную карточку
Меняя некоторые наборы на дополнительные, можно
добиться того, что карточка
будет присутствовать во всех наборах. Перечислим с учётом кратности все остальные карточки,
встречающиеся в этих наборах. Всего будет перечислено
карточек. Кроме карточки
у нас имеется
карточек,
значит, какая-то из них встретится не менее
раз(так как
), назовём её карточкой
Напишем на
карточках
и
число
тогда те
(или более) наборов, в которых встречаются обе эти карточки, будут плохими.
Уберём карточки
и
останется
карточек и
(или менее) набора, среди которых должен найтись хотя бы один
хороший.
Аналогично зафиксируем одну из оставшихся карточек и переделаем наборы так, чтобы карточка
входила во все наборы.
Выписав все остальные карточки, встречающиеся в наборах, получим
карточки. Поскольку, помимо карточки
у нас
имеется
карточек, какая-то из них — назовём её
— встретится
раз(так как
). Напишем на карточках
и
число 7 — в результате все эти наборы станут плохими. Уберём карточки
и
останется
карточек и
набора, среди которых
опять должен найтись хороший.
Действуя аналогично, получим, что какие-то две карточки встретятся вместе хотя бы в наборах, напишем на них число
и
выкинем, останется
карточек и
наборов. Тогда, поскольку
какая-то пара карточек встретится в одном наборе хотя бы
раз. Написав на этих карточках число
и выкинув, мы получим
карточек и
наборов. Какая-то очередная пара карточек
встретится в одном наборе хотя бы
раз, напишем на них число 4 и выкинем, в результате получим
карточек и
набора.
Далее какая-то пара карточек встретится в одном наборе хотя бы
раз, записываем на них число
и выкидываем, останется
карточки и
набор. Напишем на двух карточках из этого набора число
а на двух других — число
тогда и этот
набор также окажется плохим. Мы доказали, что всегда можно так занумеровать карточки, что все
наборов окажутся
плохими.
Покажем теперь, что для карточек всегда можно выбрать
наборов так, чтобы хотя бы один из них оказался хорошим. В
нашем случае
и мы сможем выбрать
наборов, что решает задачу. Набор из
карточек, на которых записаны
различных чисел(каждое — в двух экземплярах), будем называть двойным.
Пример 1. Докажем индукцией по что для любого двойного набора из
карточек всегда можно предъявить
наборов, среди
которых есть хороший. База
очевидна.
Пусть на столе лежит двойной набор из карточек. Попробуем наудачу выбрать из них две одинаковые карточки, взяв
произвольные карточки
и
Самоуверенно отложим их в сторону. Если мы угадали, то на столе остался двойной набор из
карточек,
для которого, применив предположение индукции, можно указать
наборов, среди которых есть хороший. Теперь для каждого
указанного набора
рассмотрим наборы
Мы утверждаем, что среди наборов и
(а их в сумме получается ровно
штук) непременно найдётся хороший(для
исходного множества карточек) набор. Если карточки
и
и в самом деле одинаковые, это очевидно — подойдут даже два
набора.
Предположим теперь, что на карточках и
написаны разные числа(обозначим их также
и
). Тогда в оставшемся множестве из
карточек были “непарные” карточки с числами
и
— мысленно соединим их в новую пару и применим предположение индукции,
указав
наборов, среди которых есть хороший набор
содержащий по одной карточке из каждой пары. На самом деле он содержит
ровно одно из чисел новой пары, скажем
и по одному представителю всех остальных пар. Но тогда набор
в исходном множестве
карточек является хорошим!
Пример 2. Построим граф, вершинами которого являются карточки. Каждую пару карточек с одинаковыми числами соединим красным
ребром. Проивзольным образом разобьём карточки на пары и соединим карточки в каждой паре синим ребром. Полученный
красно-синий граф(на самом деле мультиграф, поскольку между одной парой вершин может быть проведено и красное,
и синее ребро) представляет собой несколько циклов чётной длины. Рассмотрим такой набор его вершин, что в каждом
цикле вершины выбраны через одну, назовём его чередующимся набором. Тогда в этом наборе будет присутствовать ровно
один конец каждого красного ребра и, значит, он будет хорошим. Проблема в том, что мы, т.е. Мюнхгаузен, не знаем как
именно проведены красные рёбра. Но заметим, что любой чередующийся набор содержит ровно по одной вершине каждого
синего ребра. Поэтому, указав все наборов, содержащих ровно по одной вершине каждого синего ребра, мы заведомо
укажем и чередующийся набор. Поскольку набор и его дополнение лишь одновременно могут быть чередующимися, из
каждой пары взаимодополняющих наборов достаточно брать только один. Стало быть, достаточно указать лишь
наборов.
при
Ошибка.
Попробуйте повторить позже
Клетки таблицы окрашены в белый цвет. За один ход разрешается выбрать любые
клеток из одной строки или из одного
столбца и перекрасить каждую из них в противоположный цвет — из белого в черный, а из черного в белый. За какое наименьшее
количество ходов можно получить таблицу с шахматной раскраской клеток?
Источники:
Оценка.
Покажем, что ходов обязательно придётся сделать.
Первый способ. Предположим, что мы получили шахматную раскраску. Рассмотрим диагональ, покрашенную в чёрный цвет. За ход
можно перекрасить не более одной клетки этой диагонали, следовательно, потребовалось не менее ходов.
Второй способ. Предположим, что мы сделали менее ходов. Тогда найдётся строка, которую мы не задействовали. Но в этой строке
в результате появилось
чёрных клеток, значит, было сделано как минимум
“вертикальных” ходов. Аналогично показывается, что
было сделано как минимум
“горизонтальных” ходов, т.е. всего не менее
ходов.
Пример.
Покажем, как за ходов можно получить шахматную раскраску, для этого перекрасим первый столбец без первой клетки, третий
столбец без третьей клетки, пятый столбец без пятой клетки,
й столбец без
й клетки. Дальше перекрасим первую строку без
первой клетки, третью строку без третьей клетки, пятую без пятой клетки,
ю строку без
й клетки. Тогда все клетки, у
которых номер строки и номер столбца имеют разную чётность, окажутся переркашенными ровно один раз и, значит, чёрными, а остальные
клетки будут белыми.
ходов
Ошибка.
Попробуйте повторить позже
В социальной сети у каждого пользователя не более десяти друзей (отношение “дружба” симметрично). Сеть связна: если, узнав интересную новость, пользователь начинает рассылать её своим друзьям, те своим и так далее, то в итоге новость узнают все пользователи. Докажите, что администрация сети может разбить пользователей на группы так, чтобы выполнялись следующие условия:
) каждый состоит ровно в одной группе;
) каждая группа связна в указанном выше смысле;
) одна из групп содержит от
до
членов, а каждая из остальных от
до
членов.
Источники:
Социальная сеть представляет собой граф, в котором люди - это вершины, а отношение “дружба” — ребра. Достаточно рассмотреть случай,
когда этот граф является деревом. В требованиях условия задачи группу, в которой состоит от до
членов, будем называть малой, а
группу, где от
до
членов, — большой. Докажем утверждение задачи индукцией по числу пользователей сети. База индукции:
Если в сети не более
пользователей, объявим их всех малой группой. Если в сети от
до
пользователей,
назначим малой группой любого пользователя, соответствующего висячей вершине, а всех остальных запишем в большую
группу.
Индукционный переход. Достаточно проверить, что если число пользователей больше то можно подобрать большую группу, при
удалении которой граф останется связным. Подвесим наше дерево и рассмотрим наиболее далекую от корня вершину
(одну из вершин),
у которой больше
потомков. У каждого из сыновей вершины
не более
потомков, при этом количество сыновей — не более
Если у каждого из сыновей
не более
потомков, то в сумме у
не более
потомков, что противоречит
выбору вершины
Значит, один из сыновей
имеет от
до
потомков, назначим его и его потомков большой
группой.
Ошибка.
Попробуйте повторить позже
олигархов построили себе страну с
городами, каждый олигарх владеет ровно одним городом. Кроме того, каждый олигарх построил
несколько дорог между городами: любая пара городов соединена максимум одной дорогой каждого из олигархов (между двумя городами
может быть несколько дорог, принадлежащих разным олигархам). Суммарно было построено
дорог. Некоторые олигархи
хотели бы создать корпорацию, объединив свои города и дороги так, чтобы при этом из любого города корпорации можно
было доехать до любого другого ее города по дорогам этой корпорации, возможно, заезжая по дороге в города других
олигархов. Но оказалось, что никакая группа олигархов создать корпорацию не может! При каком наибольшем
это
возможно?
Источники:
Пронумеруем олигархов и их города числами от до
соответственно.
Пример.
Пусть дорога между городами и
принадлежит олигарху под номером
тогда и только тогда, когда
Тогда
количество дорог равно
Проверим, что этот пример удовлетворяет условию задачи. Предположим, что это не так и какая-то группа олигархов смогла
создать корпорацию. Пусть — наибольший номер олигарха в этой корпорации. Тогда из города
не выходит ни одной
дороги, принадлежащей членам корпорации, что противоречит тому, что из этого города можно добраться до любого города
корпорации.
Оценка 1.
Будем говорить, что дорога если она принадлежит этому олигарху или город на одном из концов дороги
принадлежит этому олигарху. Заметим, что из города не может выходить дорога, принадлежащая владельцу этого города, так как в этом
случае владельцы городов, которые соединяет эта дорога, могут образовать корпорацию. Следовательно, любая дорога нравится ровно трём
олигархам. Сопоставим каждой дороге тройку олигархов, которым она нравится.
Рассмотрим произвольную тройку олигархов и
Докажем, что эта тройка сопоставлена не более чем одной
дороге.
Предположим, что это не так. Выбраниая тройка олигархов может быть сопоставлена всего трем дорогам (если таковые
имеются): дороге принадлежащей олигарху
дороге
принадлежащей
и дороге
принадлежащей
Легко видеть, что каким бы двум из этих дорог ни была сопоставлена тройка
эта тройка олигархов сможет
образовать корпорацию. Следовательно, каждая тройка олигархов сопоставлена не более одной дороге, т. е. дорог не более
Заметим, что в нашем примере любая тройка олигархов сопоставлена дороге
принадлежащей олигарху
т. е. всего
дорог, что дает комбинаторный способ подсчета количества дорог в примере.
Оценка 2.
Рассмотрим граф, в котором вершиины — это города, а ребра цвета — дороги, принадлежащие олигарху номер
Заметим, что если
из графа, удовлетворяющего условию задачи, удалить часть вершин, выходящие из них ребра и все ребра, принадлежащие
олигархам-владельцам удаляемых вершин, то для оставшегося графа условие задачи о невозможности построить корпорацию продолжит
выполняться.
Докажем индукцией по что если в графе
вершин, то при удалении любой вершины, всех ее ребер и всех ребер соответствующего
ей цвета суммарное количество ребер уменьшается не более чем на
База очевидна.
Переход. Пусть мы хотим удалить олигарха номер . Так как все
олигархов не могут образовать корпорацию, граф на. ребрах всех
цветов несвязен. Обозначим через
компоненту связности, содержащую город олигарха номер
, через
— объединение всех
остальных компонент связности, а через
и
— количество вершин в
и
соответственно. Тогда подграф
содержит не
более
ребер
-го цвета. Далее, из вершины
выходит не более
ребер с цветами, соответствующими
вершинам из
Наконец, применяя к графу
индукционное предположение, получаем, что в графе
имеется не более
ребер, имеющих цвет
или выходящих из вершины
Следовательно, при удалешии вершины
исчезнет не
более
ребер.
Для доказательства оценки будем по одной удалять вершины, подсчитывая, сколько ребер при этом пропадает. Получается, что мы
удалили не более ребер. Заметим, что если в нашем примере удалять олигархов в порядке убывания
номеров, то при удалении олигарха номер
будет пропадать в точности
ребер. Следовательно, в любом графе ребер не
больше, чем в построенном нами примере.
максимальное число дорог равно
Ошибка.
Попробуйте повторить позже
Близорукая ладья бьёт все клетки своей строки и своего столбца, до которых можно дойти не более чем за шагов, шагая из
клетки в соседнюю по стороне. Какое наибольшее не бьющих друг друга близоруких ладей можно расставить в квадрате
Источники:
Подсказка 1
В задачах на ходы необычных фигур полезно бывает выделить области, в которых мы точно сможем оценить количество фигур. Какие несложные фигуры для разбиения можно выбрать?
Подсказка 2
Обратим внимание на полоски из клеток. Какого размера можно их взять для разбиения, чтобы точно оценить количество ладей в них?
Подсказка 3
Полоски размером 1*61! Попробуем симметрично разбить таблицу так, чтобы использовать достаточно большое количество таких полосок. Оценка может помочь построить пример)
Оценка. В задачах на ходы необычных фигур полезно бывает выделить области, в которых мы точно сможем оценить количество
фигур. Тут оценка на самом деле следует более-менее из попытки построить пример. Реализуем здесь эту идею. Разобьём
квадрат на центральный квадрат
и
прямоугольников
В каждый прямоугольник
разбиения и в каждую горизонталь квадрата
можно поставить не более одной ладьи, поэтому ладей не более
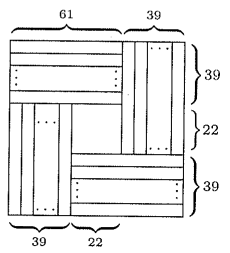
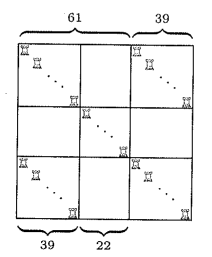
Пример. Поставим ладьи на клетки главной диагонали и двух параллельных ей диагоналей, состоящих из клеток. При такой расстановке
между ладьями, расположенными в одном столбце и одной строке, находится ровно
пустых клеток, поэтому никакие две ладьи не бьют
друг друга.
Ошибка.
Попробуйте повторить позже
Пусть между городами и
есть дороги
и
но нет дорог
и
Назовем пеpecтройкой замену пары дорог
и
на пару дорог
и
Изначально в стране было несколько городов, некоторые пары городов были
соединены дорогами, причем из каждого города выходило по
дорог. Министр нарисовал новую схему дорог, в которой из
каждого города по-прежнему выходит
дорог. Известно, что как в старой, так и в новой схемах никакие два города
не соединены более, чем одной дорогой. Докажите, что новую схему можно получить из старой с помощью нескольких
перестроек.
Источники:
Рассмотрим множество состоящее из всех возможных
-регулярных(степени всех вершин в графе равны 100) графов на
данном множестве вершин
(наши две схемы дорог — среди них). Докажем что любые два графа из
можно перевести
друг друга серией перестроек. Для двух графов
пусть
- множество необщих рёбер этих графов, а
. Очевидно, что число
всегда четно, и в множестве
поровну рёбер из
и
Предположим, что существуют пары непереводимых друг в друга перестройками графов в Рассмотрим такую прару графов
с минимальным
Граф
имеет в каждой вершине поровну рёбер из
и из
. Следовательно, в
существует
чередующийся цикл(в котором рёбра
и
чередуются). Рассмотрим цикл
с минимальным числом
вершин(это не обязательно простой цикл, вершины в нем могут повторяться). Первая наша цель - найти на этом цикле четыре
последовательные различные вершины. В самом деле, пусть среди
есть совпадающие. Очевидно, возможно
лишь совпадение
. Так как рёбра цикла не повторяются, тогда
и в качестве искомой четверки подойдет
Итак, не умаляя общности будем считать, что все вершины различны, причем
и
Рассмотрим три случая.
(а) Тогда проведем перестройку
в графе
(это возможно, так как
) и получим граф
с
По предположению,
можно получить из
перестройками, значит, можно получить и
(b) . Тогда
— чередующийся цикл, меньший чем
противоречие.
(c) Тогда проведем перестройку
в графе
(это возможно, так как
и получим
граф
с
По предположению,
можно получить из
перестройками, значит, можно получить и
Ошибка.
Попробуйте повторить позже
В начале игры у Малыша и Карлсона есть один кусок шоколадки в виде квадрата клеточек. Каждым ходом Малыш делит
какой-нибудь кусок по клеточкам на три прямоугольных куска, а Карлсон съедает один из этих трёх кусков по своему выбору. Игра
заканчивается, когда сделать очередной ход невозможно. Если всего было сделано чётное число ходов — побеждает Малыш, если нечётное —
Карлсон. Кто выигрывает при правильной игре?
Источники:
Назовем кусок шоколадки если его можно разрезать, и
если нельзя. Изначально есть только один большой кусок, а в
конце игры их
Карлсон может играть так, чтобы четность количества больших кусков после его хода обязательно менялась: один
большой кусок уничтожается ходом Малыша, после чего появляется от
до
новых больших кусков. Если количество новых больших
кусков нечетно, то один точно есть и Карлсон его съест. Если же количество больших кусков четно, то есть хотя бы один малый и Карлсон
съест именно малый кусок. Итак, число больших кусков после каждой пары полуходов меняет четность, а по окончании
игры чётность чисел больших кусков должна измениться, значит, будет сделано нечётное количество ходов, т.е. Карлсон
выиграет.
Ошибка.
Попробуйте повторить позже
На круглом ожерелье висят бусинок, каждая покрашена в красный или синий цвет. Если у какой-то бусинки соседние с ней бусинки
покрашены одинаково, ее можно перекрасить (из красного в синий или из синего в красный). Можно ли из любой исходной раскраски
бусинок сделать ожерелье, в котором все бусинки покрашены одинаково?
Источники:
Подсказка 1
Не очень хочется доказывать то, что из любой исходной раскраски можно прийти к одноцветной. Тогда попытаемся доказать, что существует раскраска, при которой нельзя перейти к одноцветной. В этом нам конечно поможет какой-то инвариант. Попробуйте подумать, какой-же...
Подсказка 2
Какой самый простой инвариант мы знаем? Инвариант по четности какой-то величины. Посмотрите на количество пар соседних красных бусинок...
Подсказка 3
Это действительно инвариант, ведь если мы имели участок ожерелья (к)(c)(к) и мы перекрасили центральный, количество увеличилось на 2, а если (к)(к)(к), уменьшилось на 2 (если мы меняли участок вида (с)(?)(c) эта величина не изменилась). В любом случае четность не поменялась. Не трудно увидеть, что тоже самое можно сказать про четность количества пар соседних синих бусинок. Как тогда построить контрпример?
Подсказка 4
Давайте посмотрим на значение инвариантов при одноцветной раскраске: в любом случае бусинок какого-то цвета не будет, а это значит, что количество таких пар будет просто 0, т.е. четное число. Тогда нам нужно придумать такой пример, что изначально количество пар соседних красных и количество пар соседних синих бусинок были нечетными числами. Я в вас верю!
Докажем, почему ожерелья с чётным количеством бусинок нам не подходят. Легко убедиться, что при любом перекрашивании
количество пар соседних бусинок вида (к)-(к) либо не меняется, либо меняется ровно на т.е. в любом случае не меняется
четность этого числа. То же самое верно и про число пар вида (с)-(с). В одноцветном ожерелье четной длины оба эти
количества четны. Поэтому из ожерелья, в котором оба эти количества нечетны, нельзя получить ни одно из двух одноцветных
ожерелий. При четном n таково, например, ожерелье (к)-(к)-(с)-(с)-
-(с)(не забываем, что у нас ожерелье имеет форму
окружности).
Ошибка.
Попробуйте повторить позже
Правильный шестиугольник разбит на равные ромбы со сторонами, параллельными сторонам шестиугольника. На трёх сторонах шестиугольника, среди которых нет соседних, задали направления в порядке обхода шестиугольника против часовой стрелки. Затем на каждой стороне ромба поставили стрелку, направленную так же, как параллельная этой стороне сторона шестиугольника. Докажите, что не существует замкнутого пути, идущего по стрелкам.
Источники:
Пусть в графе нашёлся цикл, и пусть он проходит по горизонтальному отрезку слева направо. Возьмём ромб, примыкающий к стороне
и отметим в нём параллельную сторону
Возьмём ромб, примыкающий к стороне
и отметим в нём параллельную сторону
и
т.д.
Такую же конструкцию провернём в другую сторону: возьмём ромб, примыкающий к отрезку с другой стороны, и отметим в нём
параллельную сторону
и т.д.
![]()
Мы получили “полосу ширины ”, которая рассекает наш шестиугольник. При этом цикл заведомо пересекает эту полосу, но всё время в
направлении слева направо. Это невозможно.
Ошибка.
Попробуйте повторить позже
У Васи есть карточек трёх цветов, карточек каждого цвета не больше
Докажите, что он может выложить из них квадрат
так, чтобы любые две соседние (по стороне) карточки оказались разного цвета.
Источники:
Пусть для определённости карточки были красного, синего и зеленого цветов и меньше всего было карточек зелёного цвета. Тогда зелёных
карточек не более Покрасим клетки квадрата
в шахматном порядке так, что левый нижний угол квадрата
чёрный. Начнём раскладывать красные карточки на черные клетки, начиная с левого нижнего угла квадрата. Сначала
будем заполнять слева направо чёрные клетки из нижней строки, затем также слева направо чёрные клетки из второй
снизу строки и т.д. до тех пор, пока не разложим все красные карточки. Далее разложим синие карточки на белые клетки,
начиная с левого верхнего угла доски. Сначала будем заполнять слева направо белые клетки из верхней строки и т.д. до тех
пор, пока не разложим все синие карточки. На оставшиеся клетки разложим зелёные карточки. Покажем, что никакие
зелёные карточки не могут оказаться рядом (для красных и синих карточек это очевидно). Поскольку красных и синих
карточек вместе не менее
штук, а в строке лежит не более пяти карточек каждого из этих цветов, количество строк,
занимаемых красными карточками, и количество строк, занимаемых красными карточками, вместе не меньше
Поэтому есть
строка, которая целиком заполнена красными и синими карточками. Но тогда зелёные карточки над этой строкой лежат на
белых клетках (и значит, не рядом), а зелёные карточки под этой строкой лежат на чёрных клетках(и значит, тоже не
рядом).
Ошибка.
Попробуйте повторить позже
В стране некоторые математики знакомы между собой и при любом разбиении математиков на две непустые группы найдутся двое
знакомых из разных групп. Известно, что если посадить за круглый стол любой набор из или более математиков так, чтобы любые два
соседа были знакомы, то за столом найдутся двое знакомых, не сидящих рядом. Обозначим через
количество наборов из
попарно
знакомых математиков. Докажите, что
Источники:
Рассмотрим граф знакомств математиков. По условию этот граф хордовый, т.е. в нем любой цикл из или более вершин содержит хорду
(пару смежных вершин, не соседних в цикле). Докажем, что для хордового графа
выражение
где
—
количество клик (полных подграфов) в
на
вершинах, равно числу
компонент связности графа
Предположим, что это не так, и рассмотрим в качестве наименьший по числу вершин контрпример. Ясно, что граф
содержит
больше одной вершины и связен (иначе одна из компонент связности была бы меньшим контрпримером). Удалим из графа
произвольную вершину
пусть новый граф
распался на компоненты
Пусть
,
— подграфы в
соответственно на соседях вершины
Несложно видеть, что
где слагаемое соответствует клике
слагаемые
— кликам, не содержащим
слагаемые —
— кликам, содержащим
(при удалении из них вершины
меняется четность, а стало быть, знак в выражении для
). В силу минимальности
контрпримера
Проверим, что
при всех
Предположим противное, тогда вершины одного
из графов
можно разбить на два непустых подмножества
так, что ни одно ребро не ведет из
в
Рассмотрим наименьший по числу ребер путь
из
в
в графе
Тогда цикл
не имеет хорды в графе
Мы проверили, что при всех
Тогда по формуле
т. е. граф
оказался неконтрпримером.
Ошибка.
Попробуйте повторить позже
Ученики школы посещают кружков. В каждый кружок ходит ровно
детей. Докажите, что можно рассадить всех учеников школы
по
кабинетам так, чтобы в каждом кабинете был хотя бы один представитель каждого кружка (
и
— натуральные
числа).
Источники:
Выберем учеников из первого кружка, рассадим их в разные кабинеты. Выберем
других человек из второго кружка и рассадим их, и
так далее.
Рассмотрим комнат, где число
определим позже. Посадим каждого школьника в одну из этих комнат, выбирая ее случайно (все
комнаты равновероятны). Назовем комнату подозрительной, если в ней оказались представители не всех кружков. Предположим, что
случилась УДАЧА: оказалось не более чем
подозрительных комнат. Тогда имеется
неподозрительных комнат, мы можем назвать их
кабинетами, и искомая рассадка найдена. УДАЧА заведомо иногда случается, если математическое ожидание
числа
подозрительных комнат меньше
Заметим, что
равно количеству комнат
умноженному на вероятность
того, что конкретная комната подозрительна. Эта вероятность, в свою очередь, не превосходит
Итак,
если
то при таком требуемая рассадка существует. Уже при
получается экспоненциальное по
выражение, наилучшего
результата — около
— можно добиться при
Ошибка.
Попробуйте повторить позже
В стране городов, каждые два города соединены (двусторонними) авиалиниями, цены всех перелетов попарно различны (для любой
пары городов цена перелета «туда» равна цене «обратно»). В каждом городе находится турист. Каждый вечер все туристы переезжают:
богатые туристы — по самой дорогой, бедные — по самой дешевой линии, ведущей из соответствующего города. Через
дней оказалось,
что в каждом городе снова по одному туристу. За это время ни один турист не посетил никакой город дважды. При каком наибольшем
такое возможно?
Источники:
Ясно, что во время путешествий никакие два богатых туриста (или два бедных) не могли оказаться в одном городе. С другой стороны, условие задачи не запрещает находиться в одном городе одновременно бедному и богатому туристу, важно лишь, чтобы в начальный и в конечный момент в каждом городе было по одному туристу.
Допустим, что среди туристов имеется (или более) «богачей». Нарисуем граф: вершины — это города, из каждого города проведем
самый дорогой выходящий путь. Тогда этот граф представляет собой лес, в каждом дереве которого все ребра направлены к корню,
за исключением единственного ребра, выходящего из корня, — это ребро в дереве как бы двустороннее. Возьмем богача,
который расположен ближе всего к корню своего дерева. Этот богач будет в течение
ходов самым близким к корню.
Значит, он проедет по городам, в которых еще не было других богачей. Это может быть только если граф — это путь из
вершин, богачи занимают первые
вершин этого пути (т. е. половину) и гуськом движутся по этому пути в сторону второй
половины. Отсюда следует, что богачей не может быть больше
а также что количество переездов тоже не превосходит
Тогда бедных туристов тоже и они двигаются по аналогичному «бедному» пути, причем в начальный момент они занимают всю
вторую половину «богатого» пути. Эти пути не имеют общих звеньев, и при этом движение бедняков таково, что с каждым ходом они
должны освобождать от своего присутствия очередную вершину второй половины богатого пути, смещаясь гуськом в первую половину.
Тогда движение туристов может происходить, например, следующим образом.
Обозначим города Допустим, что путь
составлен из самых дорогих авиалиний, для определенности пусть цена перелета равна
рублей. А «бедный путь»
пусть сначала проходит по городам с большими четными номерами, потом — по городам с большими нечетными, а далее — с малыми:
сначала с четными, потом с нечетными:
Цены этих авиалинии пусть убывают от до
рубля при движении вдоль этого пути. Цены остальных авиалиний назначим
произвольно в диапазоне от
до
рублей.
При
Ошибка.
Попробуйте повторить позже
Ладья, стоящая на поверхности клетчатого куба, бьёт клетки, находящиеся с той клеткой, где она стоит, в одном ряду, а также на
продолжениях этого ряда через одно или даже несколько ребёр. (На картинке показан пример для куба видимые клетки,
которые бьёт ладья, закрашены серым).
![]()
Какое наибольшее количество не бьющих друг друга ладей можно расставить на поверхности куба
Источники:
Оценка
Назовем ободком множество клеток, находящихся в одном ряду, а также на продолжении этого ряда за одно или несколько ребер. Каждая
ладья держит под боем клетки двух ободков. Всего на поверхности куба имеется ободков (есть три возможных направления, по
ободков в каждом). На каждом ободке может стоять не более одной ладьи, и любая ладья стоит на двух ободках. Поэтому ладей не может
быть больше
Пример
Рассмотрим три соседние грани и поделим каждую на квадрата
. Далее в трех квадратах, указанных на рисунке, поставим ладьи
на одной из главных диагоналей.
![]()
ладей
Ошибка.
Попробуйте повторить позже
В межгалактической империи планет, любые две из которых соединены двусторонней прямой космической линией. Этими линиями
владеют
транспортных компаний. Император хочет закрыть
компаний так, чтобы, пользуясь только рейсами оставшихся, можно
было бы с любой планеты добраться до любой другой. При каком наибольшем
он гарантированно сможет осуществить свой
план?
Покажем сначала, что всегда найдутся компаний, с помощью которых можно добраться от любой планеты до любой другой. Выберем
произвольно
компаний, назовем их стремительными, а остальные — надежными. Предположим, что посредством стремительных
компаний нельзя добраться, скажем, с Венеры на Сатурн. Это значит, что Венеру и Сатурн соединяет рейс надежной компании, и любая
другая планета соединена рейсом надежной компании либо с Венерой, либо с Сатурном. Отсюда следует, что с любой планеты до
любой можно добраться рейсами надежных компаний (через Венеру и Сатурн). Добавляя к надежным компаниям любую
стремительную, получаем требуемые
компаний. Теперь приведем пример, показывающий, что
компаний
закрыть с выполнением требований удастся не всегда. Для каждого множества
из 1008 авиакомпаний может найтись
такая планета
на которую летают только компании из
Планет для выполнения такого требования нужно не
более чем
(общее число подмножеств множества компаний), а у нас их больше. При этом для любых двух планет
их можно соединить рейсом компании из
— это множество непусто. Как соединяются другие пары планет,
неважно.Теперь при закрытии любого множества
из
компаний планета
становится изолирована от остальной
галактики.
Ошибка.
Попробуйте повторить позже
В стране Центумии некоторые пары городов соединены дорогами, причем из каждого города выходит ровно дорог.
Пучком называется набор из
дорог, выходящих из одного города. Докажите, что все дороги можно разбить на несколько
пучков.
Источники:
Рассмотрим граф , в котором вершины — это города, а рёбра — дороги. Степени всех вершин этого графа равны
Разобьем все рёбра
графа
на реберно непересекающиеся циклы. В каждом цикле зададим произвольно порядок обхода и ориентируем
рёбра в направлении обхода цикла. Тогда в каждую вершину
входит
ребер и из каждой вершины выходит тоже
ребер. Разобьем все ребра, выходящие из каждой вершины, на 5 пучков. Тогда все рёбра графа
разобьются на
пучки.
Ошибка.
Попробуйте повторить позже
Набор разновесов содержит по одной гире каждого из весов граммов. Для натурального
докажите, что количество
способов набрать этими гирями
граммов не больше, чем количество способов набрать
грамм.
Источники:
Пусть имеется способов выбрать
граммов без использования гири в
г и
способов набрать
граммов с использованием гири
в
г.
Добавив к каждому из способов первой группы гирю в г, мы получим суммарный вес
граммов. Значит,
(способов
выбрать
граммов без единицы может быть равно нулю, поэтому знак больше или равно).
С другой стороны, если для каждого способа набрать граммов с использованием гири в
г мы уберём эту гирю и заменим самую
большую использованную гирю в этом способе на ту, которая весит на
г больше, снова получится суммарный вес
граммов.
Следовательно, (при нечётном
появляется ещё один способ взять гири вне этого алгоритма, поэтому знак больше или
равно).
Сложив полученные два неравенства, имеем требуемое.



