Ошибка.
Попробуйте повторить позже
Даны векторы и
Найдите скалярное произведение векторов
и
Скалярное произведение двух векторов и
равно
Следовательно, скалярное произведение наших векторов равно
Ошибка.
Попробуйте повторить позже
Даны векторы и
Найдите скалярное произведение векторов
и
Скалярное произведение двух векторов и
равно
Следовательно, скалярное произведение векторов и
равно
Ошибка.
Попробуйте повторить позже
Найдите скалярное произведение векторов и
Скалярное произведение векторов с координатами и
равно
Тогда искомое скалярное произведение равно
Ошибка.
Попробуйте повторить позже
Найдите скалярное произведение и
Скалярное произведение векторов с координатами и
равно
В данной задаче
Ошибка.
Попробуйте повторить позже
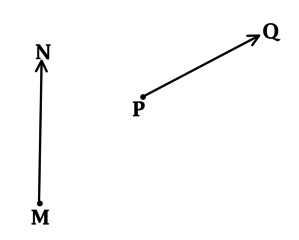
На координатной плоскости изображены векторы и
Найдите скалярное
произведение
Если и
— точки на координатной плоскости, то вектор
имеет координаты
Найдем координаты векторов и
Скалярное произведение двух векторов и
равно
Следовательно, скалярное произведение векторов и
равно
Ошибка.
Попробуйте повторить позже
На координатной плоскости изображены векторы и
Найдите скалярное
произведение
Источники:
Если и
— точки на координатной плоскости, то вектор
имеет координаты
Найдем координаты векторов и
Скалярное произведение векторов и
равно
Следовательно, скалярное произведение векторов и
равно
Ошибка.
Попробуйте повторить позже
На координатной плоскости изображены векторы и
Найдите скалярное
произведение этих векторов.
Как известно, если и
— точки на координатной плоскости, то
вектор
имеет координаты
Найдем координаты векторов
и
Скалярное произведение двух векторов и
равно
Следовательно, скалярное произведение векторов и
равно
Ошибка.
Попробуйте повторить позже
Даны векторы и
Найдите угол между векторами
и
Ответ
дайте в градусах.
Скалярное произведение двух векторов и
равно
Здесь — длина вектора
— угол между векторами
и
Найдем длины векторов и
С другой стороны, скалярное произведение двух векторов и
равно
То есть в нашем случае
Таким образом, получаем уравнение
Так как то
Ошибка.
Попробуйте повторить позже
На рисунке изображены векторы и
Найдите косинус угла между ними.
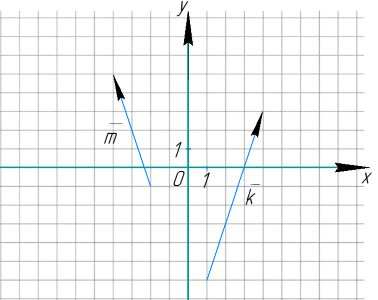
Запишем координаты векторов и
По определению скалярное
произведение двух векторов равно произведению их длин на косинус угла между
ними. Косинус угла между векторами равен
Найдем скалярное произведение
Найдем длины векторов:
Тогда
Ошибка.
Попробуйте повторить позже
На координатной плоскости изображены векторы и
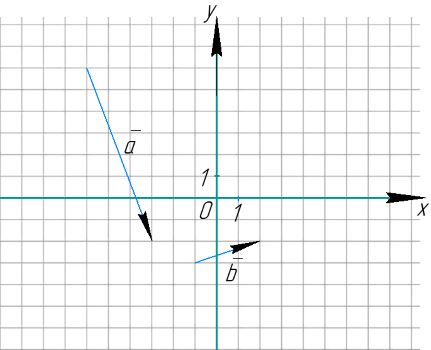
Найдите скалярное произведение векторов и
Запишем координаты векторов
Координаты вектора
Скалярное произведение равно
Ошибка.
Попробуйте повторить позже
Даны векторы
и
Найдите
, если
Найдем координаты вектора
Тогда
Решая уравнение, находим
Ошибка.
Попробуйте повторить позже
На координатной плоскости даны точки
и
Известно, что
— прямоугольный с прямым углом
Найдите
Если то скалярное произведение
Имеем
Ошибка.
Попробуйте повторить позже
На координатной плоскости даны точки
и
Найдите ординату точки
пересечения диагоналей четырехугольника
Докажем, что Это будет верно, если скалярное произведение
Заметим, что Следовательно,
и
Следовательно,
— прямоугольник. Значит,
— середина
Следовательно,
Следовательно, ордината точки пересечения диагоналей равна -1,5.
Ошибка.
Попробуйте повторить позже
На координатной плоскости даны точки
и
Известно, что
— прямоугольник. Найдите
Проверим, что Тогда скалярное произведение
Так как — прямоугольник, то
и
следовательно,
Тогда
Ошибка.
Попробуйте повторить позже
Дано уравнение окружности и точка
лежащая на этой
окружности. Если
— центр окружности,
— координатный вектор, то
найдите скалярное произведение
и
Так как лежит на окружности, то координаты точки
удовлетворяют
уравнению окружности. Следовательно,
Следовательно, Координаты центра окружности находятся из
уравнения:
Следовательно,
Так как то угол наклона вектора
к положительному
направлению оси абсцисс равен
то есть угол между
и
равен
Следовательно,
Ошибка.
Попробуйте повторить позже
Дан четырехугольник На сторонах
и
отмечены точки
и
соответственно так, что
Точки
и
— середины отрезков
и
соответственно. Длина отрезка
Найдите скалярное произведение
Рассмотрим чертеж
Заметим, что
Пусть
Тогда
Следовательно,
Таким образом, векторы
и
коллинеарны, то есть точки
и
лежат на одной прямой. Следовательно, из разложений
этих векторов по векторам
и
следует, что
Следовательно,
Ошибка.
Попробуйте повторить позже
— четырехугольник со стороной
— такая точка внутри этого
четырехугольника, что
Найдите скалярное произведение
векторов
и
Рассмотрим чертеж
Из равенства векторов
следует, что 1) отрезки
и
пересекаются в точке
2)
— середина этих отрезков. Из этого
следует, что
— параллелограмм. Следовательно,
Следовательно,
Ошибка.
Попробуйте повторить позже
На координатной плоскости изображен прямоугольный равнобедренный
треугольник причем точки
и
лежат на осях координат. Найдите
косинус острого угла между медианами, проведенными к катетам этого
прямоугольного треугольника.
Пусть и
лежат на осях
и
соответственно, а
— начало
координат. Рассмотрим векторы
где
и
—
медианы, проведенные к катетам. Тогда
Причем
Тогда
Обозначим Тогда скалярное произведение векторов
и
можно записать двумя способами:
Ошибка.
Попробуйте повторить позже
На координатных осях от начала координат отложены векторы и
и на них,
как на катетах, построен прямоугольный треугольник, в котором
—
вектор высоты этого треугольника к гипотенузе. Найдите длину вектора
Пусть
то есть длины векторов
и
равны
и
соответственно. Тогда нужно найти
Рассмотрим рисунок:
Получаем такой прямоугольный треугольник, построенный на векторах
и
По условию
Вспомним, что дает перпендикулярность векторов для их скалярного
произведения. Два вектора и
перпендикулярны тогда и
только тогда, когда их скалярное произведение равно нулю:
Так как то имеем
Следовательно,
Из планиметрии известна формула (произведение катетов равно произведению гипотенузы на проведенную к ней высоту)
Воспользуемся ей:
Ошибка.
Попробуйте повторить позже
Даны три неколлинеарных вектора
и
Известно, что длины
векторов
и
равны. Найдите отношение
Рассмотрим это отношение:
Но по условию, следовательно, числитель полученной дроби равен
знаменателю. Следовательно, дробь равна



