Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы один корень.
Перепишем уравнение в виде
Рассмотрим две функции и
и исследуем их.
является композицией двух функций:
и
. Так как
возрастает
,
убывает при
и возрастает при
, то при
убывает, а при
возрастает.
при любом варианте раскрытия двух модулей представляет из себя линейную функцию, причем характер ее монотонности зависит от того, как раскроется первый модуль. Действительно, если он раскроется отрицательно, то
, то есть коэффициент перед
будет положительный, следовательно, функция возрастает. При положительном раскрытии модуля получим
, то есть отрицательный коэффициент перед
, следовательно, функция убывает. Подытожим: при
функция возрастает, при
убывает.
Нам требуется, чтобы графики функций и
имели хотя бы одну точку пересечения, что схематично выглядит следующим
образом:
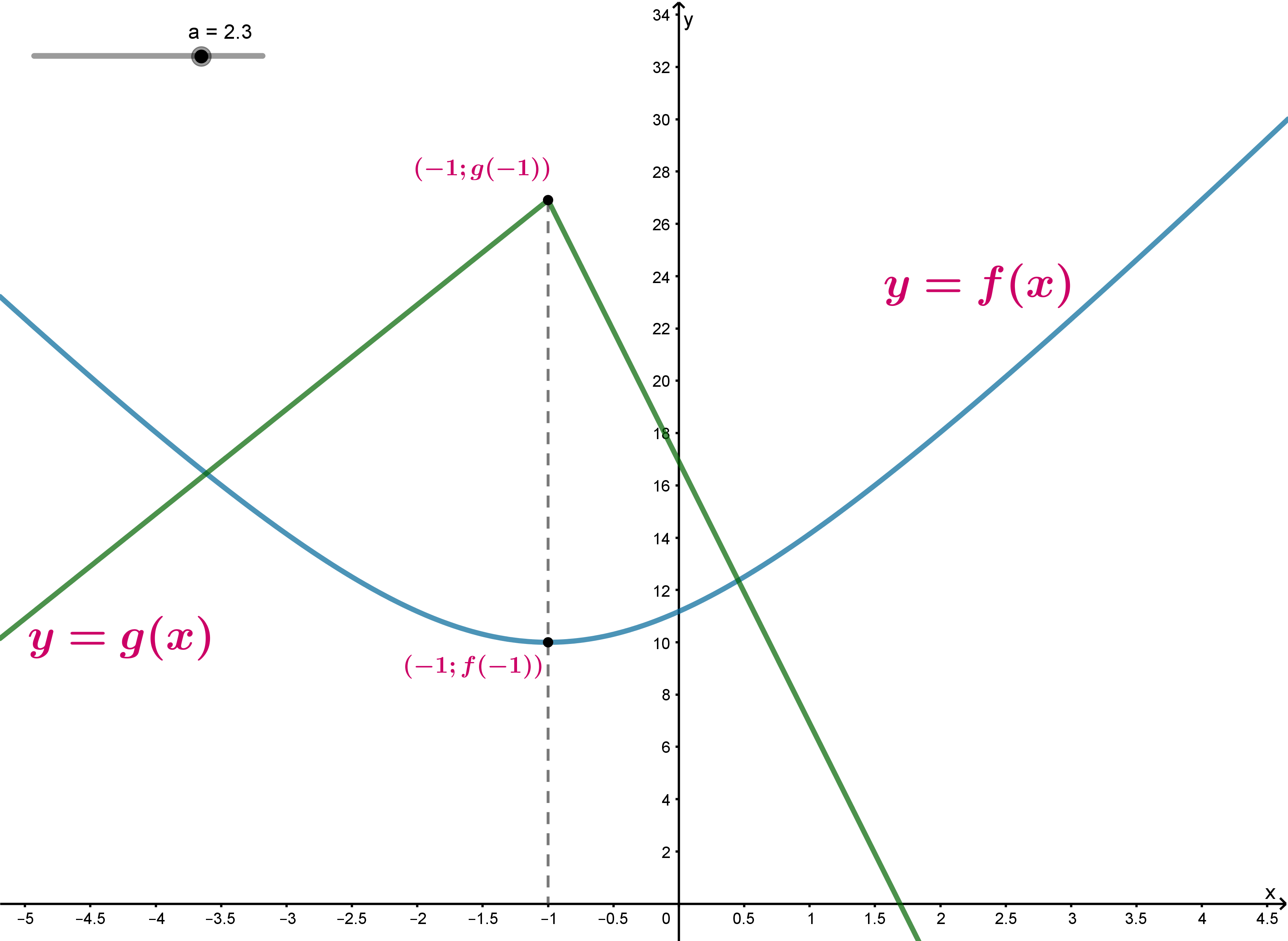
Это задается условием:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы один корень.
Рассмотрим уравнение в виде
Характер монотонности функции зависит от того, как раскроется первый модуль. Действительно, при
он раскроется
отрицательно, и функция будет иметь вид
, где
принимает одно из значений
, то
есть
, значит, функция убывает. При
имеем
, где
, то есть
, следовательно, функция возрастает. Таким образом, чтобы уравнение
имело хотя бы одно решение, то есть
график ункции имел хотя бы одну точку пересечения с осью абсцисс, нужно, чтобы график выглядел схематично так:
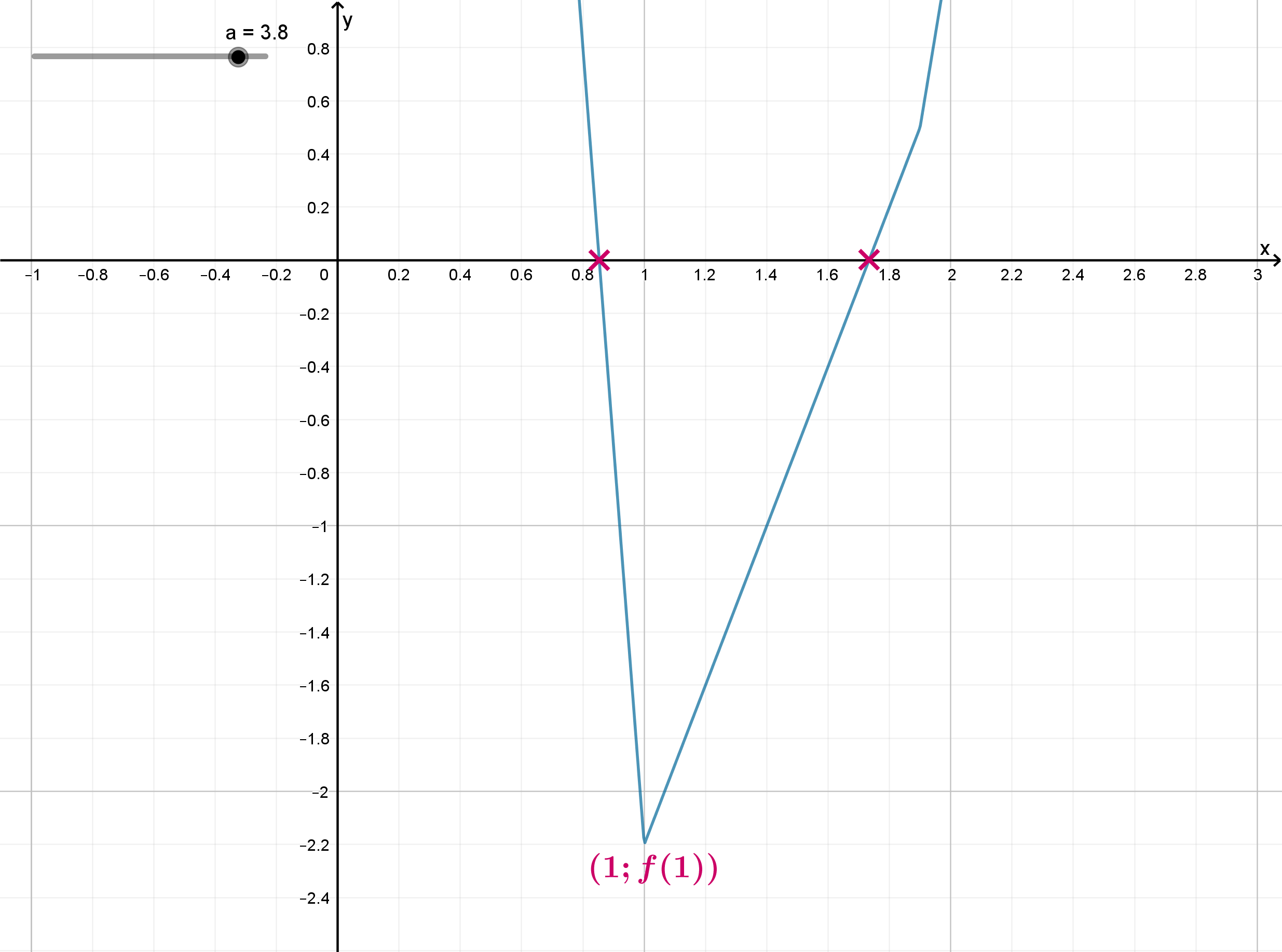
То есть необходимо, чтобы
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых неравенство
выполняется для всех .
Перепишем неравенство в виде:
Рассмотрим две функции и
и исследуем их.
является суммой двух возрастающих функций, следовательно, сама является возрастающей функцией.
при любом варианте раскрытия двух модулей убывает, так как принимает вид
, где
может принимать одно из значений
.
Тогда на одной координатной плоскости графики схематично выглядят так:
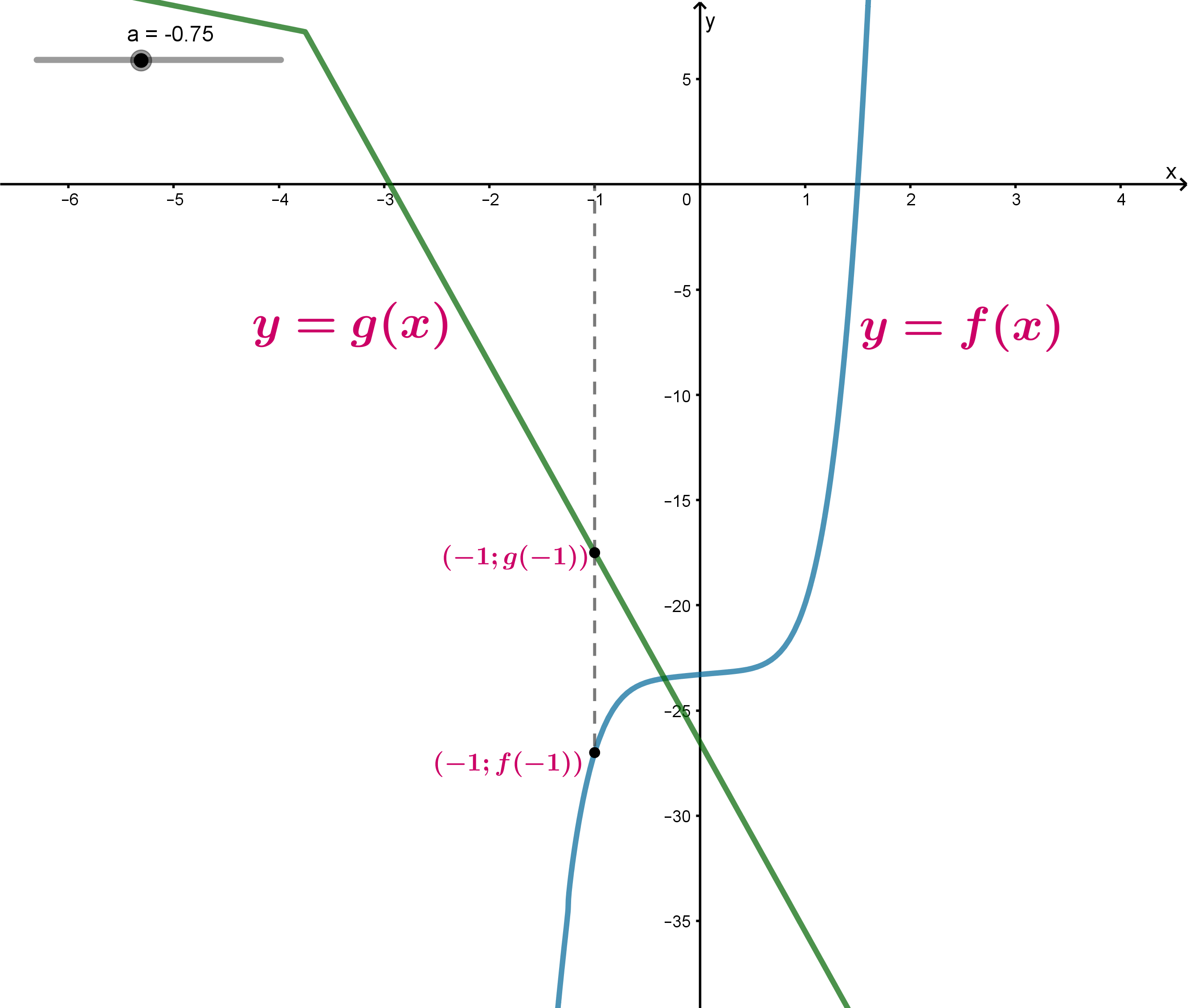
То есть графики функций (где одна возрастает, а другая убывает) имеют не более одной точки пересечения, а в нашем случае — ровно одну.
Если обозначить ее за , то решением неравенства
будут
.
Чтобы отрезок содержался во множестве решений неравенства, необходимо, чтобы
, или, что то же
самое,
Ошибка.
Попробуйте повторить позже
Найдите , при которых уравнение
имеет хотя бы один корень.
Перепишем уравнение в виде
Рассмотрим две функции и
и исследуем их.
является композицией двух функций:
и
. Так как
возрастает
,
убывает при
и возрастает при
, то при
убывает, а при
возрастает.
при любом варианте раскрытия двух модулей представляет из себя линейную функцию, причем характер ее монотонности зависит от того, как раскроется первый модуль. Действительно, если он раскроется отрицательно, то
, то есть коэффициент перед
будет положительный, следовательно, функция возрастает. При положительном раскрытии модуля получим
, то есть отрицательный коэффициент перед
, следовательно, функция убывает. Подытожим: при
функция возрастает, при
убывает.
Нам требуется, чтобы графики функций и
имели хотя бы одну точку пересечения, что схематично выглядит следующим
образом:
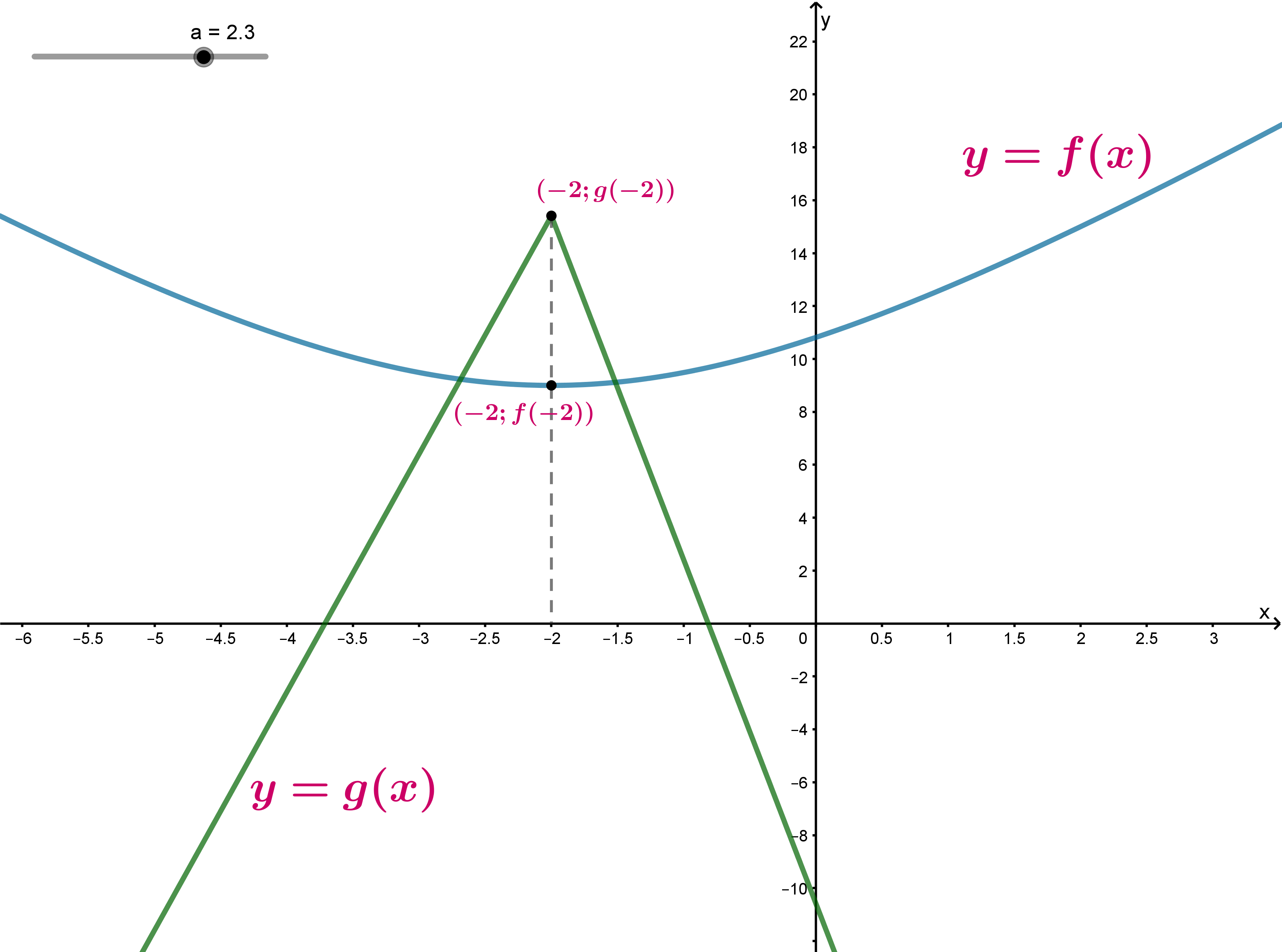
Это задается условием:
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра при которых уравнение
имеет хотя бы одно решение.
Преобразуем левую часть уравнения:
Пусть Тогда графиком функции
является парабола с вершиной в точке
и ветвями,
направленными вниз. Это означает, что в точке
функция
принимает наибольшее из возможных значений, то есть
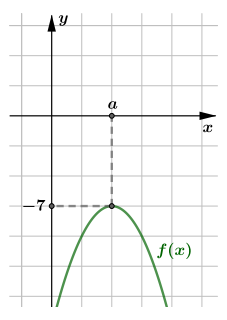
Рассмотрим правую часть уравнения. Пусть Воспользуемся принципом главного модуля, так как
только раскрытие первого модуля определяет, будет функция возрастать или убывать. Раскроем модули в функции
чтобы
убедиться в этом:
- Если
то при раскрытии первого модуля коэффициент при
будет равен
Заметим, что, как бы ни был раскрыт второй модуль, итоговый коэффициент при
будет отрицательным. Тогда на промежутке
функция
будет убывать.
- Если
то при раскрытии первого модуля коэффициент при
будет равен 6. Заметим, что, как бы ни был раскрыт второй модуль, итоговый коэффициент при
будет положительным. Тогда на промежутке
функция
будет возрастать.
Следовательно, в точке функция
будет принимать наименьшее из возможных значений, то есть
Нас просят найти такие значения параметра при которых исходное уравение будет иметь хотя бы одно решение. То есть
графики функций
и
должны иметь хотя бы одну точку пересечения. Заметим, что в точке
функция
принимает свое наибольшее значение, а функция
— наименьшее. Тогда если
то графики функций
и
вовсе не будут пересекаться.
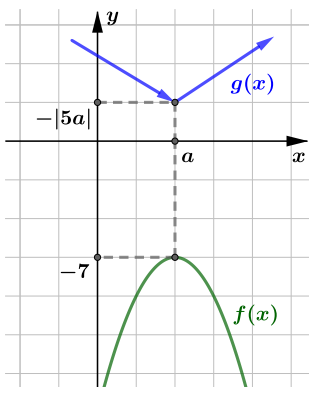
Следовательно, если у уравнения есть хотя бы один корень, то то есть
Заметим, что условия достаточно для того, чтобы исходное уравнение имело хотя бы одно решение, так как
принимает любое значение от
до
поэтому
примет значение, меньшее
а значит пересечет
график
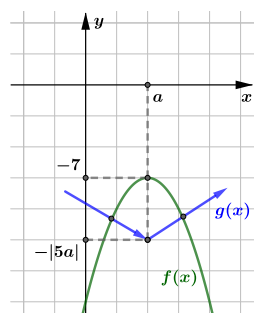
Следовательно, исходное уравнение имеет хотя бы одно решение при
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 4 |
| Недостаточное обоснование либо в ходе рассмотрения функций, либо при решении неравенства | 3 |
| Обоснованный переход к неравенству, но его решение неверное | 2 |
| Введены и рассмотрены функции левой и правой части (аналитически или графически) | 1 |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 4 |
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых уравнение
имеет более одного корня.
Перепишем уравнение в другом виде:
Пусть
Изобразим графики обеих функций:
1)
и
– точки минимума,
– точка максимума.
Причем
2)
Рассмотрим два случая:
2.1) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
,
– линейная функция, коэффициент перед
у которой будет отрицательным (в
точности, он будет равен
или
). Т.е.
всегда убывает при
.
2.2) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
,
– линейная функция, коэффициент перед
у которой будет положительным (в
точности, он будет равен
или
). Т.е.
всегда возрастает при
.
Таким образом, – точка максимума (единственная) у функции
, причем
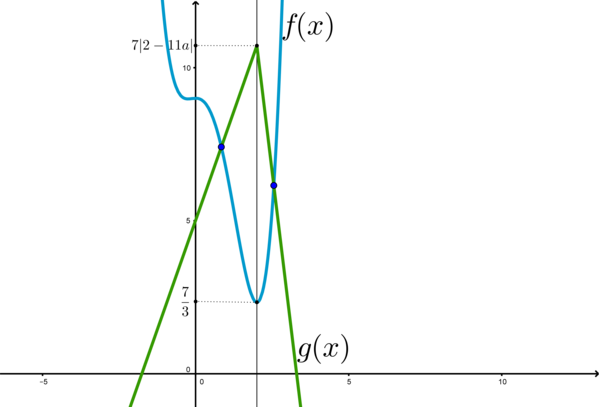
Уравнение будет иметь более одного корня, если .
Решая данное неравенство, получим .
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых уравнение
имеет решения.
Сделаем замену: . Для того, чтобы исходное уравнение имело хотя бы одно решение,
необходимо и достаточно, чтобы полученное уравнение
1 способ.
1) . Модули раскрываются следующим образом:
Изобразим схематично график системы
Из графика видно, что уравнение ни при каких
2) . Тогда уравнение примет вид
3) . Тогда модули раскрываются следующим образом:
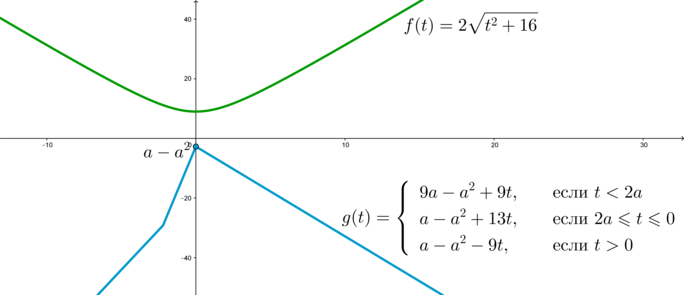
Изобразим схематично график системы
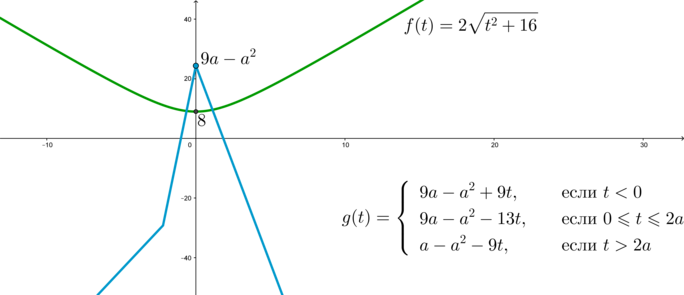
Уравнение будет иметь хотя бы один корень, когда вершина графика функции
2 способ.
Рассмотрим два случая:
1) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
,
справа будет стоять линейная функция, коэффициент перед
у которой будет отрицательным
(в точности, он будет равен или
, или
). То есть функция справа будет всегда
убывать.
2) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
, справа будет стоять линейная функция, коэффициент перед
у которой будет
положительным (в точности, он будет равен или
, или
). То есть функция справа будет всегда
возрастать.
Таким образом, точка максимума у функции справа – это , и в этой точке значение функции
равно
.
Рассмотрим функцию слева: она всегда положительна, имеет единственный минимум в точке
, и в этой точке значение функции равно
(до точки
она убывает, после –
возрастает).
Следовательно, уравнение будет иметь решения в том случае, если
Ошибка.
Попробуйте повторить позже
Найдите все значения , при каждом из которых уравнение
имеет хотя бы один корень.
Перепишем уравнение в виде
Функция
Функция
Действительно, при
Найдем значение
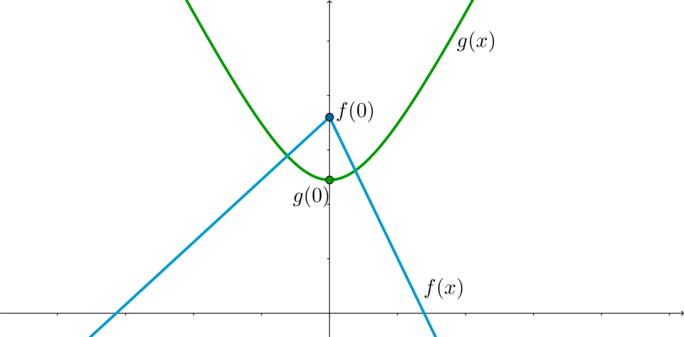
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при каждом из которых уравнение
имеет хотя бы один корень.
Рассмотрим две функции: и
.
Заметим, что при всех
и
(как сумма модулей). Следовательно, для того, чтобы графики
функции имели точки пересечения, нужно, чтобы
, то есть
.
Заметим, что если третий модуль раскроется с плюсом, то, вне зависимости от того, как раскроются
первые два модуля, слева будет стоять либо возрастающая функция (,
, причем
будет равно либо 4, либо 2), либо константа (когда
).
Если третий модуль раскроется с минусом, то, также вне зависимости от того, как раскроются первые
два модуля, слева будет убывающая функция (,
, причем
будет равно либо
, либо
) или константа (когда
).
При третий модуль раскроется с минусом, при
– с плюсом.
Заметим, что так как , то
.
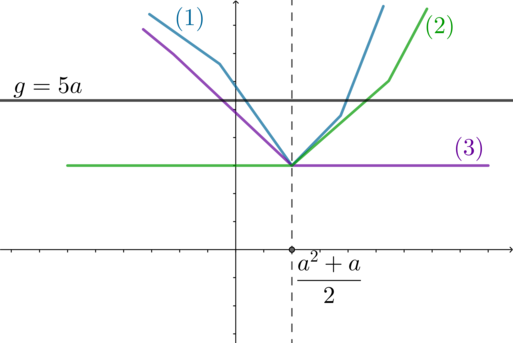
Значит, функция будет либо константой (ее график
будет параллелен оси абсцисс), либо ее график будет иметь один из трех видов:
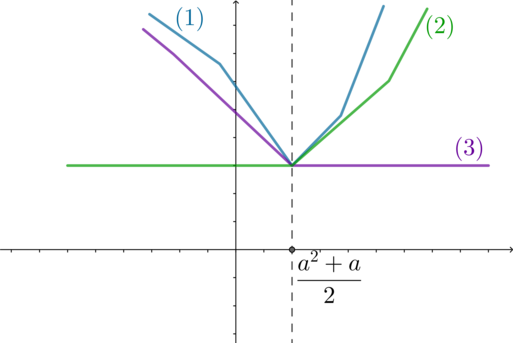
Графиком функции при каждом фиксированном
будет прямая, параллельная
оси абсцисс. Следовательно, для того, чтобы графики
и
имели хотя бы одну точку
пересечения, нужно, чтобы график
находился не ниже вершины
графика
:
Ошибка.
Попробуйте повторить позже
Найдите все значения , при каждом из которых уравнение
имеет хотя бы один корень.
Перепишем уравнение в виде
Функция
Функция
Действительно, при
Найдем значение
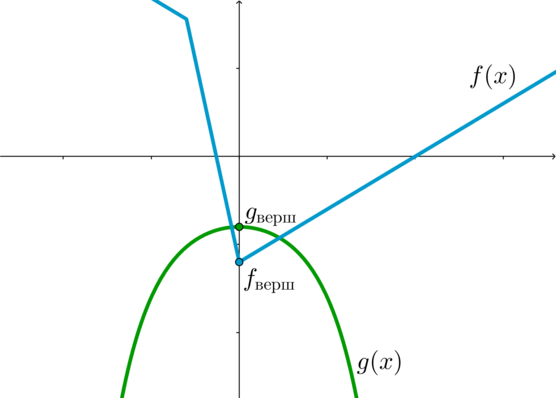
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых уравнение
имеет решения.
Сделаем замену: . Для того, чтобы исходное уравнение имело хотя бы одно решение,
необходимо и достаточно, чтобы полученное уравнение
1 способ.
1) . Модули раскрываются следующим образом:
Изобразим схематично график системы , причем заметим, что при
:

Из графика видно, что уравнение ни при каких не имеет решений.
2) . Тогда уравнение примет вид
3) . Тогда модули раскрываются следующим образом:
Изобразим схематично график системы , причем заметим, что при
:
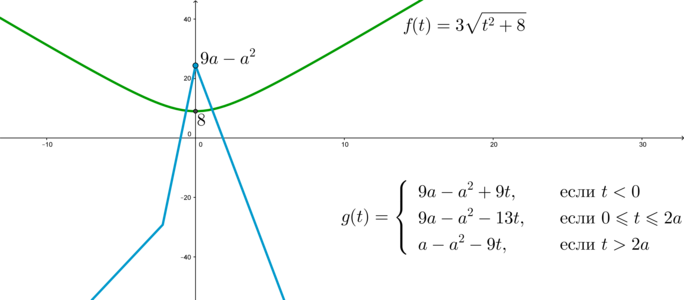
Уравнение будет иметь хотя бы один корень, когда вершины графика функции будет не ниже
вершины графика функции
:
2 способ.
Рассмотрим два случая:
1) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
,
справа будет стоять линейная функция, коэффициент перед
у которой будет отрицательным
(в точности, он будет равен или
, или
). То есть функция справа будет всегда
убывать.
2) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
, справа будет стоять линейная функция, коэффициент перед
у которой будет
положительным (в точности, он будет равен или
, или
). То есть функция справа будет всегда
возрастать.
Таким образом, точка максимума у функции справа – это , и в этой точке значение функции
равно
.
Рассмотрим функцию слева: она всегда положительна, имеет единственный минимум в точке
, и в этой точке значение функции равно
(до точки
она убывает, после –
возрастает).
Следовательно, уравнение будет иметь решения в том случае, если
Решая данное неравенство, получаем тот же ответ
Ошибка.
Попробуйте повторить позже
Найдите все значения параметра , при которых уравнение
имеет более одного корня.
Перепишем уравнение в другом виде:
Пусть
Изобразим графики обеих функций:
1)
и
– точки минимума,
– точка максимума.
Причем
2)
Рассмотрим два случая:
2.1) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
,
– линейная функция, коэффициент перед
у которой будет отрицательным (в
точности, он будет равен
или
). Т.е.
всегда убывает при
.
2.2) . Тогда
. В этом случае вне зависимости от того, как раскроется модуль
,
– линейная функция, коэффициент перед
у которой будет положительным (в
точности, он будет равен
или
). Т.е.
всегда возрастает при
.
Таким образом, – точка максимума (единственная) у функции
, причем
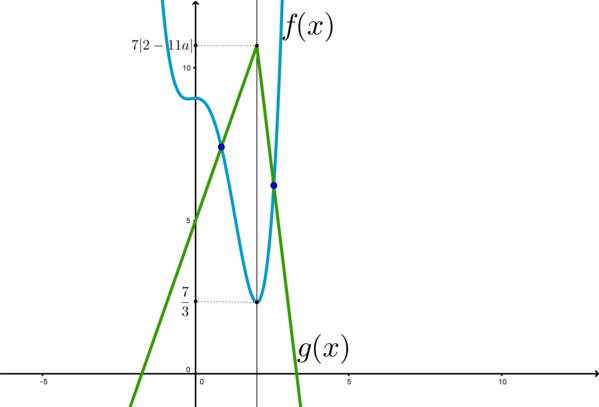
Уравнение будет иметь более одного корня, если .
Решая данное неравенство, получим .
.



