Ошибка.
Попробуйте повторить позже
В треугольнике проведена медиана
Точка
— середина отрезка
точка
— пересечение прямой
и стороны
Известно, что
Докажите, что
Первое решение.
Пусть — точка, симметричная точке
относительно
Тогда
и
— параллелограмм (так как диагонали
четырехугольника
делят друг друга пополам).
![]()
В треугольнике стороны
и
равны, следовательно,
Кроме того,
как вертикальные,
как накрест лежащие при параллельных прямых
и
и секущей
Треугольники и
равны по углу
и прилежащим к нему сторонам
следовательно,
Итого, получили следующую цепочку равенств углов
Тогда в треугольнике углы при вершинах
и
равны и
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Задачу можно решить без удвоения медианы, если обратить внимание на треугольники и
В этих треугольниках углы и
равны как дополняющие равные по условию углы
и
до развернутого
угла. Кроме того,
и
по условию.
Тогда треугольники и
равны по двум сторонам и углу между ними.
Отсюда лежащие напротив равных сторон углы и
равны и с привлечением равных вертикальных углов
и
получаем равные углы в треугольнике
и требуемое равенство
Ошибка.
Попробуйте повторить позже
На отрезке выбраны точки
и
. На отрезках
и
построены в одну сторону правильные треугольники
и
.
Докажите, что
.
По условию — равносторонние треугольники. Тогда все их углы равны
Пусть точка — симметричная точке
относительно прямой
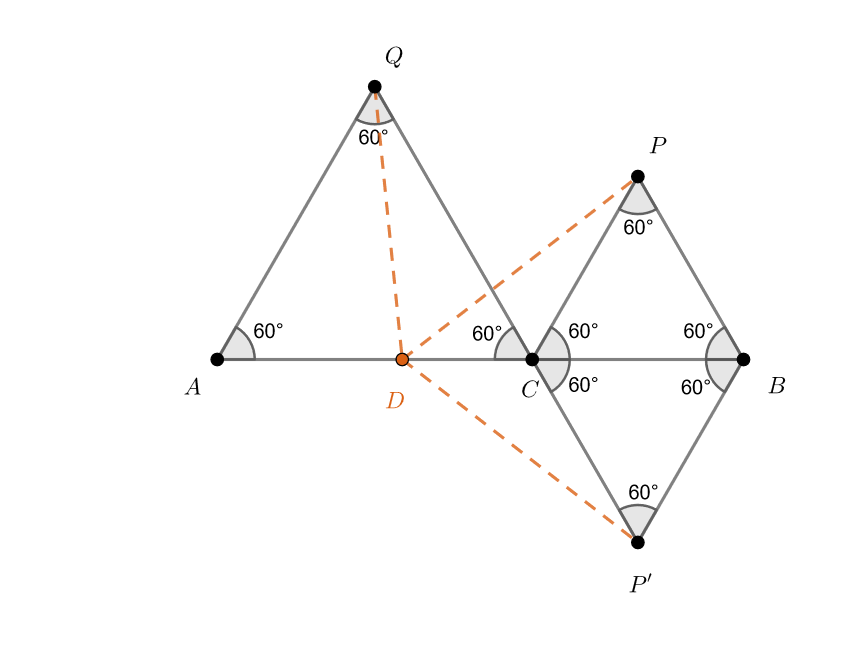
В силу симметрии Тогда
— тоже равносторонний треугольник, у которого все углы по
Заметим, что Значит, точки
лежат на одной прямой.
Из неравенства треугольника на строны
В силу симметрии Так как
— равносторонние,
Тогда
Объединим полученное выше:
Значит, действительно выполнено неравенство
Ошибка.
Попробуйте повторить позже
В трапеции
Докажите, что
Первое решение.
В силу параллельности
Отложим от точки отрезок
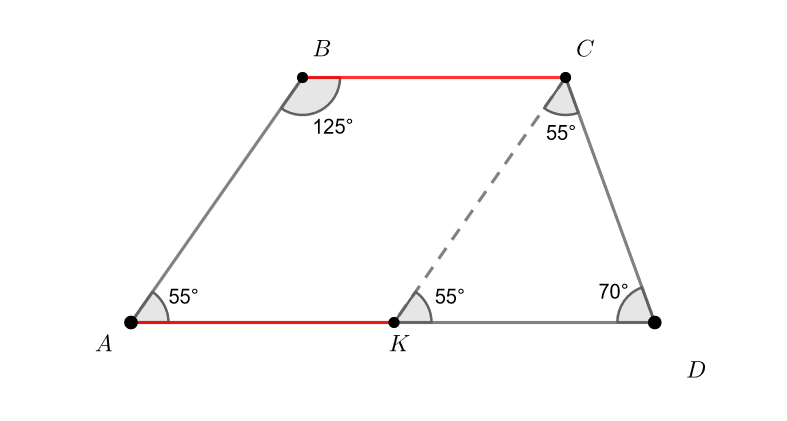
Тогда — параллелограмм (т. к.
а
Значит, как односторонние углы при секущей
.
Найдем угол
Получили, что Тогда
— равнобедренный, в котором
.
В итоге,
______________________________________________________________________________________________________________________________________________________
Второе решение.
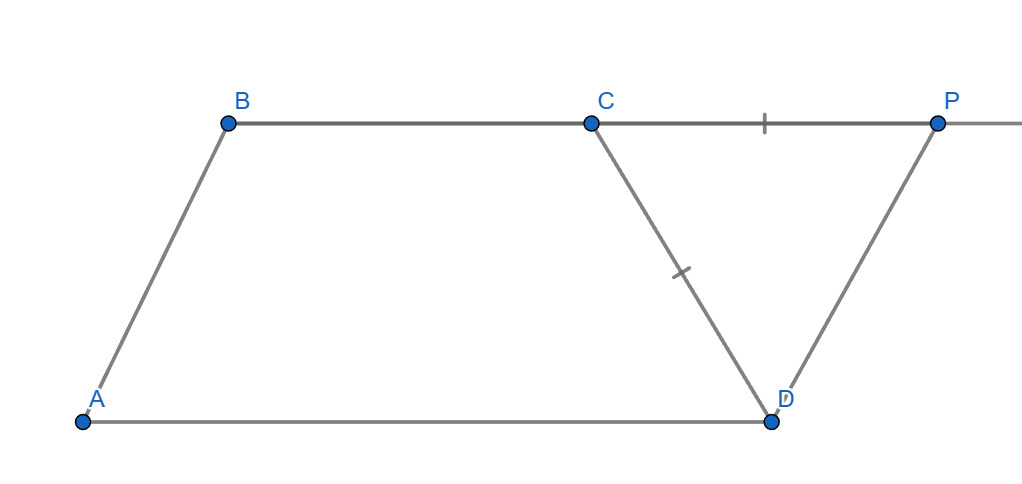
Отложим на прямой за точку
отрезок
равный
Т.к. можем получить
Треугольник равнобедренный, т.к.
поэтому
Получаем, что
Следовательно, значит,
Но мы знаем, что
поэтому
— параллелограмм.
Значит,
Ошибка.
Попробуйте повторить позже
Недалеко от прямой речки по одну сторону от неё расположены два домика и
. Вася хочет дойти от
до
, набрав по пути воды
из речки. Как нужно идти Васе, чтобы пройденный путь был кратчайшим?
Пусть — точка, симметричная
, относительно берега речки. Рассмотрим
— точку пересечения прямой
с берегом. Докажем,
что кратчайший маршрут будет ломаной
.
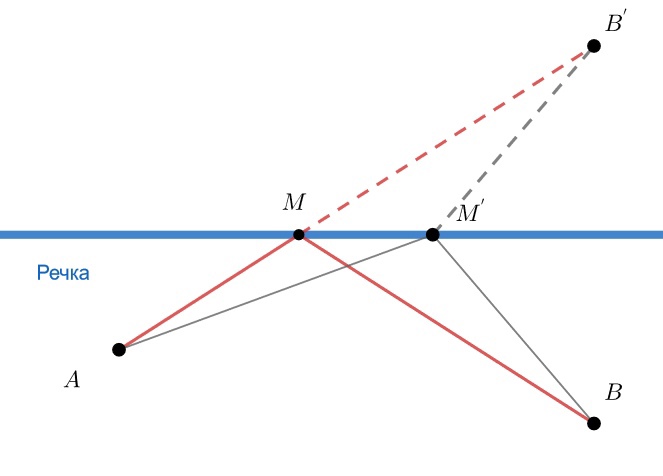
Пусть есть точка на берегу, отличная от
. В силу симметрии
,
. Длина ломаной
Применим неравенство треугольника для :
Значит, , то есть маршрут
— кратчайший.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике проведена биссектриса
На основании
отмечена такая точка
что
Биссектриса угла
пересекает сторону
в точке
Докажите, что
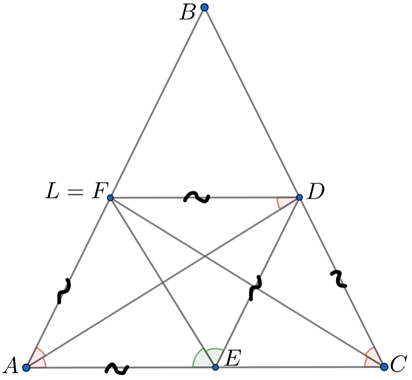
Проведем биссектрису угла
Так как треугольник
равнобедренный,
из чего полу чаем, что
треугольник
тоже является равнобедренным. Пусть
тогда
Кроме того,
откуда
В силу данной параллельности
и треугольник
равнобедренный. Таким образом, в четырехугольнике
стороны
и
равны и параллельны, следовательно,
—
параллелограмм, но
следовательно,
— ромб. По свойству ромба
является биссектрисой угла
т. е. точки
и
совпадают. Как мы уже знаем,
чтд.
Ошибка.
Попробуйте повторить позже
Биссектрисы углов и
выпуклого четырехугольника
пересекаются в точке
биссектрисы углов
и
— в точке
Докажите, что
Пусть — проекции точек
на прямую
— проекции на прямую
Легко видеть, что точка
лежит на луче
— на луче
поэтому
аналогично
Кроме того, если точка
—
проекция
на
(она лежит на отрезке
), то
Аналогично Осталось заметить, что
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
равны
На сторонах
и
выбраны точки
и
соответственно так,
что
Оказалось, что прямая
параллельна биссектрисе угла
Найдите угол
Проведём через точку прямую, параллельную
Пусть она пересечёт
в точке
Тогда
и
поэтому треугольники
и
равны по двум углам и стороне. Поэтому
и
— параллелограмм. Но тогда
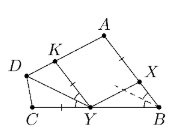
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
параллелограмма
. Точка
делит его сторону
на отрезки с длинами
и
так, что
угол
. Найдите
.
Удвоим , получим точку
.
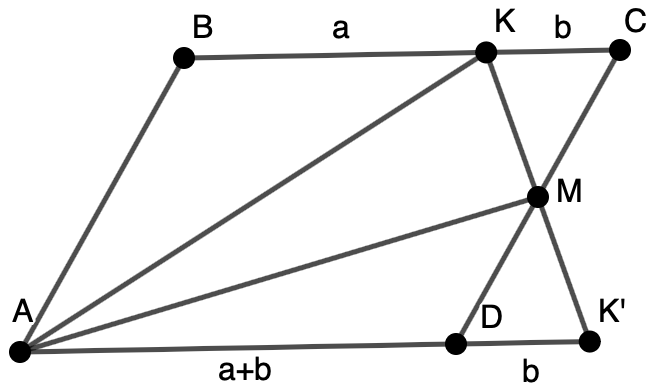
Рассмотрим треугольник . В нем
— высота и медиана одновременно, а значит, по признаку этот треугольник
равнобедренный. Тогда
по определению.
Треугольники и
равны по двум сторонам и углу между ними, так как
по условию,
по
построению,
как вертикальные. Тогда
как соответственные.
как противоположные стороны параллелограмма.
.
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике через точку, делящую ломаную
пополам, провели прямую
параллельную
биссектрисе угла
Аналогично определены прямые
и
Докажите, что
пересекаются в одной
точке.
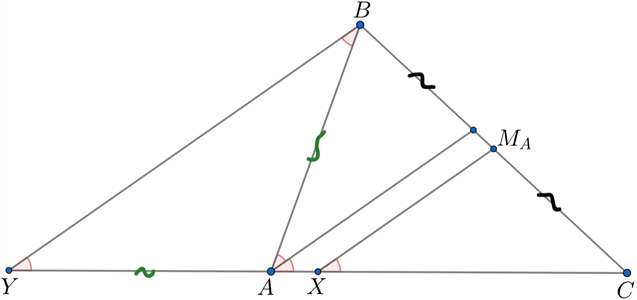
Докажем, что прямая проходит через
— середину стороны
Пусть
Пусть прямые, параллельные биссектрисе угла
проходящие через
и
пересекают прямую
в
и
Тогда
— средняя линия в треугольнике
откуда
а значит
делит ломанную
пополам. Значит доказали, что
проходит через
Следовательно,
— биссектрисы в треугольнике
Ошибка.
Попробуйте повторить позже
На стороне взяли произвольную точку
В треугольники
и
вписаны окружности с центрами
и
соответственно.
Докажите, что окружности
проходят через фиксированную точку, не зависящую от
Докажем, что эта точка является точкой касания вписанной окружности треугольника со стороной
Пусть
— инцентр
треугольника, а описанная окружность
пересекает сторону
в точке
и
в точке
Тогда по лемме о воробьях для
треугольников
и
мы можем сказать следующее про сумму отрезков.
Теперь, вычитая одно из другого получим, что Но это и есть условие для точки касания вписанной окружности
со стороной
Значит,
всё таки точка касания вписанной окружности с
которая не зависит от
и утверждение задачи
доказано.
Ошибка.
Попробуйте повторить позже
В треугольнике провели биссектрису
а в треугольнике
— биссектрису
Прямые
и
пересекаются в точке
Известно, что
Докажите, что
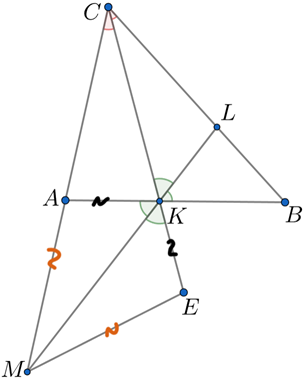
На продолжении за точку
возьмем точку
так, что
т.е.
Т.к.
— биссектриса
и углы
и
вертикальные, то
и соответственно треугольники
и
равны по
-му признаку. Значит,
Получаем
Т.к. по условию то
и значит
откуда
Ошибка.
Попробуйте повторить позже
В треугольнике точка
— середина стороны
, точка
лежит на стороне
. Отрезок
пересекает
в точке
.
Оказалось, что
. Найдите отношение
.
Из условия треугольник
равнобедренный, следовательно,
Проведём среднюю линию где
— середина
треугольника
она будет параллельна
![]()
Следовательно,
а т.к.
то треугольник
равнобедренный.
Тогда
А т.к. — середина
получаем
Ошибка.
Попробуйте повторить позже
В треугольнике провели медиану
Оказалось, что сумма углов
и
равна углу
Найдите отношение
Подсказка 1
В задаче проведена медиана. Тогда какое дополнительное построение можно сразу сделать?
Подсказка 2
Верно, можно удвоить медиану на MD, и получится параллелограмм. Теперь давайте попробуем понять, зачем нам дали равенство про углы. Куда, например, можно перекинуть угол C на картинке, чтобы как-то связать его с углом A?
Подсказка 3
Да, так как получился параллелограмм, то угол C равен накрест лежащему углу. Но тогда что можно сказать про углы ABD и BAD?
Подсказка 4
Верно, они равны из условия, получается та самая сумма углов, и она равна ABM. Значит, ABD равнобедренный треугольник. Найти же нам надо отношение BC и BM. Осталось понять, как связаны BD и AD с ними, и победа!
Удвоим медиану за точку
до точки
тогда
будет параллелограммом, так как точка пересечения диагоналей
делит
их пополам. Значит,
как накрест лежащие.
![]()
Следовательно,
Получаем, что треугольник равнобедренный. Значит,
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике проведена биссектриса
. Диаметр
его описанной окружности перпендикулярен прямой
(порядок точек на описанной окружности
). Окружность, проходящая через точки
и
, пересекает отрезки
и
в точках
и
соответственно. Докажите, что если
, то
.
Подсказка 1
Если сделать аккуратный чертеж, то кажется, что продолжения ХТ, АК и YС пересекаются в одной точке на описанной окружности треугольника АВС.
Подсказка 2
Предыдущий факт сложно доказывать напрямую, стоит применить обратный ход.
Подсказка З
Обозначим пересечение луча АК с описанной окр-тью АВС за L. Пересечение LХ и LY с ВС обозначим Т₁ и Z₁. Хотим показать, что XТ₁Z₁Y является вписанным. Используя, что дуги ВL и LС равны (из-за биссектрисы), можно посчитать сумму противоположных углов данного четырехугольника. Следующий шаг — показать равенство Т₁К и КZ₁.
Подсказка 4
Чтобы показать равенство Т₁К и КZ₁:
Подсказка 5
Осталось показать, что такой четырехугольник единственный. Пересечением чего является центр описанной окружности вписанного четырехугольника? Посмотрите, где лежит центр окружности описанной около XT₁Z₁Y.
Применим обратный ход. Обозначим пересечение луча с
за
Пересечение
и
с
обозначим
и
Теперь
нам надо доказать, что
вписанный и
так как получится, что точки
и
из условия совпадают с
ними.
![]()
Тогда получили, что вписанный, так как внутренний угол равен противоположному внешнему. Теперь обратим внимание на
то, что треугольники
и
подобные, а в прямоугольном треугольнике высота и медиана образуют равны углы со сторонами.
Поэтому так как
высота в треугольнике
то
является медианой в треугольнике
Значит,
середина
откуда получаем то, что мы хотели в начале.
Заметим, что четырехугольник из условия единственный, ведь его центр лежит на серединном перпендикуляре к и на
перпендикуляре к
восставленному в
Ошибка.
Попробуйте повторить позже
В треугольнике
— центр вписанной окружности, вневписанная окружность с центром
касается стороны
в точке
Через
проведена прямая
Оказалось, что
пересекает
в точке
лежащей на средней линии, параллельной
Докажите, что
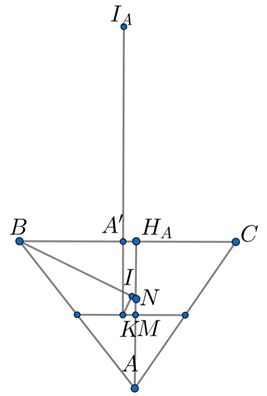
Пусть — высота треугольника,
— ее середина, а
— точка пересечения
с
Тогда точки
— проекции
на
прямые
соответственно — лежат на одной прямой, следовательно, четырехугольник
вписанный и
Так как середина стороны
равноудалена от
и
а
, то
откуда и
следует искомое неравенство.
Ошибка.
Попробуйте повторить позже
На сторонах и
построены вне его квадраты
и
Доказать, что отрезок
в
раза больше медианы
треугольника
Продлим медиану на отрезок равный
Докажем, что треугольник
равен
потому что тогда
Понятно, что
и
Так как
параллелограмм, то
Значит
При этом
Получаем, что треугольники равны по двум сторонам и углу между ними, ч.т.д.
Ошибка.
Попробуйте повторить позже
В трапеции боковая сторона
равна диагонали
. Точка
— середина диагонали
Прямая
пересекает отрезок
в точке
Докажите, что
Достроим треугольник до параллелограмма
Его диагональ
проходит через точку
а, значит, и через точку
Так
как
и прямая
будучи параллельной прямой
не параллельна прямой
— равнобедренная трапеция.
Ее диагонали
и
образуют равные углы с основанием
Следовательно, треугольник
— равнобедренный с основанием
что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
В трапеции Докажите, что
Давайте продлим за точку
на отрезок
равный
Теперь нам нужно доказать, что
так как
У нас получился равнобедренный треугольник
откуда
из параллельности, а
Тогда получаем, что
параллельно
а
параллельно
Значит,
— параллелограмм,
откуда
Ошибка.
Попробуйте повторить позже
На медиане треугольника
нашлась такая точка
что
Кроме того,
Докажите, что
Проведём через точку прямую, параллельную
Отметим на ней точку
так, что
Заметим, что
—
параллелограмм. Значит, достаточно доказать, что
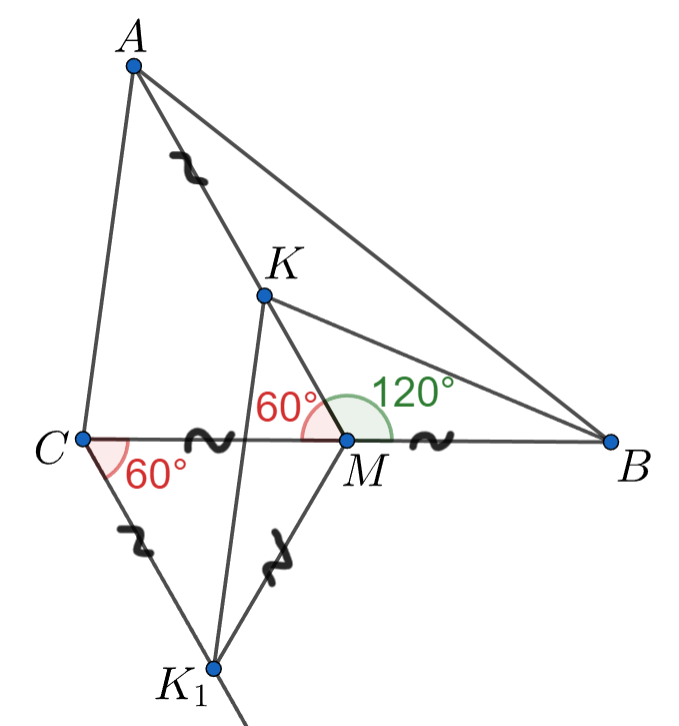
Углы и
равны (по
) как противолежащие. Значит, треугольник
равносторонний. Таким образом,
Также нетрудно видеть, что
Значит, треугольники
и
равны по первому
признаку (
— общая сторона). Отсюда вытекает равенство
и
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике точки
и
— точки пересечения высот и медиан соответственно. Через вершины
и
проведены прямые, перпендикулярные прямым
соответственно. Докажите, что точка пересечения медиан треугольника,
образованного проведёнными прямыми, лежит на прямой
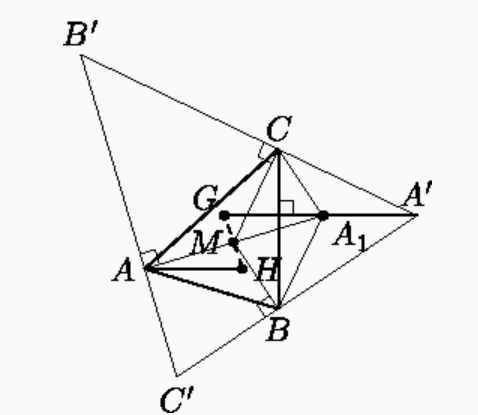
Пусть — треугольник, образованный проведёнными прямыми и
— точка пересечения его медиан. Мы докажем, что
является серединой отрезка
Достроим треугольник до параллелограмма
Отрезок
делит сторону
пополам, поэтому
лежит на
прямой
причём
Кроме того,
и
поэтому
и
— высоты треугольника
Значит,
— ортоцентр этого треугольника и
Стороны треугольника перпендикулярны сторонам треугольника
соответственно, поэтому эти треугольники подобны,
причём соответствующие прямые
и
содержащие медианы этих треугольников, перпендикулярны. Значит, прямая
совпадает с прямой
Пусть
— точка, симметричная точке
относительно
Треугольники
и
симметричны
относительно
поэтому
Отсюда следует, что
лежит на прямой
Аналогично
лежит на прямой
то
есть
совпадает с



