Ошибка.
Попробуйте повторить позже
Два треугольника пересекаются по шестиугольнику , в котором
Найдите углы этих треугольников.
Источники:
Подсказка 1
Обратите внимание, что есть два случая для пересечения треугольников.
Случай (стороны треугольника - тройки несмежных сторон):
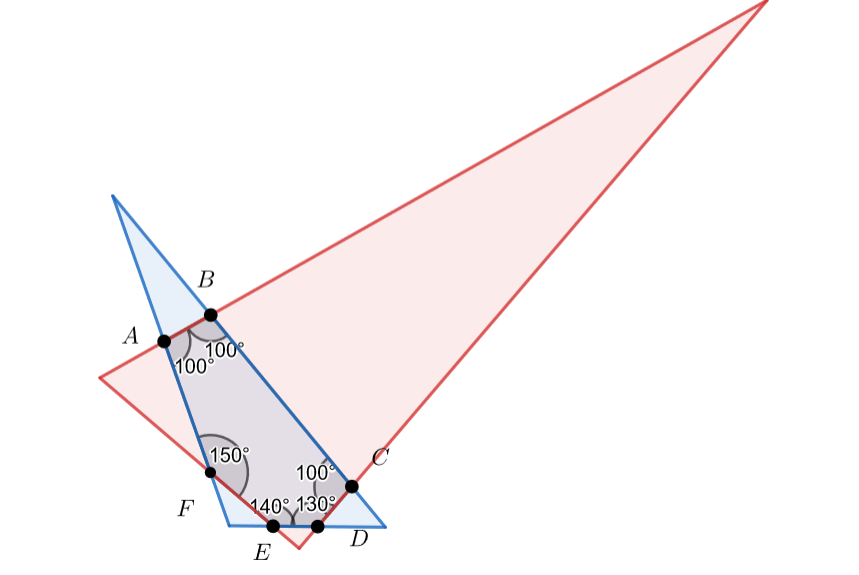
В таком случае все углы треугольников легко находятся, как , где
- два соседних угла
шестиугольника.
Тогда получаем, что углы красного треугольника равны , а углы синего -
.
Случай (один из углов шестиугольника совпадает с углом треугольника):
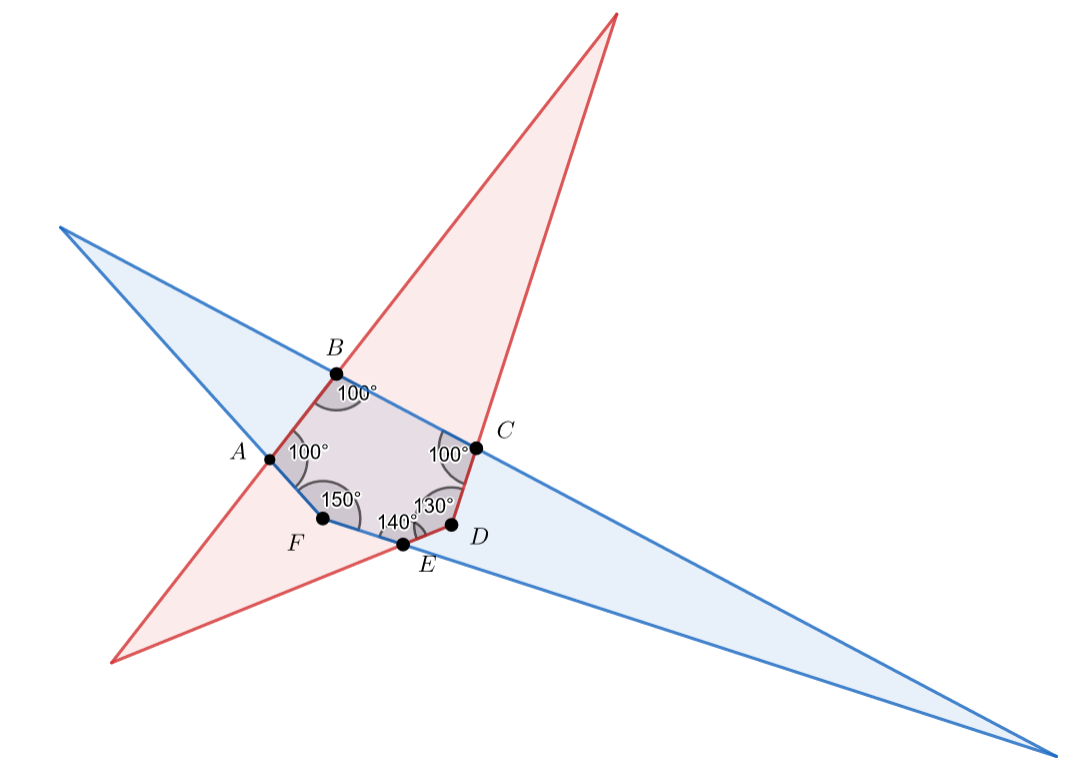
Заметим, что это единственное возможное положение в этом случае. Углы синего треугольника равны ;
и
.
Углы красного треугольника будут равны
и
.
и
; или
и
Ошибка.
Попробуйте повторить позже
Неравнобедренный треугольник в котором
вписан в окружность
На биссектрисе угла
выбрана точка
а на биссектрисе угла
— точка
так, что
и
Прямая
пересекает
в точках
и
Докажите,
что треугольник
равнобедренный.
Так как то
Аналогично
Обозначим
Пусть
Обозначим
через
середину дуги
окружности
Тогда треугольник
равносторонний(
). Поэтому точка
—
центр описанной окружности треугольника
Следовательно:
Аналогично откуда
Итак, точка лежит на прямой
будем считать, что она совпадает с
Пусть
— середина меньшей дуги
окружности
Заметим, что
Значит, точка также лежит на прямой
и треугольник
совпадает с треугольником
Этот треугольник
равнобедренный, поскольку
![]()
Ошибка.
Попробуйте повторить позже
Равносторонние треугольники и
расположены так, что вершина
лежит на стороне
, а вершина
— на стороне
.
Докажите, что
.
Подсказка 1
Хм, здесь есть много равных углов. Это намекает на то, что стоит поискать вписанные четырёхугольники!
Подсказка 2
Конечно, тут есть два вписанных четырёхугольника, имеющих общую сторону CR. Как же воспользоваться их вписанностью?
Подсказка 3
Верно, используем факт, что противоположные углы в сумме дают 180 градусов, надо просто перекинуть уголки, чтобы получить нужную сумму односторонних углов для искомых прямых!
Проведем рассмотрим четырехугольники
и
.
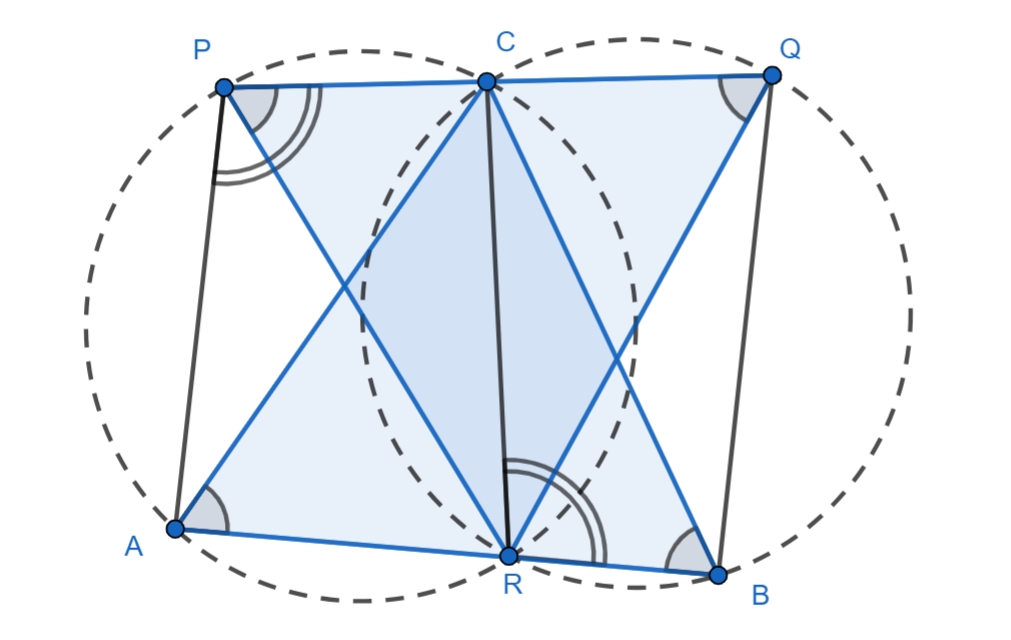
Поэтому
Следовательно,
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
В треугольнике проведены высоты
и
, а
. Докажите, что
— диаметр окружности девяти точек
треугольника
Подсказка 1
Угол в 45 градусов…Где же он встречается…Ого, а что насчет треугольников BA1A и BC1C? Что про них можно сказать? А что это дает?
Подсказка 2
Верно, они прямоугольные и равнобедренные, но тогда высоты в этих треугольниках - это серединные перпендикуляры. А значит пресечения высот в этих треугольниках - центр описанной окружности треугольника ABC. Нам нужно доказать, что в четырехугольнике C1OA1H точкой пересечения диагоналей, диагональ OH делится пополам. А где еще мы что-то очень похожее слышали? Что можно сказать про этот четырехугольник?
Подсказка 3
Поскольку данный четырехугольник образован серединными перпендикулярами и высотами в одном треугольнике, то данный четырехугольник является параллелограммом. А что мы знаем насчет диагоналей параллелограмма?
Подсказка 4
Верно, OH делится A1C1 пополам. Стоп, то есть середина отрезка OH является еще и серединой отрезка A1C1? Но ведь середина ОН - это всегда центр окружности Эйлера! А не решили ли мы задачу?
По условию , а значит
и
— равнобедренные. Отсюда
лежит на серединном перпендикуляре к
, а
— на серединном перпендикуляре к
. Также на обоих перпендикулярах находится точка
. Но тогда
, откуда
. Аналогично
, откуда
— параллелограмм, а значит
делится
пополам.
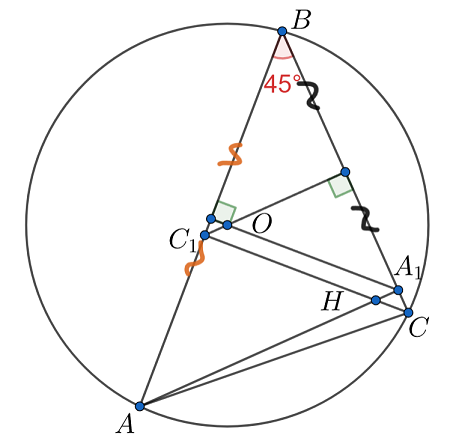
Сделаем гомотетию в ортоцентре с коэффициентом . Нетрудно понять, что описанная окружность перейдёт в окружность Эйлера.
Также очевидно, что
перейдёт в середину отрезка
, значит она и является центром окружности Эйлера. Таким образом, получили
требуемое.
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
и
— высоты остроугольного треугольника
, в котором
. Точки
и
— соответственно центр
описанной окружности и ортоцентр треугольника
. Докажите, что прямая
проходит через середину отрезка
.
Подсказка 1
Угол в 45 градусов…Где же он встречается…Ого, а что насчет треугольников BA1A и BC1C? Что про них можно сказать? А что это дает?
Подсказка 2
Верно, они прямоугольные и равнобедренные, но тогда высоты в этих треугольниках - это серединные перпендикуляры. А значит пресечения высот в этих треугольниках - центр описанной окружности треугольника ABC. Нам нужно доказать, что в четырехугольнике C1OA1H точкой пересечения диагоналей, диагональ OH делится пополам. А где еще мы что-то очень похожее слышали? Что можно сказать про этот четырехугольник?
Подсказка 3
Поскольку данный четырехугольник образован серединными перпендикулярами и высотами в одном треугольнике, то данный четырехугольник является параллелограммом. А что мы знаем насчет диагоналей параллелограмма?
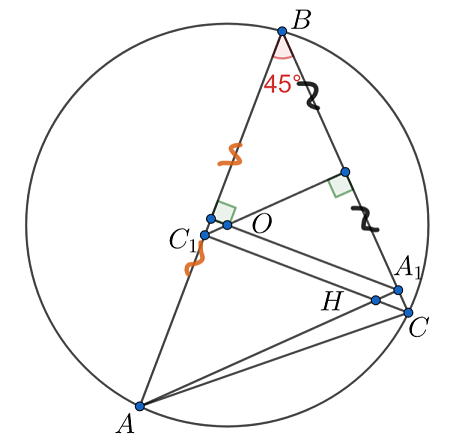
По условию , а значит,
и
— равнобедренные. Отсюда
лежит на серединном перпендикуляре к
,
а
— на серединном перпендикуляре к
. Также на обоих перпендикулярах находится точка
. Но тогда
, откуда
. Аналогично
, откуда
— параллелограмм, а значит
делится
пополам, что и
требовалось.
что и требовалось доказать
Ошибка.
Попробуйте повторить позже
В прямоугольном треугольнике точка
— середина гипотенузы
На катетах
и
отмечены точки
и
соответственно так, что
Докажите, что
.png)
Чтобы доказать это равенство, соберём все отрезки в один прямоугольный треугольник и применим теорему Пифагора.
Удвоим до точки
за точку
Заметим, что
является параллелограммом, поскольку его диагонали пересекаются в
своих серединах. Отсюда
и
Остаётся доказать, что (и из треугольника
мы получим требуемое). Но действительно,
является медианой (по
построению) и высотой (по условию) треугольника
откуда он равнобедренный и
Ошибка.
Попробуйте повторить позже
В треугольнике медиана, проведённая из вершины
в четыре раза меньше стороны
и образует с этой стороной угол
Найдите угол
Обозначим медиану из вершины через
Первое решение.
Опустим перпендикуляр на прямую
Тогда в прямоугольном треугольнике
катет
равен половине гипотенузы
так как лежит напротив угла в
градусов. А ещё по условию
Тогда
Получили, что в четырёхугольнике
диагонали точкой пересечения
делятся пополам, а значит, это параллелограмм, так что
В итоге
Второе решение.
Отметим ещё середину — как
а середину
— как
Тогда
а ещё по условию
Так что
треугольник
— равносторонний (
) с углом при вершине
в
значит, он равносторонний.
Тогда как смежный с углом в
Далее,
поэтому треугольник
— прямоугольный, и
Смежный с ним
С другой стороны, этот же угол равен
так как
— средняя линия
треугольника
— параллельна
Третье решение.
Не будем думать и просто посчитаем:
1) по теореме косинусов для треугольника
2) по формуле медианы (при удвоение медианы получается параллелограмм, у которого сумма квадратов диагоналей равна сумме квадратов всех сторон)
3) по теореме косинусов для треугольника
Ошибка.
Попробуйте повторить позже
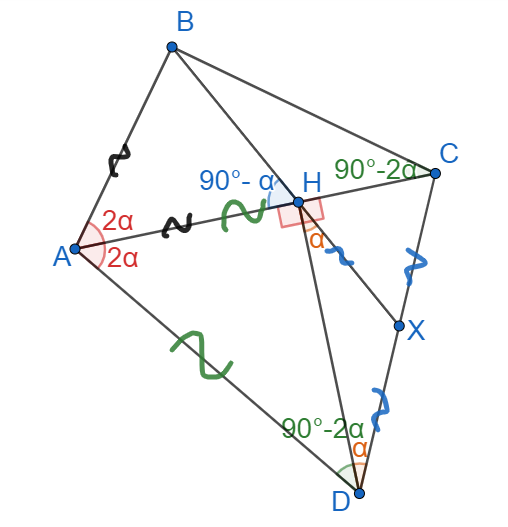
В выпуклом четырёхугольнике угол
— прямой, а диагональ
является биссектрисой угла
и равна стороне
В
треугольнике
провели высоту
Докажите, что прямая
делит отрезок
пополам.
Пересечём и
в точке
Пусть
Заметим, что
по гипотенузе и прилежащему углу,
откуда
а значит
Следовательно,
Также в силу вышеупомянутого равенства треугольников
— равнобедренный, откуда
Теперь видно, что
то есть — равнобедренный, а значит
Далее совсем нетрудно убедиться, подсчитав углы в
что
также равнобедренный, следовательно
что и требовалось.
Ошибка.
Попробуйте повторить позже
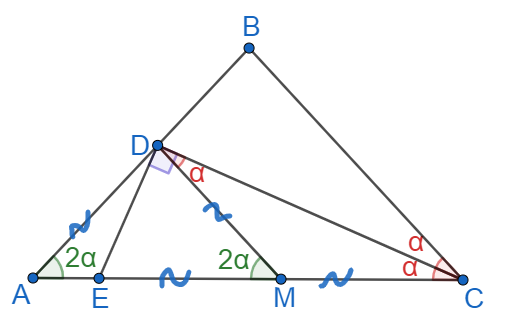
В равнобедренном треугольнике с основанием
проведена биссектриса
Прямая, проходящая через точку
перпендикулярно
пересекает
в точке
Докажите, что
Пусть — середина отрезка
тогда
поскольку
— прямоугольный. Заметим, что достаточно доказать, что
— равнобедренный. Пусть
тогда
Также
как внешний угол у равнобедренного
получили требуемое.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены медианы
и высоты
Докажите, что длина ломаной
равна периметру треугольника
Заметим, что каждое из звеньев этой ломаной является медианой в прямоугольном треугольнике, проведённой к гипотенузе, а значит:
тогда если просуммировать длины этих отрезков, получится величина что и требовалось.
Ошибка.
Попробуйте повторить позже
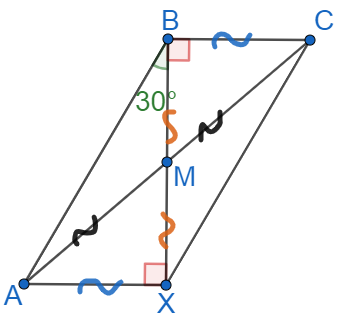
Найдите отношение двух сторон треугольника, если его медиана, выходящая из той же вершины, образует с этими сторонами углы и
Удвоим медиану и заметим, что — прямоугольный с углом
а значит катет напротив этого угла равен половине гипотенузы, то
есть
а значит искомое отношение равно
Ошибка.
Попробуйте повторить позже
В четырехугольнике два противоположных угла прямые, а соединяющая их диагональ делится пополам другой диагональю. Докажите, что эти диагонали либо равны, либо перпендикулярны.
Пусть углы и
данного четырехугольника
прямые, а его диагонали пересекаются в точке
1 случай.
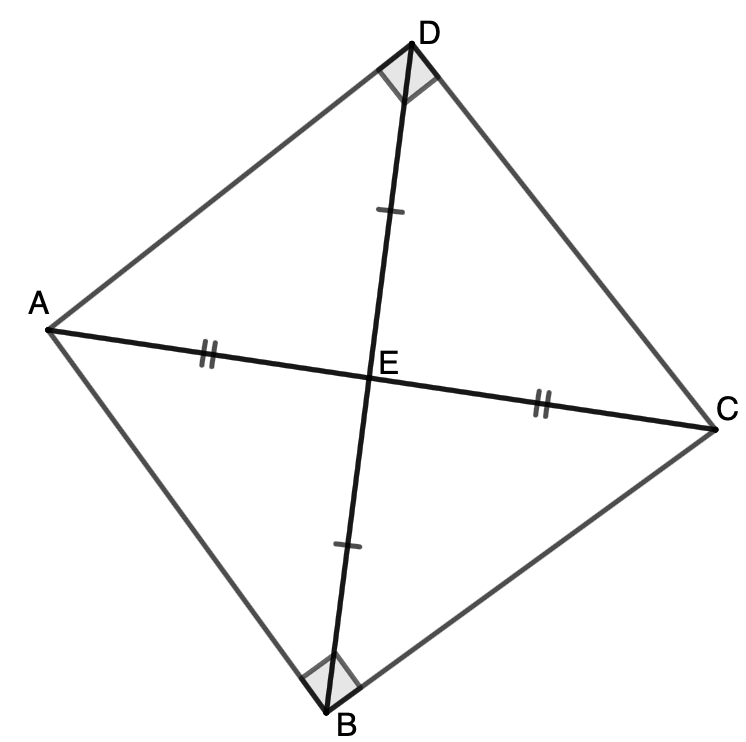
Рассмотрим треугольник Он прямоугольный, и в нем
— медиана. Значит,
Аналогично
Следовательно,
2 случай.
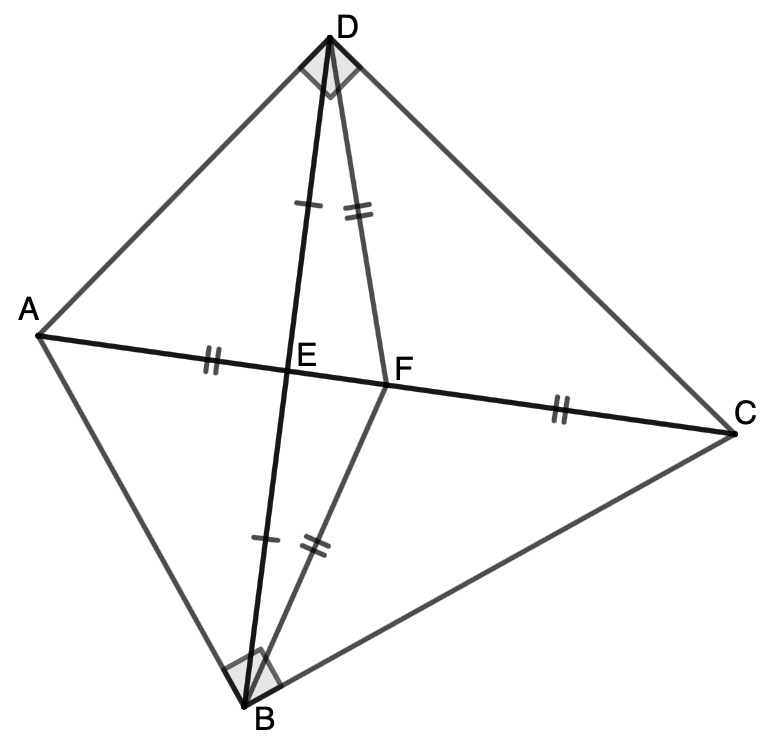
Пусть — середина
Тогда в прямоугольном треугольнике
— медиана. Значит,
Аналогично
Значит,
то есть треугольник
равнобедренный. Тогда
— медиана этого равнобедренного треугольника, а значит,
и высота. Следовательно,
содержащий отрезок
перпендикулярен
Ошибка.
Попробуйте повторить позже
В остроугольном неравнобедренном треугольнике проведены высоты
и
и отмечены точки
и
— середины
сторон
и
соответственно. Докажите, что если
то
Источники:
Подсказка 1
Давайте для начала подумаем, что нам дает равенство уголочков ∠ABC и ∠A₁MC₁. Мы знаем, что сумма уголков ∠C₁MA+∠C₁MA₁+∠A₁MC=180°. Как нам выразить ∠C₁MA и ∠A₁MC через углы треугольника ∠ABC?
Подсказка 2
Т.к. △AMC₁ и △CMA₁- равнобедренные, то ∠AMC₁=180°-2∠BAC, ∠CMA₁=180°-2∠BCA ⇒ ∠ABC=2(180°-∠ABC)-180° ⇒ ∠ABC=60°. Тогда очень интересным выглядит треугольник △BC₁C. Что можно сказать про сторону BC₁?
Подсказка 3
Верно, она равна BC/2. Но мы знаем, что BL=BC/2 ⇒ BC₁=BL. Из аналогичных рассуждений можно получить, что BK=BA₁. Как тогда завершить решение?
Подсказка 4
Посмотрите на равенство BC₁-BK=BL-BA₁!
![]()
Давайте сначала узнаем, для чего же нам дали равенство углов. Пусть Тогда можем выразить угол
через два других угла треугольника. Понятно, что
Тогда
Но мы знаем, что Тогда
Отлично! Значит, на самом деле нам дали треугольник с углом Но тогда
так как
— это средняя линия
треугольника, а
подобен исходному с коэффициентом
откуда и получаем равенство. Теперь видим, что если докажем
равенство треугольников
и
то мы победим! Одна пара сторон у них равные, а
общая сторона. Давайте найдём угол
между ними. Будем использовать знания о том, что
вписанный,
параллельно
и из прямоугольного треугольника
Тогда
Значит, треугольники и
равны по двум сторонам и углу между ними. Тогда и
Победа!
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике с углом
при вершине
проведены высоты
и
Луч
пересекает прямую
в точке
Оказалось, что
Найдите углы треугольника
Источники:
Подсказка 1
Даны параллельность и вписанность - это сразу же намекает нам на углы! Попробуем поотмечать, а потом воспользуемся условием на угол A) Что узнаем?
Подсказка 2
Понимаем, что AF = FC! Теперь мы можем посчитать достаточно большое количество углов на картинке...но все из них равны либо 90, либо 90/2. На что это может намекать? Обратим внимание на точку F.
Подсказка 3
Угол AFC в 2 раза больше чем AXC. Чем тогда является F для треугольника AXC? Когда мы это поймем, мы сможем по аналогии связать углы AFX=EFB и ACB. Не забываем про вписанность!)
![]()
Из условия следует, что . Из вписанностей
, и теперь из параллельности
. В треугольнике
точка
оказалась центром описанной окружности (равноудалена от вершин
и
и центральный угол в два раза больше вписанного).
Поэтому
, что вместе со вписанностью
дает
Ошибка.
Попробуйте повторить позже
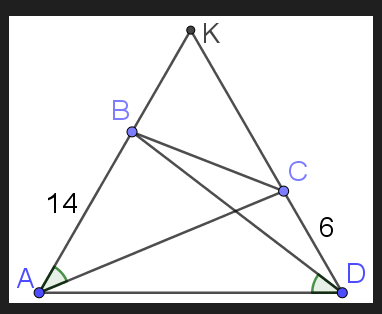
Выпуклый четырёхугольник таков, что
и
. Найдите длину
, если известно, что
Подсказка 1
Два прилежащих угла четырёхугольника равны по 60 градусов. Какое удобное дополнительное построение можно сделать, чтобы получить эти углы уже в треугольнике?
Подсказка 2
Конечно, продлить AB и CD до пересечения в точке K и получить равносторонний треугольник. Поэтому можно искать не AD, а, например, KA или KD, так как они равны. Как теперь воспользоваться равенством углов ∠ BAC и ∠ BDA?
Подсказка 3
Докажите равенство треугольников △KCA и △BAD
Продлим стороны и
до пересечения в точке
. Заметим, что
, а значит, треугольник — равносторонний.
Тогда треугольники
и
равны по двум углам:
,
по условию; и прилежащей
стороне:
. Тогда
и сторона равностороннего треугольника равна
, а значит, и
Ошибка.
Попробуйте повторить позже
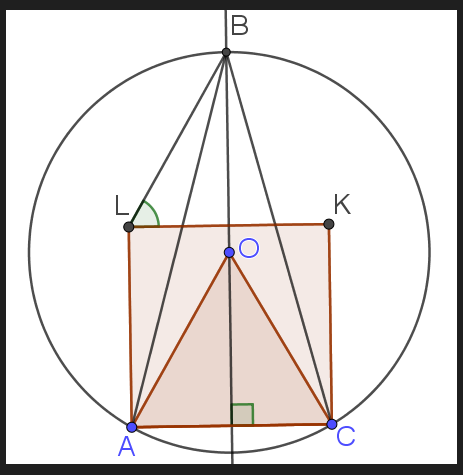
В равнобедренном треугольнике (
) радиус описанной окружности равен стороне
. На стороне
построили квадрат
так, что
пересекает боковые стороны треугольника. Найдите угол
Подсказка 1
Трудно работать с окружностью, когда мы не знаем, где ее центр. Тем более, удобно отметить его, если треугольник, который вписан в эту окружность - равнобедренный. Давайте отметим центр описанной окружности O и поймем что-то про эту точку и отрезки, которые она соединяет.
Подсказка 2
Верно, BO = OA, при этом OA = AC, и при этом AC = CL. Значит, BO = LA. Что тогда можно сказать про четырехугольник ALBO? Мы ведь еще никак не связали с картинкой BO(ну почти никак).
Подсказка 3
Можно сказать, что BO перпендикулярно AC, а значит, параллельно AL. Тогда, выходит, что ALBO - параллелограмм. Но ведь тогда AO || LB. Что тогда можно сказать, зная это и что AOC - равносторонний?
Обозначим центр описанной окружности треугольника за . Тогда
, а также
. Так как
треугольник
равнобедренный, то
— является высотой, а значит,
. А также
. Таким образом,
и
, а значит,
— параллелограмм, откуда
.
Аналогично получаем, что , а значит,
и треугольник
— равносторонний, а значит,
.
Ошибка.
Попробуйте повторить позже
Найдите величину угла, изображенного на картинке ниже.
![]()
Подсказка 1
Смотря на картинку, сразу хочется достроить чертеж до треугольника) Каким он получится?
Проведём третий отрезок и получим равнобедеренный треугольник (см. рисунок ниже). Заметим, что треугольники
и
равны по двум сторонам и прямому углу
, равному
, а значит,
. Тогда
. Откуда получаем, что , а значит, из равнобедренности,
![]()
Ошибка.
Попробуйте повторить позже
В окружность вписан четырёхугольник , диагонали которого взаимно перпендикулярны и пересекаются в точке
. Прямая,
проходящая через точку
и перпендикулярная к
, пересекает сторону
в точке
.
а) Докажите, что — медиана треугольника
;
б) Найдите , если
.
Подсказка 1!
1) У нас в задаче есть прямоугольные треугольники(много), а еще вписаности! На что это намекает обычно, какие мы можем извлечь из этого полезные факты?
Подсказка 2!
2) Да, на такой картинке удобно считать углы! Давайте этим и воспользуемся для доказательства пункта а, и попробуем доказать, что EM - медиана DEA (который, кстати, является прямоугольным треугольником, что-то мы знаем про его медиану..!)
Подсказка 3!
3) Итак, в пункте б нам нужно найти медиану прямоугольного треугольника, то есть половину его гипотенузы! Мы знаем его угол, а значит, нам достаточно посчитать любой из катетов!
Подсказка 4!
4) Осталось аккуратно, пользуясь удачно большим количеством прямоугольных треугольников, посчитать EM
![]()
а) Поскольку , то
. Поскольку
(
) является высотой в прямоугольном
треугольнике
, то
, как вертикальные, откуда
будет медианой в прямоугольном
треугольнике.
Замечание. Указанный в задаче факт известен как "теорема Брахмагупты". Но так как в пункте (а) задача явно заключается в том, чтобы доказать напрямую это утверждение, не следует просто так ссылаться на эту теорему!
Можно также заметить, что прямые и
антипараллельны относительно угла
, а высота
прямоугольного
треугольника
, как известно, является также симедианой в этом треугольнике, соответственно делит антипараллельный отрезку
отрезок
пополам.
б) Заметим, что
В силу перпендикулярности диагоналей четырёхугольника отрезок можем, во-первых, найти по теореме Пифагора из треугольника
А во-вторых, из треугольника
Ошибка.
Попробуйте повторить позже
Докажите, что высота прямоугольного треугольника делит гипотенузу в отношении квадратов катетов.
Подсказка 1
Заметьте, что из-за прямых и общих углов получилось получилось 3 подобных треугольника. Тогда что можно сделать?
Подсказка 2
Записать отношение сторон! Остаётся их аккуратно скомбинировать, чтобы выделить нужные отрезки
Подсказка 3
Хм. а какой вообще луч делит сторону в отношении квадратов прилежащих сторон? Симедиана! Так можно просто попробовать доказать, что высота в прямоугольном треугольнике является симедианой
![]()
Пусть и
— высота и медиана треугольника
где
Первое решение. Заметим, что Отсюда
Второе решение. Заметим, что и, тогда по свойству симедианы
имеем
Ошибка.
Попробуйте повторить позже
На диагонали выпуклого четырехугольника
отмечена точка
. Известно, что
u
. Докажите, что
.
![]()
Отметим на отрезке точки
и
так, что
, чтобы получить
и
. Причём как внешние
углы
и
. Следовательно, треугольник
правильный, а тогда
. Так как
, то получаем, что точка
совпадает с
, поэтому
. Кроме того,
, как гипотенуза и меньший катет
прямоугольного треугольника с углом
. Итак,
по неравенству треугольника, что и
требовалось.



