Ошибка.
Попробуйте повторить позже
Точки лежат в вершинах клеток клетчатой бумаги. Может ли угол
оказаться равным
Источники:
Подсказка 1
Угол может располагаться вообще как угодно, неприятно. Давайте использовать линии сетки. Проведём из точки В луч горизонтальный и опустим на него перпендикуляры АЕ и СF, получим углы α = АВЕ и β = CBF (возможно, какой-то из них нулевой! если Е или F на одной линии с В). Что мы можем найти для этих углов?
Подсказка 2
Можем найти тангенс α и β. Теперь давайте вычислим тангенс АВС с помощью формулы тангенса суммы. Поразмышляйте над полученным выражением: что же нам даёт расположение точек в узлах сетки... давайте, не ленитесь, не хочу лишать Вас удовольствия
Подсказка 3
Оп-па, а это выражение (тангенс суммы) рационален! А тангенс 30 градусов нет. Развалили задачу
Проведем из точки луч по линии сетки:
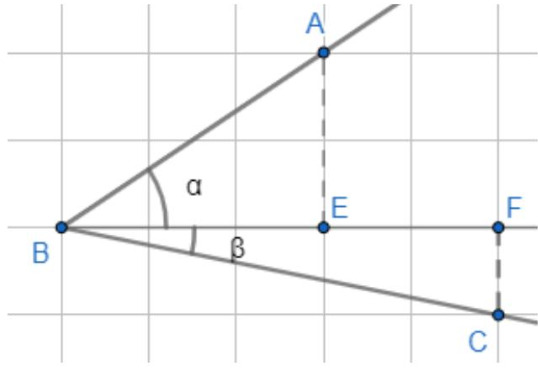
Тогда угол будет равен сумме углов
и
(они могут быть и отрицательными). Тангенс такого угла равен отношению двух
целых чисел, то есть является рациональным числом. Тогда
также рациональное число. Но — число иррациональное.
Если один из углов и
является прямым, то можно использовать луч, идущий перпендикулярно первому.
Ошибка.
Попробуйте повторить позже
и
— биссектрисы треугольника
Оказалось, что
— биссектриса угла
Найдите угол
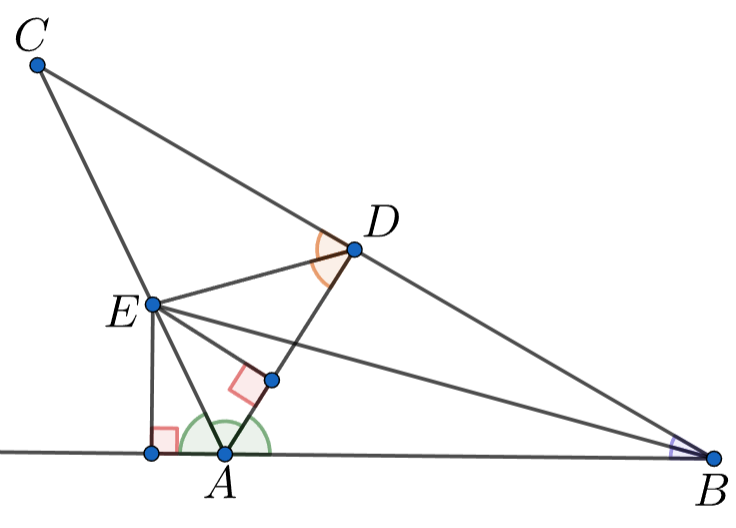
Из условия следует, что точка равноудалена от прямых
и
Значит,
— биссектриса угла
так как
равноудалена от
и
Таким образом,
а в сумме эти три угла дают
значит каждый из них равен
по
а угол
—
Ошибка.
Попробуйте повторить позже
На плоскости расположен правильный треугольник со стороной 3. Сколько существует точек
на плоскости таких, что выполнены
равенства
, и
?
Рассмотрим произвольную точку такую, что
. Опустим перпендикуляр из
на
. Пусть
— основание этого
перпендикуляра. Тогда
, откуда
. То есть данное
условие для
выполнено тогда и только тогда, когда оно выполнено для
. Заметим, что
не может лежать на
продолжении стороны
за точку
. Также
не может лежать на продолжении стороны
за точку
, так как
иначе
. На отрезке
такая точка найдется, причем она будет единственной.
Таким образом, ГМТ точек
таких, что
будет прямой, перпендикулярной
, проходящей через
. Аналогичные рассуждения можно провести и с точками
такими, что
. То есть точка
должна
одновременно лежать на пересечении двух полученных прямых, причем прямые между собой образуют угол
, поэтому они
пересекутся.
Ошибка.
Попробуйте повторить позже
Дан прямоугольник Найдите ГМТ
, для которых
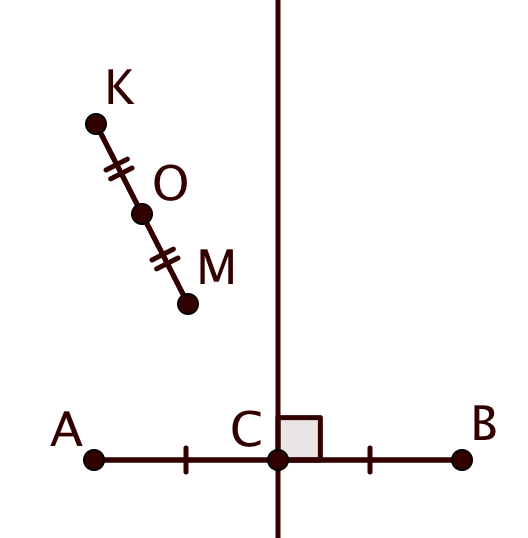
Проведем серединный перпендикуляр к отрезку Так как
— прямоугольник, он также будет являться серединным
перпендикуляром к отрезку
Обозначим этот серединный перпендикуляр через
и покажем, что он и является искомым
ГМТ.
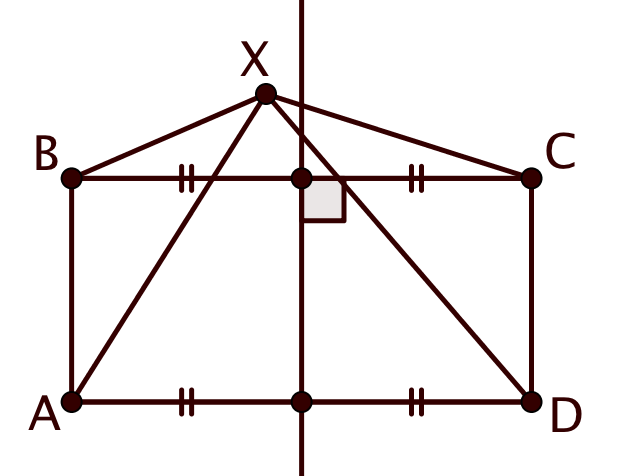
Во-первых, очевидно, что любая точка с подходит: в самом деле, так как
— серединный перпендикуляр, то для всех точек
верно
поэтому
Во-вторых, покажем, что никакая другая точка не подходит. Рассмотрим произвольную точку не на
скажем,
не умаляя общности, что точка
находит по одну сторону относительно
что и точки
и
Тогда выполнено
Поэтому
и необходимое равенство не выполнено. Аналогично для
лежащей по одну
сторону с
и
относительно
выполнено
Таким образом, никакие точки, отличные от
точек
не подходят, значит, искомое ГМТ — прямая
являющаяся серединным перпендикуляром к отрезкам
и
Ошибка.
Попробуйте повторить позже
(a) Как известно, серединный перпендикуляр — ГМТ, равноудаленных от концов отрезка. Обозначим середину отрезка через
.
Тогда совершенно очевидно, что для точек
на луче
расстояние до точки
меньше, чем до
, а для точек на луче
—
наоборот, расстояние до точки
больше, чем до
.
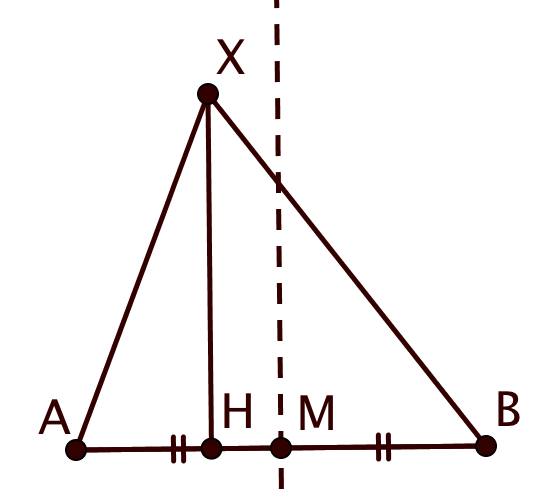
Теперь рассмотрим произвольную точку плоскости. Обозначим её проекцию на прямую
через
. Если точка
лежит по
одну сторону с точкой
относительно серединного перпендикуляра, то и
лежит на луче
. Тогда
, а по
теореме Пифагора
, или
, то есть для любой точки, лежащей по
одну сторону от серединного перпендикуляра с точкой
, расстояние до
меньше, чем до
. Аналогично для точки,
лежащей по одну сторону с
относительно серединного перпендикуляра расстояние до
меньше, чем до
. Отсюда и
ответ.
(b) Обозначим середины сторон ,
и
через
,
и
соответственно, а точку пересечения серединных
перпендикуляров к сторонам треугольника
через
. Тогда искомое ГМТ — угол, образованный как пересечение двух
полуплоскостей, ограниченных прямыми
и
. Полуплоскость, ограниченная прямой
, включает точку
, а полуплоскость,
ограниченная прямой
, включает точку
.
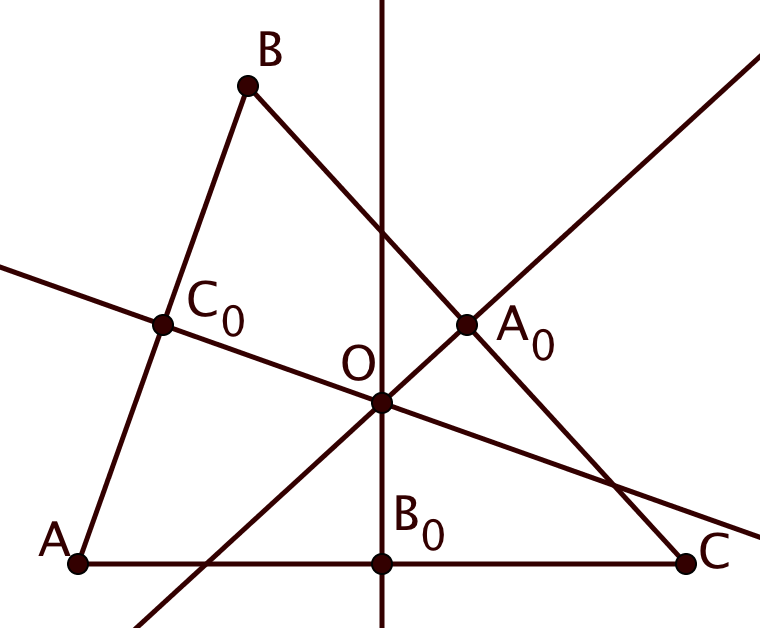
Как мы знаем по пункту (а), ГМТ , для которых
, — полуплоскость, ограниченная прямой
, содержащая точку
.
Также, ГМТ
, для которых
, — полуплоскость, ограниченная прямой
, содержащая точку
. Поэтому все точки
,
подходящие под условие
, могут лежать только в пересечении этих двух полуплоскостей. Более того, если точка лежит в
этом пересечении, то по тому же пункту (а), она удовлетворяет двум неравенствам
и
, поэтому двойное неравенство
также верно.
(c) Обозначим середину через
и проведем к
серединный перпендикуляр. Так как
, то по пункту (а) точка
лежит по ту же сторону относительно этого серединного перпендикуляра, что и
. Аналогично, точка
также лежит относительно
серединного перпендикуляра по ту же сторону, что и
.
Тогда, так как обе точки и
лежат по одну сторону относительно серединного перпендикуляра, то и середина отрезка
,
точка
, также лежит по одну сторону с точкой
относительно серединного перпендикуляра к
. Значит, по тому же пункту (а),
расстояние от
до
меньше, чем до
, или
Ошибка.
Попробуйте повторить позже
Все углы пятиугольника равны. Докажите, что серединные перпендикуляры к сторонам
и
пересекаются на
биссектрисе угла
Обозначим точку пересечения серединных перпендикуляров к и
через
. Продлим отрезки
и
за точки
и
до
пересечения в
, аналогично продлим отрезки
и
за
и
до пересечения в точке
. Так как углы исходного пятиугольника
равны, то и смежные с ними углы также равны:
,
. Поэтому треугольники
и
—
равнобедренные,
и
. Значит, точки
и
лежат на серединных перпендикулярах к отрезкам
и
, и эти
же серединные перпендикуляры в треугольниках
и
являются биссектрисами углов
и
. Поэтому в треугольнике
прямые
и
являются биссектрисами. Поэтому третья биссектриса треугольника, то есть биссектриса
, проходит
через точку
Ошибка.
Попробуйте повторить позже
В треугольнике проведены биссектриса
и высота
. Оказалось, что серединный перпендикуляр к отрезку
пересекает
сторону
в её середине. Докажите, что треугольник
— равнобедренный.
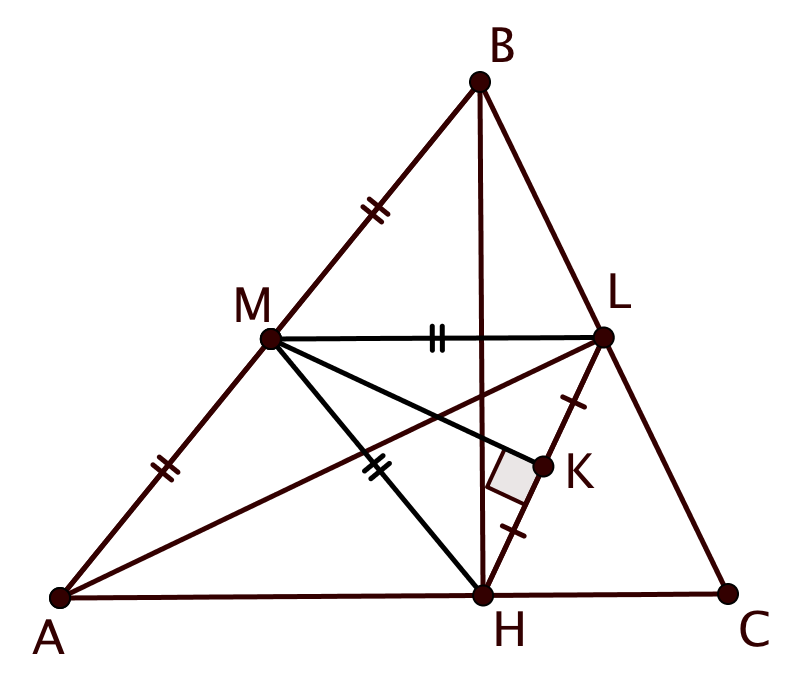
Обозначим середину через
. По условию
лежит на серединном перпендикуляре к
, значит,
. При этом так как
— высота,
— медиана прямоугольного треугольника
. Поэтому также медиана равна половине гипотенузы:
. Отсюда же
, и в треугольнике
медиана
равна половине стороны, к которой она
проведена. Поэтому
. Значит, в треугольнике
биссектриса
также является и высотой, поэтому треугольник
— равнобедренный,
, что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
Дан треугольник Внутри него взяли точку
и соединили ее с вершинами. Получилось три треугольника. Найдите ГМТ
для
которых сумма площадей двух из этих треугольников будет равна площади третьего.
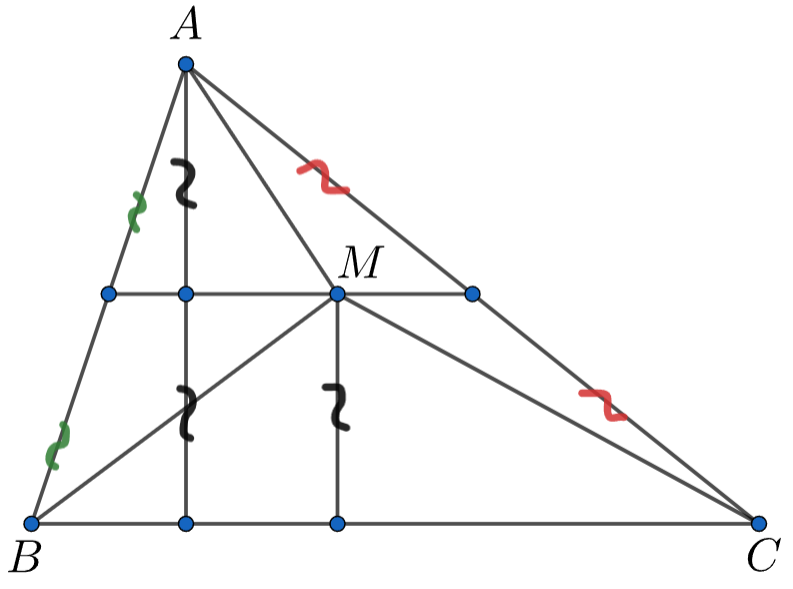
Пусть Но тогда
то есть
У треугольников
и
одинаковое основание
Значит, высота, проведённая к
у треугольника
в
раза меньше соответствующей высоты у
треугольника
Следовательно, все такие точки
находятся на расстоянии половины высоты треугольника
проведённой к
от прямой
Осталось заметить, что все такие точки находятся на средней линии, потому что она делит высоту треугольника
пополам и параллельна
серединный треугольник , то есть треугольник, образованный тремя средними линями
Ошибка.
Попробуйте повторить позже
Найдите ГМТ середин хорд длины в данной окружности.
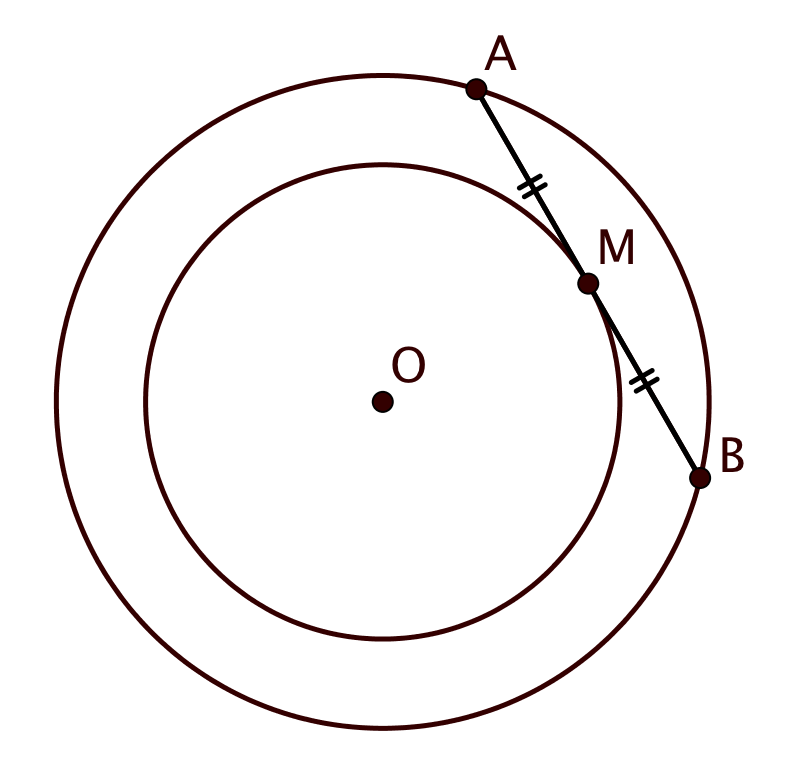
Рассмотрим произвольную точку , удовлетворяющую условию, и обозначим отрезок длины
, серединой которого она является, через
. Тогда
как медиана равнобедренного
. Поэтому по теореме Пифагора
, значит, точка
лежит на указанной окружности.
В другую сторону, рассмотрим произвольную точку , лежащую на окружности из ответа. Проведем к этой окружности касательную,
обозначим точки пересечения этой касательной с исходной окружностью через
и
. Тогда
как радиус, проведенный
в точку касания. Поэтому
и
можно найти из теоремы Пифагора для прямоугольных
и
:
, откуда
. Значит,
, и указанная точка
является серединой хорды
длины
.
Обозначим центр исходной окружности через и радиус через
. Тогда искомое ГМТ — окружность с центром
и радиусом
Ошибка.
Попробуйте повторить позже
Докажите, что у любого треугольника есть три вневписанных окружности.
Во-первых, отметим, что точка пересечения двух внешних биссектрис углов
и
подходит в качестве центра
вневписанной окружности: эта точка, так как лежит на биссектрисе внешнего
, равноудалена от прямых
и
, по
аналогичным соображениям она равноудалена от прямых
и
, значит, равноудалена от всех трех прямых, содержащих стороны
треугольника
. Поэтому окружность с центром в этой точке, касающейся одной из прямых, будет касаться и всех остальных. Итого
три вневписанные окружности мы нашли.
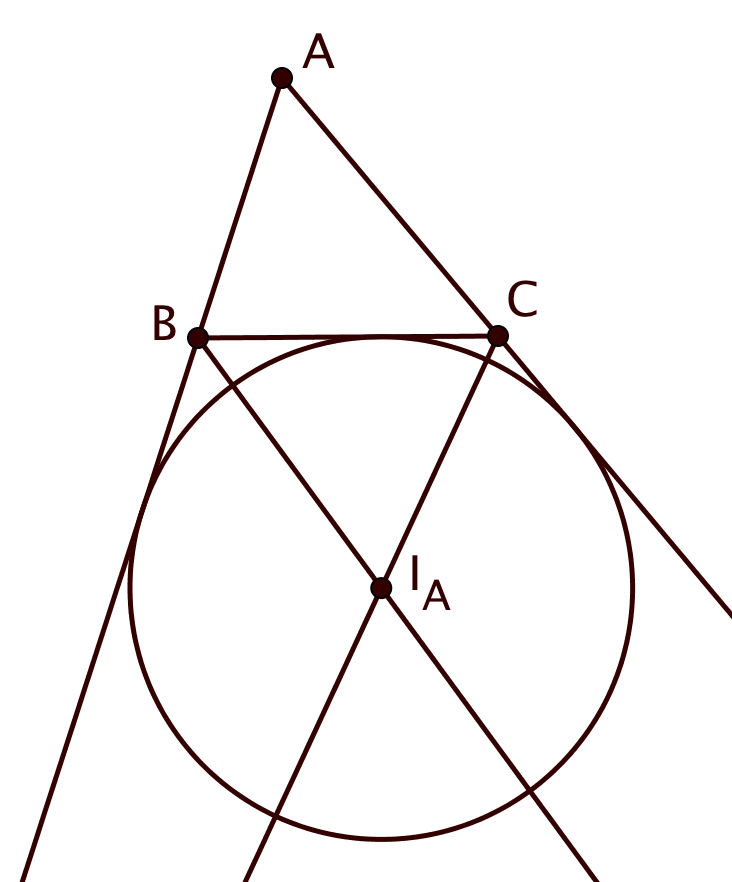
Предположим, что существуют еще какие-то вневписанные окружности. Рассмотрим центр одной из них. Тогда он равноудален от всех трех прямых, содержащих стороны, а значит лежит либо на внутренних биссектрисах, либо на внешних. Но все точки их пересечения мы уже рассмотрели и соответствующие вневписанные окружности нашли, значит, другие вневписанных окружностей нет.
Ошибка.
Попробуйте повторить позже
В четырёхугольнике
.
— середина
,
— середина
. Серединные перпендикуляры к
и
пересекаются в точке
. Докажите, что
лежит на серединном перпендикуляре к отрезку
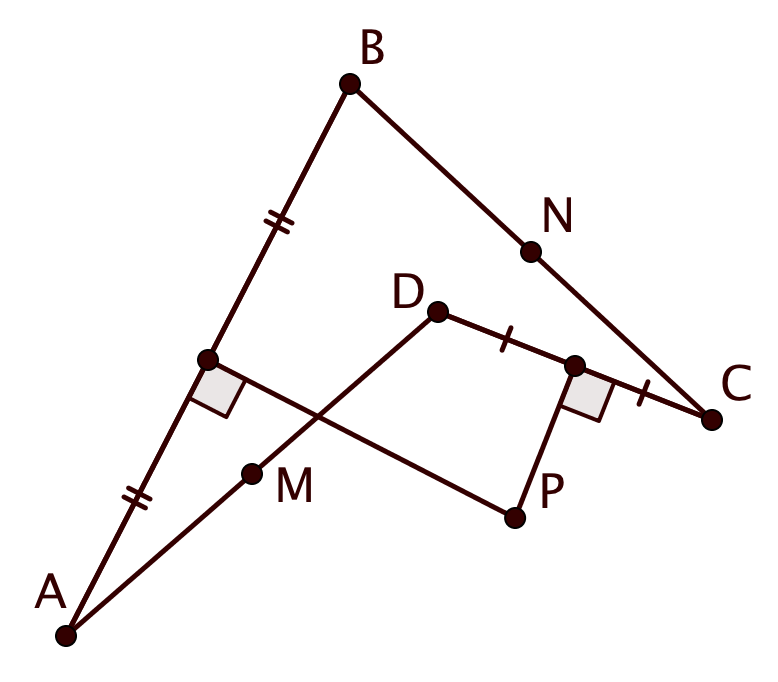
Так как точка лежит на серединном перпендикуляре к
, то
. Аналогично так как точка
лежит на серединном
перпендикуляре к
, выполнено
. Кроме того, по условию
. Поэтому
по трем сторонам. Отсюда
как соответствующие элементы равных треугольников. Эти же углы равны соответственно
и
. Также
как половины равных сторон
и
. Поэтому треугольники
и
равны по двум сторонам
,
и углам
. Значит,
как соответствующие элементы равных треугольников. Это и означает, что
лежит на серединном перпендикуляре к
.
Замечание. Использование серединных перпендикуляров к отрезкам и
как ГМТ вместо привычного равенства треугольников
позволяет избавиться от рассмотрения различных случаев картинки. В приведенном решении как раз от расположения точки
ничего не
зависит.
Ошибка.
Попробуйте повторить позже
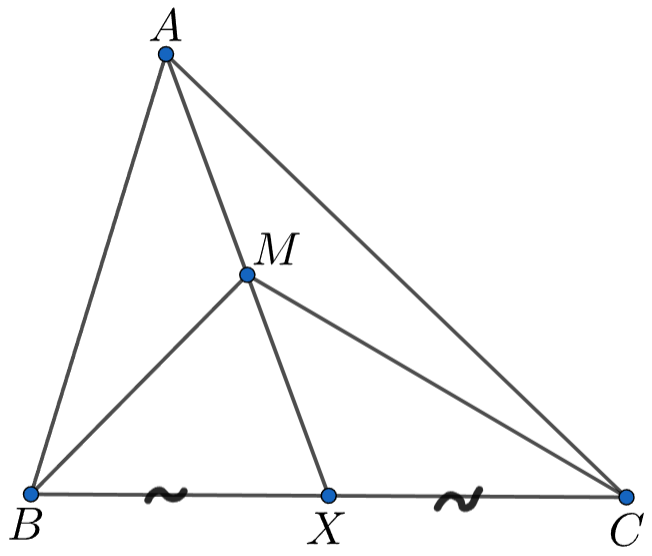
(a) Если записать площади по формуле через синусы, то мы получим равенство: Приведём
равенства к следующему виду:
. Мы знаем, что по теореме синусов
Продлим
до пересечения с
в точке
Тогда получаем, что
Перепишем это равенство так:
По теореме синусов левая
часть последнего равенства равна
а правая —
Значит,
то есть все такие точки
лежат на медиане треугольника,
проведённой к
Чтобы доказать, что для любой точки на медиане справедливо равенство равенство
достаточно проделать эти же
рассуждения, но в обратном порядке, исходя из равенства
(b) Проведём медиану отметим на ней такую точку
то
Нетрудно видеть, что
Следовательно,
а значит по рассуждениям из предыдущего пункта точка
лежит одновременно на всех
медианах треугольника
(c) Рассуждения аналогичны первому пункту, но в некоторых случаях надо дополнительно использовать, что синусы смежных углов равны.
Ошибка.
Попробуйте повторить позже
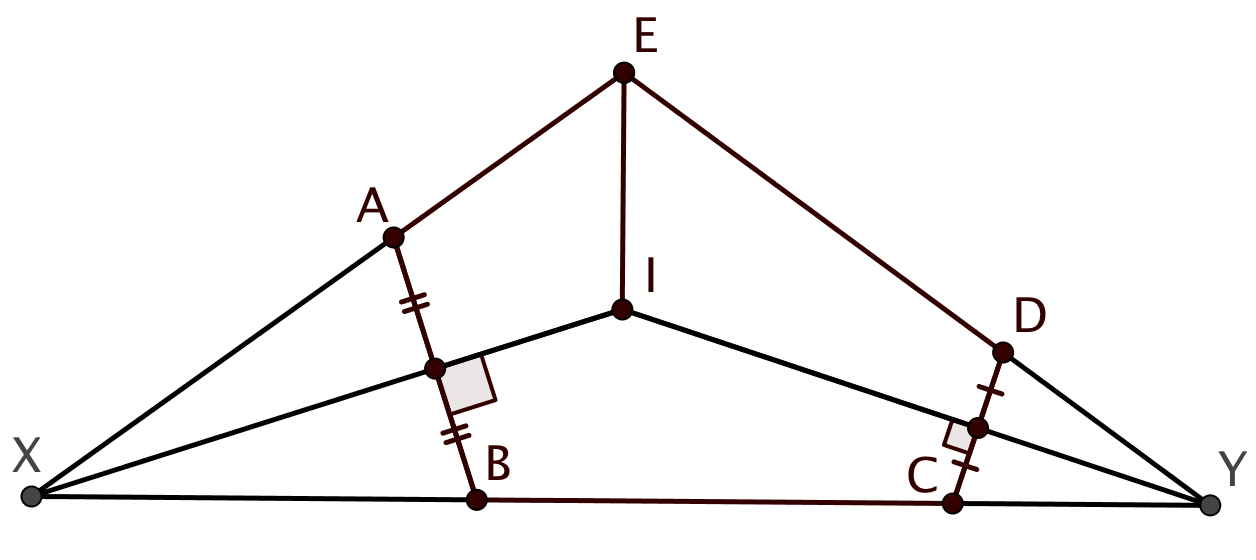
Из точек и
, лежащих на разных сторонах угла с вершиной
, восставлены перпендикуляры к сторонам, пересекающие
биссектрису угла в точках
и
соответственно. Докажите, что середина отрезка
равноудалена от точек
и
Опустим из точки перпендикуляр
на
, а также из точки
перпендикуляр
на
.
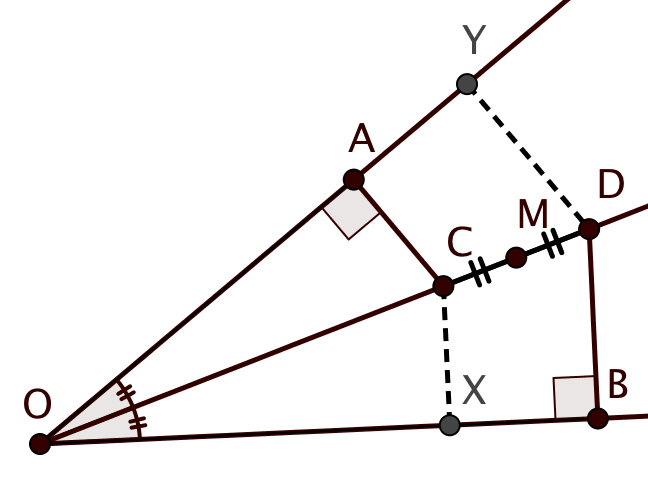
Рассмотрим четырехугольник . Это прямоугольная трапеция, так как
и
перпендикулярны
. Поэтому средняя
линия этой трапеции также перпендикулярна
и проходит через точку
. Более этого, эта средняя линия также является серединным
перпендикуляром к
. Поэтому точка
равноудалена от
и
. Аналогично получаем, что
равноудалена от
и
. Но
точки
и
симметричны относительно биссектрисы угла
, поэтому
, а значит точка
равноудалена от всех
четырех точек
,
,
и
. В частности,
Ошибка.
Попробуйте повторить позже
Докажите, что биссектрисы углов треугольника пересекаются в одной точке. Эта точка называется центром вписанной окружности.
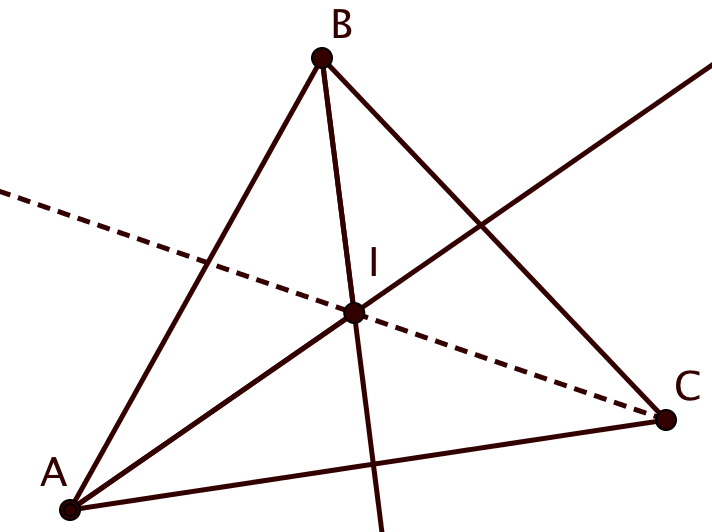
Проведем биссектрисы углов и
и обозначим точку их пересечения через
. Тогда по свойству биссектрисы как
ГМТ, точка
, так как она принадлежит биссектрисе угла
, равноудалена от прямых
и
и, так как точка
принадлежит биссектрисе угла
, равноудалена от прямых
и
. Но тогда указанная точка
равноудалена от всех трех
прямых, значит, равноудалена от сторон
и
угла
, и по признаку биссектрисы лежит на биссектрисе угла
. Таким образом, точка
принадлежит всем трем биссектрисам, значит, эти три биссектрисы пересекаются в одной
точке.
Точно так же доказывается, например, что серединные перпендикуляры к трем сторонам треугольника пересекаются в одной точке.
Если предыдущие рассуждения вызывают трудности, попробуйте доказать это сами.
Ошибка.
Попробуйте повторить позже
Докажите, что ГМТ, равноудаленных от сторон данного угла и лежащих внутри данного угла, есть биссектриса данного угла.
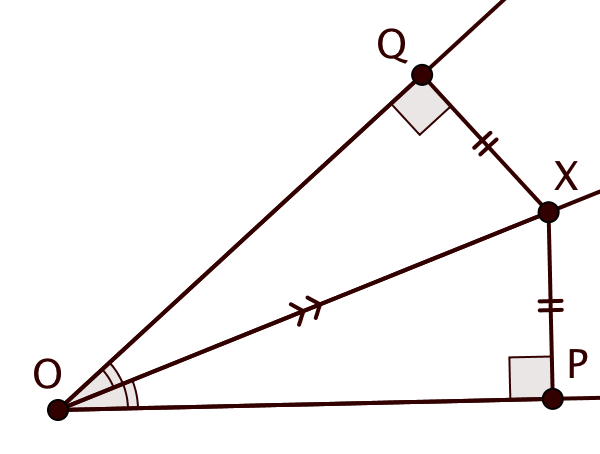
Сначала докажем, что любая точка биссектрисы обладает указанным свойством. Обозначим вершину угла через , а
произвольную точку на биссектрисе через
. Опустим из
перпендикуляры
и
на стороны угла. Так как
—
биссектриса
, то
. Поэтому, у прямоугольных треугольников
и
равны углы и общая
гипотенуза. Значит,
. В равных треугольниках соответствующие элементы равны, значит,
. Таким
образом, расстояния от произвольной точки
до сторон угла равны, значит, все точки биссектрисы равноудалены от сторон
угла.
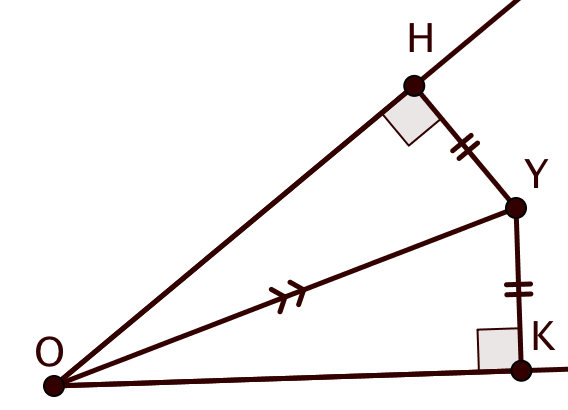
Теперь докажем, что любая точка, обладающая указанным свойством, лежит на биссектрисе. Рассмотрим произвольную точку ,
равноудаленную от сторон угла. Опустим из нее на стороны угла перпендикуляры
и
. Из равноудаленности следует, что отрезки
. Поэтому прямоугольные треугольники
и
равны по общей гипотенузе и равным катетам. Значит,
соответствующие
, то есть точка
лежит на биссектрисе.
Обратите особое внимание на доказательство в обе стороны: мы доказываем как то, что любая точка биссектрисы равноудалена от сторон углов, так и то, что любая точка, равноудаленная от сторон угла, лежит на биссектрисе.
Доказательства лишь в одну сторону недостаточно: может так получиться, что, например, не все точки, подходящие под заданное
условие, принадлежат указанному геометрическому месту. Например, множество точек, равноудаленных от двух данных прямых (кроме
внутренней биссектрисы в этом случае еще подходит внешняя биссектриса), или множество точек для данных точек
и
таких, что
треугольник
— прямоугольный (кроме окружности, построенной на
как на диаметре, если мы не уточняем, какой именно угол
прямой, также подходят две перпендикулярные отрезку
прямые, проходящие через
и через
соответственно, более того, сами
точки
и
надо «выколоть»).
Ошибка.
Попробуйте повторить позже
На сторонах выпуклого четырёхугольника во внешнюю сторону построены прямоугольники. Оказалось, что все вершины этих
прямоугольников, отличные от точек
лежат на одной окружности. Докажите, что четырехугольник
—
вписанный.
Источники:
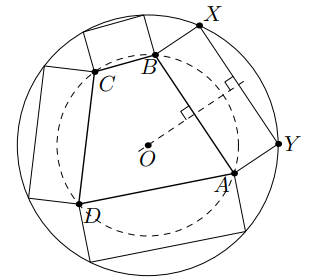
Пусть — один из данных прямоугольников, а
— центр окружности, на которой лежат восемь вершин из условия задачи.
Тогда
лежит на серединном перпендикуляре к отрезку
Но он совпадает с серединным перпендикуляром к отрезку
Поскольку
лежит на нём, имеем
Аналогично доказываем, что
и
Тогда
равноудалена от всех вершин четырехугольника
значит,
вписан в окружность с центром
что и требовалось
доказать.
Ошибка.
Попробуйте повторить позже
Даны две окружности, пересекающиеся в точках и
– произвольная точка одной из окружностей, отличная от
и
–
вторые точки пересечения прямых
с другой окружностью. Найдите геометрическое место центров окружностей, описанных около
треугольников
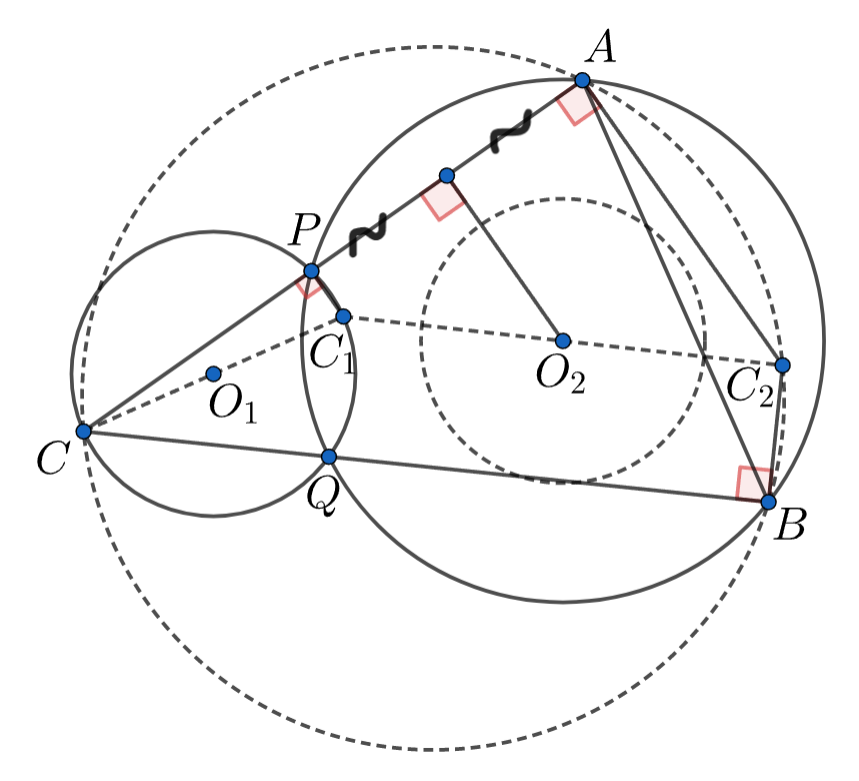
Пусть — точка, диаметрально противоположная
— точка, симметричная
относительно центра
второй окружности.
Тогда, так как
а проекцией
на
является середина отрезка
Аналогично,
Значит,
центром описанной около
окружности будет середина отрезка
При этом
параллелен отрезку между
центрами окружностей и вдвое его длиннее. Следовательно, искомым ГМТ будет окружность, полученная из той, на которой
лежит точка
переносом на вектор, определяемый центрами данных окружностей, без точек, соответствующих
и
Ошибка.
Попробуйте повторить позже
Найти геометрическое место середин отрезков с концами на двух различных непересекающихся окружностях, лежащих одна вне другой.
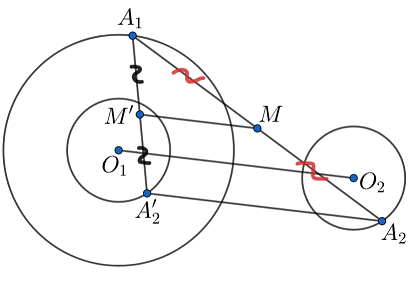
Пусть и
— данные окружности,
и
— их центры. Рассмотрим окружность
которая получается из окружности
параллельным переносом на вектор
центр этой окружности совпадает с центром окружности
Пусть
— точка окружности
и
— точки окружностей
и
соответствующие друг другу. Если
— середина отрезка
а
— середина
отрезка
то
Поэтому можно рассмотреть случай, когда даны две концентрические окружности, потому что
полученное ГМТ можно сдвинуть на вектор
Пусть — общий центр двух окружностей радиусом
и
причём
Фиксируем на окружности радиуса
точку
и
рассмотрим середины всех отрезков
где точка
перемещается по окружности радиуса
Они образуют окружность
(в этом можно убедиться, если сделать гомотетию в
с коэффициентом
тогда все середины попадут на большую
окружность), причём её самая близкая к
точка находится на расстоянии
а самая далёкая — на расстоянии
Если
точка
будет двигаться по всей окружности, то мы получим кольцо с внутренним радиусом
и внешним радиусом



