Ошибка.
Попробуйте повторить позже
Пункт a), подсказка 1
Давайте упорядочим наши числа! Тогда можно составить достаточное количество таких наборов чисел, что между любыми двумя наборами мы сможем точно поставить знак больше или меньше. Попробуем построить такой набор!
Пункт a), подсказка 2
Такс, очевидно, так как мы упорядочили наши числа, то мы можем сказать, что первое меньше второго, второе меньше третьего и так далее. А если к каждому из чисел(кроме последнего) прибавить максимальное число? Что можно сказать про такой набор чисел, каждое из которых состоит из двух слагаемых?
Пункт a), подсказка 3
Верно, эти числа тоже будут идти по возрастанию! То есть, знаки в таком наборе будут полностью совпадать со знаками в первом наборе, поэтому он тоже будет возрастающим(но в нём не будет последнего числа). Аналогично, дальше мы можем прибавлять максимум из оставшихся чисел к каждому числу из набора и тем самым получать новый набор! Сколько всего чисел тогда будет, если в первом наборе n, во втором n-1, в третьем n-2..,?
Пункт a), подсказка 4
Да, всего чисел будет n*(n-1)/2. Остаётся привести пример, когда все другие суммы, которые мы не рассматривали будут совпадать с хотя бы одним из рассмотренных нами чисел(для этого стоит располагать все n чисел компактно по отношению друг к другу)
Пункт b), подсказка 1
Представим, что все-все суммы будут различны. Как тогда удобно представлять каждую из сумм?
Пункт b), подсказка 2
Верно, тогда удобно считать, что каждое из чисел либо есть в сумме, либо его нет! То есть, на каждое число существует 2 варианта! Сколько всего вариантов, в таком случае?
Пункт b), подсказка 3
Да, таких сумм всего 2ⁿ - 1. Вычитаем единицу, потому что невозможен вариант, когда мы не взяли в сумму ни одного числа. Остается привести пример, когда такое возможно, для этого попробуйте взять числа на достаточно большом расстоянии друг от друга или чтобы каждое из чисел влияло только на одну цифру в сумме!
Можно считать, что исходные положительные числа расположены в порядке возрастания: Рассмотрим
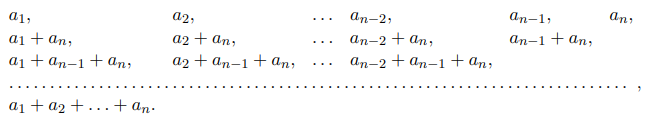
Очевидно, что здесь каждое число больше предыдущего, поэтому все выписанные числа различны. Их количество
соответствует требованиям задачи.
Осталось привести пример, в котором больше, чем различных сумм получить не удастся. Для этого подойдет набор из первых
натуральных чисел, из которых нельзя составить больше, чем
различных сумм: эти суммы - все натуральные числа от
до
б) Каждое число входит или не входит в рассматриваемую сумму. Кроме того, нужно ещё исключить сумму, не содержащую ни
одного слагаемого, поэтому различных сумм из
слагаемых можно составить не более, чем
Числа дают пример
различных чисел, из которых можно образовать наибольшее число различных сумм. Сумма
любых
чисел этого набора - это число, в десятичной записи которого используются только
и
Каждая такая сумма может быть
представлена в виде
-элементного упорядоченного набора из
и
Поскольку на каждом месте набора могут быть только две цифры,
их общее количество равно
Единственный невозможный набор, составленный из
нулей, необходимо исключить,
поэтому общее количество допустимых наборов равно
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное обучение
в Школково
Для детей ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Брянской областей, а также школьникам, находящимся в пунктах временного размещения Крыма обучение на платформе бесплатное.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ или олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




