Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде сторона основания
равна 12, а боковое ребро
равно
Через вершину
проведена плоскость
перпендикулярная прямой
и пересекающая ребро
в точке
а) Докажите, что плоскость делит высоту
пирамиды
в отношении
считая от вершины
б) Найдите расстояние между прямыми и
а) Прямая так как
принадлежит плоскости
перпендикулярной
Пусть
пересекает
в точке
тогда нам нужно доказать, что
Рассмотрим треугольник Его сторона
равна
как диагональ квадрата со стороной 12. Получили,
что
Следовательно, треугольник равносторонний. Поскольку
и
— его высоты, а значит, и медианы, то медиана
делит медиану
в отношении
считая от точки
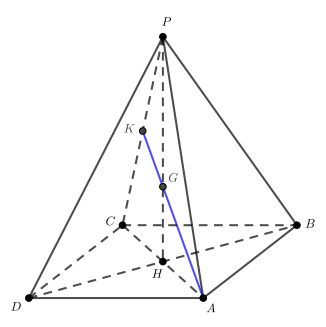
б) Отрезок является проекцией отрезка
на плоскость основания. Пусть
— проекция середины
отрезка
на основание пирамиды. Тогда
— середина
и
откуда
Из этого следует, что прямая
параллельна плоскости
Таким образом, расстояние между прямыми и
равно расстоянию между прямой
и плоскостью
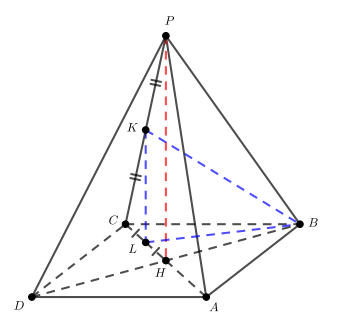
Рассмотрим высоту из вершины
треугольника
Имеем
а также
перпендикулярна прямым
(так как
и
плоскости
Тогда длина
— это и есть расстояние между прямой
и плоскостью
Далее имеем:
Тогда по теореме Пифагора для прямоугольного треугольника
Значит, окончательно из прямоугольного треугольника
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основанием прямой треугольной призмы является прямоугольный треугольник
причем
Диагонали
боковых граней
и
равны 26 и 10 соответственно,
а) Докажите, что — прямоугольный.
б) Найдите объем пирамиды
а) Так как
то по теореме о трех перпендикулярах
Следовательно,
—
прямоугольный.
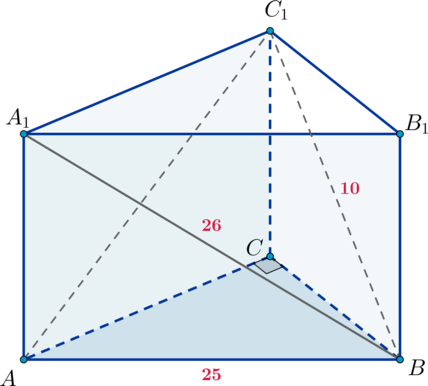
б) Заметим, что и
следовательно, по признаку перпендикулярности прямой и плоскости
Следовательно,
— высота пирамиды
с основанием
Так как — прямоугольный, то
По теореме Пифагора имеем:
Тогда искомый объем равен

б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Каждую вершину тетраэдра симметрично отразили относительно точки
пересечения медиан противолежащей грани. Пусть
— точки,
симметричные точкам
и
соответственно.
а) Докажите, что отрезки
и
пересекаются в одной
точке.
б) Найдите отношение объемов тетраэдров и
а) Пусть
и
— середины ребер
и
соответственно,
— точки пересечения медиан граней
и
соответственно.
Рассмотрим плоскость в которой лежат точки
и
Проведем прямые
и
и отметим на них точки
и
соответственно так, чтобы
и
были серединами отрезков
и
Пусть
Так как по свойству медиан
то по теореме Менелая для треугольника
и секущей
имеем:
Так как каждый из отрезков
и
определен одним и тем же
образом, то получаем, что отрезки
и
тоже делят отрезок
в
отношении
то есть проходят через точку
Что и требовалось
доказать.
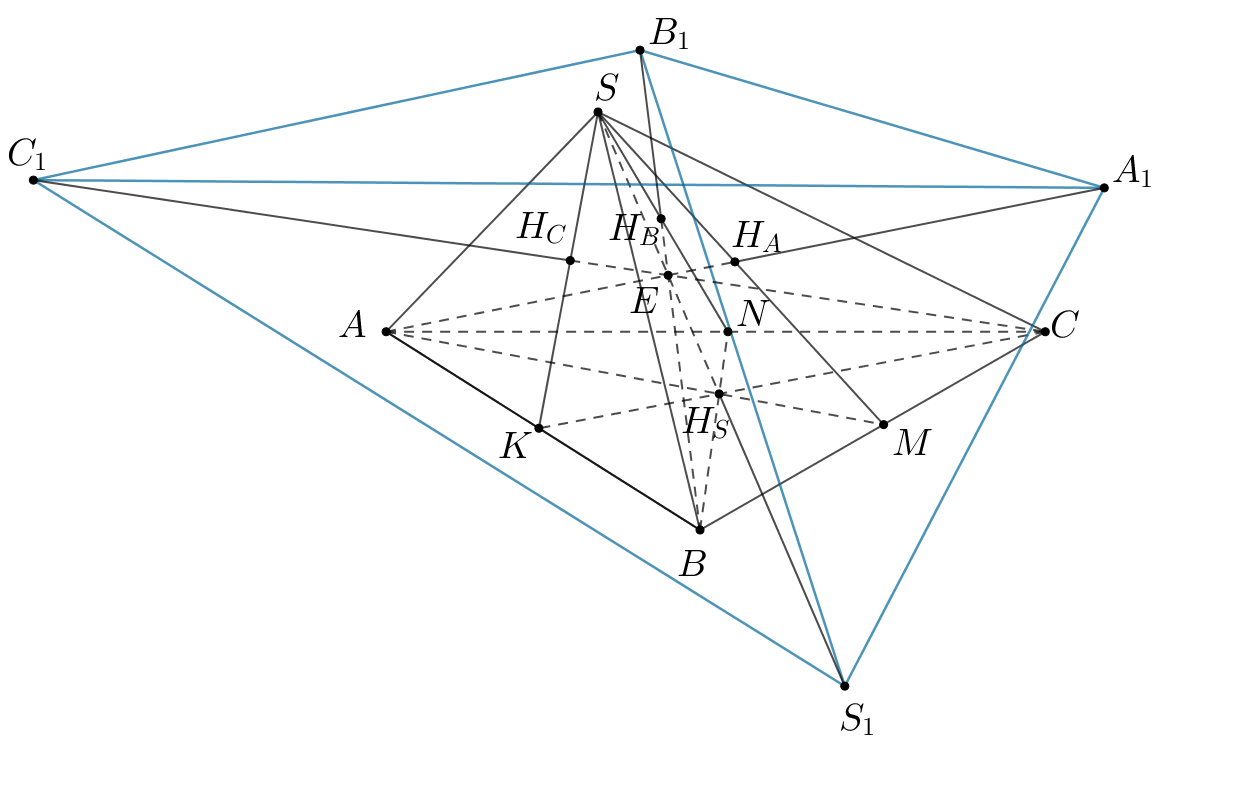
б) По теореме Менелая, поступая, как в пункте а), получаем
Тогда
Заметим, что следовательно
Аналогично получаем, что
Значит, с коэффициентом подобия
Пусть
— перпендикуляры к плоскости
Так как
то
Так как
то
Для точек
и
все аналогично. Тогда
Это значит, что точки
и
находятся на одинаковом расстоянии от
плоскости
следовательно,
и расстояние между ними
равно
Пусть Тогда так как
то получаем
Следовательно, если
— длина перпендикуляра, опущенного из
на
то
Тогда
б)
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде с вершиной
через точку
параллельно прямой
проведена плоскость
а через прямую
параллельно плоскости
проведена плоскость
так, что сечения пирамиды
этими плоскостями равновелики.
а) Докажите, что плоскости и
разбивают ребро
на три равные
части.
б) Известно, что сторона основания пирамиды равна
а высота
равна 8. Найдите расстояние между плоскостями
и
а) Пусть пересекает
в точке
Обозначим за
точку пересечения
и
Так как
то
пересечет плоскость
по
прямой, параллельной
и проходящей через
Проведем отрезок
через
Тогда
— сечение пирамиды плоскостью
Так как то секущая их плоскость
пересечет их по параллельным
прямым. Следовательно, плоскость
проходит через прямую
Получили сечение
пирамиды плоскостью
По условию
По теореме о трех перпендикулярах (
) имеем
Так как
то
Следовательно,
Так как и
то
Значит,
Отсюда имеем:
Тогда по теореме Фалеса для и из подобия треугольников:
Следовательно, можно принять
откуда
Тогда
Что и требовалось доказать.
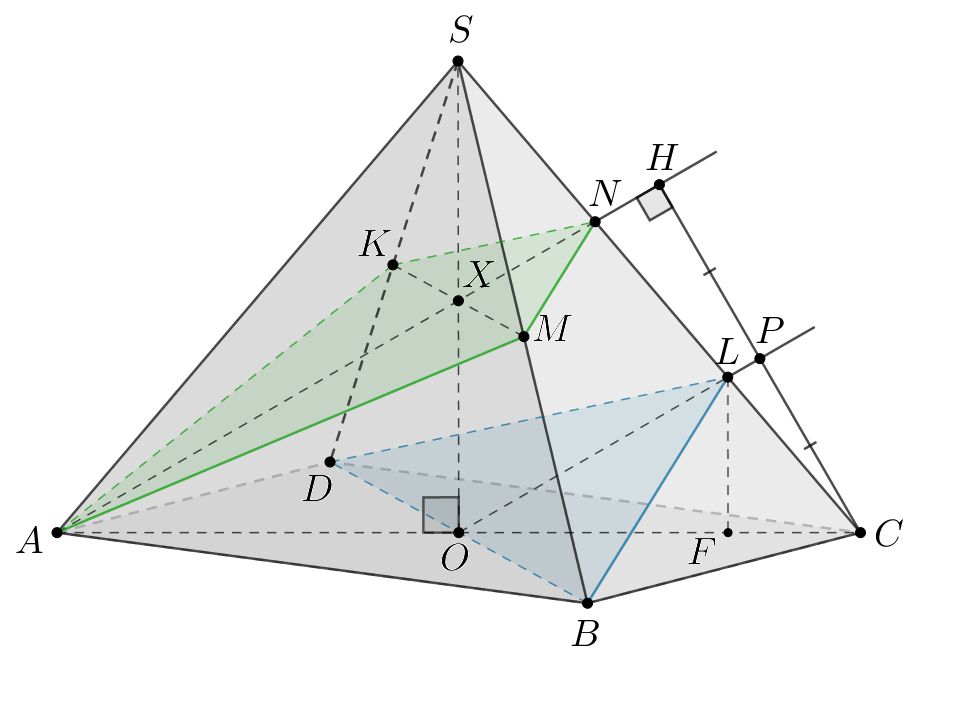
б) следовательно,
перпендикулярна любой прямой из этой
плоскости. Проведем
тогда с учетом
получаем, что
Пусть
Тогда
— искомое расстояние.
По теореме Фалеса, так как
имеем
Будем искать
Рассмотрим пирамиду Пусть
Тогда имеем:
Из подобия имеем
Так как
и
то
Значит, по теореме Пифагора
Тогда
б) 2,4
Ошибка.
Попробуйте повторить позже
Диагонали и
основания
правильной шестиугольной призмы
пересекаются в точке
а диагонали
и
боковой грани
пересекаются в точке
a) Докажите, что прямая параллельна плоскости
б) Найдите расстояние между прямой и плоскостью
если
сторона основания призмы
равна
а её высота
равна 4.
Источники:
а) Так как то плоскость
(будем называть ее
)
пересечет нижнее основание призмы по прямой
Следовательно,
—
сечение призмы плоскостью
Рассмотрим в нем лежат
и
Докажем, что
Отсюда последует, что
так как
Так как — прямоугольник, то
— середина его диагонали
Рассмотрим нижнее основание призмы. Так как
делит угол
пополам,
то
— биссектриса в равнобедренном
проведенная к основанию,
значит, она же и медиана, то есть
— середина
Таким образом, — средняя линия в
следовательно,
и
Что и требовалось доказать.
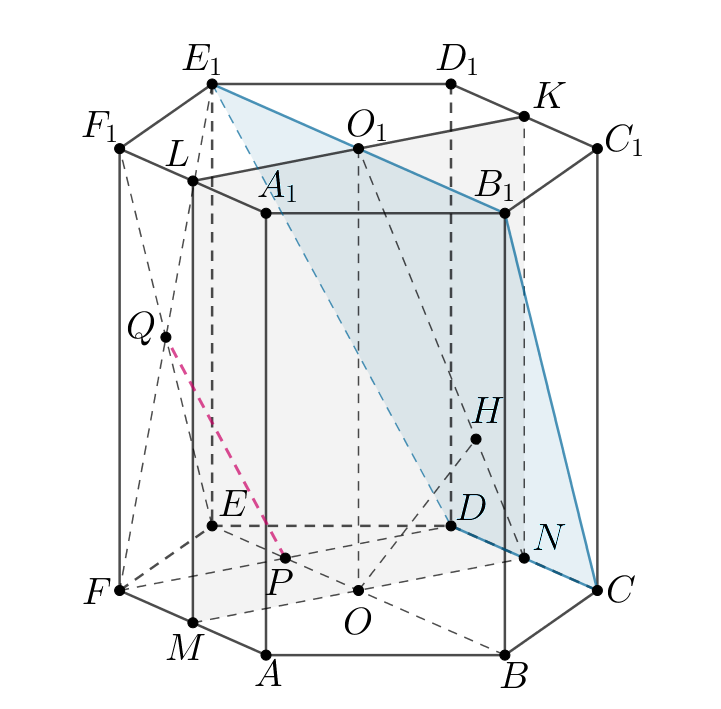
б) Так как то искомое расстояние равно
где — произвольная точка прямой
Выберем для поиска расстояния
точку
Заметим, что лежит на прямой
параллельной
следовательно,
где — произвольная точка прямой
Таким образом, расстояние от
до
равно расстоянию от точки
до
Выберем точку как середину отрезка
Пусть также
— середины
и
соответственно. То есть
Так как прямая параллельна боковому ребру призмы, то она
перпендикулярна основаниям призмы. Так как по свойству правильного
шестиугольника
то по теореме о трех перпендикулярах
следовательно,
Также
Следовательно,
перпендикулярна плоскости, построенной на прямых
и
—
плоскости
которая сечет призму по четырехугольнику

Проведем Учитывая, что
получаем, что
Следовательно,
так как
Таким образом, длина — искомое расстояние
Точка — середина отрезка
равного
следовательно, пользуясь
теоремой косинусов для равнобедренного
с углом против основания
Заметим, что и
— середины б´ольших диагоналей правильных
шестиугольников, следовательно, это их центры. Тогда
параллельна
боковому ребру призмы, то есть перпендикулярна основаниям, и равна боковому
ребру, то есть высоте призмы (ведь призма правильная).
Получили прямоугольный в котором к гипотенузе проведена высота
Она равна
б) 2,4
Ошибка.
Попробуйте повторить позже
— тетраэдр, в котором
площади граней
и
равны.
а) Докажите, что отрезок, соединяющий середины ребер и
является
их общим перпендикуляром.
б) Найдите расстояние между ребрами и
если оно больше 4 и
известно, что
а объем тетраэдра
равен
42.
а) Пусть Так как
то
следовательно,
Так как
то
По теореме Пифагора
Таким образом, мы получили, что — середина
Таким образом, равнобедренный, откуда медиана
также
является и высотой. Следовательно,
также
(так как
а
). Следовательно,
— общий перпендикуляр
прямых
и
Чтд.
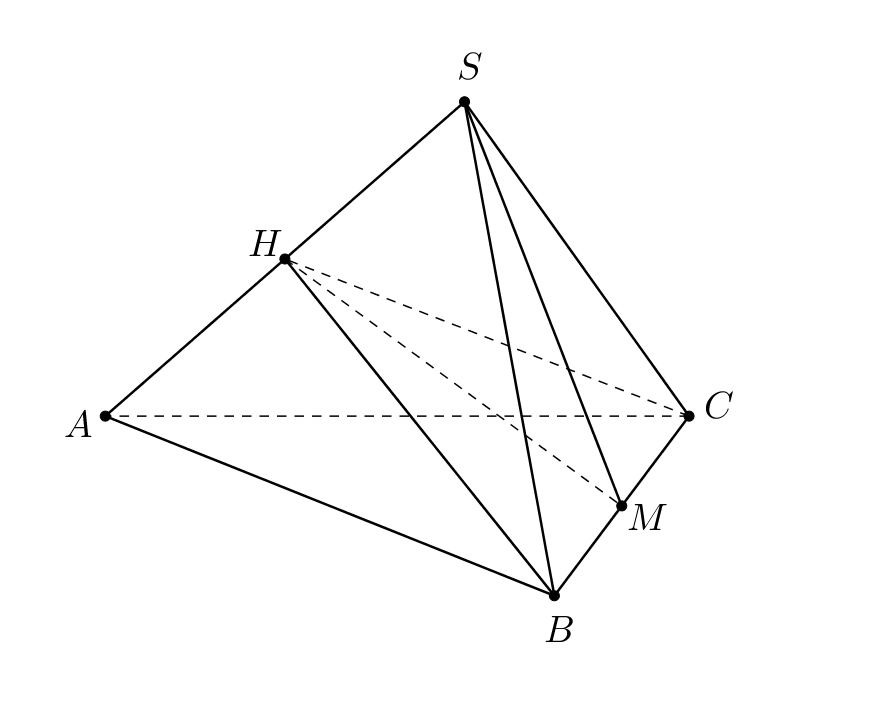
б) — есть расстояние между скрещивающимися прямыми
и
Пусть
Тогда
Из пункта а) следует, что
По теореме Пифагора
Получаем систему
Так как по условию расстояние больше 4, то оно равно 5,25.
б) 5,25
Ошибка.
Попробуйте повторить позже
На ребре куба
взята точка
такая, что
а) Докажите, что плоскость перпендикулярная прямой
и содержащая
делит ребро
на отрезки
и
отношение которых равно
б) На диагонали грани
взята точка
— середина этой
диагонали. Найдите расстояние между скрещивающимися прямыми
и
если ребро куба равно
а
а) Заметим, что следовательно,
Проведем через
точку
прямую
Тогда
перпендикулярна
двум пересекающимся прямым
и
следовательно,
перпендикулярна
плоскости, построенной на этих прямых. Значит,
и
Пусть Тогда
следовательно,
Следовательно,
как
прямоугольные по острому углу и равным катетам
Следовательно,
Следовательно, так как по условию
то
откуда следует, что
то есть
Что и требовалось доказать.
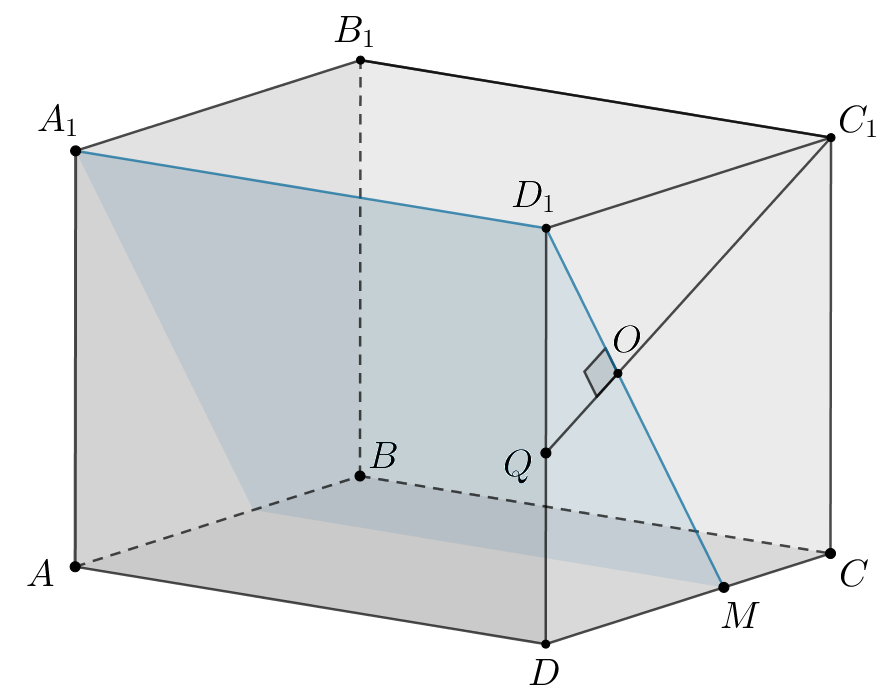
б) 1. Так как то можно принять
Тогда
— ребро куба.
Вспомним, что для того, чтобы найти расстояние между двумя скрещивающимися
прямыми и
нужно провести плоскость перпендикулярно прямой
спроецировать прямую
на эту плоскость и найти расстояние от точки
пересечения прямой
с этой плоскостью до проекции
прямой
(см. рис.)
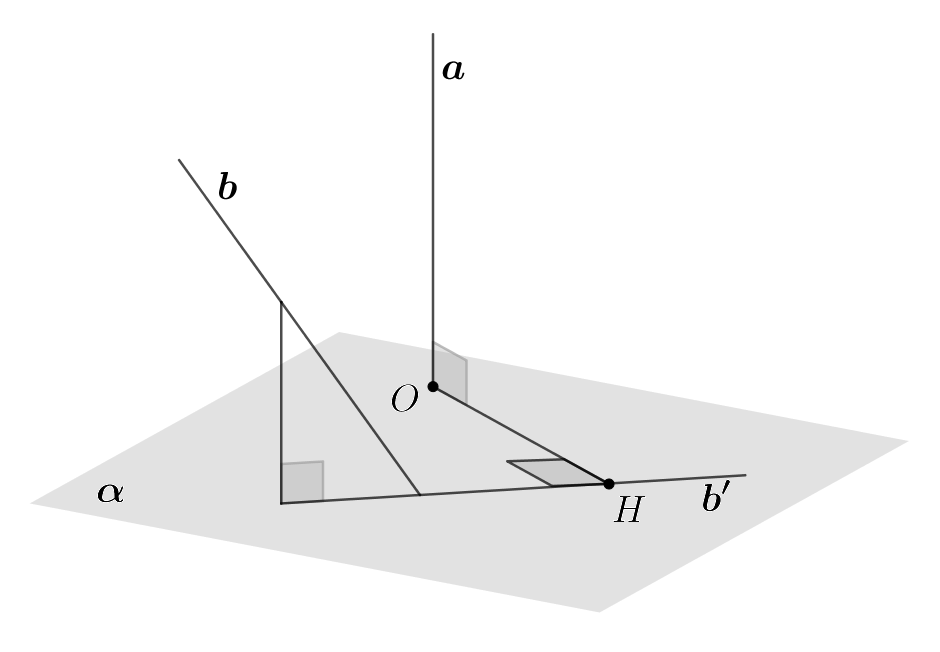
Из пункта а) следует, что плоскость, перпендикулярная прямой уже
найдена — это плоскость
Сечение куба этой плоскостью —
прямоугольник
(прямоугольник, так
как
следовательно,
а
).
Точка пересечения прямой с
— точка
2. Осталось найти проекцию прямой на
Для этого спроецируем точки
и
на нее.
Найдем проекцию на плоскость
Проведем
тогда
Пусть
значит,
— проекция
на
Заметим сразу, что
Найдем проекцию на плоскость
Проведем
следовательно,
а значит
Тогда
— проекция точки
на
Проведем
через точку
как показано на рисунке:
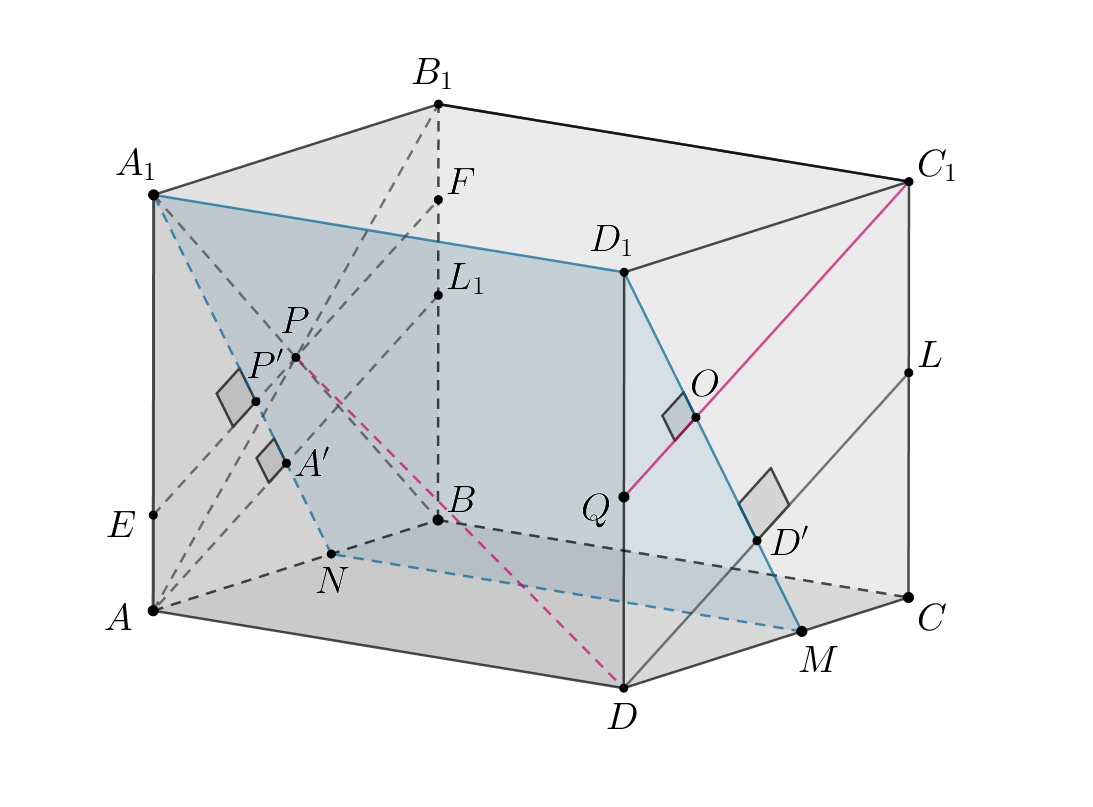
Тогда — проекция точки
на
3. Опустим перпендикуляр из точки на
Получим отрезок
Это
и есть искомое расстояние.
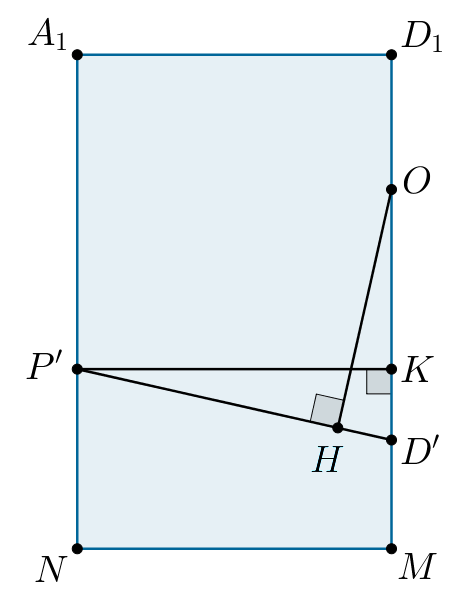
Заметим, что если то
как прямоугольные
по общему острому углу
Следовательно,
Необходимо выразить отрезки и
через
4. Найдем необходимые отношения.
Так как — середина
то по теореме Фалеса
— высота, опущенная из вершины прямого угла
следовательно,
Пусть Так как по свойству высоты из
прямого угла
то получаем квадратное относительно
уравнение:
Тогда

Заметим, что следовательно,
По теореме Фалеса
Заметим, что
как прямоугольные по двум катетам. Следовательно,
Тогда
Значит,
Так как — прямоугольник, то
следовательно,
Тогда по теореме Пифагора
5. Таким образом, мы нашли, что
значит,
Так как ребро куба равно то
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде
На ребрах
и
взяты соответственно точки
и
такие, что
а) Докажите, что общий перпендикуляр к прямым и
не имеет
общих точек с гранью
б) Найдите расстояние между прямыми и
а) Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный обеим прямым, концы которого лежат на этих прямых. Длина этого перпендикуляра равна расстоянию между скрещивающимися прямыми.
Проведем Тогда
(плоскость
— это
плоскость
), следовательно,
Поэтому
построим отрезок
один конец которого лежит на прямой
а другой — в
плоскости
так, чтобы этот отрезок был перпендикулярен
Тогда
этот отрезок будет параллелен общему перпендикуляру к
и
а длина
его будет равна длине общего перпендикуляра.
(Заметим, что плоскость пересекает параллелепипед по многоугольнику
)
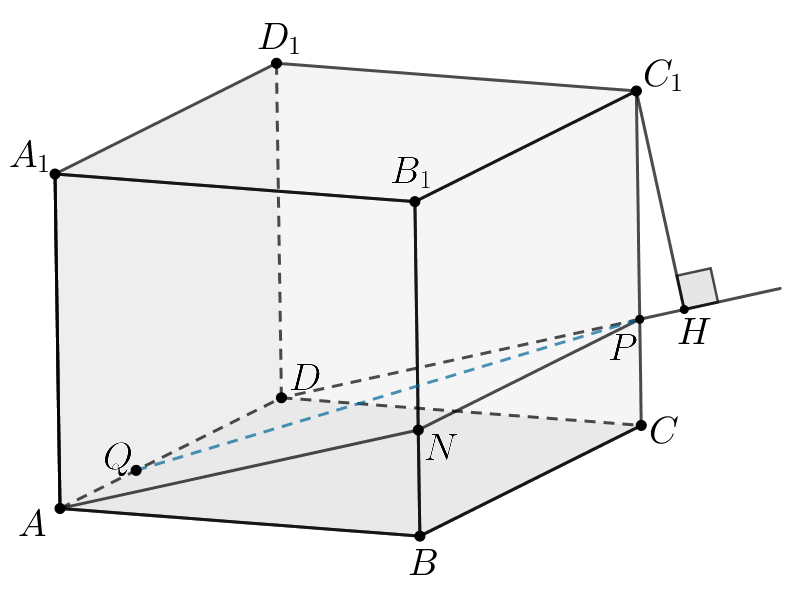
Пусть Так как
а
то
следовательно,
Тогда
и
следовательно,
следовательно,
Заметим, что
(так
как
), а общий перпендикуляр к
прямым
и
параллелен отрезку
Следовательно, этот общий
перпендикуляр параллелен грани
то есть не имеет с ней общих точек.
Что и требовалось доказать.
б) как прямоугольные по острому углу:
как вертикальные. Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В основании пирамиды с вершиной лежит прямоугольник
со
сторонами
и
Все боковые рёбра пирамиды равны
На
рёбрах
и
отмечены точки
и
соответственно так, что
Плоскость сечения проходит через точки
и
перпендикулярно ребру
а) Докажите, что плоскость сечения пересекает ребро в его середине.
б) Найдите расстояние от точки до плоскости сечения.
а)
1. Проведём диагональ и отрезок
которые пересекаются в точке
2. Рассмотрим и
как накрест лежащие,
как накрест
лежащие и
откуда
и
равны по двум углам и
стороне.
3. У равных треугольников равные соответствующие элементы, следовательно,
Это в свою очередь означает, что точка
— точка пересечения
диагоналей прямоугольника в основании, то есть принадлежит плоскости
сечения.
4. Рассмотрим прямоугольный По теореме Пифагора:
откуда
5. Рассмотрим По обратной теореме Пифагора:
откуда получаем, что
—
прямоугольный.
6. Провед̈eм Тогда
— средняя линия по определению, откуда
— середина ребра
7. поскольку
Следовательно, точка
также
принадлежит плоскоскости сечения, ведь эта плоскость перпендикулярна ребру
Ч.Т.Д.
![]()
Для профилактики доведём построение сечения до конца.
1. Продлим прямую до точки пересечения с прямой
— точки
Проведём отрезок
пересекающий
в точке
Проведём
2. Поскольку — прямоугольник, то длины противоположных сторон
равны, откуда
3. Рассмотрим и
и
— один и тот же угол, откуда
4. Из выявленного подобия выводим отношения отрезков:
5. Запишем теорему Менелая для и секущей
Теперь мы знаем положение всех вершин сечения и его построение полностью завершено.
б)
1.
Факт: расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на эту плоскость.
2. Заметим, что раз и
плоскости сечения, то
плоскости
сечения. То есть расстояния от каждой точки данной прямой до этой
плоскости одинаковы.
3. Таким образом, мы можем найти расстояние от точки до плоскости
сечения и автоматически найти ответ.
4. Поскольку ребро плоскости сечения, то
— перпендикуляр,
опущенный из точки
на плоскость сечения (то есть его длина равна искомому
расстоянию). Длина
равна половине длины ребра
(
— середина
),
то есть
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На ребре правильной призмы
боковое ребро
которой в два раза больше стороны основания, взята точка
такая, что
а на ребрах
и
взяты их середины — точки
и
соответственно.
а) Докажите, что прямая перпендикулярна плоскости
б) Найдите угол между прямой и плоскостью
а) Рассмотрим основание Пусть
Так как
то
Заметим, что
как прямоугольные по двум катетам. Следовательно,
Тогда, если
то
Следовательно,
Так как призма правильная, то следовательно,
Таким образом, прямая
перпендикулярна двум прямым
и
из
плоскости
значит,
Что и требовалось доказать.
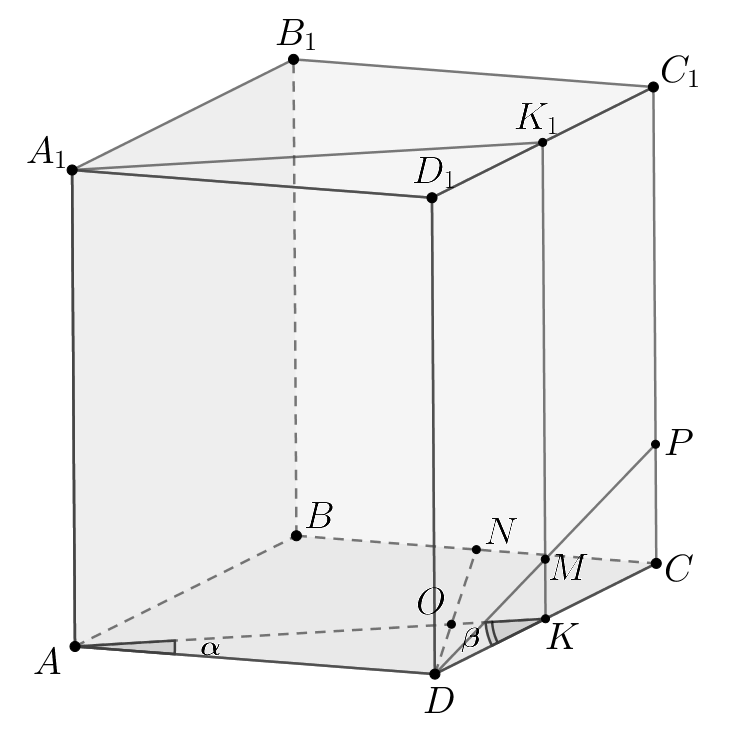
б) Пусть — проекция
на плоскость верхнего основания. Пусть
Так как
то
— проекция прямой
на
плоскость
Следовательно,
— угол между
прямой
и плоскостью
Его и нужно найти.
прямоугольный, следовательно,
Найдем эти
отрезки.
Из условия задачи следует, что
Так как
то по
теореме Фалеса
— середина
Следовательно,
По теореме
Пифагора
Следовательно,
— высота из прямого угла в
Следовательно,
Следовательно,
б)
Ошибка.
Попробуйте повторить позже
В правильной четырёхугольной пирамиде сторона основания
равна
боковому ребру
Медианы треугольника
пересекаются в точке
а) Докажите, что =
б) В треугольнике проведена медиана
Найдите площадь
треугольника
если
а)
![]()
1. Проведём медиану в
По свойству точки пересечения медиан в
треугольнике
2. Пирамида правильная, следовательно, все боковые ребра равны и все
стороны основания также равны. По условию
то есть
боковое ребро равно стороне основания, значит, вообще все ребра пирамиды
равны.
3. Обозначим длину за
В таком случае
4. равносторонний, следовательно
— это ещё и высота и
–
прямоугольный.
5. По теореме Пифагора для
6. Из пунктов 1) и 5) получаем, что
7. Проведём В основании пирамиды лежит квадрат, так как пирамида
правильная, поэтому
— прямоугольный.
8. По теореме Пифагора для
9. По теореме косинусов для найдём
10. По теореме косинусов для найдём
11. Таким образом, Ч.Т.Д.
б)
1. Раз — середина
то, помня об отношении
делаем вывод:
2. Опустим перпендикуляр на
В таком случае
—
прямоугольный.
3. и
— один и тот же угол, тогда по формуле косинуса для
4. По теореме Пифагора для
5. Помня вычисленные в пункте а) величины, находим, что
6. По формуле площади треугольника:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В правильной четырехугольной пирамиде с вершиной
боковое ребро
а высота пирамиды равна
Точки
и
— середины ребер
и
соответственно. В пирамиде
точка
является вершиной, а
— высотой пирамиды.
а) Докажите, что точка является серединой
б) Найдите расстояние между прямыми и
а)
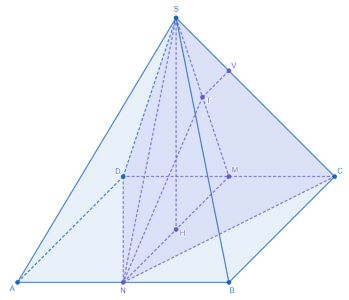
1. — высота пирамиды
значит,
и
в
частности.
2. Пирамида правильная, в её основании лежит квадрат.
Раз так, то очевидно, что
— прямоугольник, где
и
3. Более того, основание высоты пирамиды точка
— центр
основания, делящий отрезок
пополам.
4. Ну и в конце концов раз пирамида правильная, то боковые рёбра равны и
— равнобедренный, где
— высота и медиана одновременно.
5. — прямоугольный, в нём по теореме Пифагора:
6. — прямоугольный, в нём по теореме Пифагора:
Поскольку имеем:
7. В таком случае а
То есть
—
равнобедренный, где
— высота и медиана одновременно, а значит, точка
— середина
Ч.Т.Д.
б) Расстояние между двумя прямыми равно длине их общего перпендикуляра.
1. Если прямая перпендикулярна плоскости, то она перпендикулярна любой
прямой, лежащей в этой плоскости. Из приведённого тезиса следует, что
перпендикулярна любой прямой в плоскости
То есть чтобы построить искомый общий перпендикуляр, нам всего лишь
следует провести перпендикуляр из точки
на прямую
В таком случае по озвученному факту и
по
построению.
2. Найдём из подобия
поскольку
и
3. поскольку
— равнобедренный, где
— высота и
медиана одновременно.
4. Из подобия треугольников имеем следующие отношения их соответствующих сторон:
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В кубе точки
и
— середины ребер
и
соответственно.
а) Докажите, что прямые и
перпендикулярны.
б) Плоскость проходит через точки
и
параллельно прямой
Найдите расстояние от точки
до плоскости
если
а) Пусть
по двум катетам, следовательно,
Отрезок — проекция отрезка
на плоскость
Следовательно,
по теореме о трех перпендикулярах
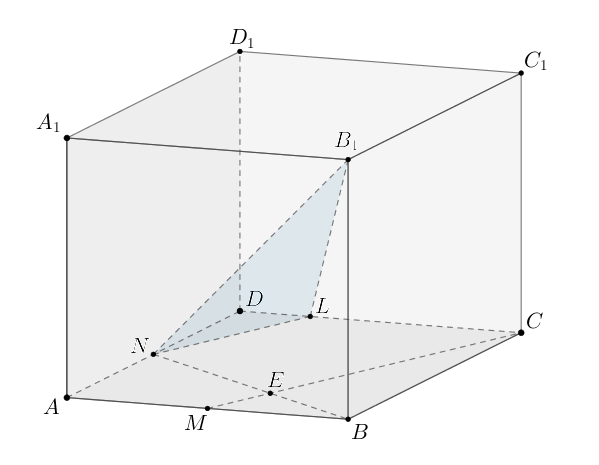
б) Пусть Прямые
так как
и
пересечет
плоскость, в которой лежит
по прямой, параллельной
Следовательно,
а значит, прямоугольные
по
острому углу. Получаем:
Пусть
Получаем:
Тогда
Запишем объем пирамиды двумя способами:
б) 2
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде на диагонали
отмечена точка
так, что
Точка
— середина отрезка
а) Докажите, что прямая проходит через точку
б) Найдите объем параллелепипеда если длина
отрезка
равна расстоянию между прямыми
и
и равна
а) — точка пересечения диагоналей прямоугольника
следовательно,
как и
и
(
,
). Следовательно,
Следовательно, точки
и
лежат на одной прямой. Чтд.
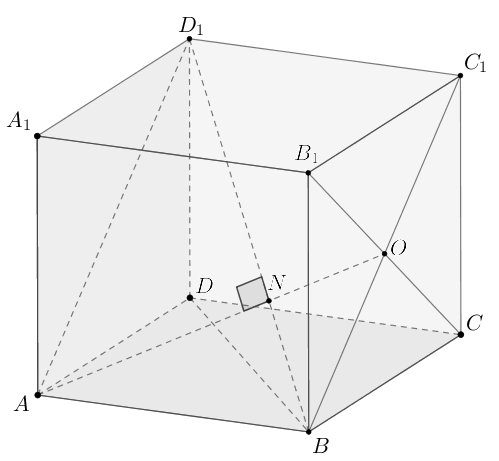
б) и
— скрещивающиеся прямые. Так как отрезок
равен
расстоянию между ними, то
перпендикулярен обеим этим прямым.
Следовательно,
так как
и
Следовательно,
диагонали прямоугольника
взаимно перпендикулярны, значит, он
является квадратом.
Из следует, что
Следовательно, по свойству высоты прямоугольного треугольника, проведенной к
гипотенузе, имеем
Также
Значит, Таким образом, в прямоугольном
параллелепипеде
все ребра равны 6, то есть он является кубом.
Тогда его объем равен 216.
б) 216
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида в основании которой лежит
прямоугольник
а основание высоты пирамиды — центр этого
прямоугольника. Точка
— середина ребра
точка
лежит на ребре
Через точки
и
проведена плоскость
параллельная ребру
и
пересекающая ребро
в точке
а) Докажите, что
б) Найдите отношение объемов многогранников, на которые плоскость делит
пирамиду
если
а) Если — точка пересечения диагоналей прямоугольника
то
—
высота пирамиды
(по условию). Так как
то по обратной теореме Фалеса
следовательно,
Пусть Тогда
(
как вертикальные,
как накрест лежащие при прямых
). Следовательно,
Следовательно,
Так как то
пересечет плоскость
в которой лежит
по
прямой
параллельной
(
). По теореме Фалеса
Чтд.
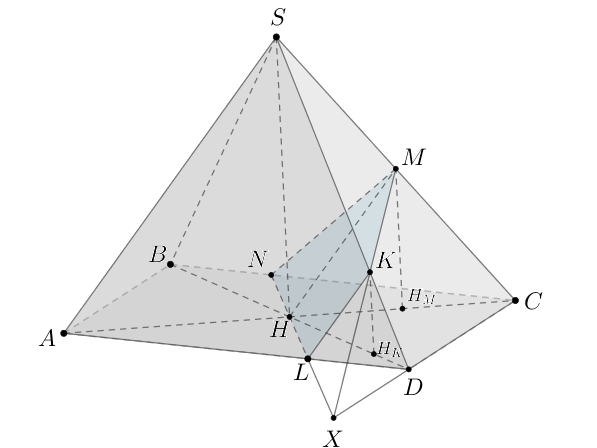
б) Будем искать объем многогранника
как разность объемов
треугольных пирамид
и
где
— точка пересечения прямых
и
Так как то
Тогда, так как
имеем
— середина
Пусть
и
Тогда

Проведем перпендикуляры и
на плоскость
Докажем лемму: если — наклонная к плоскости
,
— точка на
,
,
, то
. Действительно,
,
так как
и эти прямые задают плоскость
. Тогда
как прямоугольные с общим углом
.
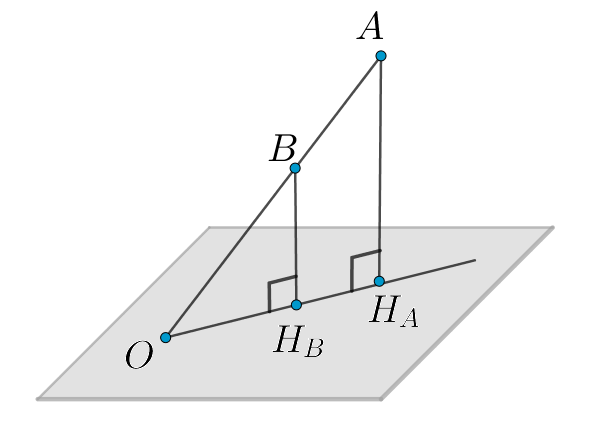
Тогда, если то
Следовательно,
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида в основании которой лежит
параллелограмм
На ребрах
и
отмечены точки
и
соответственно так, что
а) Докажите, что плоскость делит ребро
в отношении
считая от точки
б) Найдите отношение объемов многогранников, на которые плоскость
разделила пирамиду
а) Назовем плоскость плоскостью
Пусть прямые
и
пресекаются в точке
Тогда
— точка пересечения
с ребром
Требуется доказать, что
следовательно,
По теореме Менелая для и прямой
получаем
Чтд.
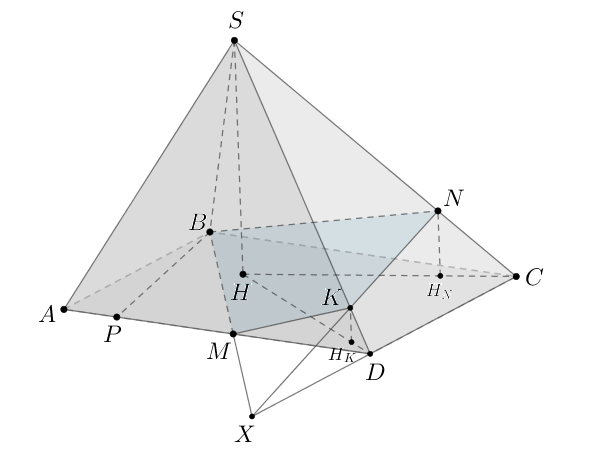
б) Найдем объем многогранника
как разность объемов
треугольных пирамид
и
Проведем перпендикуляры
и
на плоскость
Докажем лемму: если — наклонная к плоскости
,
— точка на
,
,
, то
. Действительно,
,
так как
и эти прямые задают плоскость
. Тогда
как прямоугольные с общим углом
.
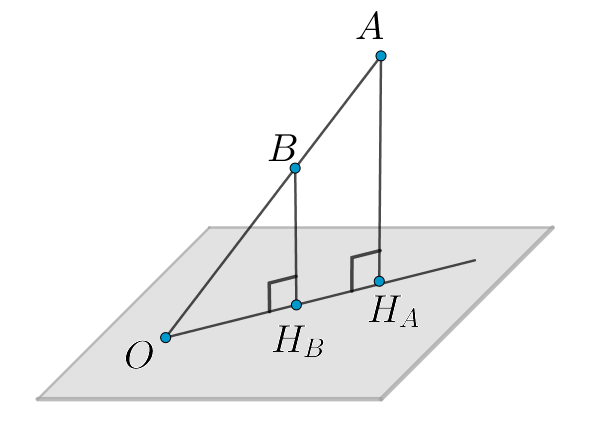
Тогда, если то
Пусть также
Тогда
Следовательно,
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида в основании которой лежит
прямоугольник
а боковые ребра пирамиды равны диагонали основания.
Точки
и
отмечены на ребрах
и
соответственно так, что
а) Докажите, что плоскость параллельна ребру
б) Найдите площадь сечения пирамиды плоскостью
если
боковое ребро пирамиды равно 24,
а угол между диагоналями
основания равен
а) Пусть Рассмотрим грань
По теореме Менелая для
и прямой
получаем
Далее, как прямоугольные по общему острому
Следовательно,
Тогда по обратной теореме Фалеса Так как
по
построению, то
Что и требовалось доказать.
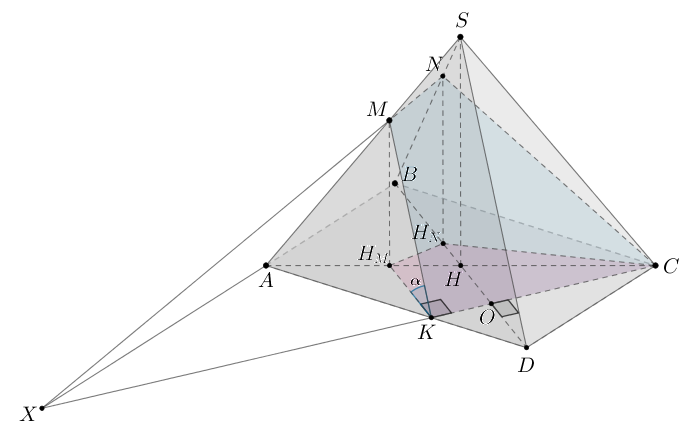
б) Так как боковые ребра пирамиды равны, то основание высоты
пирамиды — центр описанной около основания
окружности, то есть точка
пересечения диагоналей прямоугольника
Сечение пирамиды
плоскостью
— четырехугольник
Будем искать его площадь по
формуле
Здесь — угол между плоскостью сечения и плоскостью проекции.
Спроецируем четырехугольник на плоскость
Опустим
перпендикуляры
и
на эту плоскость. Тогда по теореме
Фалеса
Следовательно,
Так как то
Следовательно, — середина отрезка
Тогда, так как
правильный, то
— медиана и высота этого треугольника. Следовательно,
то есть
Так как то

Заметим, что
Отсюда по обратной теореме Фалеса следует, что Следовательно,
а
откуда
Тогда имеем:
Следовательно,
Также имеем:
Следовательно,

Так как
— линия пересечения плоскостей
и
то по теореме о трех перпендикулярах
Следовательно,
Так как то
Следовательно,
Тогда окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана правильная треугольная призма у которой сторона основания
а боковое ребро
Точка
— середина ребра
а на ребре
взята точка
так, что
а) Докажите, что плоскость делит отрезок
пополам.
б) Плоскость делит отрезок
на две части. Найдите длину
меньшей из них.
а) Так как то плоскость
пересечет грань
по
прямой
точка
— середина
Пусть
Требуется доказать, что точка
— середина отрезка
Так как — середина
то по теореме Фалеса
— середина
Что и требовалось доказать.
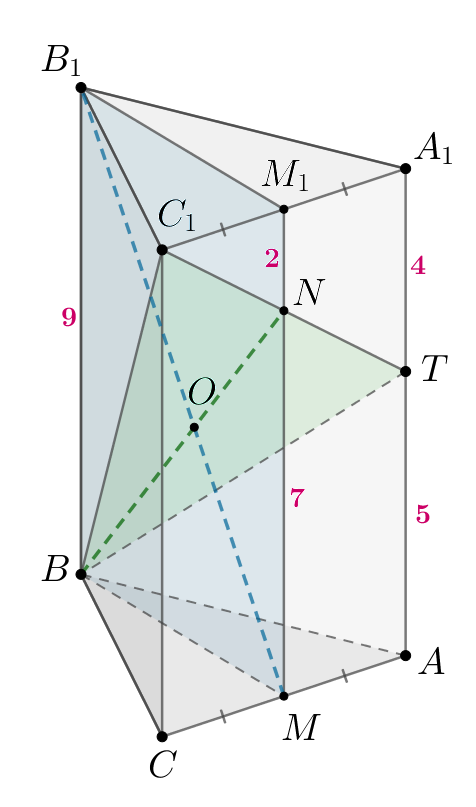
б) Прямая лежит в плоскости
Следовательно, плоскость
пересечет прямую
в той точке, в которой линия пересечения
плоскостей
и
пересекает прямую
Так как
то
Так как — средняя линия в
то
Значит,
Треугольники по двум углам:
как
вертикальные,
как накрест лежащие при
и
секущей
Следовательно,

Высота правильного треугольника
со стороной
равна
По теореме Пифагора из
Тогда с учетом равенства получаем
б)
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде известны длины ребер:
Точки
и
— середины ребер
и
соответственно. Плоскость
пересекает ребро
в точке
а) Докажите, что
б) Найдите площадь сечения параллелепипеда плоскостью
а) Назовем плоскость плоскостью
Так как плоскости
и
параллельны, то плоскость
пересечет их по параллельным прямым.
Следовательно, пусть
— середина
Тогда
Значит,
плоскость
пересечет грань
по отрезку
Так как
— середина
то по теореме Фалеса
— середина
то есть
Так как плоскости и
параллельны, то
пересечет их по
параллельным прямым. Проведем
Тогда
пересечет грань
по отрезку
Пусть Тогда
значит, так как
то
Так как
и
— середина
то по теореме Фалеса
— середина
Следовательно, так как
то
значит,
откуда
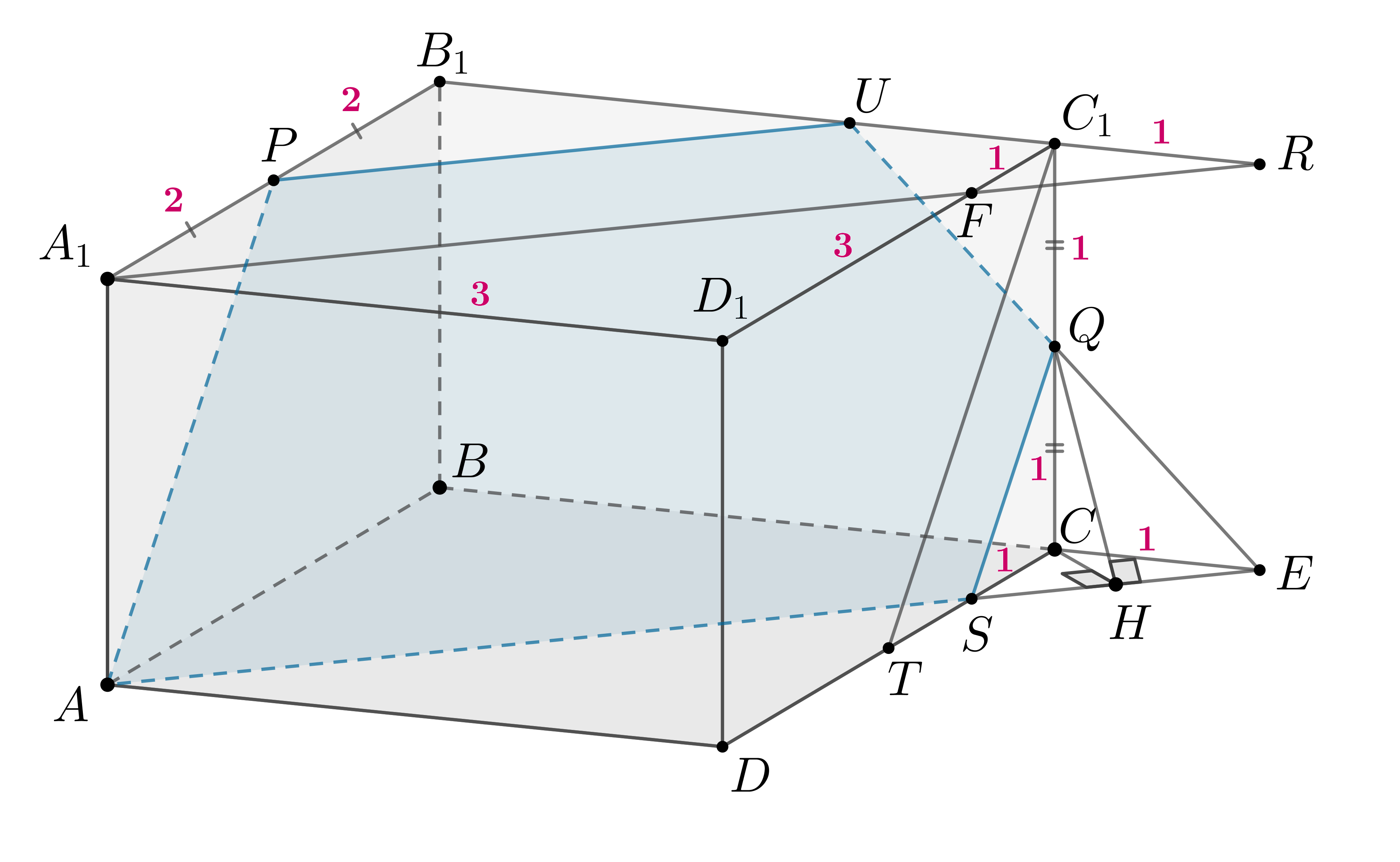
б) Пусть Так как
то
Тогда
— трапеция. Будем искать площадь сечения как
Заметим, что аналогично работе в верхней грани, Проведем
Тогда
— середина
По ТТП
Так как
—
средняя линия в
то
следовательно,
— высота
трапеции
Найдем
Тогда
Из равнобедренного прямоугольного имеем
Из
равнобедренного прямоугольного
имеем
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Основание шестиугольной пирамиды — правильный шестиугольник
Точки
и
— середины ребер
и
соответственно.
а) Постройте сечение пирамиды плоскостью, проходящей через точки
и
б) В каком отношении плоскость сечения делит отрезок, соединяющий вершину
с центром основания пирамиды, считая от вершины
а) Назовем плоскость плоскостью
Пусть
Рассмотрим
. Пусть
Тогда
— прямая, по которой
пересекает плоскость
Пусть
Тогда
— одна из
вершин сечения, лежащая на отрезке
Заметим, что так как
то
Так как
по свойству правильного шестиугольника, то плоскость
пересекает
плоскость
по прямой
, параллельной
Пусть
Тогда прямая
проходит через точку
следовательно,
проведем
через точку
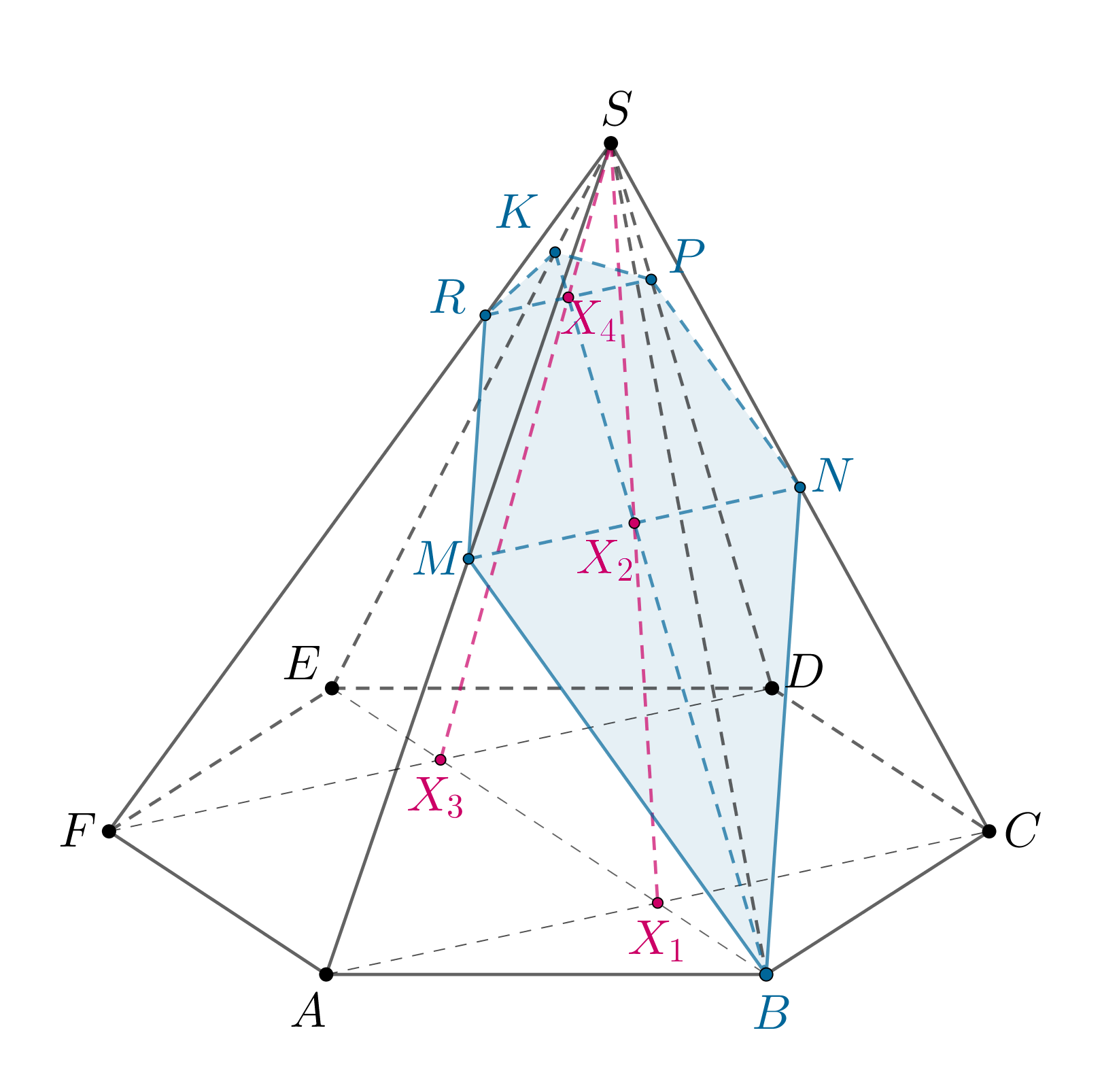
Тогда — сечение пирамиды плоскостью
Найдем положения вершин сечения.
Так как
— средняя линия
то
— середина
отрезка
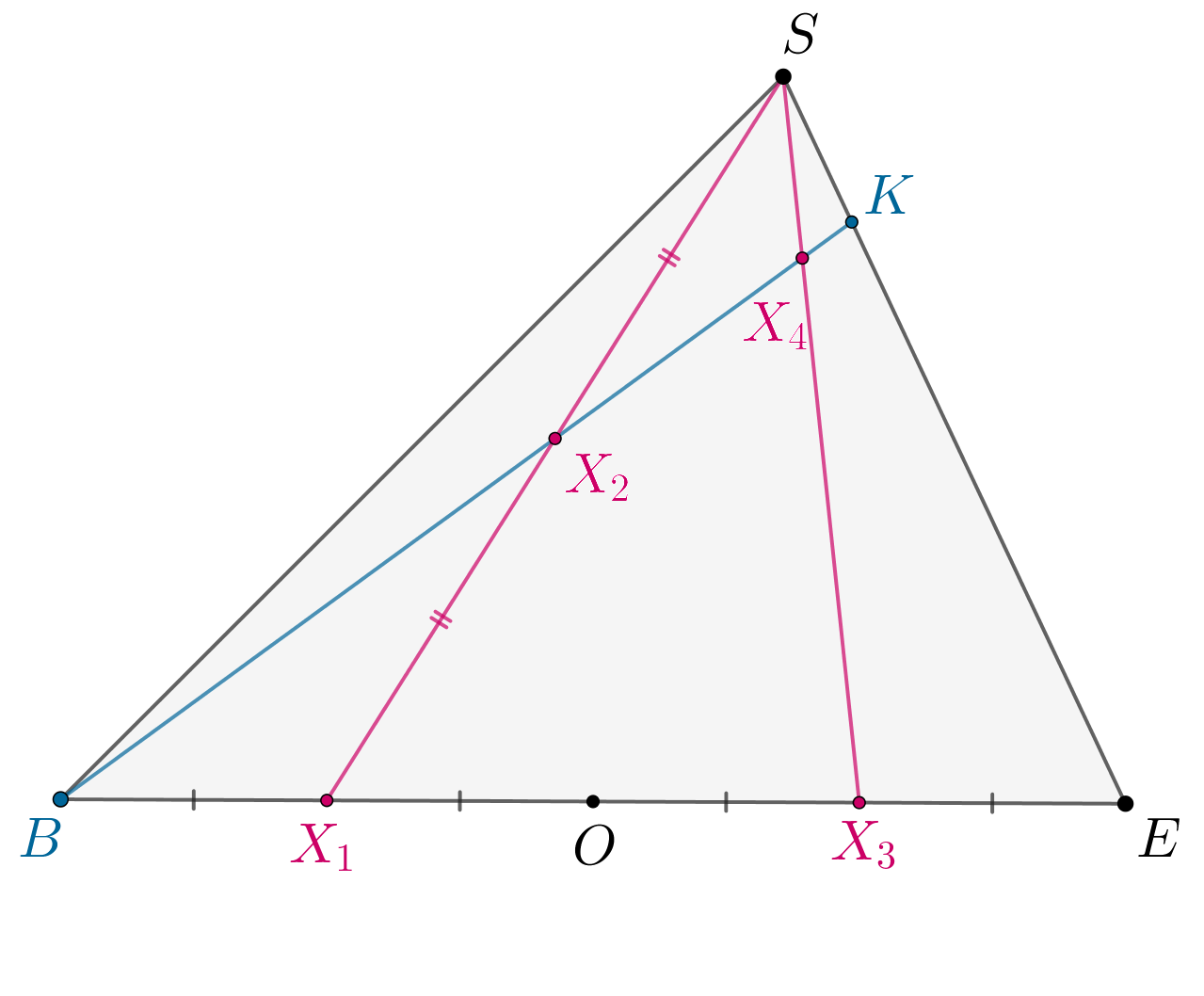
Пусть — центр шестиугольника
тогда
— середина
— середина
Следовательно, если
то
По теореме Менелая для и прямой
получаем
То есть делит отрезок
в отношении
считая от вершины
— середина отрезка
следовательно,
По теореме
Менелая для
и прямой
получаем
Так как
то
и
— точки, делящие в отношении
считая от вершины
отрезки
и
соответственно.
б) Рассмотрим Пусть
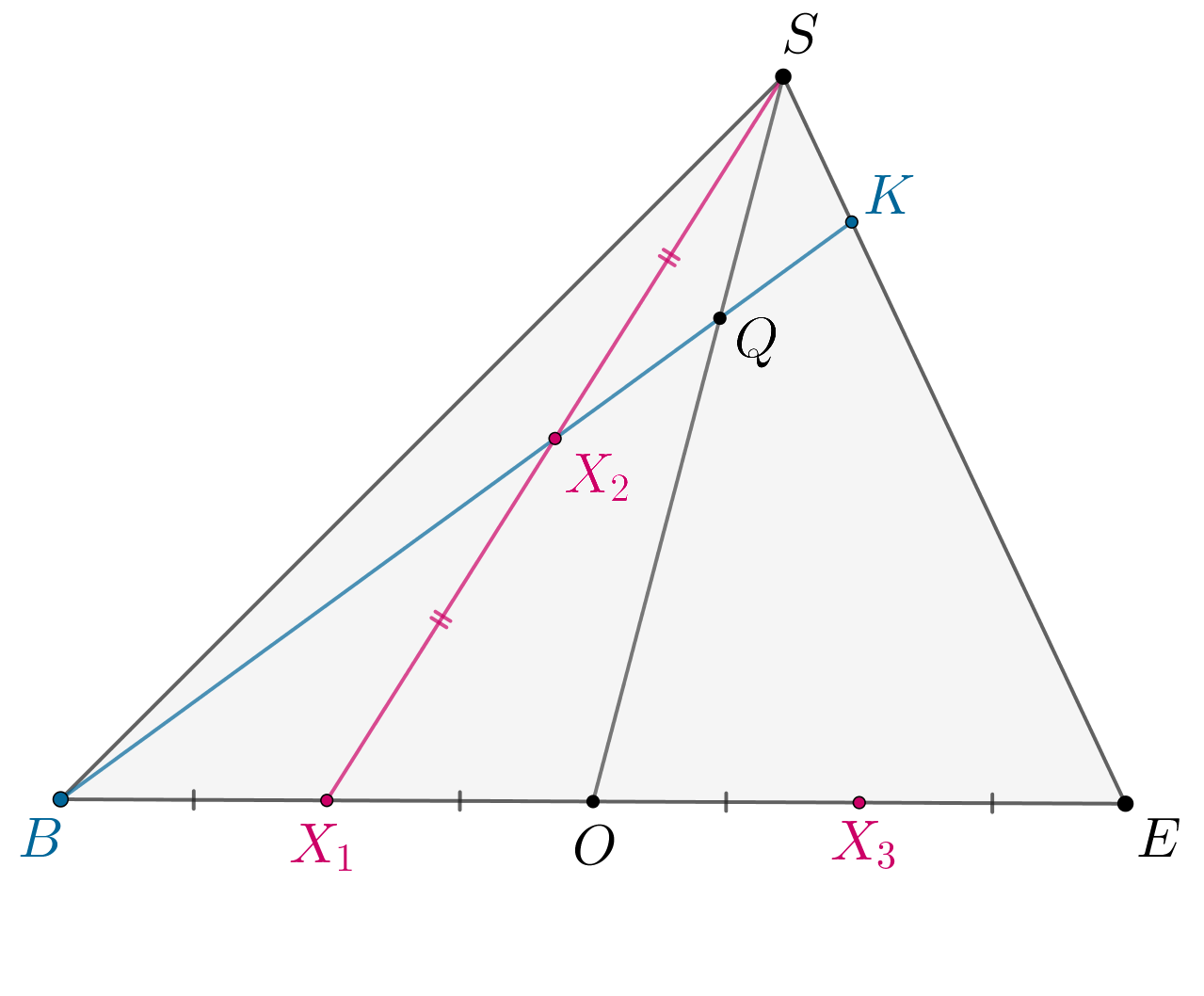
Запишем теорему Менелая для и прямой
Следовательно, плоскость делит отрезок
в отношении
считая от
вершины
б)



