Ошибка.
Попробуйте повторить позже
Диагонали и
равнобокой трапеции
пересекаются в точке
. Известно, что
:
. Окружность
с
центром
, проходящая через вершины
и
, пересекает продолжение основания
за точку
в точке
. Оказалось, что
. Найдите отношение основания
к радиусу окружности
.
Источники:
Подсказка 1
Давайте попробуем выразить каким-либо образом основание через радиус, чтобы в результате отношения радиусы сократились. Давайте проведем высоту из точки O на основание AD, тогда из прямоугольного треугольника мы можем найти, что AD = 2*AO*cos∠DAO. Таким образом, отношение AD к радиусу окружности будет равно 2cos∠DAO. Подумайте, откуда мы можем найти косинус данного угла?
Подсказка 2
Давайте обратим свое внимание на треугольник KBO, всё таки про него нам довольно много известно из условия. Он равнобедренный, а его сторона OK равна OA и OD. По условию нам дано отношение оснований нашей равнобокий трапеции. Подумайте, как, используя данное отношение, мы можем выразить KB и BO через сторону OK.
Подсказка 3
Если воспользоваться тем, что OK=OA=OD и тем, что △AOD подобен △BOC, можем найти, что BO=KB=2*OK/3. По сути, нам известны три стороны одного треугольника, выраженные через одну и ту же переменную, просто с разными коэффициентами. В таких случаях очень удобно использовать теорему косинусов. Давайте воспользуемся ей для угла KBO, так как ∠KBO = 180 - ∠OBC = 180 - ∠DAO. Таким образом, мы легко находим 2cos∠DAO.
Обозначим радиус окружности за ,
. Из
получаем
(с учётом условия
задачи).
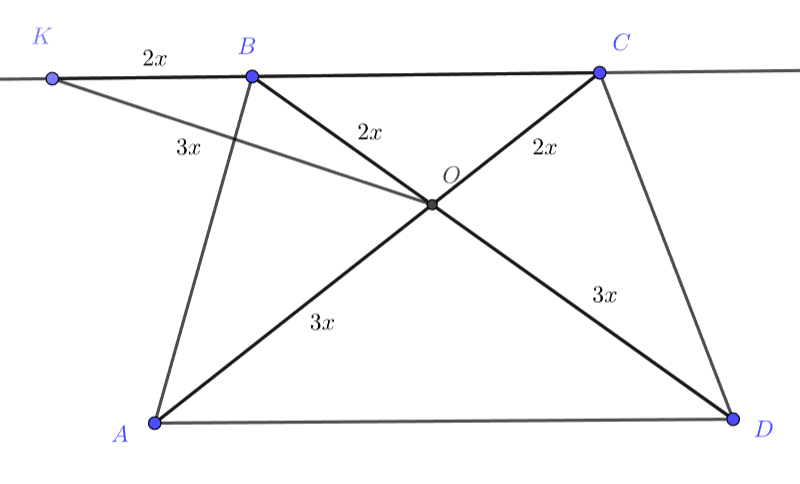
По теореме косинусов для
Если провести высоту треугольника , то легко понять, что
, отсюда
Ошибка.
Попробуйте повторить позже
Какое наибольшее количество параллелепипедов можно вырезать из кубика
?
Для начала покажем, как вырезать такое количество параллелепипедов. Очевидно, что с помощью таких параллелепипедов можно вырезать
часть кубика размера . Тогда останется часть размера
. Из неё, в свою очередь, можно вырезать кусок
—
останется часть размера
. И наконец, вырезав из этой части кусок размера
, оставим непорезанный кубик
.
Итого, мы вырезали
параллелепипеда.
Докажем теперь, что большее количество вырезать не получится. Действительно, разобъём кубик на “диагональные” слои (см.картинку
ниже), которые раскрасим по циклу в 4 цвета. Несложно убедится, что в каждом параллелепипеде содержится ровно 1 кубик
каждого цвета. При этом заметим, что при разбиении из примера у нас остался угловой куб размера
, в котором присутствуют
только кубики трёх цветов. Значит, существует цвет, в который покрашено ровно 52 кубика, поэтому не получится вырезать
параллелепипедов больше этого количества.

Ошибка.
Попробуйте повторить позже
Лёша выписал на доску числа ,
,
,
и так далее, без пробелов. После этого он стёр каждую вторую цифру написанную на доске (то
есть на доске осталось число
). Затем, в том что осталось, он стёр каждую третью цифру. Чему равна сумма цифр, стоящих
на
и
месте оставшегося числа?
Посчитаем на каких позициях останутся цифры после двух стираний. После первого стирания на доске останутся только цифры стоящие на
нечётные местах. После второго стирания мы вычеркнем цифры на ,
,
, …местах. Это числа, которые при делении на
дают
остаток
. Это действительно так, потому что если мы вычернкнули цифру на месте
, то останутся цифры на местах
,
, а следюущая —
-ая будет вычеркнута. Числа
и
дают одинаковые остатки при делении на
, а
значит, мы действительно вычеркнем все цифры ,позиции которых дают остаток
при делении на
, так как первое
вычеркнутое цифра будет
-ой. То есть оставшиеся цифры разбиваются на пары, в которых первая позиция даёт остаток
при
делении на
, а второая —
. А при делении на
их позиции дают остаток
. Это означает, что остались цифры стоящие
на местах, которые дают остаток
и
при делении на
. Если пронумеровать пары оставшихся цифр, то в паре с
номером
будут стоять цифры на местах вида
и
. Цифры стоящие на
-ом и
-ом месте
попадают в пару под номером
. Это значит, что там будут цифры
и
исходного
числа.
Теперь найдём что за цфиры там стоят. Числа от до
занимают
цифр, далее от
до
— ещё
цифр, всего
,
числа от
до
—
=
и всего
цифр. Числа от
до
дают нам
цифр, а значит в этом
промежутке стоит искать. Первая цифра встретится в числе
, причём так как
целое число,
то это будет последней цифрой в
. Вторая цифра, соотвественно, будет цифра
в числе
. В итоге получаем сумму
.
Ошибка.
Попробуйте повторить позже
Четырёхугольник вписан в окружность, причём
, а
. Известно, что
, а
.
—
центр окружности, в которую вписан четырёхугольник. Найдите
где
— площадь треугольника
.
Так как , то
и
— равнобокая трапеция. Заметим, что
, при этом
, а значит,
— равносторонний, и его площадь равна
. Найдём тогда длину
Опустим высоты и
на сторону
. Треугольники
и
— прямоугольные с углом
. Тогда
, а
. Заметим, что
— прямоугольник, причём
Таким образом, . Получаем, что площадь треугольника
равна
, а её квадрат —
![]()
Ошибка.
Попробуйте повторить позже
Данил хочет покрасить каждый из треугольников на диаграмме ниже в один из трёх цветов так, чтобы треугольники, имеющие общую сторону, были покрашены в разные цвета. Сколько способов это сделать у него есть?
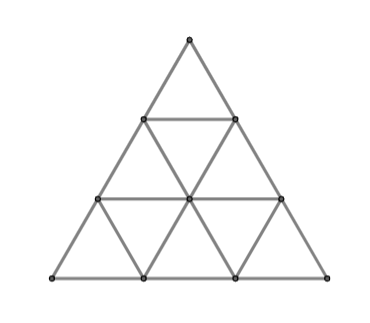
Давайте разобъём треугольники на три группы, которые будем последовательно красить (см. картинку ниже). Общее количество способов
покрасить треугольники из первой группы — При этом существует три типа их раскраски, которые мы далее рассмотрим по
отдельности: когда они все одинакового цвета, когда они все покрашены в разные цвета, и когда два треугольника покрашены в один цвет, а
оставшийся — в третий.
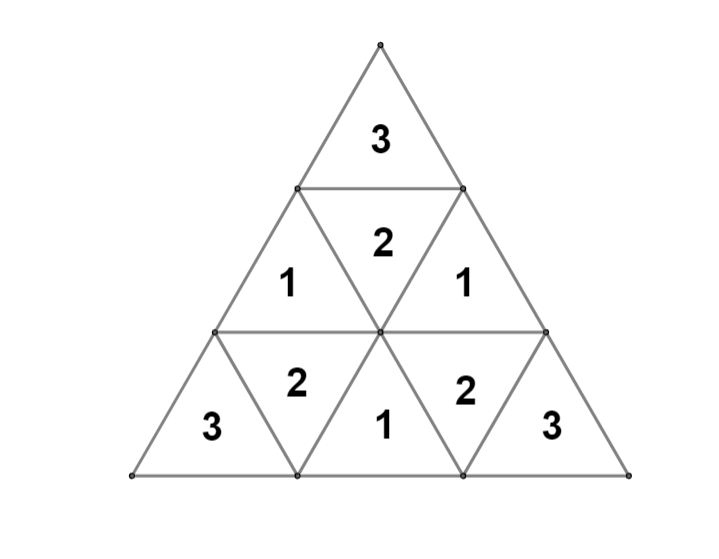
Вариант 1 (треугольники покрашены в один цвет): таких раскрасок ровно три штуки — по одной на каждый цвет. При этом, любой
треугольник из второй группы можно покрасить одним из двух способов — ведь оба его соседа покрашены в один и тот же цвет. Итого,
способов покрасить треугольники второй группы: . Аналогично, угловые треугольники из третьей группы тоже можно покрасить
8 способами. Итого, раскрасок первого типа:
.
Вариант 2 (треугольники покрашены в разные цвета): таких раскрасок шесть штук — вначале нужно выбрать цвет для верхнего
треугольника, потом покрасить правый в один из двух оставшихся цветов, и последний треугольник докрасить в оставшийся цвет. Цвет
каждого треугольника из второй группы восстанавливается однозначно — ведь у них два соседа разных цветов. Раскрасить же угловые
треугольники снова можно 8 способами. Итого, раскрасок второго типа: .
Вариант 3 (два треугольника одного цвета, и третий — другого): это все оставшиеся способы покрасить треугольники из первой группы, а
значит, их количество . Теперь у одного треугольника второй группы два одноцветных соседа, а у двух других — два
разноцветных соседа. Значит, их можно покрасить
способами. С угловыми же треугольниками всё также, как в предыдущих
случаях — 8 способов раскраски. Итого, раскрасок третьего типа:
.
Наконец, осталось сложить эти три количества и получить ответ: .
Ошибка.
Попробуйте повторить позже
Известно, что для положительных чисел и
выполняются равенства:
и
. Чему равно
?
Равенства из условия переписываются в виде и
. Если их сложить, то мы получим, что
. Отсюда следует, что
. В силу того, что числа положительны, то
. Из равенств выше,
следует, что
, а
. Далее подстановкой получаем, что
.
Ошибка.
Попробуйте повторить позже
У Ани есть шестерка и 7 девяток. Раз в минуту она может перевернуть какие-нибудь две цифры. Может ли у нее оказаться поровну шестерок и девяток? В ответ укажите “да” или “нет”.
Подсказка 1
Опять же, как и в одной из предыдущих задача - здесь выгодно рассмотреть что-то, что не меняется при наших операциях. Подумайте, что это может быть.
Подсказка 2
Какие здесь вообще есть параметры? Сумма? Может быть. Произведение? Точно не не подходит. Сумма кол - ва 6
Подсказка 3
Верно, на число 4, так как если мы увеличиваем или уменьшаем на 4, то остаток не меняется, ровно как и если мы прибавляем 0. Тогда, выходит, что разность кол - ва 6 и 9 имеет константный остаток при делении на 4. Осталось посмотреть на остаток начального набора и того, который просят получить в задаче!
Посмотрим на разность между количеством шестёрок и девяток. После любой из операций она может либо измениться на в любую
сторону, либо же не измениться совсем. Но это означает, что она не меняет свой остаток от деления на
. Изначально он был равен
, а должен стать равным
— противоречие.
Ошибка.
Попробуйте повторить позже
В королевстве живут графы, герцоги и маркизы. Однажды каждый граф сразился на дуэли с тремя герцогами и несколькими маркизами. Каждый герцог сразился на дуэли с двумя графами и шестью маркизами. Каждый маркиз сразился на дуэли с тремя герцогами и двумя графами. Известно, что все графы сразились с равным числом маркизов. Со сколькими маркизами сразился каждый граф?
Подсказка 1
Давайте начнём решать задачу с введения обозначений. То что нас просят найти, естественно обозначить за x, а графов, герцогов и маркизов за a, b и c соответственно. Нам по условию сказали на самом деле количество боёв с разных точек зрения. Какой способ решения задачи тогда здесь уместен? Как можно естественно посчитать бои?
Пусть каждый граф сразился с маркизами. Обозначим через
количество графов, через
— количество герцогов, через
—
количество маркизов. Заметим, что по условию всего боёв между герцогами и маркизами было с одной стороны
, а с другой —
,
откуда
. Аналогично посчитаем количество боёв между герцогами и графами двумя способами. Получим
. откуда
. Теперь осталось лишь посчитать количество боёв между графами и маркизами двумя способами. Получаем
, но тогда
, откуда
.
Ошибка.
Попробуйте повторить позже
Даны квадратные трёхчлены ,
и
. Оказалось, что любые два из них имеют общий корень, но все три
общего корня не имеют. Докажите, что выполнены ровно два неравенства из следующих трёх:
Подсказка 1
Давайте начнём с условия на то, что любые два из квадратных трёхчленов имеют общий корень, но все три общего корня не имеют. Что мы тогда можем сказать про кол-во корней каждого них? А сколько всего различных корней в совокупности этих трёх квадратных уравнений?
Подсказка 2
Да, у каждого из них по 2 различных корня, а у трёх вместе - 3. Давайте тогда обозначим их за x₁, x₂, x₃ и как-то распределим их между нашими уравнениями без ограничения общности и наконец-то воспользуемся теоремой Виета, чтобы заменить каждый из коэффициентов a, b, c на выражения с x₁, x₂, x₃.
Подсказка 3
После преобразований мы получим квадратные уравнения относительно какого-то из корней. Для примера, из первого неравенства получится: x₂² - (x₁+x₃)x₂ + x₁x₃ > 0, можем ли мы сразу сказать, какие корни у этого квадратного трёхчлена? А когда оно верно?
Подсказка 4
Да тут же снова теорема Виета, остаётся проделать такие же шаги для других неравенств, сделать правильный вывод и радоваться доказательству!
Понятно, что каждый трёхчлен имеет по два различных корня, пусть первый трёхчлен имеет корни и
, тогда со вторым он имеет
общий корень
, с третьим —
. Общий корень второго и третьего трёхчленов обозначим
. Выразим в первом неравенстве
коэффициенты через корни соответствующих трёхчленов по теореме Виета:
. После
тождественных преобразований получим
. Оно справедливо, когда
не лежит между
и
. Аналогично
для выполнения двух других неравенств необходимо, чтобы
не лежал между
и
,
не лежал между
и
. Но среди чисел
нет равных чисел, значит всегда какое-то одно находится между двумя другими, а два других — нет. Таким образом, выполнено
ровно два неравенства из трёх приведённых.
Ошибка.
Попробуйте повторить позже
У Маши в школе уроки заканчиваются в , мама встречает её на машине, и они едут домой. Однажды уроки закончились в
, и
Маша пошла домой пешком. По пути она встретила маму, которая, как обычно, поехала забирать дочь к
в школу. И дальше Маша с
мамой поехали домой на машине, причём приехали на
минут раньше обычного. Во сколько Маша встретила маму на дороге? (Скорости
Маши и мамы постоянны, время на посадку в машину не тратится.)
Ответ вносите в формате “ЧЧ:ММ”.
Подсказка 1
Обозначим путь, который прошла Маша пешком за x и будем отталкиваться от этого. На сколько меньше в таком случае прошла мама, чем обычно?
Подсказка 2
На 2x! (почему?). А за какое время мама проезжала это расстояние?
Подсказка 3
За те самые 12 минут, которые сэкономили Маша и мама) Тогда мы знаем, за какое время она бы проехала расстояние, которое прошла Маша! Осталось осознать, что же мы на самом деле нашли)
Пусть Маша прошла пешком расстояние . Тогда мама и по дороге к школе, и по дороге обратно проехала на
меньше, чем
обычно. Значит, мама проезжает расстояние
за
минут. Тогда расстояние
она проезжает за
минут. Отсюда
следует, что мама встретила Машу за
минут до того, как обычно приезжает в школу. Значит, их встреча произошла в
.
Ошибка.
Попробуйте повторить позже
Параболы и
пересекают ось
в точке
. Докажите, что если точки их вторичного пересечения с
осью
расположены симметрично относительно начала координат, то и точки их пересечения с осью
расположены симметрично
относительно начала координат.
Пусть первая парабола вторично пересекает ось в точке
, а вторая — в точке
. Тогда по теореме Виета
,
,
то есть
. Но эти параболы пересекают ось
в точках
и
, откуда и следует требуемое.
Ошибка.
Попробуйте повторить позже
Внутри шляпы волшебника живут кроликов: белые, синие и зелёные. Известно, что если произвольным образом вытащить из шляпы
кролика, то среди них обязательно найдутся три разноцветных. Какое наименьшее количество кроликов нужно достать из шляпы,
чтобы среди них точно было два разноцветных?
Источники:
Подсказка 1
Перефразируем условие: кроликов любых двух цветов вместе не более 80 (почему?)
Подсказка 2
Попробуем найти количество кроликов того цвета, которого больше всех. Для этого обозначим его за a (пусть они красные) и посчитаем, сколько красных и синих кроликов может быть в сумме?
Подсказка 3
Если синие это те, которые идут по своему количеству на втором месте, то в сумме их с красными не менее a + (100-a)/2 (почему?). Какой вывод можно сделать с учетом первой подсказки?
Подсказка 4
a + (100-a)/2 <= 80, значит a <= 60. А теперь вспомним, что a - это наибольшее количество кроликов одного цвета и сделаем из этого выводы)
Пусть в шляпе живёт белых кроликов и их больше всего. Пусть синие кролики вторые по количеству живущие в шляпе. Тогда их хотя
бы
. Из условия следует, что общее количество белых и синих кроликов должно быть не больше
(иначе можно
вытащить
кролика, среди которых не найдётся трёх разноцветных) и верно неравенство
. Отсюда
находим, что
. В силу того, что
— это наибольшее количество кроликов одного цвета, это означает, что если
произвольным образом вытащить
кролика из шляпы, то среди них точно найдутся два разноцветных. Заметим, что если
вытащить
кроликов, то этого может не хватить, например, если в шляпе живут
белых и по
синих и зелёных
кроликов.
Ошибка.
Попробуйте повторить позже
Можно ли так раскрасить все натуральные числа в красный и синий цвета, чтобы любые два числа, отличающиеся на 5, были разных цветов, и любые два числа, отличающиеся в два раза, были разных цветов? В ответ укажите “да” или “нет”.
Подсказка 1
Ну просто беее, а не задача. Раскрасить, да еще и все(!) натуральные числа. Да уж… Это ведь какой-то общий алгоритм надо придумывать, а потом еще и доказывать, что все числа будут использованы при таком алгоритме раскраски. Мда, ну и задача. Но это если думать, что ответ - «ДА», а вот если он противоположный, то можно, основываясь на условии задачи, найти контрпример и «дело в шляпе». Попробуйте это сделать!
Подсказка 2
Видимо нам нужно получить контрпример с тем, что число n будет и красным и синим одновременно, в условии того, что что - то известно про числа, которые связаны с данным(а именно отличаются от него на 5 или в два раза). Ну пусть числа n/2 и n-5. А вот если бы эти числа отличались на 5, то мы бы пришли к противоречию. А такое может быть?
Подсказка 3
Ну конечно, может. К примеру, если n=20. Тогда, с одной стороны, 20 имеет не совпадающий с 10 цвет, а с другой - не совпадающий с 15. Но при этом - 15 и 10 сами разных цветов, потому цвет 20 не совпадает с обоими цветами, которые у нас есть. Пришли к противоречию!
Рассмотрим числа и
. Они должны быть разных цветов. Посмотрим теперь на число
. С одной стороны оно должно быть цвета,
отличного от цвета
, а с другой — не такого же цвета как и
. Но такого быть не может так как цветов всего два —
противоречие.
Ошибка.
Попробуйте повторить позже
Над девятизначным числом разрешается производить следующее действие: любую цифру числа можно заменить на последнюю цифру
суммы цифр этого числа. Можно ли с помощью таких действий из числа получить число
? В ответ укажите “да” или
“нет”.
Подсказка 1
В таких задачах бывает очень полезно заметить что-то, что не меняется при наших операциях, так называемый инвариант. Потому как, если бы у начального числа это что-то было бы одним, а у конечного числа - другим, то мы бы сказали, что это невозможно. Попробуйте поделать операции, которые описаны в задаче и посмотреть на число, которое получается после замены. Может быть в нем что-то постоянно?
Подсказка 2
Ну вот , допустим , мы первый раз проделаем эту операцию. Цифра на которую надо будет заменять - это последняя цифра числа 35. То есть 5 - нечетная. Значит, все цифры нашего числа останутся нечетными. Но ведь проделав эту же операцию еще раз, мы опять получим нечетную цифру и, значит, опять число будет состоять только из нечетных цифр. Значит, мы нашли наш инвариант! А что теперь это нам дает? Правда, что мы решили задачу?
Заметим, что сумма цифр исходного числа нечётна. Тогда после замены оно всё ещё будет состоять только из нечётных
цифр и снова сумма цифр будет нечётна. Это означает, что число мы не получим, так как в нём есть чётные
цифры.
Ошибка.
Попробуйте повторить позже
В выпуклом четырехугольнике на сторонах
и
расположены точки
и
соответственно. Известно, что
,
и
Докажите, что
Подсказка 1
Множество параллельных прямых намекает нам, во-первых, на множество пар равных углов, но они нам в доказательстве мало чем могут помочь, а, во-вторых, на теорему о пропорциональных отрезках. Но если мы просто построим четырехугольник и проведем все прямые, то по такому рисунку мы не сможем применить никак теорему о пропорциональных отрезках. Подумайте, какое дополнительное построение нам необходимо для этого провести.
Подсказка 2
Давайте продлим прямые BA и CD до пересечения в точке T. Теперь мы можем записать две пропорции: AT/AP=(TD+DQ)/QC и TD/DQ=(TA+AP)/PB. Подумайте, как можно переписать то, что AB ⊥ AD, если мы знаем, что AB ⊥ BC и как нам могут помочь в дальнейшем доказательстве ранее полученные пропорции?
Подсказка 3
Для доказательства того, что AB ⊥ AD, на будет достаточно доказать, что AD параллельно ВC. Если мы перемножим пропорции крест накрест и вычтем одно выражение из второго, то получим равенство AT*DQ + AT*QC = AP*TD + BP*TD. Подумайте, почему это доказывает параллельность AD и BC.
Поскольку , то достаточно доказать
. Пусть
. Введём обозначения
.
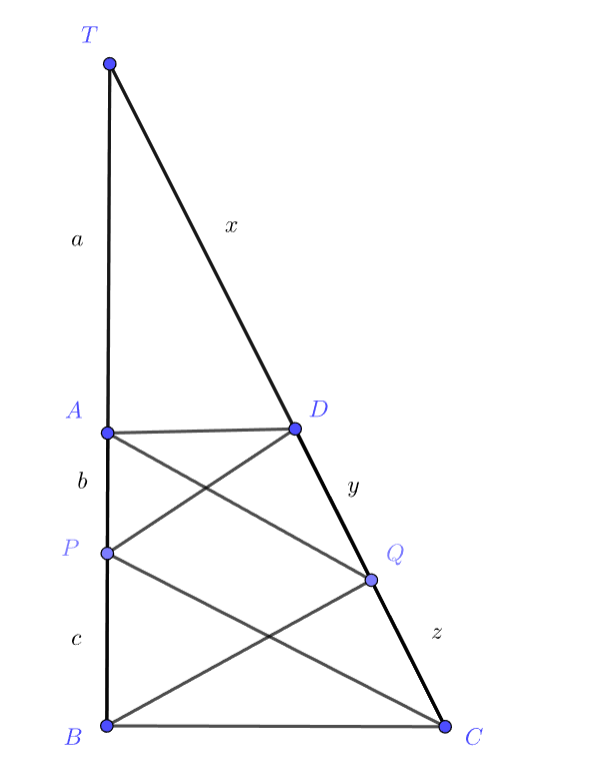
Из следует
Аналогично из
Нам же требуется показать
Остаётся заметить, что это равенство является разностью двух равенств выше.
Ошибка.
Попробуйте повторить позже
Числа от до
написаны на карточках. Можно ли разложить эти карточки в
мешков (чтобы в каждый мешок попала хотя бы одна
карточка) так, чтобы в каждом мешке произведение чисел на карточках делилось на
?
В ответ внесите “да” или “нет”.
Подсказка 1
Давайте, прочитав условие, поймём, а когда вообще произведение чисел в мешке будет делиться на 9? Какие возможны варианты?
Подсказка 2
Верно, нужно, чтобы в мешке либо было число делящееся на 9, либо два числа делящиеся на 3. Но таких чисел от 1 до 50 явно не много. Попробуйте посчитать, сколько их.
Подсказка 3
Ага, у нас получается пять чисел, кратных 9, и 11 чисел, кратных 3, но не кратных 9. Но получится ли тогда у нас раскидать их по мешкам, чтобы соблюдалось условие? Проверьте это, и задача решена!
Чтобы произведение чисел на карточках делилось на , то в мешке либо должна быть хотя бы одна карточка, число на которой делится на
, либо хотя бы две карточки, числа на которых делятся на
, но не делятся на
. Среди чисел от
до
есть
пять чисел кратных
—
,
,
,
и
. Их хватит на не более чем пять мешков. Чисел от
до
, которые
кратны
, но не кратны
, всего
—
,
,
,
,
,
,
,
,
,
,
. Этих чисел также хватит
не более чем на пять мешков. Получается, что максимум в десяти мешках произведение чисел может делиться на
—
противоречие.
Ошибка.
Попробуйте повторить позже
Точка – центр квадрата
. Найдите какие-нибудь семь попарно неравных векторов с концами и началами в точках
,
сумма которых равна нулевому вектору.
Подсказка 1
Попробуем облегчить себе работу и составить «цепочку» векторов с вершинами уже в данных нам точках.
Например,
Ошибка.
Попробуйте повторить позже
Лёша не поленился вычислить сумму
и выписать ее на доску. Сколько раз в итоговом результате записана цифра ?
Каждое слагаемое имеет вид . Тогда вся сумма имеет вид:
. Последними
цифрами этого числа будут
, а оставшиеся будут единицами. Так как мы испортили первые пять знаков, то остальные
будут единицами.
Ошибка.
Попробуйте повторить позже
В трёхзначном числе первую цифру (разряд сотен) увеличили на , вторую — на
, третью — на
. В итоге число увеличилось в
раза. Приведите пример такого исходного числа.
Подсказка 1
Пускай a, b, c- цифры числа x. Как х выражается через них?
Подсказка 2
x=100a+10b+c. Как изменится число x, если a увеличить на 3, b на 2 и с на 1?
Подсказка 3
100(a+3)+10(b+2)+(c+1)=100a+10b+c+321=x+321. По условию это число равняется 4x. Осталось только решить уравнение x+321=4x и убедиться, что x- натуральное трехзначное число.
Покажем, как можно найти ответ. Обозначим искомое число за . Тогда условие задачи можно записать как
и единственным
решением этого уравения будет
.
Ошибка.
Попробуйте повторить позже
Внутри треугольника , в котором
, взята точка
так, что треугольник
— равносторонний. Найдите
углы
и
Источники:
Подсказка 1
Нам явно не просто так дали два угла треугольника, давайте найдем и третий. Теперь подумайте как связаны углы BAC и BMC.
Подсказка 2
∠BAC = 2*∠BMC, кроме того они опираются на одну сторону BC. Если мы проведем окружность, описанную около треугольника ABC, то что мы можем сказать про точку M?
Подсказка 3
Точка M - центр описанной окружности около треугольника ABC, это значит, что AM=BM=СM. Зная это, найдите MAB и MAC
Опишем окружность около , тогда для её центра
выполнено
, при этом
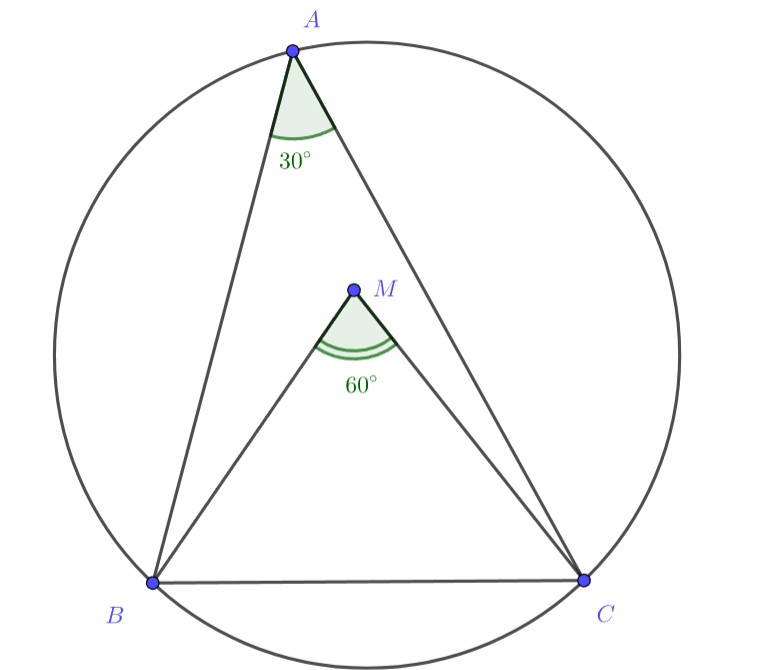
Получается, что является центром описанной окружности.
Далее легко посчитать



