Ошибка.
Попробуйте повторить позже
Произведение положительных чисел и
равно 1. Известно, что
Найдите .
Подсказка 1
Нам нужно как-то применить то, что ab = 1, заметим, что если раскрыть скобки, то будет сколько-то слагаемых с ab, может стоит попробовать так сделать?
Подсказка 2
Наступил коварный момент, все ab пропали и осталось только a² + b² = 47. Давайте попробуем вспомнить, где встречались сумма квадратов и ab?
Подсказка 3
Правильно в формуле квадрата суммы! Но нам не хватает слева 2ab, не забывайте, что мы всегда можем что-то добавить и сразу же убавить, или, что то же самое, прибавить с двух сторон уравнения равные величины. То что мы на верном пути нам так же подсказывает, что слева и справа получился полный квадрат, обратите внимание, что числа a,b - положительные!
Раскроем скобки
Так как
Добавим к обеим частям равенства
И так как и
положительные, получаем ответ.
Ошибка.
Попробуйте повторить позже
В пяти корзинах лежат яблоки двух сортов так, что в каждой корзине есть яблоки только одного сорта. Известно, что в первой корзине находится 20 яблок, во второй — 30 , в третьей — 40 , в четвёртой — 60, в пятой — 90. После того, как содержимое одной из корзин полностью продали, яблок первого сорта стало в два раза больше, чем яблок второго сорта. Сколько яблок могло быть в проданной корзине? Если ответов несколько, укажите их все через пробел в порядке возрастания.
Подсказка 1
Если яблок одного сорта в два раза больше, чем другого, то оставшаяся сумма яблок x + 2x = 3x делится на 3. Осталось только понять, сколько яблок какого сорта должно быть по итогу и возможно ли это.
Подсказка 2
Изначально было 240 яблок, что тоже делится на 3. Поэтому в проданной корзине не могло быть яблок, чьё количество не делится на 3, так как разность двух чисел, делящихся на 3, тоже делится на 3!
Подсказка 3
Остались варианты: 30, 60, 90. Однако обязательно надо проверить, что оставшееся количество яблок первого или второго сорта мы сможем набрать, используя оставшиеся корзины, так как в каждой должны лежать яблоки только одного сорта
Подсказка 4
Именно по этой причине в проданной корзине 30 яблок быть не может, так как второго сорта останется (240-30)/3 = 70 штук, и мы не сможем их разложить в коризны на 20, 40, 60, 90. Осталось проверить варианты на 60 и 90 яблок и, если все хорошо, привести примеры
Конечно, можно для каждой корзины попробовать её убрать и посмотреть, можно ли оставшиеся разбить на две группы, подходящих под условие. Но можно сократить перебор:
Если яблок первого сорта стало в два раза больше яблок второго сорта, то общее количество оставшихся яблок должно делиться на .
Первоначальное количество яблок равно
штук. Так как
делится на
, то количество убранных
яблок тоже должно делиться на
. Поэтому варианты на
и
яблок не подходят. Если убрали
яблок, то яблок
второго сорта должно быть
штук. Но
штук нельзя набрать используя корзины на
и
яблок.
Осталось проверить, что ответы и
достигаются. Для этого надо предъявить примеры, как могли быть распределены яблоки по
группам (сортам), чтобы количество яблок в одной группе было в два раза больше, чем в другой. Действительно:
Ошибка.
Попробуйте повторить позже
В шеренге стоит человека, и одного из них зовут Артур. Каждый из стоящих в шеренге либо рыцарь, который всегда говорит правду,
либо лжец, который всегда лжёт. Каждый, кроме Артура, сказал: «Между мной и Артуром стоят ровно два лжеца». Сколько лжецов в этой
шеренге, если известно, что Артур — рыцарь?
Если возможны несколько ответов, вносите в ответ через пробел в порядке возрастания.
Подсказка 1
Давайте попробуем поработать с тем условием, что между человеком и Артуром ровно 2 лжеца. Для каких людей тогда это условие проще проверить. Не бойтесь пробовать решить задачу для маленького числа людей, например, 5.
Подсказка 2
Если смотреть на кого-то, кто далеко от Артура, то между ними слишком много людей, даже если бы мы знали кто есть кто, то считать долго. Так давайте рассмотрим его соседей, что мы можем про них сказать?
Подсказка 3
Хорошо, мы поняли, что соседи Артура обязательно лжецы. Можем ли мы повторить эти же рассуждения для ещё каких-то людей?
Подсказка 5
Хорошо всегда задавать себе вопрос при решении задач, а есть ли какие-то граничные (крайние) случаи, которые меняют решение или ответ? Заметили ли вы, как меняется ответ в зависимости от положения Артура?
Заметим, что соседи Артура точно являются лжецами. Также, те, кто стоит через одного человека от Артура также заведомо являются лжецами. Это значит, что человек, который находится от Артура на расстоянии два (в любую из сторон) — рыцарь, так между ним и Артуром точно стоят два лжеца. Заметим, что тогда и следующий после рыцаря человек тоже обязан быть рыцарем и так далее. Получается, что все люди, которые стоят на расстоянии не менее чем в два человека от Артура — рыцари. Получается, что всего лжецов может быть не более четырёх человек. Все эти варианты возможны: если Артур стоит последним в шеренге, то лжецов будет двое, если же препоследним, то трое, а иначе лжецов будет четыре.
Ошибка.
Попробуйте повторить позже
Разбирается дело Брауна, Джонса и Смита. Один из них совершил преступление. В ходе следствия каждый из них сделал по два заявления. Браун: «Я не делал этого. Джонс не делал этого». Смит: «Я не делал этого. Это сделал Браун.» Джонс: «Браун не делал этого. Это сделал Смит.» Потом оказалось, что один из них дважды сказал правду, другой — дважды солгал, третий — раз сказал правду, раз солгал. Кто совершил преступление?
Подсказка 1
Следует разобраться кто и сколько правдивых утверждений мог сказать, для этого можно рассмотреть несколько случаев.
Подсказка 2
Очень интересный случай : Браун отрицает совершение преступления им и Джонсом, мог ли он соврать?
Подсказка 3
Правильно! Браун не мог солгать дважды, иначе преступление совершили бы и Браун, и Джонс, что невозможно по условию задачи!
Подсказка 4
А если Браун не соврал совсем? Тогда Джонс тоже говорит только правду! А это противоречит условию задачи.
Подсказка 5
Единственный возможный случай - если Браун и лжет, и говорит правду, при разборе этого случая становится понятно, что Браун и есть преступник!
Предположим, что вор — Смит. Тогда Браун и Джонс оба сказали правду дважды. Противоречие. Предположим, что вор — Джонс. Тогда Браун и Смит один раз солгали и один раз сказали правду. Также получили противоречие. Если же вор — Браун, то тогда условие задачи выполняется. Других вариантов, очевидно, быть не может.
Браун
Ошибка.
Попробуйте повторить позже
Существует ли число с суммой цифр 2022, которое делится на 2022? В ответ внесите “да” или “нет”.
Подсказка 1
Признаков делимости на 2022 удобных нам нет, поэтому попробуем построить число какого-нибудь красивого вида, а сумму его цифр проверим потом. Обратите внимание: 9191 делится на 91!
Подсказка 2
Посмотрим число вида 202220222022...2022 и сделаем так, чтобы сумма его цифр была 2022.
Например, подойдёт число . Оно делится на
, а его сумма цифр равна
.
Ошибка.
Попробуйте повторить позже
Рыцарский турнир длится ровно дней. К концу четвертого дня сэр Ланселот не успел сразиться лишь с одной четвертью от общего числа
участников турнира. А сэр Тристан к этому времени сразился ровно с одной седьмой из тех рыцарей, с кем успел сразиться сэр Ланселот.
Какое минимальное количество рыцарей могло участвовать в турнире?
Подсказка 1
Обозначим количество участников турнира за x, как тогда записать условие?
Подсказка 2
Тогда сэр Ланселот сразился с 3x/4 участниками, а сэр Тристан с 3x/28. Какие-то дроби, а количество участников вроде целое...на что тогда должен делиться x и какой тогда он?)
Пусть в турнире участвовало рыцарей. Тогда к концу четвёртого дня сэр Ланселот сразился с
участниками, а сэр Тристан с
. Оба числа должны быть целыми, а значит,
должно делиться на
. То есть
.
Ошибка.
Попробуйте повторить позже
Лёша выписал на доску числа ,
,
,
и так далее, с пробелами. После этого он стёр каждое второе число написанное на доске (то
есть на доске осталось числа
,
,
,
,
,
,…). Затем он стёр каждое третье число. Чему равна сумма чисел, оставшихся стоять на
и
месте?
После первого стирания на доске останутся только нечётные числа. Посмотрим на второе. Мы вычеркнем числа ,
,
, …. Это числа,
которые при делении на
дают остаток
. Это действительно так, потому что если мы вычернкнули число
, то останутся числа
,
, а следующее —
будет вычеркнуто. Числа
и
дают одинаковые остатки при делении на
, а значит, мы
действительно вычеркнем все числа, дающие остаток
при делении на
, так как первое вычеркнутое число равно
. То есть оставшиеся
числа разбиваются на пары, в которых первое число даёт остаток
при делении на
, а второе —
. А при делении на
эти числа дают
остаток
. Это означает, что остались числа дающие остаток
и
при делении на
. Если пронумеровать пары оставшихся чисел, то в
паре с номером
будут стоять числа вида
и
. Числа стоящие на
-ом и
-ом месте
попадают в пару под номером
. Это значит, что там будут числа
и
. Их сумма равна
.
Ошибка.
Попробуйте повторить позже
В школьном турнире по футболу приняло участие команды. После того как каждая команда сыграла с каждой по одному разу, то
оказалось, что команда «Катрапс» занимает «чистое» второе место, единственная набрав
очка. Сколько очков набрали остальные
команды? За победу в футболе даётся
очка, за поражение —
, за ничью —
очко.
Укажите ответ через пробел.
Если команда набрала очка за
игры, то либо она выиграла одну игру и проиграла две, либо же сыграла три игры вничью. Первый
вариант невозможен, так как иначе было ещё две команды, которые набрали хотя бы по три очка (победив «Катрапс»), то есть «чистое»
второе место мы бы не заняли. Значит было сыграно три игры вничью. Среди оставшихся трёх команд только одна могла
побеждать, иначе бы опять хотя бы у двух команд было больше трёх очков. Более того, у команды на первом месте должно
быть хотя бы
очка, а значит одна победа у неё точно была. Итак, у команды на первом месте есть хотя бы
очка, у
«Катрапса» —
, у
-го и
-го места по одному очку и осталась одна игра между победетилем и третьим или четвёртым
место и игра между третьим и четвёртым местом. Игра между третьим и четвёртым местом не могла закончиться чьей-то
победой, поэтому там точно была ничья, то есть у последних мест есть хотя бы по
очка у каждой команды. Если же
победитель сыграет с кем-то из оставшихся в ничью, то появится команда, у которой будет
очка, что противоречит
условие. Значит, последняя игра закончилась победой текущего первого места. В итоге команды набрали
,
,
и
очка.
Ошибка.
Попробуйте повторить позже
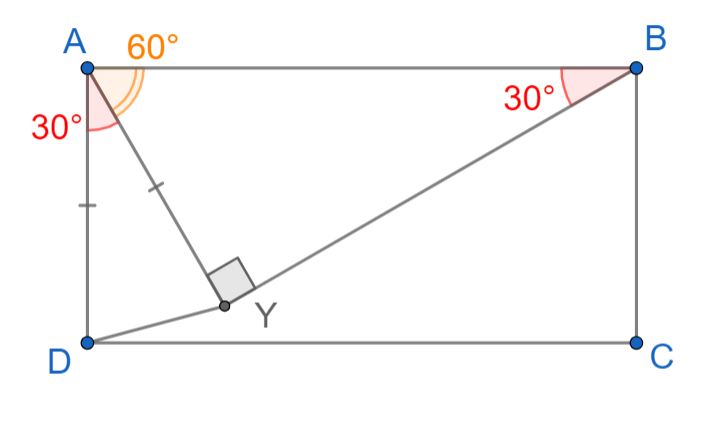
Внутри прямоугольника отмечена точка
такая, что
. Найдите угол
, если известно, что
.
Опустим на луч перпендикуляр из вершины
— полученную точку обозначим за
. Заметим, что треугольник
—
прямоугольный с углом
, а значит,
, а угол
. Тогда треугольник
— равнобедренный, и
. Получаем, что
. Но это означает, что точка
совпадает с точкой
из условия, и
.
Ошибка.
Попробуйте повторить позже
Дана операция , действующая по следующему правилу:
. Найдите сумму всех натуральных
, которые
удовлетворяют равенству
.
Распишем равенство :
Перебирая значения от 1 до 4 получаем, что подходит только 3. При
равенство не достигается, ведь
Ошибка.
Попробуйте повторить позже
Саша едет на электросамокате со скоростью равной целому числу километров в час. Известно, что она проезжает километров за целое
число часов. На следующей неделе вышло обновление в прошивке самоката и его скорость снизилась на
км/ч, но Саша всё ещё
проезжала
километров за целое число часов. Такая же ситуация продолжалось ещё две недели. С какой скоростью Саша ездила
изначально? Предполагается, что Саша всё время ездит с постоянной скоростью.
Пусть скорость Саши в начале месяца была равна . По условию
— целое число. Также, числа
,
и
тоже целые.
Перебирая всевозможные делители числа
получаем, что это может выполняться только для числа
.
Ошибка.
Попробуйте повторить позже
На доске написаны два натуральных числа, сумма которых равна . Если из одного числа стереть последнюю цифру, то получится
второе. Также известно, что одно из чисел делится на
. Чему равна разность этих чисел?
Раз одно из чисел делится на , то оно оканчивается на
. Оба числа не могут оканчиваться на
, иначе их сумма тоже будет
оканчиваться на
, а по условию это не так. Получается, что из числа, которое оканчивается на
стирают цифру и получают второе.
Таким образом наши числа имеют вид
и
. Тогда их сумма равна
, откуда
. Значит их разность равна
.
Ошибка.
Попробуйте повторить позже
На острове живут три племени аборигенов: рыцари, которые всегда говорят правду, лжецы, которые всегда лгут, и конформисты, которые могут лгать, только если их соседом является лжец (но могут сказать и правду). Перед путешественником стоят в ряд трое аборигенов. Он спросил каждого: «Ты конформист?». Все трое ответили «нет». Кто стоит перед ним?
Рыцарь на этот вопрос ответит «нет». Лжец ответит «да», поэтому лжецов перед нами нет. Конформист может дать ответ «нет» только если стоит рядом с лжецом. Но лжецов перед нами нет, поэтому конформист может отвечать только «да». Раз никто не сказал «да», то и конформистов перед нами нет. Значит, перед нами стоят три рыцаря.
Ошибка.
Попробуйте повторить позже
Сестры Галя и Валя празднуют день рождения в один и тот же день. Шесть лет назад, когда Валя была старше Гали в два раза, их кошка родила котёнка. Сейчас сумма возрастов девочек и котёнка равна 30. А сколько лет Гале сейчас?
Шесть лет назад сёстрам было суммарно лет. Валя была старше Гали в два раза, откуда следует, что Гале было 4 года, а
Вале 8. Значит, сейчас Гале 10 лет.
Ошибка.
Попробуйте повторить позже
Старшина выстроил рядовых в шеренгу. Затем он отправил каждого седьмого чистить картошку, каждого третьего из оставшихся — учить устав, а каждого пятого из оставшихся после этого — красить траву в зелёный цвет. После этого в строю остались 16 рядовых. Сколько их могло быть вначале? Если ответов несколько, указывайте через пробел.
Подсказка 1
Наверное, мы понимаем, что нужно решать такие задачи с конца. Давайте подумаем, что вообще происходит, когда каждый пятый человек уходит из строя. На сколько в долях уменьшается количество людей? Для лучшего понимания можно сначала рассмотреть меленькие примеры, а потом обобщить.
Подсказка 2
Верно, доля людей уменьшится на 1/5, если их число делилось на 5. А если не делилось, то последнего человека и не было, соответственно он никуда не уходил. Что это значит для нас? Какие варианты тогда возможны перед последним указания=ем старшины?
Подсказка 3
Ага, значит, общее число людей мы можем просто посчитать, зная, что их осталось 4/5. Получается их либо 20, либо 19(учитывая второй вариант). Теперь просто идя в обратном порядке, мы посчитаем возможные варианты количества людей в самом начале. Только не забудьте, что округление происходит вниз.
Пусть старшина отправил каждого -го из строя выполнять поручение. Тогда посмотрим на последнего ушедшего из него. Если он стоял
последнем в строю, то число людей делилось на
и после поручения их стало ровно на
меньше от всего строя. Но тоже самое
количество людей могло остаться, если бы последнего человека в строю не было. То есть мы получаем не более двух возможных исходов
того, сколько людей могло быть в строю до назначения работы.
После последнего поручения в строю осталось от всего отряда, кроме может быть одного человека. То есть людей могло быть
или же
(во втором случае из строя выйдут трое человек, кроме условного
-го, которого и так не было). После
предпоследнего, в строю осталось
от всего отряда, кроме может быть одного человека. В таком случае, если было
человек, то до
ухода их было
или
человек, а если
, то
, но так как число людей должно быть целым, то
их могло быть только
. После первого поручения в строю могло остаться
от всего отряда, кроме может одного.
То есть людей могло быть
или
, либо
, то есть
или же
, то есть
.
Ошибка.
Попробуйте повторить позже
Имеется гирек весом
,
, …,
грамм, из которых девять бронзовых, девять серебряных и одна золотая. Известно, что общий вес
бронзовых гирек на
грамм меньше, чем общий вес серебряных гирек. Найдите вес золотой гирьки.
Подсказка 1
Слишком мало данных для составления уравнений, не так ли? Надо искать другой путь...
Подсказка 2
Попробуем обозначить вес всех серебряных за х, тогда вес бронзовых = х-90, а еще одна золотая весом y. Их сумма = 190, отсюда следует лишь только четность веса золотой гирьки...
Подсказка 3
А если рассмотреть частичные суммы гирек? Это разумно, так как серебряные весят много больше бронзовых!
Подсказка 4
Идея минимальной суммы! Маленько поработай ручками и головой, и из нее однозначно следует вес золотой гирьки!
Девять самых легких гирек имеют массу грамм, а девять самых тяжелых —
грамм. Разность между весами этих двух наборов наибольшая из возможных и равна
граммов. Это означает,
что бронзовые гирьки самые лёгкие, а серебряные — самые тяжелые. Но тогда золотая гирька может весить только
граммов.
Ошибка.
Попробуйте повторить позже
Если записать все цифры даты января
года подряд, получится число
, которое читается одинаково слева направо и
справа налево. Такие числа называются палиндромами. А сколько всего дат-палиндромов будет в XXI веке (с
по
год)?
Подсказка 1
Лучше начать решать с года, его первая цифра задана однозначно, вторую цифру года следует обработать Вам.
Первая цифра года всегда будет равна , поэтому дата-палиндром должна иметь вид
. Далее посмотрим на третью и
пятую цифры. Они могут быть равны только
или
так как иначе номер месяца будет слишком большим. То есть даты
бывают только двух видов
и
. Дата второго вида может быть только одна
иначе
год будет не из XXI-го века. Но как видим, в такой дате будет «нулевое» число — противоречие. Значит, даты бывает
только первого вида:
. Второй месяц это февраль и в нём
дней. Любой из них даст одну возможную дату
палиндром, так как год будет лежать в нужных переделах. Осталось только проверить возможную дату с
февраля. Это
будет в
, что выпадает на високосный год, а поэтому такая дата корректна. Итого, получили
возможных
дат.
Ошибка.
Попробуйте повторить позже
На дороге через равные промежутки расположены пункты ,
,
,
,
и
. Вася хочет доставить посылку из пункта
в пункт
и вернуться обратно. Петя хочет доставить посылку из пункта
в пункт
и вернуться обратно. Они стартовали одновременно и в
первый раз встретились в пункте
. Скорости обоих постоянны. В каком пункте произойдёт их вторая встреча? Укажите латинскую
(английскую) букву.
Подсказка 1
Заметим, что скорости ребят постоянны, но не равны. Стартовали они одновременно, значит, до момента встречи они добрались за одно и то же время.
Подсказка 2
Как понять их скорости? Может быть, стоит посмотреть кол-во отрезков, которые они прошли.
Подсказка 3
К моменту встречи Петя прошел 3 отрезка, а Ваня - 2, тогда давайте считать, что скорость Пети - 3 отрезка в условную единицу времени, а скорость Вани - 2.
Подсказка 4
Через единицу времени Петя уже побывает в пункте А и пойдет обратно, остановившись в пункте В, а Ваня остановиться в пункте Е.
Подсказка 5
А еще через одну единицу времени Петя уже будет в пункте Е, а Ваня, побывав в пункте F, вернется в пункт Е, отсюда и следует, что они встретятся в пункте Е!
Предположим, что первая встреча произошла через час после выезда. Так как она случилась в пункте , то пока первый за час проезжает
два промежутка — между
и
и между
и
, второй проезжает три — между
и
,
и
, и
и
. Теперь расстояние
между ними равно десяти промежуткам, так как им надо проехать до противоположных пунктов, а затем развернуться и проехать
навстречу друг другу. Значит, что следующая встреча произойдёт через два часа и первый проедет четыре промежутка, остановившись в
пункте
.
Ошибка.
Попробуйте повторить позже
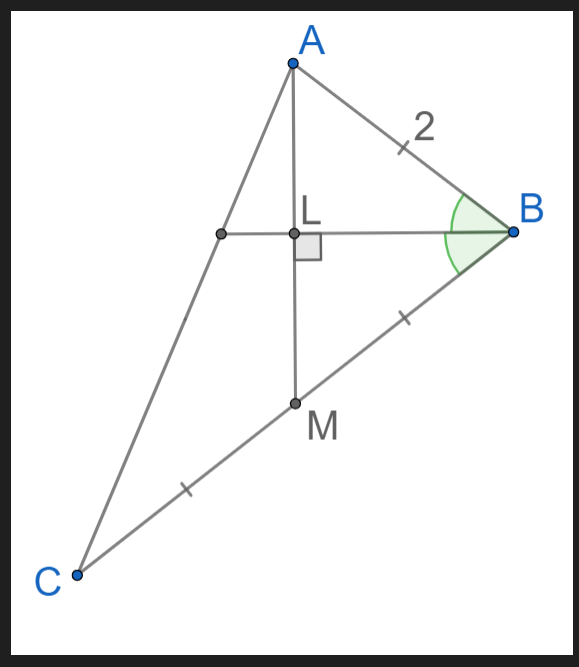
В треугольнике медиана, выходящая из вершины
, перпендикулярна биссектрисе угла
, а медиана, выходящая из вершины
,
перпендикулярна биссектрисе угла
. Известно, что
. Найдите периметр треугольника.
Подсказка 1
Так как два условия похожи друг на друга, то начнем разбираться только с одним из них. Обозначим медиану за AM , а её точку пересечения с биссектрисой за L. Что мы можем сказать про △AMB?
Подсказка 2
BL - одновременно биссектриса и высота, значит, △AMB - равнобедренный. Как теперь найти BC?
Подсказка 3
Так как M - середина BC, то BC = 2 * BM = 4. Для периметра осталось узнать AC. Как это можно сделать?
Обозначим медиану за , а её точку пересечения с биссектрисой за
. Тогда в треугольнике
отрезок
является
биссектрисой и высотой одновременно, а значит, треугольник
— равнобедренный. Откуда
, то есть
.
Аналогично,
, откуда получаем, что периметр треугольника равен
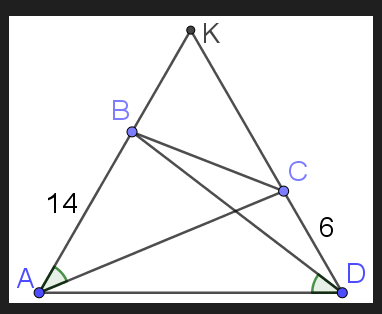
Ошибка.
Попробуйте повторить позже
Выпуклый четырёхугольник таков, что
и
. Найдите длину
, если известно, что
Подсказка 1
Два прилежащих угла четырёхугольника равны по 60 градусов. Какое удобное дополнительное построение можно сделать, чтобы получить эти углы уже в треугольнике?
Подсказка 2
Конечно, продлить AB и CD до пересечения в точке K и получить равносторонний треугольник. Поэтому можно искать не AD, а, например, KA или KD, так как они равны. Как теперь воспользоваться равенством углов ∠ BAC и ∠ BDA?
Подсказка 3
Докажите равенство треугольников △KCA и △BAD
Продлим стороны и
до пересечения в точке
. Заметим, что
, а значит, треугольник — равносторонний.
Тогда треугольники
и
равны по двум углам:
,
по условию; и прилежащей
стороне:
. Тогда
и сторона равностороннего треугольника равна
, а значит, и