Ошибка.
Попробуйте повторить позже
Две окружности и
пересекаются в точках
и
, общая касательная касается окружностей
и
в точках
и
соответственно (точка
лежит ближе к
, чем точка
). Луч
пересекает окружность
в точках
и
. Найдите
, если диагональ
четырехугольника
делит прямую
в отношении
считая от вершины
.
Источники:
Подсказка 1
Сразу попробуем воспользоваться условием и отметим равные углы. А чему равен угол ACD? Как воспользоваться тем, что CD - касательная?
Подсказка 2
Угол ADC равен AED, а угол ACD равен 180 - ABC. Что полезного можно вывести из этого? Как поближе подобраться к углам треугольника AED?
Подсказка 3
Угол ABE равен углу ACD (почему?). Как воспользоваться вписанностью? Нам было бы очень хорошо, если бы мы понимали, как воспользоваться тем, на какие отрезки AM делит AM...
Подсказка 4
Оказывается, треугольники AED и ADC подобны! Тогда что можно сказать интересного о прямой AM?
Подсказка 5
Это биссектриса угла AEC! Как воспользоваться найденным подобием? Вспоминаем свойство биссектрисы и находим требуемую дробь!
![]()
Отметим равные углы. по свойству угла между касательной и хордой. Градусная мера угла
вдвое меньше дуги
содержащую
окружности
по свойству угла между касательной и хордой. Тогда
так как градусная
мера дуги
не содержащую
равняется
Следовательно,
Также
как вписанные.
Из этого следует, что треугольники
и
подобны. Это значит, что
то есть
— биссектриса угла
Запишем соотношения из подобия
и
По теореме о биссектрисе получаем
Тогда получаем, что
Ошибка.
Попробуйте повторить позже
Диагонали и
трапеции
пересекаются в точке
а отношение оснований
Точки
и
— центры
окружностей
и
вписанных в треугольники
и
соответственно. Прямая, проходящая через точку
пересекает
в точках
и
а
— в точках
и
(
и
находятся ближе к
). Найдите радиус окружности
если
а
Источники:
Подсказка 1
Треугольники △AMD и △CMB подобны с коэффициентом 1/2, поэтому все соответствующие элементы относятся как 1/2. Нам дано произведение MZ*MY, которое напоминает произведение секущей на внешнюю часть. Но ведь мы знаем, что MZ/MX=1/2, поэтому легко находим MX*MY=10. А чему там равняется произведение секущей на внешнюю часть?
Подсказка 2
Конечно, квадрату отрезка касательной! Давайте отметим точку касания T: окружности ω₁ c отрезком BM. Тогда MT=√10. Если бы мы еще нашли MI₁, всё было бы в шоколаде...
Подсказка 3
Мы знаем, что MI₁/MI₂=2 и при этом MI₁+MI₂=13/2. Тогда MI₁=13/3. Воспользуйтесь теоремой Пифагора и завершите решение!
![]()
Пусть центр окружностей и
это
и
соответственно. Пусть точка
— точка касания
на
Тогда
| (1) |
Рассмотрим треугольники и
Они подобны с коэффициентом
Из этого следует, что
как
соответственные элементы в подобных треугольниках. Тогда
Используя , получаем
Пусть радиус это
тогда радиус
это
Тогда нужно найти
Рассмотрим
Из подобия и
получаем , что
из этого следует, что
Тогда
Ошибка.
Попробуйте повторить позже
Дан прямоугольный треугольник Окружность, касающаяся прямой
в точке
пересекает высоту
проведённую к
гипотенузе, в точке
а катет
— в точке
Известно, что
. Найдите отношение площади треугольника
к площади треугольника
Источники:
Подсказка 1
Пупупу… Точки E, F, B – лежат на одной окружности, причем точки E и F соединены! А что нам может помочь найти окружность? Правильно, равные углы. Что надо сделать, чтобы выйти на эти равные углы?
Подсказка 2
Да, нужно соединить все точки, лежащие на этой окружности, то есть надо соединить B с E и B с F! Тогда нетрудно видеть, что ∠CBF=∠FEB(угол между хордой и касательной), а также в силу параллельности ∠FEB=∠ABE! Таким образом, в силу равенства ∠CBF и ∠ABE: при гомотетии с некоторым положительным коэффициентом BF перейдет в BE, поскольку △ABC∼△CDB! Какие соотношения из этого можно написать?
Подсказка 3
Да, поскольку точки E и F разбивают отрезки AC и CD соответственно на два отрезка с одинаковым отношением(это первое соотношение), а также можно применить теорему Фалеса(это второе соотношение)! Какой вывод из этого можно сделать?
Подсказка 4
Верно, получается, что CF=DF! То есть, F – середина отрезка CD. Осталось заметить лишь одно подобие треугольников, какое же?
Подсказка 5
Верно, △ACD∼△ECF, потому что EF – средняя линия △ACD! Теперь нужно только расписать отношение площадей!
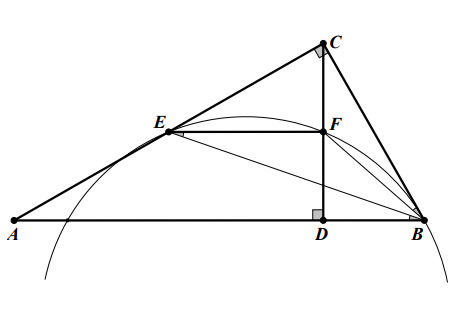
Соединим точку с точками
и
Так как
то
а
по теореме об угле между касательной и хордой. Поэтому
Следовательно,
и
— соответствующие элементы в подобных прямоугольных треугольниках
и
(По
двум углам:
— общий и
Значит,
По обобщённой теореме Фалеса
Из полученных равенств следует, что
Значит, — середина
а так как
то
— средняя линия
Отсюда
А значит,
Ошибка.
Попробуйте повторить позже
Окружности и
касаются в точке
внутренним образом. Отрезок
— диаметр большей окружности
а хорда
окружности
касается
в точке
Луч
повторно пересекает
в точке
Прямая, проходящая через точку
перпендикулярно
повторно пересекает
в точке
Найдите радиусы окружностей, угол
и площадь треугольника
если известно, что
Источники:
Подсказка 1
У нас на картинке есть пара касающихся окружностей. В такой ситуации бывает полезно отметить центры этих окружностей: пусть Q- центр w, а O- центр Ω. Что мы можем сказать про точки A, O, Q и B?
Подсказка 2
Верно, они лежат на одной прямой! Мы знаем, что ∠ACB=90° (AB- диаметр Ω) и ∠QDB=90° (BD- касательная к w). Тогда △BQD и △BAC- подобны. Что это нам дает?
Подсказка 3
Давайте обозначим за R- радиус Ω и r- радиус w. Тогда т.к. BQ/BA=BD/BC=13/18 ⇒ (2R-r)/2R=13/18 ⇒ r/R=5/9. Надо как-то посчитать радиусы. Давайте обозначим за K- вторую точку пересечения BA с w. Воспользуйтесь теоремой о касательной и секущей...
Подсказка 4
BD²=BK*BA=(2R-2r)*2R ⇒ R=39/8 и r=65/24. Теперь нам надо найти уголочек ∠FAE. Мы видим, что он равен половине суммы дуг AC и CE окружности Ω. Но половинка дуги AC равна уголочку ∠ABC, а его мы можем найти. Давайте тогда обозначим его за ψ. Чему равен уголок ∠QAD (сначала найдите ∠AQD)?
Подсказка 5
Т.к. ∠AQD- внешний для треугольника BQD, то ∠AQD=90°+ψ. Видно, что отрезки AQ и QD равны как радиусы ⇒ ∠QAD=45°-ψ/2 ⇒ дуга EB=2*∠QAD=90°-ψ. Дуга AB=180° и AB=AС+CE+BE ⇒ CE=90°-ψ ⇒ ∠AFE=(2ψ+90°-ψ)/2=45°+ψ/2. Что мы можем сказать про уголок ∠FAE?
Подсказка 6
Т.к. AC // FE ⇒ дуга AF равна дуге CE и равна 90°-ψ ⇒ дуга FE равна FA+AC+CE=90°-ψ+2ψ+90°-ψ=180° ⇒ ∠FAE=90°. Тогда в прямоугольном треугольнике △FAE мы знаем гипотенузу FE (FE=2R) и острый угол ∠AFE=45°+ψ/2 (ψ можно найти из прямоугольного треугольника △ABC). Я не сомневаюсь в том, что вам под силу довести решение до конца!
Обозначим , а радиусы
и
через
и
соответственно. Пусть
и
— центры окружностей
и
соответственно;
— точка пересечения
и
, отличная от
![]()
Отметим, что (касательная
перпендикулярна радиусу
) и
(угол вписан в окружность
и
опирается на её диаметр). Значит, треугольники
и
подобны (по двум углам). Отсюда
По теореме о касательной и секущей
Следовательно,
Далее находим углы и дуги:
Следовательно,
Угол
известен, так как
Значит,
Перейдём к нахождению площади. Треугольник прямоугольный
как вписанный угол, опирающийся на диаметр),
поэтому
Ошибка.
Попробуйте повторить позже
Остроугольный треугольник вписан в окружность
с центром О. Окружность, проходящая через точки
и
, пересекает
отрезок
в точке
. Касательные к
, проведённые через точки
и
, пересекаются в точке
. Отрезок
пересекает сторону
в точке
. Известно, что площади треугольников
и
равны соответственно
и
.
а) Найдите площадь треугольника .
б) Пусть дополнительно известно, что . Найдите
.
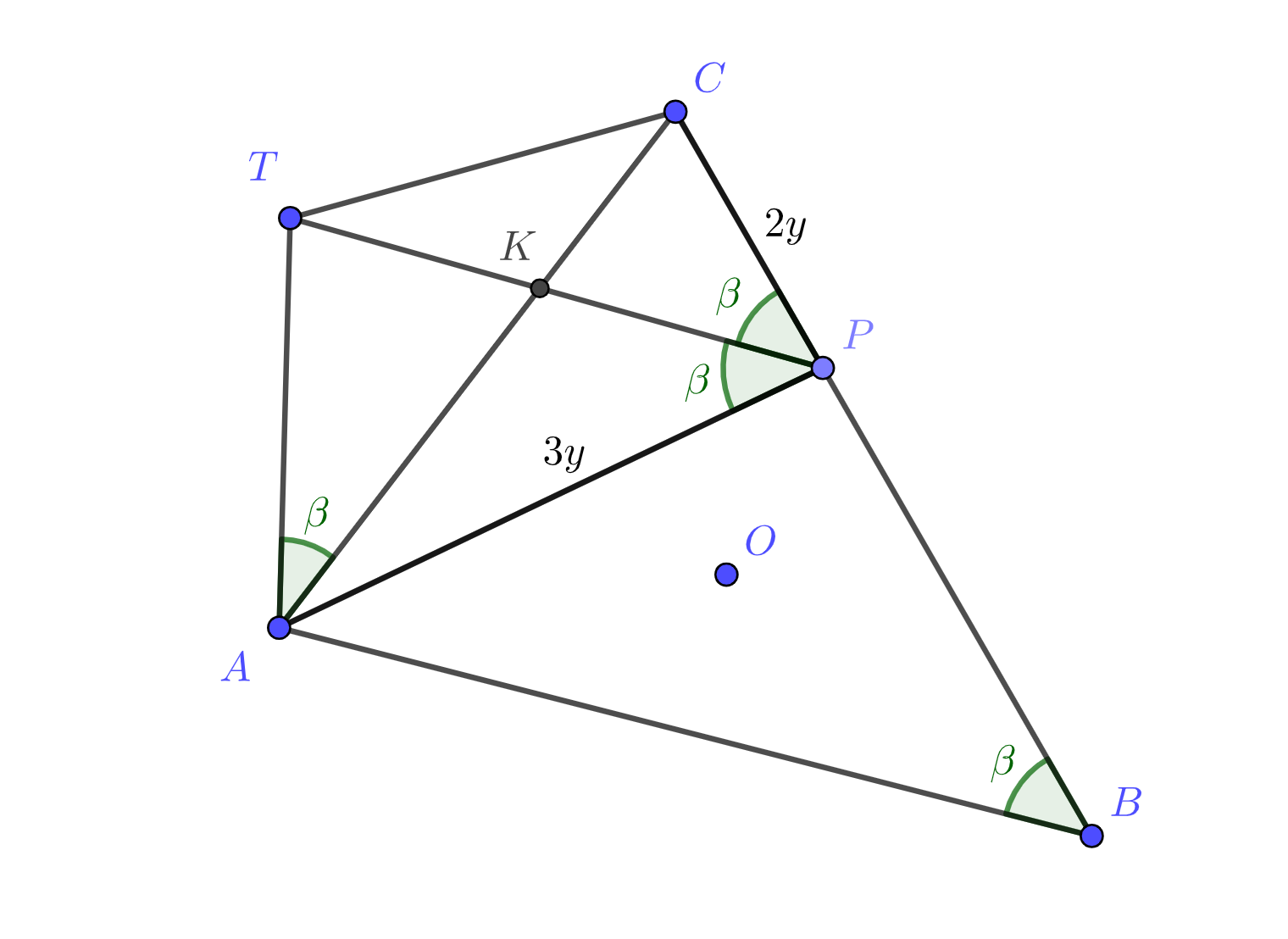
a) Так как прямые и
- касательные к
, они перпендикулярны радиусам, проведённым в точки касания, и
. Отсюда следует, что точки
и
лежат на окружности с диаметром
(назовём эту окружность
). На этой
же окружности лежит точка
, поскольку она лежит на окружности, проходящей через точки
. Обозначим
. Тогда по
свойству угла между хордой и касательной получаем, что
. Далее,
(углы, вписанные в окружность
).
Из того, что
, следует, что
.
Так как у треугольников и
общая высота, проведённая из вершины
, их площади относятся как основания, т.е.
. Треугольники
и
подобны, поскольку
, и коэффициент подобия
равен
. Но тогда
б) Поскольку острый, то
(центральный угол вдвое больше вписанного),
(вписанные в
углы, опирающиеся на одну дугу). Следовательно,
биссектриса треугольника
(также можно заметить, что
, как вписанные и как угол между касательной и хордой соответственно). Биссектриса треугольника делит
противоположную сторону пропорционально двум другим сторонам, поэтому
. Пусть
; тогда
Из дополнительного условия . Следовательно,
Площадь треугольника равна
, откуда получаем
,
. По теореме
косинусов из треугольника
находим, что
, откуда
окончательно получаем
.
Решён пункт а) – 4 балла;
частичные продвижения за пункт а):
доказано, что 𝑃𝐾 ‖ 𝐴𝐵 – 2 балла;
доказано, что четырёхугольник 𝐴𝑂𝐶𝑇 вписанный – 1 балл (не суммируется с вышеуказанными 2 баллами).
Решён пункт б) – 3 балла;
частичные продвижения за пункт б):
доказано, что 𝑃𝐾 – биссектриса треугольника 𝐴𝑃 𝐶 – 1 балл.
Ошибка.
Попробуйте повторить позже
а) Две параллельные прямые и
касаются окружности
с центром
в точках
и
соответственно. Окружность
с
центром
касается прямой
в точке
, пересекает прямую
в точках
и
, а также вторично пересекает
окружность
в точке
(при этом точка
лежит между прямыми
и
). Известно, что отношение площади
четырёхугольника
к площади треугольника
равно 2. Найдите отношение радиусов окружностей
и
б) Найдите эти радиусы, если дополнительно известно, что .
Источники:
![]()
а) Пусть - радиусы окружностей
,
соответственно,
, а прямые
и
пересекаются в точке
. Тогда из
условия касания
(
— диаметр) и
, откуда
, а
. Треугольники
и
равны по трем сторонам, поэтому
. Площадь треугольника
равна
. Применим данное в условии отношение площадей
и
. Кроме того, как расстояния между прямыми, равны
, откуда
, следовательно
, и
.
б) Из прямоугольного треугольника получаем
, то есть
. Итак,
и
.
Отсюда
.
а) ; б)
Ошибка.
Попробуйте повторить позже
Две окружности одинакового радиуса пересекаются в точках
и
. На первой окружности выбрана точка
, а
на второй - точка
. Оказалось, что точка
лежит на отрезке
, a
. На перпендикуляре к
,
проходящем через точку
, выбрана точка
так, что
(точки
и
расположены по разные стороны от прямой
.
а) Найдите длину отрезка .
б) Пусть дополнительно известно, что . Найдите площадь треугольника
.
Источники:
Подсказка 1
Самая естественная мысль, которая возникает это найти отрезок из теоремы Пифагора. Тогда нам нужно найти два катета. Подумаем, как удобнее всего выразить сторону в треугольнике, если мы знаем радиус описанной окружности?
Подсказка 2
Верно, их можно выразить через теорему синусов. Для этого нам осталось только обозначить удобный угол и найти стороны.
Подсказка 3
Теперь попробуем ввести ещё один угол бетта, равный углу BCF, и узнать углы треугольника АDС. Что можно сказать про тангенс угла бетта, как можно выразить его через отрезки?
Подсказка 4
Ага, понимаем, что тангенсы углов BCF и DAB равны, а значит и углы эти равны. Теперь осталось выразить сторону АС треугольника АCF и найти его площадь.
![]()
а) Пусть - радиусы данных в условии окружностей,
. Тогда
, и по теореме синусов для
:
для :
Значит,
откуда
б) Так как , то
. Далее, углы
и
вписаны в равные окружности и опираются на одну
и ту же хорду
, поэтому они равны, и из прямоугольного треугольника
находим, что
.
Тогда
поэтому
Итак,
, где Значит,
а)
б)
Ошибка.
Попробуйте повторить позже
Хорды и
окружности с центром
имеют длину 10. Продолжения отрезков
и
соответственно за точки
и
пересекаются в точке
, причем
Прямая
пересекает отрезок
в точке
Найдите отношение
Подсказка 1
Что мы можем сказать, про четырехугольник ABCD, если прямые, содержащие стороны AB и CD, пересекаются вне окружности, и AB=CD, и это хорды окружности?
Подсказка 2
Конечно, что это трапеция. А если это трапеция, то как мы обычно ищем отношение, в котором ее диагональ делит точка пресечения диагоналей? А что нам нужно, чтобы найти это отношение?
Подсказка 3
Верно, мы ищем это отношение через подобие треугольников BCL и ADL, и это отношение равно AD к BC. Знаем ли мы это отношение, если у нас дан отрезок CD и DP?
Так как , то
— равнобедренная трапеция.
Значит, . Отсюда треугольники
и
равны по трем сторонам и значит
— биссектриса
.
![]()
Тогда по свойству биссектрисы .
Ошибка.
Попробуйте повторить позже
Окружности и
касаются внешним образом в точке
, а их общая внешняя касательная касается окружностей
и
соответственно в точках
и
. Прямая
проходит через точку
, вторично пересекает окружность
в точке
, а также
пересекает
в точках
и
(точка
расположена между
и
. Общая касательная окружностей, проходящая через точку
,
пересекает прямые
и
в точках
и
соответственно (точка
лежит между точками
и
. Известно, что
.
а) Найдите длину отрезка .
б) Найдите радиусы обеих окружностей.
Подсказка 1
Понятно, что этот отрезок целиком сразу мы найти не сможем. Попробуем сделать это по частям: сначала найдём HF, потом PF. У нас есть множество секущих и касательных. Тогда какую теорему можно попробовать применить для нахождения отрезков касательных?
Подсказка 2
Верно, это теорема о касательной и секущей. Отсюда сразу находим HF и остальные отрезки секущей BE. Осталось вспомнить, что отрезки касательных из одной точки равны и найти PF.
Подсказка 3
Попробуем воспользоваться идеей, что нам известен отрезок АВ и конструкция из прямоугольной трапеции. Понятно, что неизвестные радиусы можно обозначить за R и r. Тогда какое естественное уравнение мы можем уже записать для них?
Подсказка 4
Ага, можно записать теорему Пифагора. Отсюда мы получили первое уравнение на радиусы. Теперь, так как катет и гипотенуза треугольника выражены через радиусы, хочется попробовать найти значение косинуса этого угла. Попробуйте найти равенство углов, а затем вспомнить, какая теорема в треугольнике лучше всего ищет угол?
![]()
а) Трижды применяем теорему о касательной и секущей:
Поскольку отрезки касательных, проведённых к окружности из одной точки, равны между собой, , следовательно,
. Итак,
.
б) Пусть . Тогда по теореме косинусов для треугольника
получаем
, т.е.
, откуда
,
Пусть
и
— центры, а
и
— радиусы окружностей
и
соответственно; так как окружности касаются, точка касания
лежит на линии центров
, и при этом
. Углы
и
четырёхугольника
прямые, поэтому
.
Рассмотрим прямоугольную трапецию . В ней
. Опуская из точки
высоту
на основание
, получаем прямоугольный треугольник
, в котором
. По теореме
Пифагора получаем
Кроме того,
Находим, что
а)
б)
Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике проведена диагональ
и в каждый из полученных треугольников
и
вписана
окружность. Прямая, проходящая через вершину
и центр одной из окружностей, пересекает сторону
в точке
При этом
и
Аналогично, прямая, проходящая через вершину
и центр второй окружности, пересекает сторону
в точке
При этом
и
(b) Найдите длины сторон и
если дополнительно известно, что данные окружности касаются друг друга.
Пункт а), подсказка 1
Так ли проста прямая, соединяющая центр вписанной окружности с вершиной треугольника?) Просят найти AB/CD, а какие вообще отношения с AB и CD можно записать?
Пункт а), подсказка 2
Прямые BM и DN это биссектрисы треугольников! Тогда стоит воспользоваться свойством биссектрисы, чтобы связать отношениями AB с CD
Пункт б), подсказка 1
Мы уже знаем отношение AB/CD, так что хочется попробовать как-то с помощью переменных выразить AB и CD, чтобы потом решить уравнение.
Пункт б), подсказка 2
На рисунке есть окружности и касательные, на что это может намекать?
Пункт б), подсказка 3
Отрезки касательных к окружности из одной точки равны! Так что мы можем все отрезки, в том числе и AB и CD, выразить через отрезки, выходящие из вершин B и D.
![]()
(a) Так как биссектриса треугольника делит его сторону пропорционально двум другим сторонам, то
Следовательно,
(b) Обозначим точки касания окружности, вписанной в треугольник с его сторонами
через
соответственно; точки касания окружности, вписанной в треугольник
с его сторонами
— через
соответственно
(по условию точка касания со стороной
общая).
![]()
Пусть Используя равенство отрезков касательной, проведённых к окружности из одной точки, получаем
соотношения
В пункте (а) было получено, что откуда
Тогда
Ошибка.
Попробуйте повторить позже
На продолжении стороны треугольника
за точку
отмечена точка
такая, что
Найдите площадь
треугольника
если известно, что
Источники:
Подсказка 1
Угол BAC - внешний для треугольника BAT! Какие выводы можно сделать, пользуясь этим знанием и условием на углы BAC, BTC?
Подсказка 2
Верно, равнобедренность ABT. Далее нам было бы здорово сделать какие-то выводы про наш треугольник CBT, пользуясь доказанным фактом и тем, что AB = AC по условию
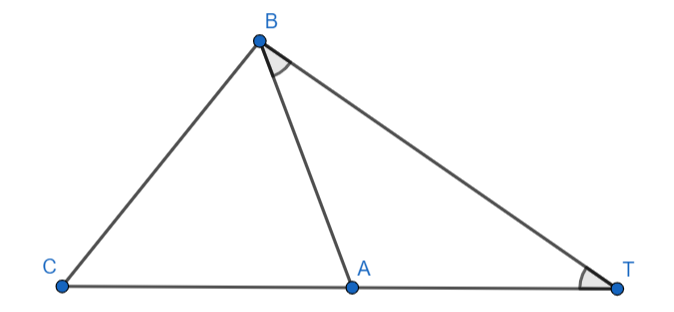
Поскольку — внешний для треугольника
то из условия получаем
Тогда
и
прямой. Отсюда по теореме Пифагора
и
Ошибка.
Попробуйте повторить позже
Четырёхугольник вписан в окружность радиуса
. Лучи
и
пересекаются в точке
, а лучи
и
пересекаются
в точке
. Известно, что треугольники
и
подобны (вершины не обязательно указаны в соответствующем
порядке).
(b) Пусть дополнительно известно, что окружности, вписанные в треугольники и
, касаются отрезка
в точках
и
соответственно, причём
(точка
лежит между
и
). Найдите
и площадь четырёхугольника
.
Источники:
Пункт а), подсказка 1
Заметим, что угол А у наших подобных треугольников общий. Что тогда можно сказать про другие углы этих треугольников?
Пункт а), подсказка 2
Ура! Мы использовали подобие, чтобы указать на равные углы! Но у нас два варианта… Как понять, что один не подходит?
Пункт а), подсказка 3
Да, угол ADP больше чем угол AQB. Значит, нам подходит только вариант равенства углов ABQ и ADP. Попробуйте, воспользовавшись вписанностью ABCD, понять, чему равен каждый из этих углов , и задача будет решена!
Пункт б), подсказка 1
Поскольку CK:KT:TA=6:1:7, то CT=TA, но ведь CA-диаметр из пункта а. Что это дает?
Пункт б), подсказка 2
Да, мы поняли, что угол DAC=45° (значит, мы нашли и площадь треугольника ADC). А также нашли длины отрезков CK,KT,TA. Воспользовавшись свойством равенства длин касательных из одной точки, попробуйте понять, как можно сделать картинку жёсткой. То есть какую одну переменную нужно ввести, чтобы картинка задавалась единственным образом?
Пункт б), подсказка 3
Да, радиус окружности, вписанной в треугольник ABC, фиксирует картинку. Осталось понять, чему равен этот радиус. Как это сделать? Попробуйте выразить площадь треугольника ABC двумя разными способами через радиус.
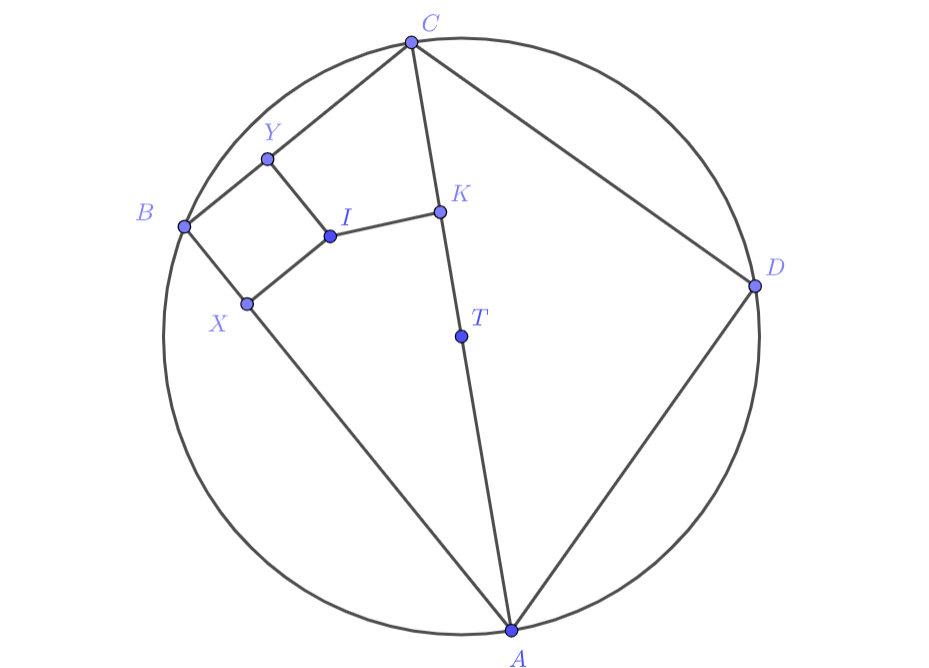
(a) Подобие треугольников эквивалентно равенству всех их углов. Так как угол при вершине у треугольников общий, то есть два
варианта: либо
либо
Второй случай невозможен, так как
внешний угол треугольника
поэтому он равен сумме
т.е.
Тогда остаётся первый случай и
Но четырёхугольник
вписан в окружность, а значит,
откуда
Следовательно,
диаметр окружности,
(b) Из предыдущего пункта получаем , то есть точка касания вписанной окружности является серединой стороны и
равнобедренный, откуда
. Пусть
— радиус вписанной окружности
и
— точки касания её
с катетами. Из условия
и
. При этом
, запишем площадь
двумя
способами
Поскольку , то
и
. Площадь равнобедренного
равна
,
откуда
.
Ошибка.
Попробуйте повторить позже
Подсказка 1
Что можно сказать про угол между хордой и касательной?
Подсказка 2
Верно, такой угол равен одному из вписанных углов, опирающихся на ту же дугу! Одной из задач, которая перед нами стоит, является найти радиус описанной окружности. В какой теореме он присутствует?)
Подсказка 3
Да, в теореме синусов!) Запишите ее и посмотрите, сколько приятных вещей можем из нее найти!
Подсказка 4
Посмотрите на треугольник АВD и найдите сторону АВ!
Подсказка 5
Воспользуйтесь синусом угла АВС, чтобы найти нужное нам расстояние!
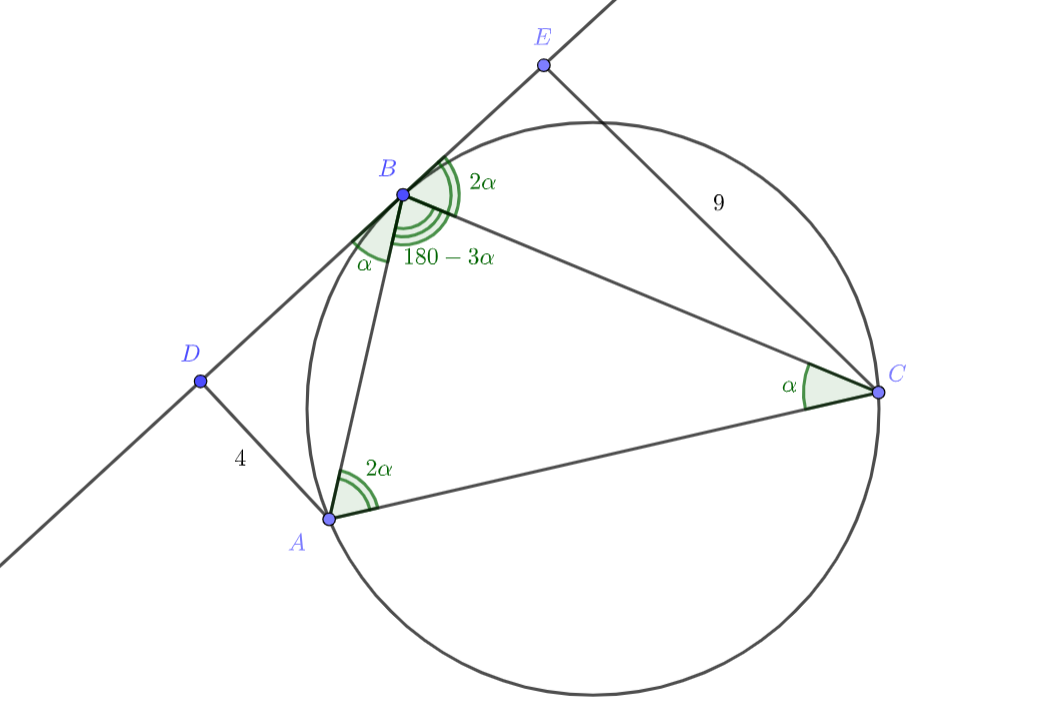
Пусть и
, где
— касательная. Учтём равенство углов между касательной и хордой вписанным, запишем
через
стороны
и
Поскольку , то
. Отсюда сразу же находим
Осталось найти высоту, для этого заметим следующее
а) 5
б)
Ошибка.
Попробуйте повторить позже
Равнобедренный треугольник с основанием
вписан в окружность
Хорды
и
параллельные прямой
пересекают сторону
в точках
и
соответственно, и при этом
. Найдите радиус окружности
и площадь
треугольника
если
а центр
окружности
расположен между прямыми
и
Источники:
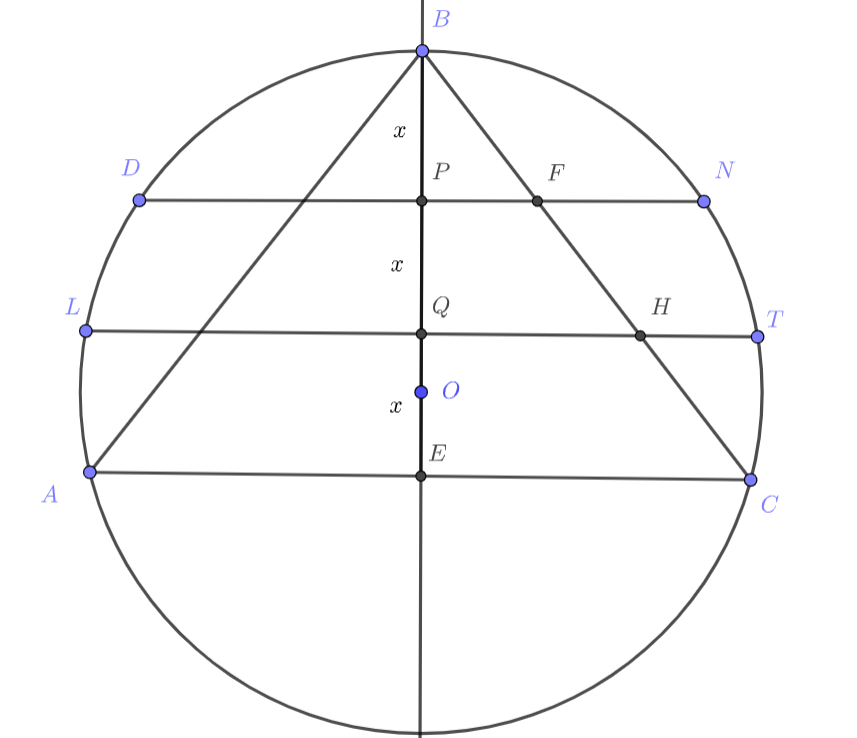
Прямая перпендикулярна хордам
и делит каждую из них пополам. Пусть точки
,
и
середины
и
Обозначим радиус окружности
за
Тогда
и по теореме
Пифагора для треугольников
и
получаем
откуда после раскрытия скобок и
приведения подобных слагаемых следует, что
находим, что ,
. Тогда
;
Вычитая из первого уравнения второе, находим, что ,
. Тогда
Следовательно, .
Ошибка.
Попробуйте повторить позже
В углы и
треугольника
вписаны соответственно окружности с центрами
и
равного радиуса, точка
— центр
окружности, вписанной в треугольник
Данные окружности касаются стороны
в точках
и
соответственно, при этом
и
(b) Пусть окружность с центром касается стороны
в точке
Найдите угол
если известно, что точка
является центром окружности, описанной около треугольника
Источники:
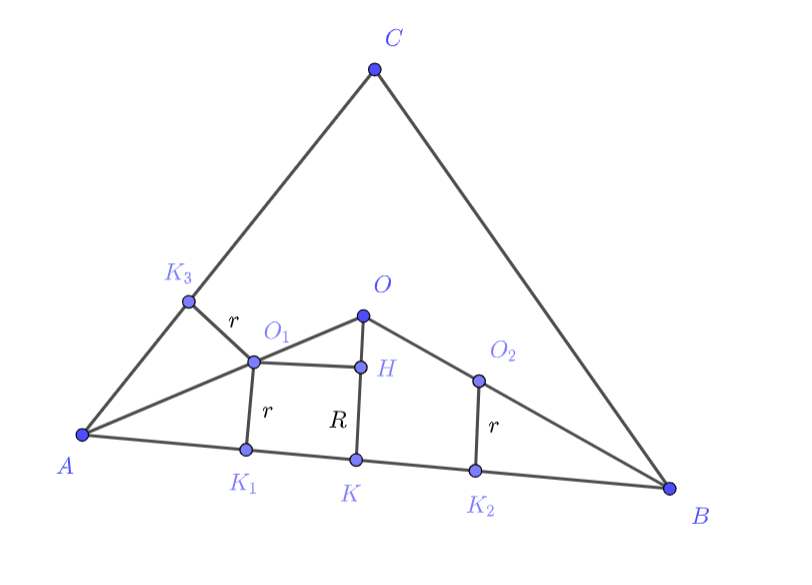
(a) Прямые и
являются биссектрисами углов
и
треугольника, поэтому они пересекаются в точке
- центре
вписанной окружности. Обозначим радиусы окружностей с центрами
и
через
а радиус вписанной окружности через
Треугольники
и
подобны, коэффициент подобия равен
поэтому
Аналогично
откуда
(b) Из условия следует, что Опустим из точки
перпендикуляр
на отрезок
Тогда
Значит,
Ошибка.
Попробуйте повторить позже
Две окружности разных радиусов касаются внешним образом. К ним проведены две общие внешние касательные и
Их точки
касания с меньшей окружностью —
и
с большей окружностью —
и
Найдите радиусы окружностей, если известно, что
,
Источники:
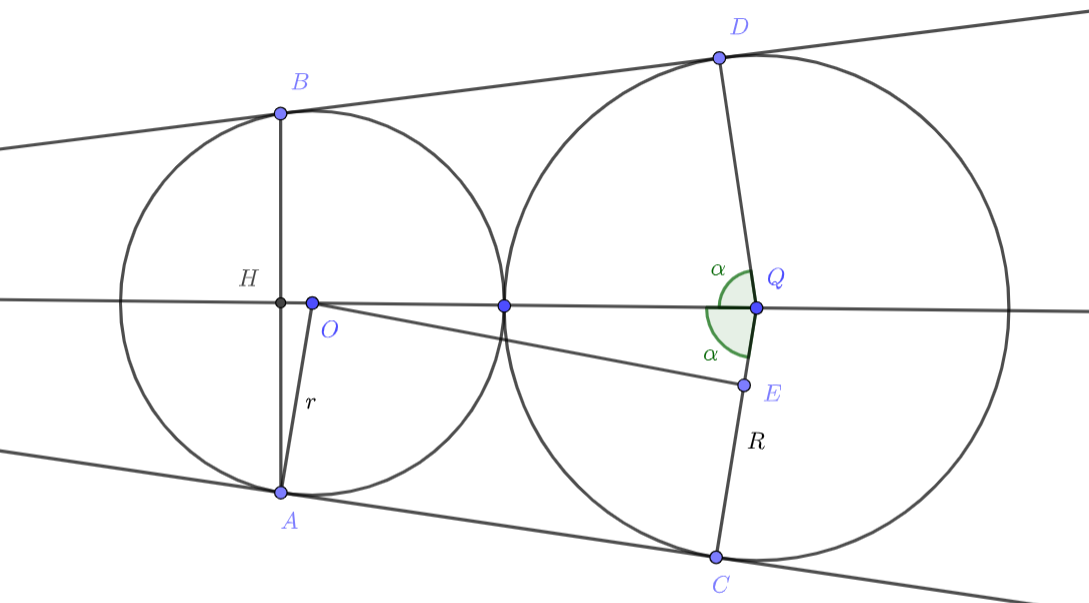
Введём обозначения: — центр меньшей окружности,
— центр большей окружности,
— радиус меньшей окружности,
радиус большей окружности,
Рассмотрим прямоугольную трапецию
Из точки
опустим перпендикуляр
на отрезок
Из прямоугольного треугольника
по теореме Пифагора получаем, что
Решая полученные
уравнения, находим, что
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике основание
равно
угол
равен
. Точка
лежит на стороне
так, что
площадь треугольника
вчетверо больше площади треугольника
Найдите расстояние от точки
до прямой
и радиус
окружности, описанной около треугольника
Источники:
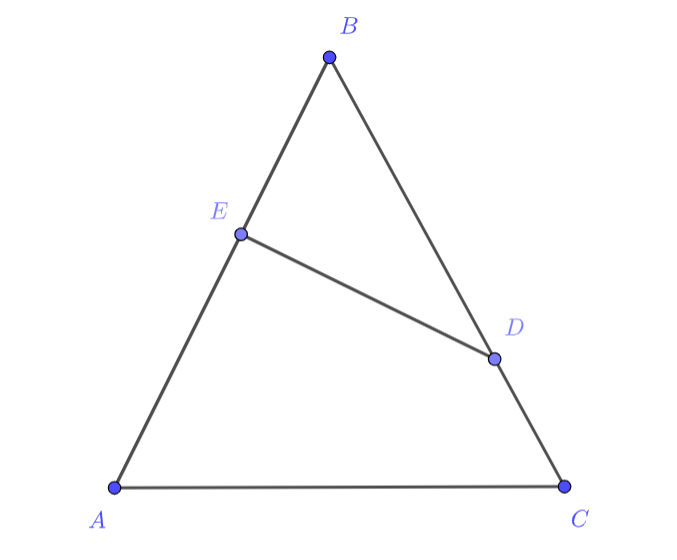
Пусть — проекция точки
на прямую
Так как
Следовательно, и
Имеем
(можно использовать
). Тогда
и
— расстояние от точки
до прямой
Далее, по теореме косинусов из
получаем
Следовательно, радиус окружности, описанной около треугольника равен
Ошибка.
Попробуйте повторить позже
В треугольнике медиана
угол
равен
угол
равен
Найти стороны
и биссектрису
треугольника
Источники:
Подсказка 1
Нам даны арктангенсы, но ведь с ними крайне неудобно работать. Давайте сразу найдем синусы и косинусы заданных углов. При этом, если смотреть на треугольники, на которые разбивается ABC медианой, то можно понять, что у нас много равных элементов в них. Синусы смежных углов, общая сторона и равные стороны. На что это может намекать?
Подсказка 2
На теорему синусов, для двух этих треугольников, ведь из теоремы синусов, правильно поперенося сомножитель, можно получить AB/BC = sin(ABM)/sin(CBM). А что это дает, если знать, что сумма площадей двух наших треугольников равна площади ABC?
Подсказка 3
Верно, если мы распишем площади как произведение сторон на синус угла между ними и поделим на 2 (не зря же мы эти соотношения с синусами находили), то выразим AB через BM и углы. А значит, нашли AB и BC. Осталось найти длину биссектрисы. Как это сделать зная весь треугольник? Как угодно. Однако, изысканный читатель скажет что…
Подсказка 4
Что есть формула биссектрисы! Мы же знаем все стороны треугольника, а значит, и отношения, в котором делит сторону биссектриса. Значит, и отрезки на которые биссектриса эту сторону разбивает. Однако, если вы не знаете эту формулу, то можно просто найти через теорему синусов угол A, а также найти через теорему синусов, но уже для треугольника ABE. А отрезок AE нетрудно найти из основного свойства биссектрисы. Остаётся посчитать :)
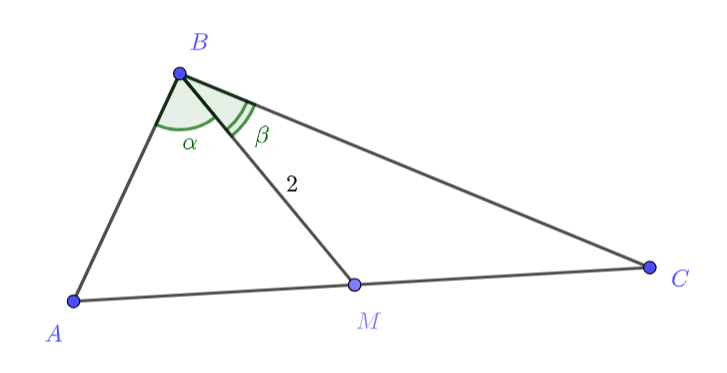
Обозначим
По теореме синусов из треугольников
и
находим
и
Так как и
то
В силу , имеем
По доказанному , откуда
т. e. Тогда
В нашем случае Тогда
,
Следовательно,
Длину биссектрисы можно найти из применения теорем косинусов для и
, а затем написав отношение полученных
выражений
Ошибка.
Попробуйте повторить позже
Медиана и биссектриса
прямоугольного треугольника
пересекаются в точке
Найти площадь треугольника
, если
Источники:
Подсказка 1
Сходу непонятно, что делать. У нас имеется медиана, почему бы ее не удвоить...
Подсказка 2
Обозначим за K- точку, симметричную A относительно M. Тогда видно, что треугольники △AOD и △COK подобны с коэффициентом 5/9. Тогда AD/CK=5/9 ⇒ AD/BD=5/4. Можем ли мы найти sin∠A-?
Подсказка 3
По свойству биссектрисы получаем, что sin∠A=BC/AC=4/5. Тогда cos∠A=3/5. Если обозначить AB за 9c, то AC=15c и BD=4с. Тогда из теоремы Пифагора для треугольника △BDC мы можем найти с. Я верю, что и площадь вы легко найдете!
![]()
На продолжении медианы за точку
отложим отрезок
, равный
. Тогда
— параллелограмм.
Обозначим . Треугольники
и
подобны (по двум углам), значит
По свойству биссектрисы треугольника
Поэтому
По теореме Пифагора
Следовательно,
Ошибка.
Попробуйте повторить позже
Биссектриса и высота
остроугольного треугольника
пересекаются в точке
. Окружность радиуса
с центром в точке
проходит через вершину
, середину стороны
и пересекает сторону
в точке
такой, что
. Найти длину
стороны
.
Подсказка 1
Исходя из условия, сразу хочется отметить пересечение луча AD с окружностью за точку F. Для удобства обозначим отрезки на AC с помощью переменной. Как посчитать отрезки на AB?
Подсказка 2
Пусть M — середина стороны AC. AK=AM, значит, BK = 6a, AK = 2a, AE = EM = a, MC = 2a. На что нам намекает равенство углов BAO и OAE, как использовать удвоенный угол и перпендикулярность?
Подсказка 3
Посчитаем косинус BAE! Тогда мы можем посчитать и косинус угла, в два раза меньшего BAE. Выходит, теперь у нас есть косинус угла, противоположного нужной стороне. А как можно найти саму сторону?
Подсказка 4
Найдем a благодаря косинусу и прямоугольному треугольнику! Теперь мы знаем 2 стороны и угол между ними - осталось лишь найти BC
Пусть — середина стороны
–– пересечение продолжения радиуса
с окружностью. Тогда
–– диаметр окружности.
Поскольку
— основание перпендикуляра, опущенного из точки
на хорду
точка
–– середина
Обозначим
Тогда
Точки и
лежат на окружности с диаметром
поэтому
Из равенства прямоугольных треугольников
и
(по гипотенузе и острому углу) следует, что
Тогда
Обозначим
![]()
Из прямоугольного треугольника находим, что
Тогда
Из прямоугольного треугольника находим, что
По теореме косинусов



