Ошибка.
Попробуйте повторить позже
В треугольнике медиана
угол
равен
угол
равен
Найти стороны
и биссектрису
треугольника
Источники:
Подсказка 1
Нам даны арктангенсы, но ведь с ними крайне неудобно работать. Давайте сразу найдем синусы и косинусы заданных углов. При этом, если смотреть на треугольники, на которые разбивается ABC медианой, то можно понять, что у нас много равных элементов в них. Синусы смежных углов, общая сторона и равные стороны. На что это может намекать?
Подсказка 2
На теорему синусов, для двух этих треугольников, ведь из теоремы синусов, правильно поперенося сомножитель, можно получить AB/BC = sin(ABM)/sin(CBM). А что это дает, если знать, что сумма площадей двух наших треугольников равна площади ABC?
Подсказка 3
Верно, если мы распишем площади как произведение сторон на синус угла между ними и поделим на 2 (не зря же мы эти соотношения с синусами находили), то выразим AB через BM и углы. А значит, нашли AB и BC. Осталось найти длину биссектрисы. Как это сделать зная весь треугольник? Как угодно. Однако, изысканный читатель скажет что…
Подсказка 4
Что есть формула биссектрисы! Мы же знаем все стороны треугольника, а значит, и отношения, в котором делит сторону биссектриса. Значит, и отрезки на которые биссектриса эту сторону разбивает. Однако, если вы не знаете эту формулу, то можно просто найти через теорему синусов угол A, а также найти через теорему синусов, но уже для треугольника ABE. А отрезок AE нетрудно найти из основного свойства биссектрисы. Остаётся посчитать :)
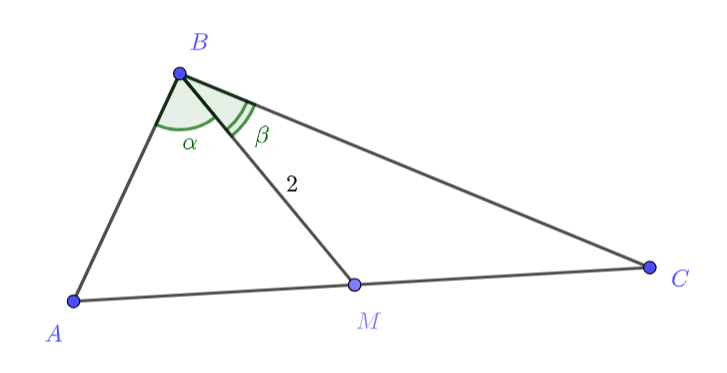
Обозначим
По теореме синусов из треугольников
и
находим
и
Так как и
то
В силу , имеем
По доказанному , откуда
т. e. Тогда
В нашем случае Тогда
,
Следовательно,
Длину биссектрисы можно найти из применения теорем косинусов для и
, а затем написав отношение полученных
выражений
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное обучение
в Школково
Для детей ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Брянской областей, а также школьникам, находящимся в пунктах временного размещения Крыма обучение на платформе бесплатное.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ или олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




