Ошибка.
Попробуйте повторить позже
100 человек пришли на представление в шляпах. Фокусник поменял местами их шляпы. После этого каждую минуту каждый человек
находил свою шляпу и передавал тому, у кого эта шляпа в данный момент находилась, ту шляпу, которая в этот момент была у
него самого. (Если на каком-то шаге у человека оказывается шляпа, принадлежащая человеку
, а у человека
оказывается шляпа, принадлежащая человеку самому
, то на следующем шаге у
оказывается шляпа, принадлежащая
).
Фокусник изначально раздал шляпы так, чтобы в итоге они вернулись к своим настоящим хозяевам, но при этом это произошло бы как можно позже. Через сколько минут, самое позднее, это может произойти в первый раз?
Источники:
Подсказка 1
Условие про то, как передвигаются шляпы достаточно сложное, поэтому, чтобы хорошо его понять, нужно самому подвигать шляпы на каком-то количестве человек. Давайте рассмотрим какого-то человека А₀, так как мы сами вводим обозначения, то давайте изначально его шляпа была у А₁. Тогда человека, держащего шляпу А₁, назовём А₂ и так далее. В какой момент цепочка А₀- А₁-А₂ остановится? Обязательно поймите, почему это точно произойдёт.
Подсказка 2
Цепочка остановится в момент, когда шляпа какого-то Аₙ₋₁ окажется у Aₖ, которого мы уже записывала в нее. Тогда чему может быть равно k?
Подсказка 3
Через минуту шляпа А₀ окажется у того, кто держал раньше шляпу А₁, то есть у А₂, шляпа А₁ будет у А₃. Тогда можно сделать вывод, что для каждого k шляпа Aₖ через минуту окажется у Aₖ₊₂.
Подсказка 4
Через m минут шляпа Aₖ будет находиться у человека с номером k + 2ᵐ. Тогда при каком количестве человек шляпа сможет вернутся к исходному владельцу? Воспользуйтесь тем, что Aₖ = Аₙ₊ₖ.
Подсказка 5
Шляпа может вернуться к исходном владельцу только в случае, если количество человек в цикле является степенью двойки! По условию фокусник изначально раздал шляпы так, чтобы в итоге они вернулись к своим настоящим хозяевам. Это значит, что все 100 человек разобьются на некоторое количество циклов (цикл из одного человека тоже может быть). Но мы уже получили условие на длины циклов. Тогда какая может быть наибольшая, учитывая ограничение в 100 человек?
Рассмотрим некоторого человека, назовём его . Пусть его шляпа изначально оказалась у какого-то
, шляпа
оказалась у
, и
т.д. Рассмотренный нами процесс нумерации рано или поздно закончится тем, что для какого-то
его шляпа окажется у какого-то
, который был уже нами пронумерован ранее. При этом это может быть только
, т.к. про всех остальных мы уже знаем, откуда
взялись находящиеся у них шляпы.
Значит, шляпа в начале представления оказалась у
и мы получили так называемый цикл из
человек. Для удобства будем
считать, что
и т.д., чтобы иметь возможность говорить, что каждый человек с номером
передал свою шляпу
человеку с номером
(то есть, мы на самом деле нумеруем людей остатками (классами вычетов) при делении на
).
После того, как джентльмены передадут свои шляпы, шляпа окажется у того, у кого раньше была шляпа
, то есть у
, шляпа
окажется у
и т.д. Шляпа каждого
окажется у
. После второй передачи шляпа каждого
окажется у
и т.д.
Через
минут шляпа
окажется у
.
Если это тот же человек, что и , разность их номеров, то есть
, должна делится на
. Значит, шляпа может вернуться к
исходном владельцу, только если количество человек в цикле является степенью двойки. При этом фокусник хочет, чтобы был цикл как
можно большей длины.
Самая большая степень двойки, не превосходящая 100, это . Фокусник в начале должен разбить пришедших на представление на
циклы, длины одного из которых равна 64, а длины остальных — меньшие степени двойки, не важно какие. Тогда через 6 минут все шляпы
окажутся у своих настоящих владельцев (у некоторых они окажутся раньше, но в этот момент это впервые произойдёт для всех
сразу).
Ошибка.
Попробуйте повторить позже
Клетчатый куб состоит из ячеек, представляющих из себя единичные кубики. 361 ячейка закрашена. Докажите, что в каком-то
кубике
закрашено хотя бы четыре ячейки.
Источники:
Подсказка 1
Дан куб со стороной 9, а надо понять что-то про кубики со стороной 2. Конечно, неудобно, что большой куб ровно не разбиваются на маленькие. Но мы можем попробовать разбить на кубики 2*2*2 хотя-бы ту часть куба, которую возможно, и применить для нее предположение, противоположное вопросу задачи.
Подсказка 2
Но у нас остается еще часть большого куба, не разбитая на кубы 2*2*2. Эту часть тоже можно как-то разбить хорошо (удобно, что 4 ячейки укладываются в квадратик 2*2) и понять, какое максимальное кол-во закрашенных ячеек может быть, если в каждом кубике 2*2*2 их не более 3!
Вырежем из нашего куба куб и разобьём его на 64 куба
.
Предположим, что в каждом кубике закрашено не более трёх ячеек, то есть всего не более 192.
В исходном кубе после этого остались кубики на трёх гранях, имеющих общую вершину. Рассмотрим 64 клетки на одной из этих граней,
которые не лежат ни на какой из двух других. Они разбиваются на 16 квадратов , в каждом из которых не более трёх закрашенных
ячеек. Итого на трёх гранях получаем не более
.
У нас остались не рассмотренными 25 ячеек, образующих три ребра исходного куба, сходящиеся в одной вершине. Среди них закрашены
не более 24, так как общая ячейка трёх этих рёбер и три её соседних лежат в одном кубике , значит, среди этих четырёх ячеек не
более трёх закрашенных.
Таким образом, мы получаем максимум закрашенных ячеек, что противоречит условию задачи. Значит, наше
предположение было неверно.
Ошибка.
Попробуйте повторить позже
На бесконечной клетчатой плоскости некоторые клетки покрашены в красный цвет, некоторые — в синий, а некоторые остались непокрашенными. Известно, что в каждой строчке, где есть хотя бы одна синяя клетка, есть также хотя бы 5 красных, а в каждом столбце, где есть хотя бы одна красная клетка, есть хотя бы 6 синих. Какое наименьшее положительное число покрашенных клеток может быть на плоскости?
Источники:
Подсказка 1
Для начала заметим, что мы можем избавиться от всех столбцов, в которых все клетки синие и от всех строк, в которых все клетки красные. Теперь в каждом столбце и строке у нас и синие, и красные клетки. Пусть у нас есть m строк и n столбцов ,x-кол-во красных клеток, y-кол-во синих клеток. По условию в каждом столбце хотя бы 6 синих клеток => y>=6n, аналогично x>=5m. В каждой строке есть хотя бы одна синяя клетка и 5 красных, n>=6.Аналогично m>=7.Чтобы догадаться до ответа, бывает полезно рассмотреть частный случай. Попробуйте рассмотреть случай, когда все закрашенные клетки будут находиться только на пересечении строк и столбцов.
Подсказка 4
Так как n<=9 и x>=60, то в каком-то столбце >=7 красных клеток, тогда в каком-то столбце >=13 клеток, тогда m>=13 и x>=65 и y<55. Вам не кажется это похожим на предыдущий шаг? Попробуйте теперь сами сделать то же самое.
Подсказка 5
После нескольких таких шагов мы получим, что n<=5, но у нас n>=6. Противоречие! Со вторым случаем делаем то же самое. Оценка доказана. Значит, наш ответ 120.
Примеров для 120 закрашенных клеток несколько, они все отличаются перестановкой строк и столбцов. Можно взять прямоугольник
и раскрасить его в шахматном порядке в красный и синий цвет.
Докажем теперь, что меньше 120 закрашенных клеток не может быть.
Если в каком-то столбце есть закрашенные клетки, то по условию они либо только синие, либо обоих цветов. При этом, если в каком-то столбце все закрашенные клетки синие, можно превратить их все в незакрашенные. При этом условие задачи сохранится, а количество закрашенных клеток уменьшится (но не до нуля, так как в строчках с этими синими клетками останутся какие-то красные). Аналогичным образом можно избавиться от строчек, в которых есть красные клетки, но нет синих. Теперь можно считать, что во всех строчках и столбцах, где есть закрашенные клетки, присутствуют клетки обоих цветов.
Пусть у нас красных клеток и
синих, при этом закрашенные клетки находятся в
строках и
столбцах. Так как в каждом из
этих
столбцов присутствуют хотя бы 6 синих клеток, выполняется неравенство
или, что то же самое,
Аналогично,
или, что то же самое,
Также заметим, что в каждой строке есть хотя бы одна синяя клетка и 5 красных,
Аналогично
Сравним числа и
Пусть то есть
В каждом столбце присутствуют хотя бы 6 синих клеток. Из взятого в качестве предположения
неравенства следует, что в каком-то столбце количество красных клеток хотя бы
от количества синих, то есть хотя
бы 5, поэтому общее количество закрашенных клеток в данном столбце хотя бы 11, откуда
и, следовательно,
Если
и оценка доказана. Предположим,
тогда
то есть не превосходит
10.
Но раз а
в каком-то из наших не более чем 10 столбцов присутствуют хотя бы 6 красных клеток. Так как в нём должно
быть ещё и 6 синих, мы получаем, что общее количество закрашенных клеток в этом столбце хотя бы 12, то есть,
и
Тогда, чтобы
было меньше 120, необходимо
Продолжим эти рассуждения.
Поскольку значит
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 7 красных клеток, откуда
Поскольку в каком-то столбце присутствуют хотя бы
то есть хотя бы 8 красных клеток, откуда
Поскольку значит,
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 9 красных клеток, откуда
Поскольку значит,
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 11 красных клеток, откуда
Поскольку значит,
Значит, в каком-то столбце присутствуют хотя бы
то есть хотя бы 15 красных
клеток, откуда
Отсюда получаем, что
что противоречит доказанному
ранее.
Аналогично разбираем случай, когда то есть
В каждой строке присутствуют хотя бы 5 красных клеток. Из взятого в
качестве предположения неравенства следует, что в какой-то строке есть хотя бы 6 синих клеток, то есть общее количество закрашенных
клеток в данной строке хотя бы 11, откуда
и, следовательно,
Если
и оценка доказана. Предположим,
тогда
то есть не превосходит 10.
Но раз а
в какой-то из наших не более чем 10 строк присутствуют хотя бы 7 синих клеток. Так как в ней должно быть
ещё и 5 красных, мы получаем, что общее количество закрашенных клеток в этой строке хотя бы 12, то есть,
и
Тогда,
чтобы
было меньше 120, необходимо
Продолжим эти рассуждения.
Поскольку в какой-то строке присутствуют хотя бы
то есть хотя бы 8 синих клеток, откуда
Поскольку значит
Значит, в какой-то строке присутствуют хотя бы
то есть хотя бы 10 синих
клеток, откуда
Отсюда получаем, что
что противоречит доказанному
ранее.
Таким образом, мы разобрали оба случая и доказали, что ситуация, в которой невозможна.
Ошибка.
Попробуйте повторить позже
На конференцию приехали учёных. Оказалось, что у любых двоих как минимум двое общих знакомых. Докажите, что у кого-то из них
хотя бы
знакомых.
Источники:
Предположим противное. Рассмотрим граф, вершинами которого будут являться учёные, две вершины будем соединять ребром, если
соответствующие учёные знакомы. Из нашего предположения степень каждой вершины не превосходит . Посчитаем двумя способами
количество растопырок, то есть конфигураций из
вершин, одна из которых (будем называть её главной) соединена с двумя
другими). С одной стороны для каждой пары вершин к ним в растопырку можно выбрать хотя бы
главные. Итого
растопырок не меньше, чем
. С другой стороны для каждой вершины количество растопырок, в которых она
является главной, не превосходит
. То есть всего растопырок не больше
, откуда получаем
противоречие.
Ошибка.
Попробуйте повторить позже
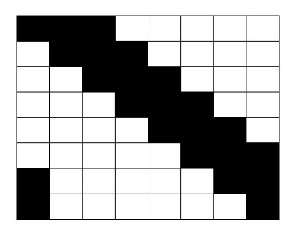
В таблице какие-то
клетки чёрные, а остальные — белые. В каждой белой клетке написали суммарное количество чёрных,
находящихся с ней на одной горизонтали и находящихся с ней на одной вертикали; в чёрных клетках ничего не написано. Какое наибольшее
значение может принимать сумма чисел во всей таблице?
Источники:
Подсказка 1
Очень часто в задачах, где нужно считать сумму чисел, помогает рассмотреть ситуацию отдельно для горизонталей и для вертикалей. Так как нам нужен максимум суммы чисел во всей таблице, то попробуем найти максимум для суммы чисел на горизонталях и на вертикалях.
Подсказка 2
Пусть в строке находится x черных 8-x белых. Теперь мы можем посчитать сумму во всех строках. Для того чтобы максимизировать такую сумму, нам нужно минимизировать сумму восьми квадратов с фиксированной суммой. Как?
Подсказка 3
Сумма квадратов чисел уменьшается при сближении этих чисел к их среднему арифметическом, поэтому для целых чисел минимум достигается, когда семь из восьми чисел равны 3, а оставшееся равно 2. Теперь мы можем проделать аналогичные действия с вертикалями и построить пример!
Число в белой клетке состоит из двух слагаемых: "горизонтального"и "вертикального". Рассмотрим отдельно сумму всех "горизонтальных"и отдельно сумму всех "вертикальных"слагаемых по всей таблице. Если мы максимизируем каждую из этих двух сумм по отдельности, общая сумма также будет наибольшей.
Рассмотрим сумму "горизонтальных"слагаемых. Если в строке находится чёрных клеток и
белых, то сумма горизонтальных
слагаемых в этой строке составляет
. Просуммировав эту сумму по всем строкам, мы получаем
Нам нужно максимизировать это выражение, т.е. минимизировать сумму квадратов восьми чисел, сумма которых составляет 23. Как известно, сумма квадратов чисел уменьшается при сближении этих чисел к их среднему арифметическом, поэтому для целых чисел минимум достигается, когда семь из восьми чисел равны 3, а оставшееся равно 2.
Таким образом, мы получаем, что наименьшая возможная сумма "горизонтальных"слагаемых равна
Аналогичную оценку можно получить для суммы "вертикальных"слагаемых, что даёт нам итоговое значение 234.
Осталось убедиться, что существует раскраска таблицы, при которой обе суммы максимальны одновременно, то есть в которой в каждом столбце или строке по 2 или 3 закрашенных клетки.
Ошибка.
Попробуйте повторить позже
Дан правильный -угольник
в котором проведены все диагонали. Докажите, что они образуют не больше
точек пересечения (не считая вершин).
Источники:
Подсказка 1
Нам дали уж слишком какое-то магическое число, но каждое его слагаемое похоже на какой-то комбинаторный подсчёт. Может быть, у нас получится объяснить, как получить каждое из этих слагаемых?
Подсказка 2
1-ое слагаемое: эта формула нам так и кричит, что в ней выбрали 4 вершины многоугольника без учёта их порядка. А как выбор 4-ёх вершин связан с диагоналями?
Подсказка 3
2-ое слагаемое: с помощью какого предположения было получено первое слагаемое? Заметьте, что почти каждое следующее слагаемое стоит со знаком минус, а значит, они как-то уточняют нашу первоначальную оценку.
Подсказка 4
2-ое слагаемое: давайте вспомним, что у нас в условии правильный многоугольник, попробуйте порисовать разные правильные многоугольники и диагонали в них, чтобы найти такую точку, в которой всегда пересекаются много диагоналей, что это за точка?
Подсказка 5
2-ое слагаемое: верно, это центр нашего многоугольника. Остаётся только посчитать, сколько раз мы посчитали её и вычесть так, чтобы по итогу в нашем подсчёте точка осталась учтена.
Подсказка 6
3-е слагаемое: оно явно содержит похожие диагонали на те, которые мы выбирали, когда рассуждали про центр, потому что в нём тоже фигурирует n/2. Может быть стоит опять порассуждать про такие диагонали?
Подсказка 7
3-е слагаемое: первый множитель в слагаемом это n/2, давайте тогда зафиксируем какую-то диагональ, проходящую через центр многоугольника. Попробуйте понять, что означают остальные множители, последовательно распутывая, за что отвечает каждый из множителей.
Подсказка 8
3-е слагаемое: верно, слева и справа от диагонали осталось по n/2-1 точке. А значит, вторым действием мы скорее всего выбрали с одной из сторон одну из точек. Почему тогда последний множитель не такой же, а имеет на 2 точки меньше? Понятно, что, выкинув 2 точки с другой стороны, мы запретили какие-то 2 диагонали, остаётся понять - какие?
Подсказка 9
3-е слагаемое: кажется, что пока наши рассуждения задают только пару диагоналей и проблем не видно, но можно ли как-то для этой пары найти однозначно третью диагональ, которая бы проходила через их точку пересечения?
Подсказка 10
3-е слагаемое: да, можно, если отразить симметрично вторую диагональ относительно "центральной".
Подсказка 11
3-е слагаемое: а вы заметили, что на самом деле это слагаемое содержит в себе удвоенное количество ситуаций, про которые мы рассуждали? Ведь, когда мы брали диагональ-1 с концами по разные стороны от "центральной" диагонали и отражали её, то получалась диагональ-2, которая тоже может быть посчитана нашими рассуждениями, а так как симметричная для 2-ой диагонали - 1-ая, то мы посчитали всё дважды. А сколько раз мы посчитали такие ситуации в 1-ом слагаемом?
Подсказка 12
Верно, по 3 раза, потому что там мы выбираем неупорядоченную пару диагоналей, а в наших рассуждениях мы получали неупорядоченные тройки диагоналей (если учесть, что мы посчитали их дважды), а значит 1 наша тройка содержит по 3 пары. Но вычесть всё равно придётся удвоенное количество, поэтому мы победили!!!
Если бы все точки пересечения диагоналей были различны, для их подсчёта достаточно было бы посчитать общее количество способов
выбрать 4 вершины -угольника. Действительно, каждая пара пересекающихся диагоналей даёт нам 4 вершины; с другой стороны, для
каждых 4 вершин отрезок, соединяющий первую и третью по часовой стрелке, и отрезок, соединяющий вторую и четвёртую, будут
пересекающимися диагоналями (сторонами они не могут быть, так как стороны ни с чем не пересекаются). Количество таких способов
составляет
Однако, при таком подсчёте точки, в которых пересекаются больше двух диагоналей, посчитаны несколько раз.
Во-первых, поскольку количество вершин чётно, "длинных"диагоналей (соединяющий противоположные вершины многоугольника)
пересекаются в центре многоугольника. Эта точка посчитана
раз, в то время как должна быть посчитана 1 раз. Значит, из вычисленного количества надо вычесть
Во-вторых, для каждой "длинной"диагонали можно взять две симметричные относительно неё диагонали, не проходящие
через центр многоугольника. "Длинную"диагональ можно выбрать способами. Для удобства представим себе, что
выбранная диагональ расположена вертикально. По каждую сторону от этой диагонали остаётся
вершина. Мы выбираем
вершину
слева от “длинной” диагонали, после чего для выбора вершины
справа у нас остаётся
варианта: мы не
можем выбрать вершину, симметричную
относительно "длинной"диагонали (иначе диагональ
будет симметрична
сама себе) и вершину, симметричную относительно центра, иначе
будет "длинной а эти точки пересечения мы уже
учли.
Симметричная диагональ выбирается единственным образом. Однако каждую пару диагоналей
и
мы посчитали
дважды, потому что в качестве первой выбранной диагонали могла быть взята любая из них. Таким образом, точку пересечения трёх
диагоналей мы умеем искать
способами. В исходной формуле каждая такая точка посчитана трижды, то есть два лишних раза. Значит, мы получаем ещё на
точек меньше.
Вычитая из исходного количества пересечений оба эти выражения мы получаем в точности то, что и требовалось. Если какие-то точки, посчитанные в предыдущем абзаце, на самом деле совпадают, то вычитать надо ещё больше.
Ошибка.
Попробуйте повторить позже
На собрании присутствовали рыцари, всегда говорящие правду и лжецы, которые всегда лгут (точно есть и те, и другие). Каждый сказал:
“Я знаком хотя бы с рыцарями на этом собрании” и “Я знаком хотя бы с
лжецами на этом собрании”. Какое наименьшее количество
человек могло собраться?
Источники:
Рассмотрим произвольного рыцаря. Из его фразы следует, что на собрании рыцарей и
лжецов. Построим двудольный граф
знакомств рыцарей и лжецов, в первой доле вершины — рыцари, во второй — лжецы. Из каждой из хотя бы
вершин первой доли исходит
минимум
ребер, следовательно, ребер в графе
C другой стороны, лжец знаком не более, чем с
рыцарями, а значит,
если лжецов
то имеем
Приведем пример на рыцарей и
лжецов: пронумеруем рыцарей и лжецов. Рассмотрим первых
рыцарей. Пусть среди них
рыцари и лжецы с одинаковыми номерами будут не знакомы. А также со сдвигом на один: второй рыцарь не знаком с первым лжецом,
третий рыцарь со вторым и так далее. Все остальные знакомы, рыцари попарно знакомы между собой, а лжецы попарно не знакомы. Такая
ситуация подходит, так как каждый лжец не знаком хотя бы с двумя рыцарями, и каждый рыцарь знаком хотя бы с
лжецами.
Ошибка.
Попробуйте повторить позже
Сколькими разными способами можно в таблице расставить натуральные числа от 1 до 14 (все по одному разу) так, чтобы сумма
чисел в каждом из семи столбцов была нечётна?
Источники:
Подсказка 1
Какие должны быть два числа, чтобы их сумма была нечетной? Очевидно, одно - четным, другое - нечетным. Кстати, у нас всего 7 четных и 7 нечетных чисел. Сколько способов выбрать, какое по четности число будет в верхней клетке столбцов?
Подсказка 2
Конечно, выбираем из четного или нечетного числа - 2 способа заполнить столбец, но для каждой расстановки в первом столбце подходят все расстановки остальных столбцов, значит, применяем правило умножения и получаем коэффициент 2⁷. Теперь подумаем, сколько способов есть расставить все четные числа в одном из 2⁷ возможных вариантов по четности/нечетности.
Подсказка 3
7 чисел на 7 мест, причём важен порядок -> получили 7! способов. Но не кажется ли вам, что столько же способов и для нечетных чисел, ибо логика действий сохраняется и для них. А еще для каждой расстановки четных чисел подходят все расстановки нечетных чисел, следовательно, 7! возведётся в квадрат. Вспоминаем про коэффициент из 2 подсказки и получаем ответ.
В каждом столбце стоит одно чётное и одно нечётное число. Где стоит чётное число, а где нечётное, выбирается двумя способами, итого
способов для всей таблицы. Далее, существует
способов расставить чётные числа по выбранных для них местам и столько же способов
расставить нечётные. Итого
способов.
Ошибка.
Попробуйте повторить позже
Сколькими способами можно расставить натуральные числа от до
в квадратной таблице
так, чтобы сумма чисел в каждой
строке и в каждом столбце была чётна? (Числа могут повторяться)
Будем расставлять в таблицу нули и единицы. Каждый можно поставить четырьмя способами, а
— пятью. Заметим, что в каждой
строчке чётное количество единиц, потому единиц суммарно в таблице может быть
(
быть не может, поскольку в каждой
строчке не более двух). Также заметим, что двух единиц быть не может, поскольку тогда бы они стояли в одной строчке и их было бы по
одной в столбце. Разберём остальные случаи
- Пусть единиц нет. Тогда имеем
чётных чисел и
способов в этом случае.
- Пусть единиц четыре. Тогда они стоят на пересечении двух строчек и двух столбцов. Выбираем строчки и столбцы
способами, в итоге имеем
способов.
- Пусть единиц шесть. Тогда оставшиеся нули стоят в разных строчках (в каждой строчке и в каждом столбце должно быть
ровно по две единицы). Число способов так расставить нули равно
, откуда имеем
.
Ошибка.
Попробуйте повторить позже
В некоторой стране городов и
авиакомпаний. Каждые два города соединены рейсами одной из шести авиакомпаний. Можно ли
утверждать, что найдется авиакомпания и больше
городов, между любыми двумя из которых можно добраться рейсами этой
авиакомпании (возможно, с пересадками)?
Построим контрпример. Разобьём города на групп по
городов. Назовём эти группы
Внутри каждой группы соединим города рейсами компании номер
Компания номер будет соединять города группы
с городами группы
с
а
с
Компания номер будет соединять города группы
с городами группы
с
а
с
Компания номер будет соединять города группы
с городами группы
с
а
с
Компания номер будет соединять города группы
с городами группы
с
а
с
Компания номер будет соединять города группы
с городами группы
с
а
с
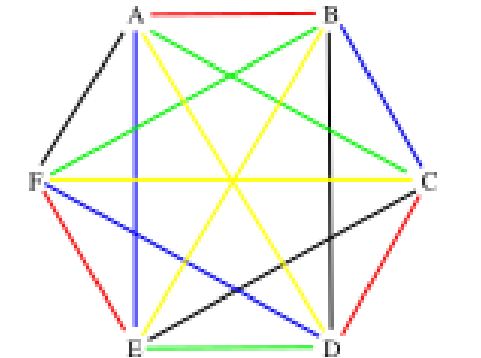
Таким образом, рейсы компании номер связывают по
городов, а рейсы остальных компаний ровно по
Это построение схематически изображено на рисунке. Разные компании обозначены разными цветами.
Нет
Ошибка.
Попробуйте повторить позже
В городе Джентльвилле живут джентльменов, любые двое из которых либо дружат, либо враждуют. В какой-то момент каждый
джентльмен попросил каждого из своих друзей послать открытку ненависти каждому из своих врагов (джентльмен
просит джентльмена
послать открытку всем врагам джентльмена
). Каждый из джентльменов выполнил все просьбы; при этом он посылал каждому из
своих врагов такое количество открыток, сколько раз его об этом просили. Какое наибольшее количество открыток могло быть
послано?
Источники:
Подсказка 1!
1) Так, было бы здорово оценить количество открыток как-то, в зависимости от количества друзей, чтобы попробовать посчитать максимум..... Например, если у человека друзей будет х, а врагов соответственно 14-х, то сколько открыток он пошлет?
Подсказка 2!
2) Так, хорошо, х(14-х)! Нужно понять, где это выражение принимает максимум, и проверить, получится ли наш максимум достигнуть... Было тут у нас какое-то утверждение про степени вершин в графе... Хм...
Подсказка 3!
3) Ага, вот оно! Лемма о рукопожатиях! Теперь идейно задачу решили, осталось только немного разобраться, как все же получить новый максимум!
Рассмотрим полный граф на вершинах, вершинами которого являются джентльмены, а рёбрами — отношения между ними. Покрасим
между двумя вершинами в белый цвет, если джентльмены, соответствующие этим вершинам дружат. А чёрные ребра будут символизировать
вражду между людьми.
Оценка.
Пусть у джентльмена с номером (
) ровно
друзей и
врагов (
). Тогда он отправил ровно
писем. Это выражение является квадратным трёхчленом, наибольшее значение которого достигается при
и равно
Тогда число отправленных всеми джентльменами писем не превосходит
Покажем, что отправить ровно писем невозможно по лемме о рукопожатиях (в любом графе количество вершин нечётной степени
чётно). Действительно, в таком случае у каждого джентльмена должно быть
друзей и
врагов. Рассмотрим подграф из всех вершин и
только белых рёбер. В этом подграфе количество рёбер (количество пар друзей среди джентльменов) равно половине от суммы степеней
вершин (у каждого по
друзей, но одну и ту же пару считаем дважды), то есть
Противоречие с тем, что это число должно быть
целым.
Пример.
Покажем, что отправить писем возможно. Достаточно построить “чёрный” подграф: нужно соединить каждого
джентльмена с тремя следующими — получим однородный граф степени
затем останется соединить каких-то
подряд с
джентльменами, которые идут на
позиций позже по кругу. То есть
Тогда степени первых
-и вершин станут равны
а у
-й она останется равной


