Пусть описанная окружность треугольника является единичной с центром в и треугольник положительно ориентирован. Заметим, что тогда Обозначим угол через Введем обозначение Тогда откуда Вычисляем

Обозначим через центр описанной окружности треугольника Заметим, что Тогда

Получаем, что ориентированный угол равен То есть откуда находим

То есть координата центра описанной окружности треугольника имеет вид где не зависят от а бегает по единичной окружности. Тогда понятно, что и бегает по окружности, полученной из единичной умножением на и сдвигом на

Пусть Поскольку любая степень числа дает остаток от деления на то сумма таких степеней дает остаток от деления на С другой стороны, степени числа дают лишь остатки или от деления на поэтому сумма степени числа может давать остаток от деления на только если все слагаемые равны Но тогда противоречие. Значит,

Для есть пример:

Первое решение. Покажем, что при данных условиях на многочлен каждая следующая точка касания лежит по другую сторону от оси чем предыдущая.

Пусть — данный многочлен, — его производная. Пусть — это -я точка касания, а -я. Тогда касательная в точке имеет уравнение Значит, откуда Разделив это равенство на и перенеся все слагаемые в правую часть, получим при четной степени выражение:

Пусть и одного знака (считаем, что с любым числом одного знака). Если то выражение в скобках положительно, если же то оно отрицательно. Такие же знаки будут иметь выражения при остальных степенях: Значит, если и одного знака, то равенство невозможно. Итак, любые две последовательные точки касания должны находиться по разные стороны от оси И в силу нечетности касательная в точке не может пройти через точку

Второе решение. Заметим, что функция при и нечетном выпукла на и вогнута на Многочлен представляется в виде суммы нескольких функций такого вида, потому что является нечетной функцией, а его коэффициенты неотрицательные. Тогда функция также выпукла на и вогнута на Это означает, что касательная в точке графика с положительной абсциссой вторично не пересекает график в точках с неотрицательной абсциссой, и наоборот. Кроме того, касательная к графику в нуле не имеет с ним больше общих точек. Это означает, что абсциссы точек отличны от нуля, а их знаки чередуются. Тогда у точек и абсциссы одного знака, поэтому касательная в точке не проходит через точку

Пусть описанная окружность треугольника является единичной с центром в нуле. Обозначим через комплексное число, отвечающее повороту на против часовой стрелки, через — отвечающее повороту на по часовой стрелке. Тогда центр вписанной окружности имеет координату Обозначим середины дуг и через и соответственно. Тогда . Найдем координату точки Во-первых откуда При этом лежит на хорде откуда Решая полученную систему, находим Аналогично Заметим, что Тогда ориентированный угол откуда Итого, имеет комплексную координату

Аналогично Тогда

Последнее выражение очевидно вещественное, что и требовалось доказать.

(a) Докажем сначала, что за взвешивание можно найти самую тяжёлую монету. Более точно, мы докажем по индукции по что самую тяжёлую из данных монет можно определить за взвешивание, имея трое весов, одни из которых, возможно, испорчены.

Если то взвесим данные две монеты по очереди на трёх разных весах. Если при одном из взвешиваний весы оказались в равновесии, то эти весы испорчены, значит, мы можем определить более тяжёлую монету по показаниям любых из остальных весов. Если равновесия ни разу не было, то какая-то из монет перевесит хотя бы два раза — она и есть более тяжёлая, так как неверный результат могут давать только одни весы. Это даёт базу индукции.

Пусть теперь Выберем две монеты и двое весов и сравним за первые два взвешивания эти монеты друг с другом на первых и на вторых весах. Возможны два случая:

Оба раза перевешивала одна и та же из двух монет; назовём её монетой а вторую из них — монетой Так как хотя бы одни из двух весов правильные, то монета действительно тяжелее монеты Значит, не самая тяжёлая. Задача сводится к тому, чтобы определить самую тяжёлую из монеты: монеты и монет, не участвовавших в первых двух взвешиваниях. По предположению индукции мы можем сделать это за взвешивания. Вместе с первыми двумя взвешиваниями получаем взвешивания.

Либо одно из первых двух взвешиваний дало равновесия, либо результаты первых двух взвешиваний противоречат друг другу: один раз перевесила одна монета, а другой — другая. Значит, одни из двух использованных весов точно испорчены. Возьмём третьи весы. Тогда они обязательно правильные. Используя из, мы легко можем определить самую тяжёлую монету за взвешивание: сравниваем первую монету со второй, более тяжёлую из них — с третьей, более тяжёлую из них с четвёртой и так далее до последней. Вместе с первыми двумя взвешиваниями получаем (так как ) взвешивание.

Покажем теперь, что менее, чем за взвешивание, заведомо определить самую тяжёлую монету нельзя. Достаточно показать, что её нельзя определить ровно за взвешивания, так как можно добавить произвольные взвешивания и игнорировать их результаты. Предположим противное: имеется алгоритм действий, позволяющий определить самую тяжёлую монету за взвешивания.

Пронумеруем монеты числами Сделаем первые взвешивания согласно алгоритму. Предположим, что в каждом из них перевешивала монета с большим номером. Согласно принципу Дирихле, среди монет с номерами найдётся такая, которая за произведённые взвешиваний "проигрывала"(оказалась более лёгкой) не более одного раза; обозначим номер этой монеты через Конечно же, монета с номером ни разу не "проигрывала". Покажем, что такие результаты взвешиваний возможны. Действительно, такое могло произойти по крайней мере в следующих ситуациях.

(A) Монеты упорядочены по возрастанию масс и все весы (в том числе, испорченные) показывали правильные результаты во всех взвешиваниях.

(Б) Монеты упорядочены по возрастанию масс, за исключением монеты номер которая самая тяжёлая. При этом те весы, на которых монета номер "проиграла испорчены, и в этом взвешивании показали неверный результат, а в остальных взвешиваниях все весы показывали верные результаты.

Рассмотрим два случая:

В последнем, м взвешивании, не участвует монета с номером Предположим, что опять перевесила монета с большим номером. Тогда каждая из ситуаций (А) и (Б) по-прежнему возможна.

В последнем взвешивании участвует монета с номером Предположим, что она перевесила. Тогда, с одной стороны, возможно, что имеет место ситуация (А), и последнее взвешивание выполнялось на испорченных весах. С другой стороны, возможно, что имеет место ситуация (Б), и в последнем взвешивании весы показали правильный результат.

Итак, каким бы ни было одно оставшееся взвешивание, его результат может быть таков, что после него каждая из ситуаций (А) и (Б) будет по-прежнему возможной. Тогда каждая из монет и может быть самой тяжёлой, то есть нам не удалось определить самую тяжёлую монету.

(b) Очевидно, что точно хватит, поскольку мы можем провести алгоритм из предыдущего пункта. В качестве оценки рассмотрим конкретный набор монет с массами Очевидно, что чаша с самой тяжёлой монетой в этом случае всегда будет перевешивать (). В таком случае, можно сделать такую же оценку, как в предыдущем пункте, если понимать слово “проигрывала” как “не была самой тяжёлой” (потому что если монета оказалось на чаше, которая не перевесила, то она точно не самая тяжёлая). То есть чтобы точно определить самую тяжёлую, нам понадобится хотя бы взвешивание.

Обозначим Напомним, что частный случай неравенства Бернулли (при ) можно переписать в виде (при ).

Лемма 1. Для любого натурального п верны неравенства

Доказательство. Правое неравенство сразу следует из упомянутого неравенства Бернулли. Для доказательства левого, применяя то же неравенство, получаем

откуда

Лемма 2. Для любого натурального п верны неравенства

Доказательство. Поскольку достаточно доказать, что или

Применяя лемму получаем

что доказывает левое неравенство. Аналогично, для правого имеем Перейдём к решению задачи. Покажем, что число подходит. Для этого достаточно доказать, что при любом натуральном число с пятёркой в десятичной записи найдётся даже среди чисел Поскольку найдётся натуральное такое, что Покажем, что даже среди -х с конца цифр чисел встретится пятёрка, откуда и будет следовать требуемое. По лемме при каждом имеем это означает, что -я цифра при переходе от к либо не изменяется, либо увеличивается на (при этом переходит в ). С другой стороны, по той же лемме

это означает, что за таких переходов -я цифра обязана хотя бы раз изменить своё значение (на следующее по циклу). Значит, за переходов она примет все возможных значений, в частности, побывает и пятёркой.

Первое решение. Предположим, что многочлен не является монотонным. Тогда найдутся такие что а значит, и то есть не монотонен.

Второе решение. Так как многочлен монотонен, то он обязан иметь нечётную степень, а тогда он принимает все вещественные значения.

Пусть тогда найдутся такие числа и что Так как старший коэффициент многочлена всегда положителен, то этот многочлен возрастает, поэтому

Если старший коэффициент многочлена положителен, то многочлен возрастает; отсюда получаем, что то есть для любых Если же старший коэффициент отрицателен, то, аналогично, откуда для любых

Обозначим через ответ в задаче; положим Докажем сначала, что

После отмечания исходных клеток можно отметить хотя бы одну клетку ; это значит, что либо в столбце, либо в строке этой клетки уже отмечено других клеток - пусть для определённости в строке

Мысленно отметим все клетки строки Ясно, что любую клетку по-прежнему можно отметить. Удалим из клетчатой плоскости строку и сдвинем вместе две получившиеся полуплоскости так, чтобы снова получилась клетчатая плоскость. Теперь мы можем отметить любую клетку этой новой плоскости, отмечая на каждом шагу клетку, в кресте которой уже есть не менее отмеченных клеток (поскольку из этого креста удалена одна клетка строки ). Следовательно, изначально на этой плоскости должно было быть отмечено не менее клеток. Значит, на исходной плоскости сначала должно быть хотя бы отмеченных клеток не из ; отсюда и следует

Поскольку из доказанного неравенства (*) следует, что

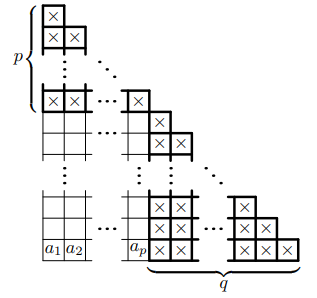
Осталось показать, как отметить клеток так, чтобы затем можно было отметить любую другую клетку плоскости. Покажем по индукции, что подходит пример, показанный на рисунке, состоящий из двух «лесенок» высот и ; нетрудно понять, что в нём как раз клеток. При утверждение очевидно: при одной отмеченной клетке можно отметить любую клетку в её кресте, а затем и любую клетку вообще.

Для перехода индукции заметим, что можно последовательно отметить клетки После этого в строке, в которой они стоят, окажется клеток, и в ней уже можно будет отметить любую клетку. Значит, можно, вычеркнув эту строку, уменьшить значение на и применить предположение индукции в оставшейся плоскости.

Рассмотрим производные изначальных многочленов: Обе производные имеют нули в

Теперь докажем следующую лемму:

Лемма. Имеется множество функций, каждая из которых имеет ноль производной в заданной точке. Тогда, любая новая функция, полученная способом, описанным в задаче, из функций множества, тоже будет иметь корень производной в этой точке.

Доказательство леммы. Пусть новая функция была получена из функций и по одному из способов, упомянутых в условии. По условию леммы имеется такое фиксированное что

 1) Значит, — ноль функции

 2) Значит, — ноль функции

 3) Значит, — ноль функции

 4) Значит, — ноль функции 

Лемма доказана. Вернемся к исходной задаче. По лемме мы получаем, что каждая новая функция на доске будет иметь ноль производной в точке Но рассмотрим функцию, которую мы хотим получить: Заметим, что у ее производной не имеется нуля в точке Значит, по лемме мы не можем получить такую функцию.

Сделаем симметрию относительно биссектрисы угла и инверсию с таким радиусом, чтобы и где штрихом обозначаем образ точки под действием композиции преобразований. Точка является точкой пересечения внешней биссектрисы угла и описанной окружности значит точка переходит в точку пересечения внешней биссектрисы и прямой Точка переходит в основание биссектрисы угла Точка переходит в точку на биссектрисе, которая находится в два раза дальше от чем Из подобия треугольников и и образ можно определить как точку пересечения перпендикуляра к в точке и

Требовалось доказать, что лежат на одной окружности. После инверсии и симметрии остается доказать, что лежат на одной прямой. Заметим, что Достаточно показать, что Тогда треугольники и подобны, и значит прямые и совпадают. Но ясно что

Внутренняя и внешняя биссектрисы делят противоположную сторону в соотношении равном отношению прилежащих сторон. Значит

Это эквивалентно тому, что мы хотели доказать:

Для простого и натурального обозначим через степень, в которой входит в разложение на простые множители. Заметим, что если , то

Предположим противное, обозначим Тогда все простые делители чисел вида не превосходят

Лемма: Пусть при некотором Тогда при всех

Доказательство: Обозначим тогда Заметим, что если В этой сумме все слагаемые, кроме первого, делятся на а первое делится лишь на но не на Значит и делится на но не на

Рассмотрим некоторое простое Ввиду леммы, если при некотором то существует число такое, что при всех натуральных Назовём такое простое число маленьким, все остальные простые числа, меньшие назовём большими. Так как маленьких простых конечное количество, существует натуральное большее любого числа вида где — маленькое.

Пусть теперь — большое простое число, а — такое число, что Тогда из леммы имеем а это означает, что Последний переход верен, так как не кратно

Рассмотрим теперь По доказанному, для любого большого простого Кроме того, поскольку то для любого маленького простого Поскольку все простые делители числа — либо большие, либо маленькие, отсюда следует, что что, очевидно, неверно. Противоречие.

Пусть — первая строка таблицы. Рассмотрим любой набор из чётного количества столбцов и пронумеруем их слева направо: Тогда в таблице есть строка отличающаяся от ровно в столбцах и далее, есть строка отличающаяся от ровно в столбцах и и так далее; наконец, есть строка отличающаяся от ровно в столбцах и (если то ). Итак, строка отличается от ровно в столбцах Значит, строки построенные по различным наборам столбцов, различны. Поскольку количество наборов из чётного числа столбцов равно то и количество строк в таблице не меньше

Зафиксируем точки Пусть точка движется линейно по прямой, проходящей через параллельно Тогда точка так же движется линейно, поскольку Кроме этого, является точкой пересечения серединных перпендикуляров к отрезкам (фиксирован при движении) и (имеет постоянное направление и проходит через середину отрезка которая движется линейно), следовательно движется линейно. Аналогично точка движется линейно.

Рассмотрим треугольник Заметим, что прямая фиксированная, поскольку является серединным перпендикуляром к фиксированному отрезку следовательно высота, проведенная из точки имеет постоянное направление, кроме этого проходит через линейнодвижущуюся точку. То же верно про высоту, проведенную из вершины Наконец, точка пересечения указанных прямых движется линейно. Покажем, что в двух положениях лежит на

Положение 1. Пусть точка такова, что является прямоугольником. Тогда является серединой стороны — Пусть — середина стороны Как известно, является ортоцентром треугольника а значит является ортоцентром треугольника и принадлежит

Положение 2. Пусть совпадает с В этом случае точка определяется как точка пересечения прямой, проходящей через и перпендикулярной и серединного перпендикуляра к точка симметрична относительной прямой

Заметим, что что влечет принадлежность точек и одной окружности.

Наконец, точки и симметричны точке относительно одной из сторон треугольника , следовательно прямая является прямой Штейнера точки относительно треугольника и проходит через ее ортоцентр.

Поставим в каждой красной точке число в каждой синей — а в каждой зеленой — Тогда каждое число на разноцветной дуге равно сумме чисел в ее концах, а каждое число на одноцветной дуге меньше суммы в ее концах. Значит, сумма чисел на дугах не превосходит удвоенной суммы чисел в точках, причем равенство достигается, когда все дуги — разноцветные. Сумма чисел в точках равна поэтому сумма чисел на дугах не больше

Осталось привести пример, когда эта оценка достигается (то есть когда все дуги разноцветны). Расставим сначала по кругу красных точек; затем вставим между соседними красными по точке другого цвета — синих и зеленых. Наконец, вставим оставшиеся зеленых на дуги между красными и синими точками (таких дуг образовалось поэтому их хватит).

Возьмём произвольно и положим . Тогда

Будем далее выбирать

Тогда

Ясно, что последовательность неограниченна, что противоречит условию.

Построим граф, вершины которого соответствуют городам, а ребра — дорогам. Выберем в этом графе самый длинный путь пусть вершины и — концы этого пути. Из условия задачи следует, что в пути не более вершин. Отметим, что концы пути — вершины и не могут быть смежны с вершинами не из (иначе путь можно удлинить). А в случае, когда вершины и смежны и наш путь замыкается в цикл, никакая вершина пути по аналогичным причинам не может быть смежна с вершиной не из

1) Рассмотрим случай, когда в не более вершин. В этом случае рассмотрим любые две вершины и не входящие в путь и концы пути и Среди этих четырех вершин должны быть проведены хотя бы два ребра. Так как ни ни не могут быть смежны с вершинами не из то концы пути и соединены ребром.

Таким образом, путь замыкается в цикл, и тогда ни одна из вершин пути не смежна с вершиной не из Рассмотрим четверку из любых двух вершин и пути и любых двух вершин и не входящих в Так как между этими четырьмя вершинами проведено хотя бы два ребра, то одно из них соединяет и а другое — и Таким образом, в рассматриваемом случае все вершины пути попарно смежны и все вершины не из также попарно смежны. Отсюда очевидно следует утверждение задачи. 2) Рассмотрим случай, когда вне пути лежит ровно одна вершина. Пусть это вершина Если не смежна ни с одной из вершин пути то рассмотрим и любые три вершины пути Поскольку среди этих четырех вершин проведено хотя бы два ребра, то среди любых трех вершин пути проведено хотя бы два ребра. Следовательно, для любой вершины из есть не более одной не смежной с ней вершины пути Поскольку вершин пути нельзя разбить на пары не соединенных ребром, то в должна быть вершина, смежная со всеми остальными вершинами Эта вершина в паре с удовлетворяет утверждению задачи.

Если концы максимального пути и смежны, то, как мы доказали, вершина не смежна ни с одной из вершин пути а этот случай уже разобран.

Остается рассмотреть последний случай, когда концы пути не смежны и вершина смежна хотя бы с одной из вершин пути Рассмотрим вершины и произвольную четвертую вершину (естественно, лежащую на пути ). Так как и попарно не смежны, то смежна хотя бы с двумя вершинами из и Пусть смежна с вершиной пути Одна из соседних с вершин пути не является концом пути. Можно считать, что это первая вершина лежащая на пути из в по ребрам Если смежна с то, пройдя от к по пути далее по ребрам и и затем по пути от к мы обойдем все вершины нашего графа ровно по одному разу, что невозможно по условию. Если же не смежна с то, как мы доказали, эта вершина смежна и с и с Тогда пройдем по ребру далее по пути от к по ребрам и и затем по пути от его конца до вершины, соседней с на пути — получился путь, проходящей по каждой вершине нашего графа ровно один раз, которого по условию не существует. Следовательно, и этот случай не возможен.

Таким образом, мы рассмотрели все случаи и в тех из них, которые возможны, убедились в справедливости утверждения задачи.

Предположим противное: пусть среди четырёх клеток на пересечении любых двух строк и любых двух столбцов есть две клетки одинакового цвета.

Назовём горизонтальной (вертикальной) парой две клетки разного цвета, лежащие в одной строке (одном столбце). Назовём горизонтальным (вертикальным) совпадением две клетки одинакового цвета, лежащие в одной строке (одном столбце). Разделим пары на 6 типов по цветам входящих в них клеток:

Рассмотрим две произвольные строчки. Из предположения следует, что каждые две вертикальных пары с клетками в этих строчках должны иметь общий цвет. Тогда в двух рассматриваемых строчках могут быть вертикальные пары не более, чем трех типов, причем возможны только два принципиально различных случая: все пары содержат один и тот же цвет (скажем, ) или есть пары типов и (или точно так же с другой тройкой цветов). Рассмотрим эти два случая.

Если все пары в наших двух строчках содержат клетку цвета то всего пар не более, чем клеток цвета в обеих строчках, то есть не более Значит, в рассматриваемых двух строчках не менее совпадений.

Пусть есть пары типов и В этом случае все клетки цвета в наших строчках совпадают, таким образом, есть не менее совпадений.

Итак, мы доказали, что в каждой паре строчек не менее вертикальных совпадений. Аналогичный результат верен и для любой пары столбцов. Таким образом, всего в нашем квадрате есть не менее совпадений. Но так как в каждой строке и в каждом столбце по клеток каждого цвета, количество совпадений равно Учитывая, что приходим к противоречию.

Первое решение.

Посмотрим, при каких условиях окружность касается параболы. Пусть есть окружность радиуса с центром в точке а — точка касания окружности и параболы. Проведем касательную Тогда

Проведём через точку прямую, параллельную оси — точка пересечения прямой и оси

Тогда

Получаем, что но , так как — касательная в точке

Значит,

Тогда по теореме Пифагора получаем, что

Теперь рассмотрим случай с двумя окружностями.

Пусть и Тогда

Также знаем, что

Из и получаем, что .

То есть мы поняли, что если есть две окружности радиуса и соответственно, которые касаются параболы и друг друга, то их радиусы отличаются на .

Тогда получается, если то

Второе решение.

Пусть — радиус -й окружности, Тогда уравнение -й окружности имеет вид:

Условие касания означает то, что уравнение имеет один корень, тогда его дискриминат равен нулю, то есть (так как Отсюда

Покажем по индукции, что База уже есть, докажем переход.

Тогда получается, что