Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведена высота
. Точки
и
- середины отрезков
и
. Докажите, что точка
пересечения перпендикуляров, опущенных из точек
и
на прямые
и
соответственно, равноудалена от точек
и
.
Подсказка 1
Пусть перпендикуляры через M и N пересекаются в точке P. Тогда над каким дополнительным построением можно подумать, чтобы сделать MP и NP чем-то хорошим? Не забудьте, что M и N являются серединами отрезков.
Первое решение.
Обозначим точку пересечения перпендикуляров, опущенных из точек и
на прямые
и
соответственно, через
,
а точки, симметричные
и
относительно прямых
и
, через
и
. Тогда прямые
и
—
cерединные перпендикуляры к отрезкам
и
, поэтому достаточно доказать, что четырёхугольник
—
вписанный.
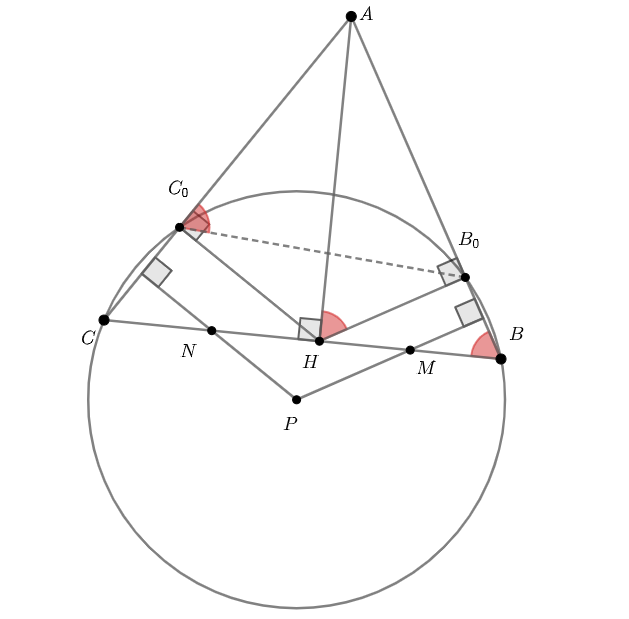
Заметим, что и
содержат средние линии треугольников
и
, параллельные сторонам
и
соответственно. Значит,
Четырёхугольник вписан в окружность, построенную на
как на диаметре, поэтому
по свойству
вписанных углов. При этом
. Значит, четырёхугольник
вписанный.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Обозначим точку пересечения перпендикуляров, опущенных из точек и
на прямые
и
соответственно, через
, а точку
пересечения высот треугольника
— через
.
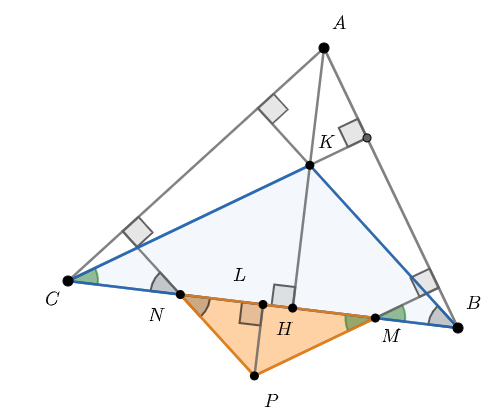
Тогда заметим, что треугольники и
подобны по двум углам. Действительно,
.
Аналогично, выполнено равенство
. Также заметим, что коэффициент подобия этих треугольников равен
, поскольку
.
Опустим из перпендикуляр
на
. Тогда из доказанного подобия следует, что
т. е.
. Следовательно,
а значит,
лежит на серединном перпендикуляре к отрезку
, откуда следует
требуемое.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике высоты
и
пересекаются в точке
. Через точки, в которых окружность радиуса
с центром
пересекает отрезки
и
, проведена прямая
. Аналогично проведены прямые
и
. Докажите, что
точка пересечения высот треугольника, образованного прямыми
, совпадает с центром окружности, вписанной в треугольник
.
Покажем, что биссектрисы треугольника содержат высоты треугольника, образованного прямыми
. Для этого
докажем, что точка пересечения прямых
лежит на биссектрисе угла
, а прямая
перпендикулярна этой
биссектрисе.
_________________________________________________________________________________________________________________________________________________________________________________
Докажем, что прямая перпендикулярна биссектрисе угла
.
Пусть и
- это точки пересечения окружности с центром в
радиуса
с отрезками
и
соответственно. Тогда
треугольник
- равнобедренный с основанием
, поэтому прямая
(она же
) перпендикулярна прямой
, содержащей биссектрису угла
. Поэтому достаточно доказать, что прямая
параллельна биссектрисе угла
.
![]()
Пусть и
— середины дуг
и
окружности
, построенной на
как на диаметре. Из свойств
вписанных углов следует, что
— биссектриса
— биссектриса
. Заметим также, что
- диаметр
окружности
. Значит, отрезки
и
пересекаются в центре окружности
как её диаметры и делятся
точкой пересечения пополам. То есть четырёхугольник
параллелограмм (и даже прямоугольник, поскольку
его углы - вписанные, опирающиеся на диаметры окружности
, то есть прямые). В частности,
, что и
требовалось.
_________________________________________________________________________________________________________________________________________________________________________________
Докажем, что прямые и
пересекаются на биссектрисе угла
.
Пусть прямые и
пересекают отрезки
в точках
и
соответственно, а точку пересечения
и
обозначим
через
. Также обозначим углы
и
треугольника
через
и
соответственно.
![]()
Поскольку и
, то треугольники
и
- равнобедренные с углами, равными
, напротив оснований. Поэтому
. Пусть прямые
и
пересекают
отрезок
в точках
и
соответственно. Тогда треугольник
- равнобедренный с основанием
, значит
. Рассуждая аналогично для треугольника
, получаем, что
. Тогда
получаем
откуда следует, что лежит на окружности, описанной около треугольника
. Аналогично точка
лежит
на окружности, описанной около треугольника
. Таким образом, пять точек
,
лежат на одной
окружности.
Тогда по свойству вписанных углов . Четырёхугольник
вписанный, поскольку
. Значит,
, то есть
. Отсюда следует, что
-
биссектриса угла
. Аналогично
биссектриса угла
. Значит, точка
является центром окружности,
вписанной в треугольник
, в частности, лежит на биссектрисе угла
.
_________________________________________________________________________________________________________________________________________________________________________________
Повторяя рассуждения для двух других биссектрис треугольника , получаем, что точка пересечения биссектрис треугольника
совпадает с точкой пересечения высот треугольника, образованного прямыми
Ошибка.
Попробуйте повторить позже
В треугольнике высоты
и
пересекаются в точке
точка
— середина стороны
а
— точка пересечения
внутренних касательных к окружностям, вписанным в треугольники
и
Докажите, что точки
и
лежат на одной
прямой.
Источники:
Подсказка 1
Пока не совсем понятно, как доказывать вопрос задачи. Углы тут совсем никак не помогут, потому что к ним не подобраться... Давайте попробуем пока в принципе отметить факты на картинке, может быть, что-нибудь в дальнейшем увидим. Например, поймём, где у нас лежат центры вписанных окружностей? Какое дополнительное построение хорошо бы сделать, когда отмечена середина стороны?
Подсказка 2
Верно, центры окружностей лежат на серединном перпендикуляре к сторонам BF и CE, так как треугольники у нас равнобедренные. К тому же если у нас уже есть по средней линии в треугольниках, то давайте проведём ещё по одной параллельно сторонам BF и CE. Значит, у нас уже есть биссектрисы углов B и C, соотношения для которых мы уже можем записать. И попробуем поделить одно соотношение на другое, хуже нам от этого не станет, к тому же у них есть одинаковый отрезок. Давайте немного подумаем. Мы работаем только с отрезками... А как с помощью них можно доказать принадлежность трёх точек одной прямой?
Подсказка 3
Точно, можно доказать, что точка X переводится гомотетией в точку H. Но... Доказывать это через треугольники точно не хочется. Это нужно продлевать серперы до пересечения с линией, параллельной отрезку, проходящего через центры окружностей... Так мы ничего добьёмся. Давайте попробуем доказать утверждение через равенство отношения расстояний от точек X и H до серперов. Одно большое соотношение мы уже получили. Тогда давайте и попробуем выйти через него на отношение расстояний. Давайте взглянем ещё раз внимательно на условие. Чем мы ещё не пользовались?
Подсказка 4
Верно, мы совсем забыли про точку X, а она является центром гомотетии двух окружностей! То есть можем ещё записать отношения с радиусами и двумя отрезками, нужными нам. Остаются только некоторые технические преобразования с отношениями, и победа!
![]()
Первое решение.
Пусть
- середины высот
и
а
- середины отрезков
и
Обозначим окружности, вписанные в
треугольники
через
а их центры - через
и
соответственно. Треугольники
и
-
равнобедренные, поэтому точки
и
лежат на соответствующих высотах
и
этих треугольников. Отрезки
и
являются биссектрисами треугольников
и
поэтому, записывая для них основное свойство биссектрисы, получаем
соотношения
Разделив первое на второе и учитывая равенство
получаем, что
Поскольку
- центр гомотетии, переводящей
в
то
лежит на линии
и верно равенство:
Но
тогда
где обозначает расстояние от точки
до прямой
С другой стороны, по свойству средней линии
и
то есть
и
Значит
и
- прямоугольники, то есть
и
Тогда выполнены
равенства
где последнее равенство выполнено, поскольку и
есть в точности общие перпендикуляры к парам параллельных прямых
и
Собирая все доказанные равенства вместе, получаем, что
откуда следует, что точки
и
лежат на одной прямой.
Второе решение.
Как и в первом решении обозначим окружности, вписанные в треугольники и
через
их центры через
и
соответственно, а середины отрезков
и
— через
и
Пусть также
— точка пересечения внешних касательных к
Заметим, что четвёрка точек — гармоническая, то есть двойное отношение
равно
Спроецируем эту
четвёрку точек на прямую
с центром в точке
Точка
лежит на прямой
поскольку эта прямая является одной из внешних
касательных к
и
поэтому
перейдёт в
Точка
перейдёт в точку
пересечения прямых
и
которая является
серединой
поскольку в треугольнике
отрезок
— средняя линия. Точка
перейдёт в бесконечно удалённую точку
прямой
поскольку
Но при центральной проекции сохраняется двойное отношение четвёрки точек, а четвёрка — гармоническая. Значит,
образом точки
при данной проекции является точка
что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
Пусть — параллелограмм, отличный от прямоугольника, а точка
выбрана внутри него так, что описанные окружности
треугольников
и
имеют общую хорду, перпендикулярную
Докажите, что радиусы данных окружностей
равны.
Источники:
Подсказка 1
Часто в геометрии полезно избавиться от ненужных объектов на картинке. В данном случае это общая хорда окружностей. Как можно переформулировать то что она перпендикулярна AD?
Подсказка 2
Это равносильно тому, что линия центров окружностей параллельна AD!
Подсказка 3
Теперь посмотрите на картинку повнимательнее: между двумя окружностями, которые должны быть равны, есть много общего...
Подсказка 4
Центры обеих окружностей лежат на линии центров, параллельной AD, а также центр первой лежит на...
Подсказка 5
Серединном перпендикуляре к AB! А центр второй - на серединном перпендикуляре к CD. Теперь просто нужно понять, что картинка (AB и центр первой окружности) равна картине (CD и центр второй окружности).
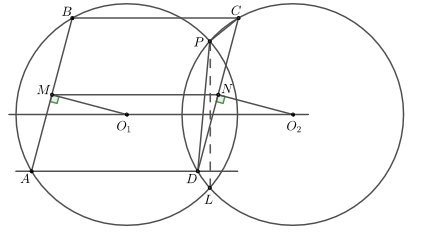
Первое решение.
Заметим, что линия центров перпендикулярна общей хорде данных окружностей, а значит параллельна прямым
и
Пусть
- середина отрезка
- середина отрезка
Тогда
и, поскольку
прямые
и
параллельны. Далее,
и при этом
поэтому
Заключаем, что четырёхугольник
—
параллелограмм по определению, следовательно
Кроме того, поскольку отрезки
и
равны, то по двум катетам
будут равны прямоугольные треугольники
и
следовательно, равны их гипотенузы
и
являющиеся также
радиусами наших окружностей, что и требовалось доказать
Первое решение.
Предположим противное, радиусы окружностей и
описанных около треугольников
и
соответственно,
различны.
При параллельном переносе на отрезок
перейдет в отрезок
окружность
перейдёт в окружность
а прямая
перейдёт в себя. Причём
не может совпадать с
поскольку их радиусы различны. Поэтому
линия центров
совпадающая с прямой
перпендикулярна общей хорде
Таким образом, прямая
параллельна общей хорде окружностей
и
и, следовательно, перпендикулярна прямой
Но тогда параллелограмм
является прямоугольников, что противоречит условию задачи. Следовательно, радиусы окружностей
и
равны.
Ошибка.
Попробуйте повторить позже
В выпуклом 12-угольнике все углы равны. Известно, что длины каких-то десяти его сторон равны 1, а длина ещё одной равна 2. Чему может быть равна площадь этого 12-угольника?
Источники:
Подсказка 1
Пусть длины сторон это 10 единиц, 2 и x. Очень хочется найти x... Попробуем рассмотреть векторы, соответствующие сторонам и поработать с ними.
Подсказка 2
Т.к. мы всё-таки хотим использовать длины сторон, то работать будем не с самими векторами, а с коллинеарными им единичными. Т.к. мы знаем, что они образуют многоугольник, то мы можем записать уравнение на них. А как быть с равными углами? Что можно сказать о взаимно расположении некоторых единичных векторов?
Подсказка 3
Заметим, что каждый угол равен 150. Тогда мы можем сказать, какие стороны многоугольника параллельны. Теперь мы можем записать условия на пары единичных векторов.
Подсказка 4
Знаем, что сумма единичных векторов, где один идёт с коэффициентов 2, а другой - с x равна 0. Также сумма единичных векторов, соответствующим противоположным сторонам тоже равна 0. Как найти x?
Подсказка 5
Чему равна сумма единичных векторов без дополнительных коэффициентов?
Подсказка 6
Их сумма равна 0! Теперь-то мы можем найти x) Осталось лишь найти площадь многоугольника, в котором мы знаем взаимное расположение всех сторон.
Рассмотрим 12-угольник удовлетворяющий условию задачи. У него десять сторон длины 1 и одна сторона длины 2.
Обозначим через
длину оставшейся стороны. Рассмотрим векторы
а также коллинеарные им единичные
векторы
Тогда для некоторых
и
имеет место равенство
Помимо того,
поэтому
Вычитая второе из полученных равенств из первого, получаем
Это возможно лишь в случае, если и
Значит, в исходном 12-угольнике есть пара параллельных сторон длины
2.
В силу равенства всех углов и соответствующих сторон этот 12-угольник имеет ось симметрии:
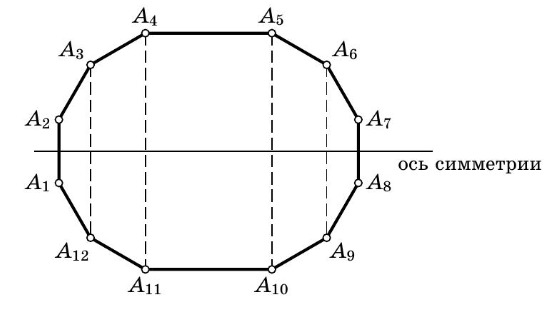
Чтобы найти площадь, разобьём его на 4 трапеции и прямоугольник. Находим
,
поэтому искомая площадь равна
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведена биссектриса
На продолжении отрезка
за точку
выбрана точка
так, что
. Описанные окружности треугольников
и
пересекают отрезки
и
в точках
и
соответственно.
Докажите, что прямые
и
параллельны.
Источники:
Подсказка 1
Такс, нам необходимо доказать параллельность прямых... Мы можем либо доказать, что AQ/AB=AP/AC, либо как-то посчитать уголочки. Мы знаем, что биссектриса делит сторону в хорошем отношении. Mожет, тогда подумаем по поводу отрезков?
Подсказка 2
Из свойства биссектрисы мы знаем, что AB/AC=BL/LC. Также на картинке можно заметить много секущих, поэтому логично попробовать посчитать их. Например: BL*BC=BQ*BC₁, где C₁- точка пересечения прямой BA с описанной окружностью треугольника △CLK. Если BQ как-то связана с пропорцией, которую нам надо доказать, то BC₁- не очень. Что мы можем сказать про отрезок AC₁?
Подсказка 3
Т.к. AL=AK и уголочки ∠KAC₁ и ∠LAC равны, то из симметрии AC₁=AC. Тогда: BL*BC=BQ*BC₁=BQ*(BA+AC). Аналогично можно получить, что CL*CB=CP*(AC+AB) ⇒ BL/CL=BQ/CP. Что это нам дает?
Подсказка 4
Т.к. BQ=AB-AQ и CP=AC-AP, а BL/LC=AB/AC ⇒ AB/AC=(AB-AQ)/(AC-AP). Докажите, что из этого следует равенство AB/AC=AQ/AP, и радуйтесь жизни!
Рассмотрим отрезок он является общей хордой окружностей, описанных около треугольников
и
Точка
— середина
поэтому она лежит на линии центров
этих окружностей. Продлим
и
до пересечения с окружностями в точках
и
соответственно. В силу симметрии получившейся конструкции относительно прямой
отрезки
и
равны отрезкам
и
соответственно.
![]()
Введём следующие обозначения:
По свойству
секущей
Аналогично, для секущих и
получаем
Разделив одно равенство на другое, получим
По свойству биссектрисы треугольника
получаем
Отсюда
Раскрывая скобки и приводя подобные члены, получаем
Откуда, по обратной теореме о пропорциональных отрезках, следует, что
Ошибка.
Попробуйте повторить позже
Дана равнобокая трапеция, сумма боковых сторон которой равна большему основанию. Докажите, что острый угол между диагоналями не
больше чем
Источники:
Трапеция вписана в окружность. Ее боковая сторона вдвое меньше основания и, значит, не длиннее радиуса окружности. Поэтому
боковые стороны стягивают дуги не больше чем
А угол между диагоналями равен полусумме этих дуг.
Ошибка.
Попробуйте повторить позже
В правильном пятиугольнике отмечена точка
— середина
Серединный перпендикуляр к
пересекает
в точке
Докажите, что прямая
перпендикулярна прямой
Источники:
Первое решение. Угол правильного пятиугольника равен тогда
Таким образом, содержит биссектрису треугольника
и, следовательно, пересекает серединный перпендикуляр к стороне
в точке, лежащей на описанной около этого треугольника окружности. Но
прямой, значит, и
прямой, как опирающийся на ту
же дугу.
Второе решение.
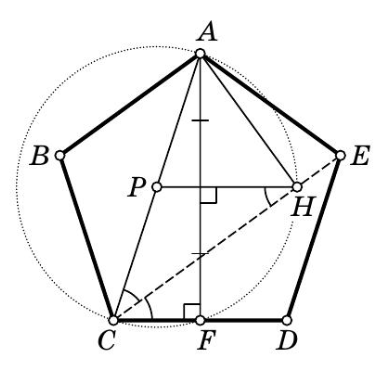
Аналогично первому решению Так как
то по теореме Фалеса
где
— точка
пересечения серединного перпендикуляра к
с диагональю
а углы
и
равны как внутренние накрест
лежащие:
Следовательно, треугольник
равнобедренный и
Окончательно получаем,
что
и треугольник
прямоугольный, так как его медиана равна половине стороны, к которой она
проведена.
Ошибка.
Попробуйте повторить позже
Дан правильный треугольник На стороне
отмечена точка
на стороне
— точки
и
(
лежит на отрезке
)
так, что
Найдите
Источники:
Решение 1.
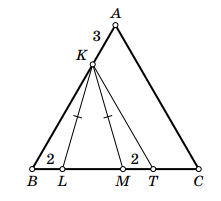
Отметим на продолжении отрезка за точку
такую точку
что
Углы
и
равны, так как они смежные
с равными углами равнобедренного треугольника
Значит, треугольники
и
равны по двум сторонам и углу между
ними. Тогда равны их соответствующие углы:
В треугольнике два угла по
поэтому он равносторонний, и
Так как треугольник
тоже равносторонний и
то
(и точка лежит именно на стороне
а не на ее продолжении). Тогда
Решение 2.
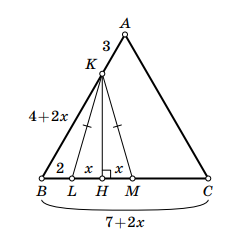
Проведем высоту равнобедренного треугольника
Она также является его медианой, поэтому
Обозначим
Треугольник
— прямоугольный с углом
равным
а значит, его гипотенуза
в
раза больше его
катета
Так как
то
а тогда
Треугольник равносторонний, поэтому
А значит,
Ошибка.
Попробуйте повторить позже
Точка — середина стороны
треугольника
Окружность
проходит через точку
касается прямой
в точке
и
пересекает сторону
в точке
а сторону
— в точке
Пусть
и
— середины отрезков
и
соответственно.
Докажите, что окружность, описанная около треугольника
касается
Источники:
Подсказка 1
У нас есть с вами сразу три середины каких-то отрезков. Понятно, что можно тогда где-то найти средние линии и параллельности) Что из этого получится?
Подсказка 2
Из этого можем получить, что ∠XMY = ∠A. Теперь подумайте: что значит, что окружности будут касаться? Скорее всего, вы понимаете даже, где. Какое условие там будет выполнено?
Подсказка 3
Хочется, чтобы они касались в точке M, то есть нужно, чтобы описанная около XMY окружность касалась BC в точке M. То есть, ∠YMC = ∠YXM. А мы знаем, что ∠YMC = ∠ABC. По факту что нам достаточно теперь доказать?
Подсказка 4
Из знания уже одного угла нам достаточно доказать, что XMY подобен треугольнику ABC! Для этого попробуйте использовать то, что это средние линии, а нужные удвоенные отрезки можно выразить с помощью теорем о касательной и секущей :)
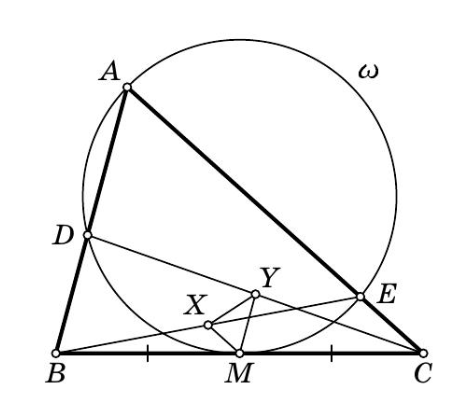
Заметим, что и
— средние линии треугольников
и
поэтому
и
Тогда
По свойству касательной и секущей к окружности имеем откуда
Аналогично получаем
Деля одно на другое и пользуясь тем, что находим
Получаем, что треугольники и
подобны по углу и отношению прилежащих сторон.
Тогда Получается, что в описанной окружности треугольника
угол, опирающийся на хорду
равен углу между хордой
и прямой
Это значит, что прямая
касается окружности, описанной вокруг треугольника
Следовательно, рассматриваемые окружности касаются.
Ошибка.
Попробуйте повторить позже
Точка — центр описанной окружности треугольника
Серединный перпендикуляр к
пересекает
и
в точках
и
Прямая
пересекает прямую
в точке
— середина
Описанная окружность треугольника
пересекает
описанную окружность треугольника
в точке
отличной от
Докажите, что прямая
касается описанной окружности
треугольника
Источники:
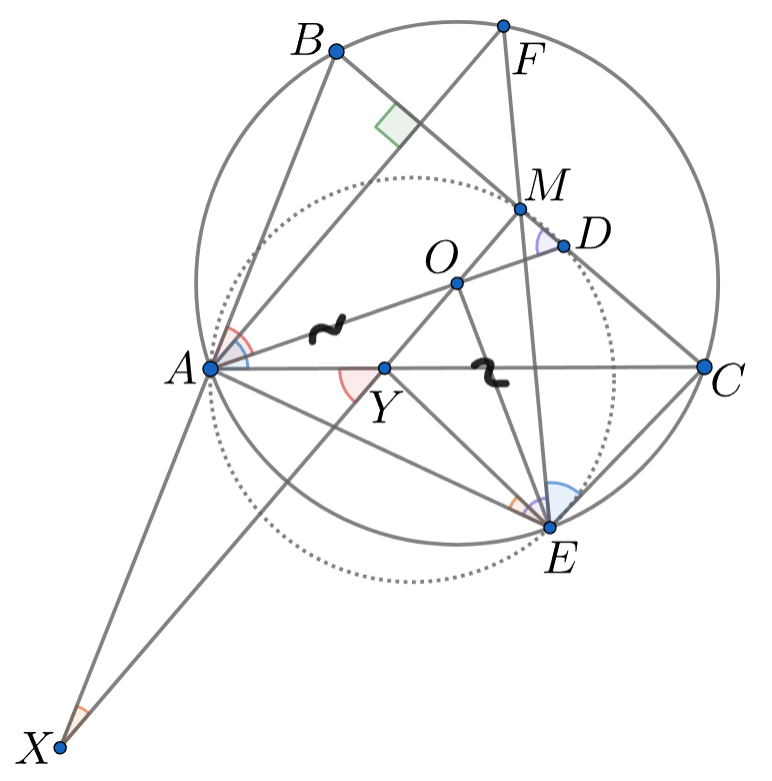
Заметим, что касается описанной окружности треугольника
так как
Пусть — точка на окружности, описанной около
такая что
Ясно, что
Получаем, что и
лежат на одной прямой. Кроме того,
что значит, что
и
лежат на одной окружности. Далее,
т. е. лежит на описанной окружности треугольника
Тогда
— касательная, так как
и
— касательная к
окружности
Ошибка.
Попробуйте повторить позже
На стороне треугольника
взяли такую точку
что угол
равен углу
Чему равно наименьшее возможное
расстояние между центрами окружностей, описанных около треугольников
и
если
Источники:
Пусть и
— центры окружностей, описанных около треугольников
и
соответственно, а
— середина стороны
Треугольники
и
подобны, так как у них угол
общий, а два других угла равны по условию. Поэтому оставшиеся углы этих
треугольников
и
также равны. Это означает, что описанная окружность треугольника
касается прямой
а радиус
перпендикулярен касательной
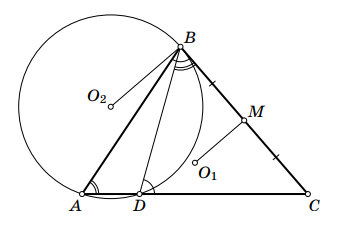
Кроме того, лежит на серединном перпендикуляре к стороне
Поэтому отрезок
длины
является ортогональной проекцией
отрезка
на прямую
Но проекция не длиннее отрезка, поэтому
причём равенство достигается, когда угол
равен
так как в этом случае
— середина стороны
а
— середина стороны
— средняя линия треугольника
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике (
) провели высоту
Точка
симметрична точке
относительно прямой,
соединяющей середины сторон
и
Докажите, что прямая
содержит центр описанной окружности треугольника
Первое решение.
Воспользуемся теоремой о прямой Штейнера: точки, симметричные произвольной точке описанной окружности треугольника
относительно его сторон, лежат на одной прямой, проходящей через ортоцентр (точку пересечения высот) треугольника
Несложно заметить, что точка лежит на окружности, проходящей через середины сторон треугольника
(это окружность
девяти точек треугольника
).
По условию точка симметрична точке
относительно средней линии, параллельной стороне
Заметим, что точка
симметрична точке
относительно средней линии, параллельной стороне
Получается, что прямая
— это прямая Штейнера
точки
относительно серединного треугольника (треугольника, образованного серединами сторон треугольника
). Тогда на этой
прямой лежит ортоцентр серединного треугольника, который и является центром описанной окружности треугольника
______________________________________________________________________________________________________________________________________________________
Второе решение.
Отметим середины и
сторон
и
соответственно. Заметим, что треугольник
— прямоугольный, а точка
—
середина его гипотенузы
Значит,
Поскольку точки
и
симметричны относительно прямой
то
Следовательно, точки
лежат на одной окружности с центром в точке
Отсюда
так как эти
углы опираются на одну дугу
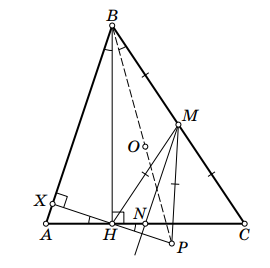
Обозначим точку пересечения прямых и
через
Заметим, что
из-за симметрии точек
и
относительно
прямой
Кроме того,
как средняя линия треугольника
Таким образом,
Отсюда следует, что
С другой стороны, заметим, что если точка — центр описанной окружности треугольника
то
как
центральный угол, и из суммы углов равнобедренного треугольника
получаем, что
. Имеем
а значит, точки
и
действительно лежат на одной прямой.
Ошибка.
Попробуйте повторить позже
Дана трапеция с основаниями
и
Перпендикуляр, опущенный из точки
на сторону
проходит через середину
диагонали
а перпендикуляр, опущенный из точки
на сторону
проходит через середину диагонали
Докажите, что
трапеция равнобокая.
Источники:
По замечательному свойству трапеции точка пересечения продолжений боковых сторон точка пересечения диагоналей
и середина
основания
точка
лежат на одной прямой. Пусть
— середины диагоналей
и
Тогда
т. е.
— тоже
трапеция, и по её замечательному свойству точка
точка пересечения её диагоналей
и точка
лежат на одной прямой.
Следовательно, точки
и
лежат на одной прямой.
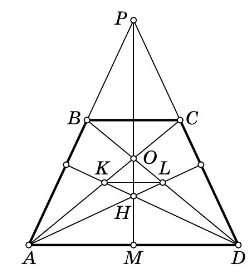
Для завершения доказательства рассмотрим треугольник в нём точка
— точка пересечения высот к сторонам
и
следовательно, медиана
проходит через его ортоцентр и является высотой. Таким образом, треугольник
— равнобедренный,
откуда немедленно следует, что и трапеция
— равнобокая.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике проведены высоты
и
, точка
— центр его описанной окружности. Докажите, что
расстояние от точки
до прямой
равно расстоянию от точки
до прямой
.
![]()
Введём обозначения, — углы треугольника при вершинах
соответственно.
По свойству ортоцентра и тому, что треугольник прямоугольный получаем
Значит, т.к. треугольник прямоугольный
А из прямоугольного треугольника получаем, что
Подставив эти равенства одно в другое, в итоге получим, что
Теперь из того, что — центр описанной окружности и равнобедренного треугольника
в котором
как радиусы,
выражаем
Т.к. треугольники и
прямоугольные, то
Видно, что
Что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
Биссектриса угла пересекает описанную окружность
треугольника
в точках
и
. Точка
— середина отрезка
.
На дуге
окружности
выбрана точка
так, что
. Прямые
и
пересекают прямую
в точках
и
соответственно. Докажите, что
.
Источники:
Пусть прямая пересекает
и
в точках
и
соответственно. Также обозначим
и
(указанные углы равны, как опирающиеся на одну дугу и углы при параллельных прямых). Последовательно применяя теорему синусов
для треугольников ,
и
, получим:
Аналогично, применяя теорему синусов для треугольников ,
и
, получим:
То есть
Ошибка.
Попробуйте повторить позже
На сторонах выпуклого шестиугольника во внешнюю сторону построены правильные треугольники
и
Оказалось, что треугольник
правильный. Докажите, что треугольник
также правильный.
Источники:
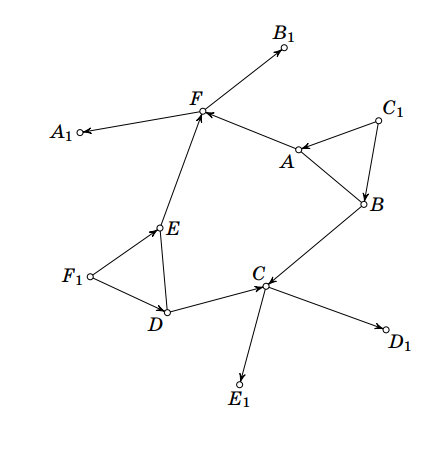
По условию треугольники и
являются правильными. Значит, при повороте на
против часовой стрелки
векторы
и
перейдут в векторы, равные
и
соответственно. Имеем
и
Отсюда получаем, что вектор
при таком повороте перейдёт в вектор, равный
Также по условию треугольники и
являются правильными. Значит, при повороте на
против часовой
стрелки векторы
и
перейдут в векторы, равные
и
соответственно. Отсюда получаем, что векторы
и
при таком повороте перейдут в векторы, равные
и
соответственно. Следовательно, при повороте на
против часовой стрелки или, что то же, при повороте на
по часовой стрелке,
вектор
перейдёт в вектор, равный
Наконец, по условию треугольник является правильным. Значит, при повороте на
по часовой стрелке вектор
перейдёт
в вектор, равный
Отсюда получаем, что вектор
при таком повороте перейдёт в вектор, равный
Следовательно, треугольник
также являетсяя правильным.
Ошибка.
Попробуйте повторить позже
Дан выпуклый четырёхугольник с попарно непараллельными сторонами. На стороне
выбирается произвольная точка
отличная от
и
Описанные окружности треугольников
и
вторично пересекаются в точке
Докажите, что прямая
проходит через фиксированную точку, не зависящую от выбора точки
Источники:
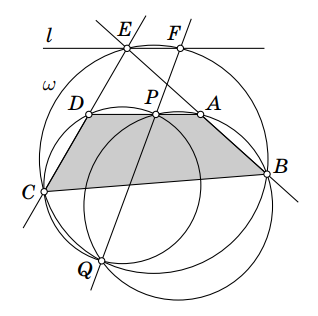
Обозначим через пересечение прямых
и
Рассмотрим случай, в котором точка
лежит на луче
за точкой
Четырехугольники
и
— вписанные, значит,
а
Сумма углов треугольника
равна
Следовательно, четырехугольник вписан в окружность
— описанную окружность треугольника
Обозначим через вторую точку пересечения прямой
с
Четырехугольник
— вписанный. Значит,
Отсюда следует, что прямые
и
параллельны.
Пусть — прямая, проходящая через точку
параллельно
Тогда прямая
независимо от выбора точки
проходит через
вторую точку пересечения окружности
и прямой
Случай, когда точка
лежит с другой стороны, разбирается
аналогично.
Ошибка.
Попробуйте повторить позже
Точка — центр описанной окружности треугольника
— его высота. Точка
— основание перпендикуляра, опущенного из
на прямую
Докажите, что прямая
проходит через середину отрезка
Источники:
Первое решение. Снова будем считать описанную окружность треугольника единичной с центром в
Поскольку
—
основание перпендикуляра, опущенного из
на диаметр
получаем
Точка
является
проекцией точки
на прямую
откуда
Пусть
— середина отрезка
Тогда
Осталось
показать, что
Второе решение.
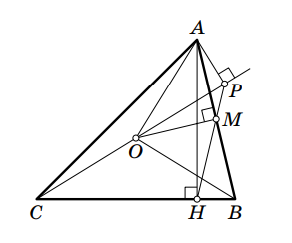
Пусть — середина отрезка
Рассмотрим точки
и
Поскольку
точки
и
лежат
на одной окружности. Значит,
Рассмотрим точки
и
Они также лежат на одной окружности, так
как
Следовательно,
Помимо того, Получаем:
Значит,
точки
и
лежат на одной прямой.
Ошибка.
Попробуйте повторить позже
На сторонах выпуклого шестиугольника во внешнюю сторону построены равносторонние треугольники
и
Оказалось, что треугольник
— равносторонний. Докажите, что треугольник
также равносторонний.
Расположив шестиугольник на комплексной плоскости в правильной ориентации, и введя соответствующие комплексные координаты,
получаем Условие правильности положительно ориентированного
треугольника
равносильно тому, что
(это условие означает, что вектор
получается из вектора
поворотом на
против часовой стрелки). То есть
Используя равенство после раскрытия скобок и приведения подобных получаем
Аналогично условие правильности треугольника равносильно тому, что
Мы знаем, что Воспользовавшись тем, что
получаем требуемое после раскрытия
скобок.



