Стереометрия на ММО —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Стереометрия на ММО

Тема ММО (Московская математическая олимпиада)

Стереометрия на ММО

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ммо (московская математическая олимпиада)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#85489

В тетраэдре $ABCD$ скрещивающиеся рёбра попарно равны. Через середину отрезка $AH A$ , где $H A$ - точка пересечения высот грани $BCD$ , провели прямую $hA$ перпендикулярно плоскости $BCD$ . Аналогичным образом определили точки $HB, HC$ , $HD$ и построили прямые $hB,hC,hD$ соответственно для трёх других граней тетраэдра. Докажите, что прямые $hA,hB,hC,hD$ пересекаются в одной точке.

Показать доказательство

Проведём через пару скрещивающихся рёбер тетраэдра $ABCD$ две параллельные плоскости. Так же поступим для двух других пар скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани — прямоугольники, и параллелепипед прямоугольный. Пусть $O$ — его центр, являющийся также центром описанной сферы тетраэдра $ABCD.$ Пусть также $′ ′ ′ ′ A ,B ,C ,D$ — точки, симметричные $A,B,C,D$ соответственно относительно точки $O.$ Докажем, что все построенные прямые проходят через точку $O.$

$PIC$

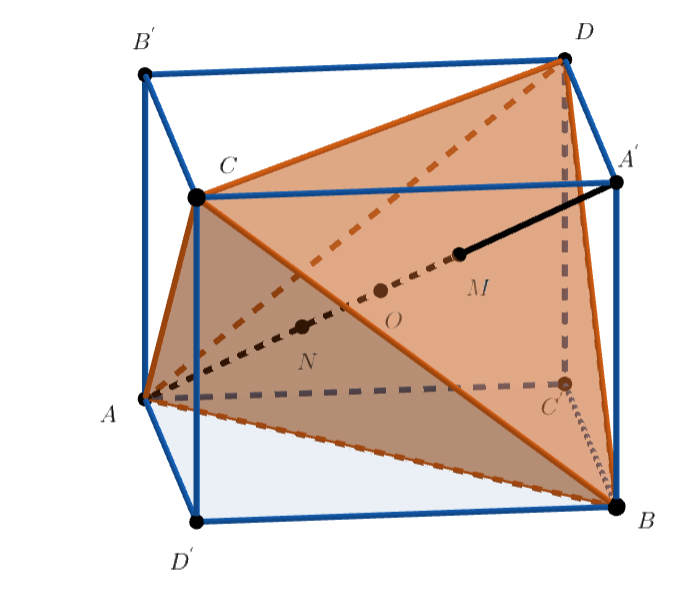
Пусть $M$ — центр масс треугольника $BCD$ . Тогда

−−−′→ 1−−′→ −−→′ −−→′ A M = 3(A B +A C +A D )

То есть точка $M$ лежит на диагонали $′ AA$ и делит её в отношении $2:1$ , считая от вершины $A.$ Аналогично центр масс $N$ треугольника $′ ′ ′ B CD$ лежит на этой диагонали и делит её в отношении $1:2$ , считая от вершины $A.$ Точка $O$ — середина отрезка $NM,$ поэтому $AO :OM = 3:1.$

$PIC$

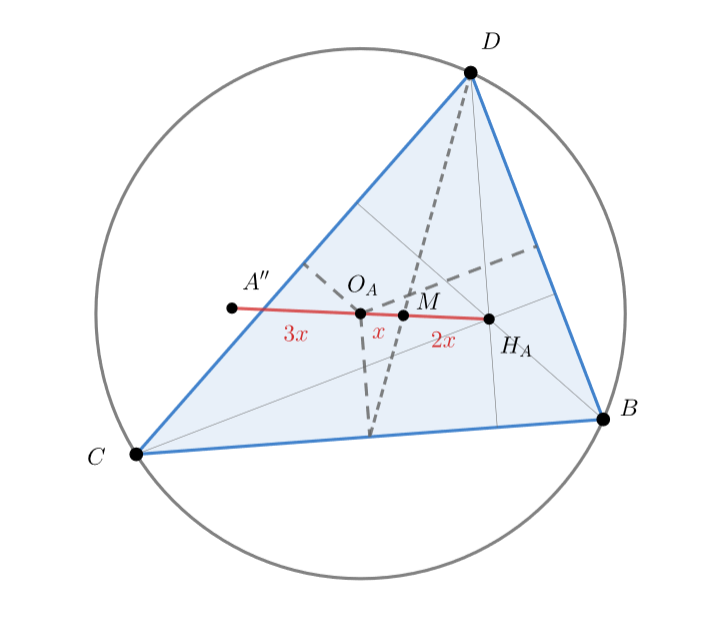
Рассмотрим проекцию на плоскость $BCD :$ $A ′′$ — проекция точки $A$ , $OA$ — проекция центра $O.$ Точка $O$ совпадает с центром описанной сферы тетраэдра $ABCD,$ поэтому $OA$ — центр описанной окружности треугольника $BCD.$

Тогда прямая $AA ′$ проецируется в прямую Эйлера $OAM$ треугольника $BCD.$ Пусть $OAM = x.$ Тогда $OAA ′′= 3x$ ( $O$ делит отрезок $AM$ в отношении $3:1$ , это отношение сохраняется при проецировании). Кроме того, $OA,M, HA$ лежат на одной прямой и $OAM :MHA = 1:2$ (прямая Эйлера), отсюда $MHA =2x.$ Следовательно, $OAA ′′ = OAHA$ , а прямая $OOA$ , перпендикулярная плоскости $BCD$ , делит отрезок $AHA$ пополам, а значит, совпадает с прямой $hA$ . Итак, все построенные прямые проходят через точку $O$ .

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#67674

Середины всех высот некоторого тетраэдра лежат на его вписанной сфере. Верно ли, что тетраэдр правильный?

Источники: ММО-2023, 11.5 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Попробуем разобраться в этом тетраэдре. Мы знаем, что середина каждой высоты лежит на вписанной сфере. Какое неравенство, связанное с высотой и радиусом вписанной сферы, мы можем получить?

Подсказка 2

Если Hi- длина произвольной высоты тетраэдра, то Hi/2<=2r, где r- радиус вписанной сферы. Это можно увидеть, если провести плоскость, параллельную плоскости основания высоты и касающуюся вписанной сферы. Что же может дать нам это неравенство? Полезно было бы вспомнить о том, что Hi и r связаны объёмом тетраэдра...

Подсказка 3

Обозначим за Si- площадь произвольной боковой грани. Тогда: 3*V=Hi*Si=r*(S1+S2+S3+S4), где V- объем тетраэдра. Попробуйте теперь воспользоваться неравенством Hi/2<=2r...

Подсказка 4

Подставив неравенство в равенство, мы получим, что: r*(S1+S2+S3+S4)<=4*r*Si. Сократим обе части на 4*r: (S1+S2+S3+S4)/4<=Si. Получается, что произвольно выбранная площадь не меньше среднего арифметического всех площадей. Это как-то странно...

Подсказка 5

Давайте предположим, что Si не больше всех оставшихся площадей. Тогда: Si=(Si+Si+Si+Si)/4<=(S1+S2+S3+S4)/4<=Si. Это означает, что все Si равны между собой. Тогда и все высоты равны между собой. Во что превращается неравенство Hi/2<=2r?

Подсказка 6

Положим, что S1=S2=S3=S4=S, а H1=H2=H3=H4=H. Т.к. H*S=r*(S1+S2+S3+S4) получаем, что H=4r. Но тогда высоты обязаны содержать центр вписанной окружности и точку касания с гранью. Может как-то выразить длины ребер через высоты...

Подсказка 7

Для определенности проведем высоту AH и будем искать ребро AB. По теореме о касательной и секущей получаю, что BH^2=H*H/2. Теперь осталось воспользоваться теоремой Пифагора для треугольника ABH и увидеть, как AB выражается через H.

Показать ответ и решение

$PIC$

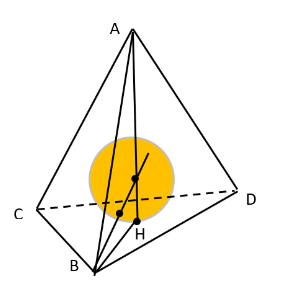
Рассмотрим тетраэдр $ABCD,$ удовлетворяющий условию задачи. Заметим, что по условию для любой высоты $hi$ данного тетраэдра справедливо неравенство $hi2-≤2r,$ где $r$ — радиус вписанной сферы, то есть $hi ≤ 4r,i=1,2,3,4.$

Пусть $Si$ — площадь грани, на которую опущена высота $hi.$ Докажем, что $S1 = S2 =$ $=S3 =S4.$ Предположим противное. Выберем грань минимальной площади (если таких граней несколько, то берём любую из них). Без нарушения общности можно считать, что её площадь равна $S1$ (иначе можно ввести переобозначения). Так как не все $Si$ равны между собой и $S1$ - наименьшая из них, то

S1+-S2+S3-+S4->S1 4

Выразим объём тетраэдра двумя способами:

V = 1h S = 1r(S + S + S +S )> 1r⋅4S 3 1 1 3 1 2 3 4 3 1

Отсюда $h1 > 4r,$ что противоречит неравенству $h1 ≤4r$

Итак, все $Si$ равны, поэтому все $hi$ равны, так как $3V hi = Si .$ Обозначим за $h$ длину этих равных высот. Из приведённого выше соотношения для объёма получаем $h= 4r,$ то есть неравенство обращается в равенство. Но это возможно только в случае, если высота содержит центр сферы и точку касания с гранью (и так для каждой высоты).

Пусть $H$ - основание высоты тетраэдра, опущенной из точки $A.$ Тогда $H$ совпадает с точкой касания сферы и грани $BCD$ Пусть $BH = a,$ тогда по теореме о касательной и секущей $2 h a = 2 ⋅h.$ По теореме Пифагора из прямоугольного треугольника $ABH$ получаем

h2 3h2 AB2 =AH2 + BH2 =h2 +a2 = h2+ 2-=-2-

Аналогично получаем такое же выражение для остальных рёбер тетраэдра, следовательно, они равны между собой, то есть тетраэдр правильный.

Ответ: верно

Ошибка.
Попробуйте повторить позже

Задача 3#72972

Звездолёт находится в полупространстве на расстоянии $a$ от его границы. Экипаж знает об этом, но не представляет, в каком направлении двигаться, чтобы достигнуть граничной плоскости. Звездолёт может лететь в пространстве по любой траектории, измеряя длину пройденного пути, и имеет датчик, подающий сигнал, когда граница достигнута. Может ли звездолёт гарантированно достигнуть границы, преодолев путь длиной не более $14a?$

Источники: ММО-2022, 11.4 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

В условии сказано, что пройдя расстояние, равное a, в определенную сторону, звездолет покинет полупространство. Каким образом мы можем описать все варианты той точки, где кончается полупространство?

Подсказка 2

Мы можем сказать, что если звездолет находится в какой-нибудь точке О, то на сфере с центром в точке O и радиусом a гарантированно найдется точка , которая уже не будет являться частью полупространства. Подумайте, как данная сфера может помочь в выборе траектории. Может быть, есть какая-то фигура, которую удобно будет описать около сферы?

Подсказка 3

Рассмотрите правильный октаэдр, описанный около данной сферы. Если мы докажем, что путь из центра октаэдра по всем вершинам без повторений меньше 14a и хотя бы одна вершина гарантировано не лежит в полупространстве, то мы решим задачу. Сначала подумайте, как можно сделать второе.

Подсказка 4

Воспользуемся методом от противного. Подумайте, где возникает противоречие, если мы скажем, что все вершины октаэдра лежат в данном полупространстве.

Подсказка 5

Теперь нужно найти длину пути от О и по всем вершинам. Давайте назовем наш октаэдр A₁A₂A₃A₄A₅A₆, тогда не трудно найти кратчайший маршрут обхода: O -> A₁ -> A₂ -> A₃ -> A₄ -> A₅ -> A₆. Как можно найти длину данного пути?

Подсказка 6

Для начала нужно найти длину отрезка OA₁, так как из него легко можно выразить длину ребра октаэдра. Мы знаем, что длина высоты, опущенной из точки О на грань октаэдра равна a, Тогда как мы можем найти длину OA₁?

Подсказка 7

Давайте рассмотрим пирамиду OA₁A₂A₃, найдем ее объем двумя разными способами, как 1/6 куба с ребром OA₁ и через длину высоты и площадь A₁A₂A₃. Из равенства двух данных выражений легко можно выразить OA₁. Для окончательного решения останется только найти длину ребра и доказать, что предложенный нами маршрут меньше 14a.

Показать ответ и решение

$PIC$

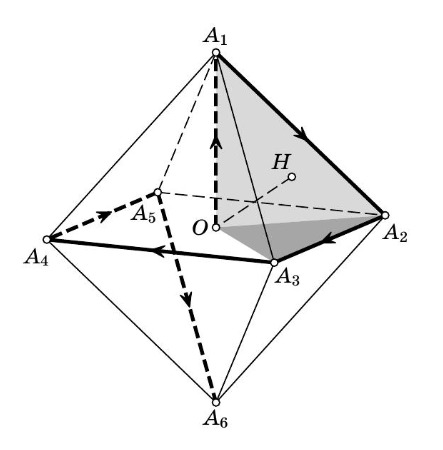
Пусть корабль находится в некоторой точке $O.$ Рассмотрим правильный октаэдр $A1A2A3A4A5A6,$ описанный возле шара радиуса $a$ с центром в точке $O.$ Докажем, что путь $O → A1 → A2 → A3 → A4 → A5 → A6$ заведомо позволит достигнуть граничной плоскости.

Предположим противное. Тогда вершины октаэдра, а значит, и сам октаэдр (выпуклая оболочка его вершин) лежат строго внутри полупространства. Поэтому вписанный шар октаэдра, радиус которого равен $a,$ тоже лежит строго внутри полупространства. Получаем противоречие, так как по условию расстояние до граничной плоскости полупространства равно $a.$

Покажем теперь, что длина пути $O→ A1 → A2 → A3 → A4 →$ $→ A5 → A6$ меньше $14a.$ Пусть $OA1 =OA2 = OA3 = x,OH$ — высота пирамиды $OA1A2A3.$ Запишем ее объём двумя способами:

√- V = 1x3 = 1⋅OH ⋅S = 1⋅a⋅√3 ⋅ (x-2)2 6 3 A1A2A3 3 4

Отсюда получаем, что $√- x= a 3,$ а длина ребра октаэдра равна $√- a 6.$ Поэтому длина пути равна $√ - √- ( 3+5 6)a< 14a,$ так как $√ - 2< 43∕30.$

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 4#42963

Найдите все прямые в пространстве, проходящие через данную точку $M$ на данном расстоянии $d$ от данной прямой $AB$ .

Источники: ММО-1947, 9-10.5, (см. mccme.ru)

Подсказки к задаче

Подсказка 1!

Давайте попробуем сначала разобраться с простым случаем, чтобы нам было понятнее, что происходит. Есть точка в пространстве. И прямая в пространстве. И если расстояние от самой точки до прямой уже d, то какой был бы ответ?

Подсказка 2!

Верно, это была бы плоскость через точку, параллельная АВ. Так, а если расстояние от точки до плоскости меньше d?

Подсказка 3!

Хорошо, с этим тоже разобрались. Такого гмт бы не существовало. Давайте теперь посмотрим на сложный случай. Чтобы расстояние было равно d, попробуем построить одну такую прямую. Возьмем вокруг AB "оболочку" ширины d. получится такой цилиндр радиуса d. И вам нужна прямая, которая будет проходить через точку m, а еще касаться такого цилиндра(осознайте, почему?). Осталось немного, разобраться, как построить такое гмт!

Показать ответ и решение

Если точка сама находится на расстоянии $d$ от $AB$ , то подойдёт вся плоскость $α∥AB$ , $M ∈α$ (то есть любая прямая $ℓ: ℓ∈ α,M ∈ℓ$ . Если расстояние $ρ(M,AB)< d$ , то таких прямых нет. Иначе это прямая, которая касается цилиндра с осью $AB$ и проходит через $M$ . Чтобы задать такие прямые, построим касательную плоскость к цилиндру, которая содержит $M$ — в силу симметрии их будет две $β1,β2$ . В итоге нам подойдут все $ℓ∈ β1∪β2,M ∈ℓ$ . Нетрудно видеть, что в случае равенства $ρ(M,AB )= d$ плоскости просто совпадают.

Ответ:

Если $ρ(M,AB )≥d$ , то это все $ℓ: ℓ∈β ∪ β,M ∈ ℓ 1 2$ , где $β i$ — касательные плоскости к цилиндру с осью $AB$ и радиусом $d$ , при этом $M ∈ β1∩β2$ .

Курсы

Всё необходимое для достижения цели

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Предыдущий раздел

Следующий раздел