Комбинаторика и теория чисел на Физтехе —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Комбинаторика и теория чисел на Физтехе

Тема Физтех

Комбинаторика и теория чисел на Физтехе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела физтех

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#80772

Для целых чисел $a$ , $b$ , $c$ известно, что $a< b$ , $b− a$ не делится на 3, $(a− c)(b− c)$ равно квадрату простого числа, наконец, $2 a + b= 1000$ . Найдите все такие тройки $(a,b,c)$ .

Источники: Физтех - 2024, 11.6 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Во-первых, давайте поймем, что если (a - c)(b - c) = p^2, то у нас есть не так много возможных случаев, так как a - c и b - c - это делители p^2, а их у нас всего +-1,+-p,+-p^2. Значит, у нас всего 6 вариантов. А как можно, используя условие, еще сократить количество вариантов, которые надо перебрать?

Подсказка 2

Можно, используя условие a < b, сказать, что a - c < b - c => у нас есть два варианта: первая скобка равна 1, вторая p^2 или первая равна -p^2, а вторая -1. Хорошо, у нас получилась совокупность систем. Как нам её решить?

Подсказка 3

Во-первых, надо избавиться от c (ни к селу, ни к городу это с) и получить, что a - b = p^2 - 1. При этом, a - b (то есть, p^2 - 1) не кратно 3. Но любой ненулевой остаток квадрата числа дает 1 по модулю 3. Значит, p кратно 3. Что тогда можно сказать про a, b, c? Как меняется наша система?

Подсказка 4

Это значит, что p = 3, а значит, a - b = 8; a^2 + b = 1000. Остаётся решить квадратное уравнение на а, которое получается из этой системы, и найти все с, которые подходят.

Показать ответ и решение

Второе условие можно записать как

2 (a − c)(b− c)=p , где p — простое число

По условию $a< b,$ это значит, что $a − c< b− c.$ Тогда

2 2 2 (a− c)(b− c)= p = 1⋅p =(−p )(−1)

Следовательно, возможны следующие случаи

{ a − c= 1 { a− c= −p2 b− c= p2 или b− c= −1

Из обеих совокупностей можно получить $b− a =p2− 1,$ из которого можно получить, что $p2 − 1$ не делится на $3.$

Так как $p+ 1$ и $p− 1$ не делятся на $3,$ а среди последовательных $3$ чисел обязательно найдется число, делящееся на $3,$ то $p$ делится на 3. Но $p$ — простое, значит, $p= 3.$

Получаем следующую систему

{ b− a= 8 2 a2+b =1000 =⇒ a +a− 992= 0

Из последнего уравнения получаем, что

{ a= 31 =⇒ b= 39 a= −32 =⇒ b =− 24

Теперь найдем $c$

[ c= a− 1 c= a+ p2 = a+ 9

Тогда $c$ может равняться

⌊ || c= 30 || c= 40 ⌈ c= −23 c= −33

Ответ:

$(31, 39, 30), (−32, −24, −33), (31, 39, 40),(−32, −24, −23)$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#80771

Есть $12$ точек, $7$ из которых лежат на одной окружности в плоскости $α$ , а остальные 5 вне $α$ . Известно, что если четыре точки из всех $12$ лежат в одной плоскости, то эта плоскость — $α.$ Сколько существует выпуклых пирамид с вершинами в этих точках? (Пирамиды считаются различными, если их множества вершин различны.)

Источники: Физтех - 2024, 11.6 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Среди всех возможных пирамид для нас принципиально различаются два случая: когда вершин 4 (тетраэдр) и больше. Посчитаем их по отдельности и затем сложим.

Подсказка 2

Количество всех возможных тетраэдров - количество способов выбрать 4 вершины, за исключением случаев, когда все точки лежат в одной плоскости. Из условия нам известно, что это возможно только когда все 4 вершины принадлежат плоскости 𝜶.

Подсказка 3

У n-угольной пирамиды, где n≥4 основание лежит в плоскости 𝜶, а вершина вне неё. Отдельно посчитаем способы выбрать основание и умножим на количество вариантов выбора вершин.

Подсказка 4

Количество способов выбрать основание находится как сумма числа сочетаний из 7 от 4 до 7, а вершину пирамиды можно взять пятью разными способами. Тогда нужно просто перемножить их и сложить найденное количество тетраэдров и n-угольных пирамид с n≥4

Показать ответ и решение

Посчитаем отдельно количество тетраэдров и выпуклых $n−$ угольных пирамид с $n ≥4.$

Количество тетраэдров это количество способов выбрать $4$ точки, не лежащих одновременно в одной плоскости. Тогда количество тетраэдров равняется

4 4 C12− C 7 = 460

Найдем количество выпуклых $n−$ угольных пирамид с $n≥ 4.$ Основание такой пирамиды лежит в плоскости $α,$ а вершина — вне $α.$ Тогда посчитаем количество оснований. Надо просуммировать все способы выбрать от 4 до 7 вершин без учёта порядка

4 5 6 7 7⋅6⋅5 7⋅6 C 7 +C 7 +C 7 + C7 = 2⋅3 + 2 +7+ 1= 64

Для каждого из посчитанных оснований вершину пирамиды можно выбрать пятью способами, поэтому всего пирамид

5 ⋅64= 320

Итоговый ответ

460 +320= 780

Ответ: 780

Ошибка.
Попробуйте повторить позже

Задача 3#80769

Дан белый клетчатый прямоугольник $100× 400$ . Сколькими способами можно покрасить 8 его клеток в чёрный цвет так, чтобы покрашенное множество клеток было симметрично относительно центра прямоугольника либо одной из его “средних линий” прямоугольника (“средней линией” прямоугольника назовём отрезок, соединяющий середины двух его противоположных сторон). Ответ дайте в виде выражения, содержащего не более трёх членов (в них могут входить факториалы, биномиальные коэффициенты).

Источники: Физтех - 2024, 11.5 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте начнём распутывать клубок симметрий с того, что обозначим за A₁ множество восьмёрок симметричных относительно одной горизонтальной средний линии, за A₂ - вертикальной, за B - относительно центра прямоугольника. Давайте подумаем, сколько нам нужно зафиксировать точек для каждой из симметрий и где, чтобы однозначно восстановить всю восьмёрку?

Подсказка 2

Верно, для A₁ нужны 4 точки не выше (не ниже), чем горизонтальная средняя линия, для A₂ - 4 точки не правее (не левее), чем вертикальная средняя линия, для B - 4 точки в любой одной из указанных ранее областей. Теперь стоит задуматься о том, пересекаются ли данные множества или какая-то комбинация симметрий даёт другую симметрию?

Подсказка 3

Верно, если восьмёрка лежит в любых двух множества A₁, A₂, B, то она лежит во всех трёх, отсюда, вспоминая формулу включений-исключений, мы понимаем, что ответ уже очень близко, осталось только его расписать.

Показать ответ и решение

Назовем восьмеркой набор из $8$ клеток. Пусть $A 1$ — множество восьмерок, симметричных относительной $l 1$ , $A 2$ — относительно $l 2$ , $B$ — относительно центра прямоугольника. $l1$ и $l2$ это средние линии прямоугольника.

Если выбрать какие-то $4$ точки в верхней половине прямоугольника, то остальные точки легко находятся в силу одной из рассматриваемой симметрий относительно $l1, l2$ и центра прямоугольника. Тогда количество элементов во множествах $A1, A2, B$ будет одинаковым. Тогда количество элементов в $A1$ будет равно количеству способов выбрать $4$ очки в одной половине фигуры относительно $l1.$ Остальные $4$ точки будут располагаются в другой половине. Тогда количество способов равняется $4 C100⋅200.$

Если восьмерка лежит сразу в $2$ из $3$ множеств $A1, A2, B,$ то она лежит и в третьей. Это значит, что пересечение двух множеств или пусто, или пересекается с третьим.

Чтобы найти ответ надо найти количество элементов в объединении множеств. Используя формулу включений-исключений, получаем, что

S = |A1∪ A2∪ B|= |A1|+|A2|+|B|− 2|A1∩ A2∩B |,

где $|M |$ — означает количество элементов во множестве $M,$ $S$ — искомое число

Если $2$ точки, лежащие в одной из четвертей прямоугольника, принадлежат пересечению всех $3$ множеств, то легко восстановить исходную восьмерку, удовлетворяющую сразу трем симметриям. Тогда можно посчитать количество элементов в пересечении множеств. Это будет количество способов выбрать $2$ точки в одной из четвертей прямоугольника, образованной $l1, l2$ и центром прямоугольника. Следовательно, количество элементов равняется $C2200⋅50.$

Тогда посчитаем $S$

S = |A1 ∪A2 ∪B|= |A1|+ |A2|+ |B|− 2|A1 ∩A2∩ B|=

= 3C420000− 2C210000

Ответ:

$3C4 − 2C2 20000 10000$

Ошибка.
Попробуйте повторить позже

Задача 4#80764

Из множества $M,$ состоящего из семи подряд идущих натуральных чисел, выбираются шестёрки попарно различных чисел такие, что сумма чисел в каждой из шестёрок — простое число. Пусть $p$ и $q$ — две из таких сумм. Найдите множество $M$ , если $2 2 p − q = 792.$

Источники: Физтех - 2024, 11.4 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте скажем, что первое число - это а и поймем, чему равна сумма во всех шестерках и какие из них могут быть простыми, а какие нет.

Подсказка 2

Тогда у нас получаются суммы шестерок - это числа от 6a + 15, до 6a + 21. Из за делимости на 2 или 3, подходят только числа 6a + 19 и 6a + 17. А это значит, что это ровно наши числа p и q. Остается решить квадратное уравнение на а и найти ответ(подставить значения p и q в равенство).

Показать ответ и решение

Пусть $a$ — наименьшее натуральное число из $M.$ Тогда

M = {a, a+ 1,a+ 2,...,a +6}

Сумма всех $7$ чисел равна

6⋅7 7a+ 1+ 2+ ...+6 =7a+ 2 =7a+ 21

Переберем сумму шестёрок чисел:

. 6a+21 не подходит, так как.. 3 .. 6a+20 не подходит, так как. 2 6a+19 нет противоречий 6a+18 не подходит, так как ... 3 6a+17 нет противоречий .. 6a+16 не подходит, так как. 2 6a+15 не подходит, так как ... 3

Тогда, $p= 6a+ 19, q =6a+ 17.$ По условию задачи $p2 − q2 = 792$ или то же самое, что и

2 2 (6a+19) − (6a+ 17) = 792 =⇒ 2(12a+ 36)=792

2(a+ 3)=396 =⇒ a+3 =33 =⇒ a= 30

Следовательно, $M$ может быть только множеством

{30, 31, 32, 33, 34, 35, 36}

Проверка: $6a +19= 199$ — простое, $6a+ 17= 197$ — простое.

Ответ:

${30, 31, 32, 33, 34, 35, 36}$

Ошибка.
Попробуйте повторить позже

Задача 5#78776

Сколько существует троек целых чисел $(a;b;c)$ таких, что они образуют в указанном порядке геометрическую прогрессию, а их произведение $abc$ равно $150 150 2 ⋅3$ ?

Подсказки к задаче

Подсказка 1

Для начала поймём, а какого вообще вида числа нам подходят? И какие условия на них накладываются?

Подсказка 2

Верно, каждое число при разложении на простые должно представляться в виде: 2ⁿ¹*3ⁿ². И при этом сумма степеней двоек всех трёх чисел должна быть равна 150 и аналогично с тройками! А теперь вспомним условие про геометрическую прогрессию, что можно сказать про число b?

Подсказка 3

Да, b вне зависимости от a и c равно 2⁵⁰*3⁵⁰(это получается из того, что степень b равна полусумме степеней a и c). А что в таком случае можно сказать про a и c?

Подсказка 4

Верно, степень двойки у чисел a и c можно выбрать 101 способом, так как при выборе степени двойки у a — степень c восстанавливается однозначно! И аналогично, для степеней тройки. Получается, что всего таких чисел 101². Но вот, все ли случаи мы учли?

Подсказка 5

Верно, a и c могут быть также отрицательными, тогда просто знаменатель прогрессии поменяется на противоположный!

Показать ответ и решение

Найдём сначала количество троек натуральных чисел. Пусть

x y x y x y a= 2 1 ⋅31, b= 22 ⋅3 2, c= 2 3 ⋅33

где $xi, yi$ — целые неотрицательные числа. Тогда получаем

{ x1+ x2+ x3 =150 y1+ y2+y3 = 150

Числа $a,b,c$ составляют в указанном порядке геометрическую прогрессию тогда и только тогда, когда $b2 =a ⋅c$ , откуда

{ 2x2 = x1+x3 2y2 = y1+ y3

Из полученных уравнений получаем систему

(| x2 = y2 = 50 { x1+ x3 = 100 |( y1+ y3 =100

Посчитаем количество решений этой системы. Есть $101$ способ выбрать пару чисел $(x1;x3)$ . Действительно, $x1$ можно взять любым целым числом из отрезка $[0;100]$ , после чего $x3$ определяется однозначно. Аналогично, пару $(y1;y3)$ можно выбрать $101$ способом. Перемножая, получаем $1012 = 10201$ способ.

Если рассматривать также отрицательные значения переменных, то можно заметить, что подходят все тройки чисел вида $(− a;b;−c)$ , где $a,b,c$ положительны и составляют геометрическую прогрессию. Таких троек ровно столько, сколько и в первом случае, поэтому окончательно имеем $20402$ тройки.

Ответ: 20402

Ошибка.
Попробуйте повторить позже

Задача 6#67590

На координатной плоскости дан параллелограмм с вершинами в точках $O(0;0)$ , $P (− 14;42),Q(6;42)$ и $R(20;0).$ Найдите количество пар точек $A(x1;y1)$ и $B(x2;y2)$ с целыми координатами, лежащих в этом параллелограмме (возможно, на границе) и таких, что $3x2− 3x1 +y2− y1 = 33.$

Источники: Физтех-2023, 11.6 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Сначала может показаться, что задача какая-то жуть. Нужно находить количество пар точек, подходящие под какое-то странное условие... Но давайте понемногу "причёсывать" задачу и понимать, что от нас хотят. Попробуем хорошо преобразовать условие, данное на точки A и B. Какое действие хочется сделать, увидев в одной части координаты и точки A, и точки B?

Подсказка 2

Да, давайте перенесём координаты A в правую часть, а точки B — в левую. Число 33 тоже перенесём влево. Так как координаты у нас целые, то слева и справа получаются тоже какие-то целые значения. Пусть это будет целое число k. Что же теперь означает наше условие на координаты после того, как мы переписали их в удобном виде?

Подсказка 3

Верно, это две параллельные прямые, где вместо x и y мы подставляем координаты точек A и B. То есть мы можем записать уравнение прямых в общем виде с k. Что же нам теперь нужно сделать? Не забудем, что у нас есть ограничение на прямые самой границей параллелограмма. Идейная часть закончилась, теперь уже можно реализовывать техническую часть решения. Вспоминая вопрос задачи, что нам нужно теперь найти?

Подсказка 4

Верно, нам нужно найти в принципе количество целых точек x на прямых вида y=-3x+b. Это с помощью рассмотрения случаев, когда b делится на 3 и не делится, решается несложно(учитывая, конечно, снова ограничение по параллелограмму). Найдя уже до этого ограничения на k, остаётся только дело за комбинаторикой. То есть нам нужно для каждого k, выбрать на прямых нужные нам целые точки.

Показать ответ и решение

Запишем исходное условие на координаты точек $A(x ;y) 1 1$ и $B(x;y ) 2 2$ в виде

3x2+ y2− 33 =3x1+ y1

Так как координаты точек $A(x1;y1)$ и $B(x2;y2)$ являются целыми числами, то левая и правая части этого равенства могут принимать только целочисленные значения $k.$ Пара точек $A(x1;y1)$ и $B(x2;y2)$ с целочисленными координатами удовлетворяет условию тогда и только тогда, когда они лежат на параллельных прямых

y = −3x+ k и y = −3x+ k+ 33

соответственно. Найдём подходящие значения параметра $k.$

Стороны $OP$ и $QR$ параллелограмма лежат на прямых

y =− 3x и y =− 3x+60,

поэтому они параллельны прямым, на которых лежат точки $A (x1;y1)$ и $B(x2;y2).$ Эти прямые пересекают параллелограмм при

( { 0≤ k≤ 60 ( ⇔ k∈[0;27] 0≤ k+ 33 ≤60

Выясним количество точек с целочисленными координатами на каждой из прямых вида

y = −3x+ b

Рассмотрим несколько вариантов:

$1)$ Если $b$ кратно трём (т.е. $b= 3l),$ то получаем прямую

y = 3(−x +l)

При любом целом $x$ получится целое значение $y,$ а чтобы точка оказалась в параллелограмме нужно, чтобы

0≤ y ≤42 ⇔ l− 14≤ x≤ l

При любом $l$ этому неравенству удовлетворяет $15$ целых значений $x.$

$2)$ Если $b$ не делится на 3, т.е. при $b= 3l+ γ,$ где $γ ∈ {1;2},$ имеем

0≤ −3x+ 3l+γ ≤42⇔ l+ γ − 14≤ x≤ l+ γ 3 3

Учитывая, что $x∈ ℤ,$ получаем

l− 13≤ x≤ l

Значит, этому неравенству удовлетворяет $14$ целочисленных значений.

Если $k= 3l$ (таких значений $10),$ то на каждой из двух прямых

y = −3x+ k и y = −3x+ k+ 33

можно выбрать по $15$ точек — всего $10 ⋅15⋅15= 2250$ пар.

Если $k⁄= 3l$ (таких значений $18),$ то на каждой из двух прямых можно выбрать по $14$ точек — имеем $18⋅14⋅14= 3528$ пар.

Итого получаем $2250 +3528= 5778.$

Ответ: 5778

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#67585

Натуральные числа $a,b,c$ таковы, что $ab$ делится на $29310510,bc$ делится на $214313513,$ $ac$ делится на $219318530.$ Найдите наименьшее возможное значение произведения $abc.$

Источники: Физтех-2023, 11.1 (olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Чтобы произведение abc было минимальным, какие простые в своем разложении они могут иметь?

Подсказка 2

Да, каждое из чисел не должно иметь других простых, кроме 2, 3 и 5(но не обязательно, что каждое из них есть). Тогда давайте разложим каждое из чисел a, b, c на простые множители! Какие неравенства можно написать, если внимательно посмотреть на условие задачи?

Подсказка 3

Да, пусть x₁, x₂, x₃ – степени вхождения двойки в a, b, c соответственно, тогда будет верным: x₁ + x₂ ≥ 9; x₂ + x₃ ≥ 14; x₁ + x₃ ≥ 19. Что нужно сделать, чтобы понять в какой степени двойка входит в произведение abc?

Подсказка 4

Верно, нужно сложить эти степени и поделить на 2! Таким образом abc кратно 2²¹(поскольку если мы просто сложим степени двойки, то получим (abc) ²). Так, а дальше осталось сделать то же самое с 3 и 5 и привести пример, что каждая оценка достигается! Но какой случай может вызвать трудности?

Подсказка 5

Ну, если получается нецелое число, то мы его просто округляем до ближайшего целого, это не сложно. А вот, если пример не получается подобрать? Например, в случае с пятеркой: Если сделать также как и с двойками, то получится, что y₁+y₂+y₃ ≥ 27, но при этом y₁+y₃ ≥ 30 и y₂ ≥ 0. Тогда, нужно строить пример для y₁+y₂+y₃ ≥ 30. (y₁, y₂, y₃ – степени вхождения пятёрки в числа a, b, c соответственно)

Показать ответ и решение

Чтобы произведение $abc$ было минимальным, числа $a,b,c$ не должны иметь простых делителей, отличных от $2,3$ и $5.$

Пусть $α1 β1 γ1 a= 2 ⋅3 ⋅5 ,$ $α2 β2 γ2 b =2 ⋅3 ⋅5 ,$ $α3 β3 γ3 c= 2 ⋅3 ⋅5$ (показатели всех степеней — целые неотрицательные числа). Тогда

α+α +α β+ β+β γ+γ +γ abc= 2 1 2 3 ⋅3 1 2 3 ⋅5 1 2 3

Рассмотрим отдельно делимость на $2,3$ и $5:$

$1)$ Из того, что $ab$ делится на $29,$ $bc$ делится на $214,$ $ac$ делится на $219,$ следует, что

(| α1 +α2 ≥9 { α2 +α3 ≥14 |( α1 +α3 ≥19

Складываем полученные неравенства и получаем:

α +α +α ≥ 9-+14+-19= 21 1 2 3 2

Покажем, что значение $α + α + α = 21 1 2 3$ достигается. Для этого возьмём $α =7,α = 2,α =12. 1 2 3$

$2)$ Из того, что $ab$ делится на $10 3 ,$ $bc$ делится на $13 3 ,$ $ac$ делится на $18 3 ,$ следует, что

( |{ β1 +β2 ≥ 10 |( β2 +β3 ≥ 13 β1 +β3 ≥ 18

Складываем полученные неравенства и получаем:

β1+β2+ β3 ≥ 10+-123+18 =20,5

Покажем, что значение $β1+ β2+ β3 =21$ достигается. Для этого возьмём $β1 = 7,β2 = 3,β3 = 11.$

$3)$ Из того, что $ac$ делится на $530,$ следует, что $γ1+ γ3 ≥30.$ Заметим, что

γ1+ γ2+ γ3 ≥γ1+ γ3 ≥ 30.

$γ1 +γ2+ γ3$ может равнятся $30,$ если, например, $γ1 =15,γ2 =0,γ3 = 15.$

Так как минимум каждой из трёх сумм $α1+ α2+α3,β1+ β2+β3,γ1+γ2+ γ3$ не зависит от оставшихся, то и минимальное значение $abc$ равно

abc= 2min(α1+α2+α3)⋅3min(β1+β2+β3)⋅5min(γ1+γ2+γ3) = 221⋅321⋅530

Ответ:

$221⋅321⋅530$

Ошибка.
Попробуйте повторить позже

Задача 8#78777

Найдите количество семизначных чисел, обладающих следующим свойством: сумма остатков от деления числа на некоторые три последовательные степени числа десять равна 12345.

Источники: Физтех-2022, 10.3 (см. olymp-online.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте сначала попробуем понять, а какие степени десятки вообще могли быть, попробуйте перебирать разные случаи и посмотреть, какие точно не могли выполнятся.

Подсказка 2

Верно, степень десятки либо равна 5, либо 6, иначе сумма остатков будет слишком большой или маленькой. Дальше удобно обозначить каждую цифру числа за переменную и записать сумму остатков от деления числа в столбик, тогда нам будет удобно рассуждать о возможных значениях цифр.

Подсказка 3

Не забывайте, что если сумма цифр при сложении в столбик равна 5, то она именно 5, потому как мы всегда берём остаток по модулю 10, когда считаем в столбик, поэтому надо рассматривать ещё случаи, когда она равна 15, 25.

Подсказка 4

Во всех случаях мы найдём какие-то условия на цифры, а некоторые останутся "свободными", т.е. мы можем подставить вместо них любую цифру, причём все эти случаи не пересекаются, и мы можем спокойно их складывать.

Показать ответ и решение

Пусть искомое число есть $abcdefg, (a ⁄=0)$ . Определим, какой может быть максимальная степень десятки, на которую происходит деление. Возможны несколько случаев:

1) если максимальная степень десятки равна $4$ или меньше, то сумма остатков меньше $4 3 2 10 + 10 + 10 = 11100$ , что меньше $12345;$

2) если максимальная степень десятки равна $7$ или больше, то сумма остатков не меньше $6 a⋅10$ , что больше $12345;$

3) максимальная степень десятки равна $5$ или $6$ . Эти случаи возможны.

3.1) Пусть максимальная степень десятки равна $5$ . Тогда остатки от деления на $5 4 3 10, 10 , 10$ равны соответственно $----- ------- cdefg, defg,efg$ , и сумма остатков есть

c⋅104+ 2d⋅103 +3S

где $S = efg, 0≤ S <1000.$

Рассмотрим уравнение $4 3 c⋅10 +2d⋅10 + 3S = 12345$ . Так как $4 12345 <2 ⋅10$ , то либо $c= 0$ , либо $c= 1.$

Если $c= 0$ , то получаем

3 3 2d ⋅10 + 3S = 12345⇒ 2d⋅10 = 12345− 3S = 3(4115− S)

Поэтому $2d$ делится на $3.$ При этом $9< 2d ≤12$ , так как $0≤ S <1000.$ Поэтому $d =6$ , откуда $S = 115$ . То есть число имеет вид $------ ab06115$ . Таких чисел $90.$

Если $c= 1$ , то

2d⋅103+3S =2345.2d⋅103 =2345− 3⋅S

Поэтому либо $d =0$ , либо $d= 1$ . Если $d= 0$ , то $3S = 2345$ , что невозможно. Если $d =1$ , то $3 ⋅S = 345$ , откуда $S = 115$ . То есть число имеет вид $------ ab11115$ . Таких чисел 90.

3.2) Пусть максимальная степень десятки равна $6$ . Тогда остатки от деления на $6 5 4 10 , 10, 10$ равны соответственно $----- ----- bcdefg,cdefg$ , $---- defg$ . И сумма остатков есть

b⋅105 +2c⋅104 +3S

где $---- S = defg, 0≤ S < 10000.$

Рассмотрим уравнение

b⋅105+ 2c⋅104+ 3S = 12345.

Это равенство возможно только при $b= c= 0$ . Значит, $3S = 12345$ , откуда $S = 4115$ , то есть число имеет вид $------ a004115$ . Таких чисел $9.$

Значит, искомое количество семизначных чисел есть $90+ 90+ 9= 189.$

Ответ: 189

Ошибка.
Попробуйте повторить позже

Задача 9#33372

Найдите количество троек натуральных чисел $(a;b;c)$ , удовлетворяющих системе уравнений

{ HO Д(a;b;c)=6, HO К(a;b;c)=215⋅316.

Подсказки к задаче

1) Рассмотрим разложене на простые

2) НОД как-то выбирает каждую степень простого, как и НОК, как же он это делает?

Показать ответ и решение

Пусть $a =2α1 ⋅3α2,b= 2β1 ⋅3β2,c= 2γ1 ⋅3γ2$ (никаких других простых множителей числа $a$ , $b,c$ содержать не могут - иначе нарушается второе условие системы). Отсюда

max(α ;β ;γ) max(α ;β ;γ ) min(α ;β ;γ ) min(α ;β ;γ ) HOK (a;b;c)= 2 1 1 1⋅3 2 2 2, HOД(a;b;c)= 2 1 1 1 ⋅3 2 2 2.

Учитывая данную в условии систему, получаем соотношения

{ max(α1;β1;γ1)= 15, { max (α2;β2;γ2)= 16, min(α1;β1;γ1)= 1 и min(α2;β2;γ2)=1. (1)

Рассмотрим первую систему $(1)$ . Возможны следующие наборы чисел $(α1;β1;γ1)$ :

$(1;1;15)− 3$ набора (за счёт различных перестановок этих чисел);

$(1;15;15)$ — также три набора;

$(1;k;15)$ , где $2 ≤k ≤14−$ есть $13$ различных значений $k$ и для каждого из них $6$ перестановок — всего $78$ вариантов.

Итак, есть $3+ 3+6 ⋅13= 84$ способа выбрать тройку чисел $(α1;β1;γ1)$ . Аналогично устанавливаем, что для выбора $(α2;β2;γ2)$ есть $3+ 3+ 6⋅14= 90$ ( $2 ≤k ≤15$ — $14$ значений) способов. И поскольку один выбор осуществляется независимо от другого, то общее количество способов равно $84⋅90 =7560$ .

Ответ:

$7560$

Критерии оценки

Найдено количество троек для степеней одного из простых чисел только в одном случае – 2 балла.

Получено одно или оба соотношения вида {︃ max (𝛼1; 𝛽1; 𝛾1) = 𝑘, min (𝛼1; 𝛽1; 𝛾1) = 1 и {︃ max (𝛼2; 𝛽2; 𝛾2) = 𝑚, min (𝛼2; 𝛽2; 𝛾2) = 1. и других продвижений нет – 1 балл за задачу (этот балл не суммируется с указанным выше).

Неарифметическая (комбинаторная) ошибка (вместо правила произведения применено правило суммы, некоторые случаи посчитаны дважды или пропущены и т.п.) – не более 1 балла за задачу.

Неверно решена «числовая часть» (из условия сделаны неверные выводы, например, утверждается, что одно из чисел должно равняться произведению 𝑝^𝑚𝑎𝑥 𝑞^𝑚𝑎𝑥 или 𝑝𝑞; используются неверные утверждения, например, НОД(𝑎, 𝑏, 𝑐) НОК(𝑎, 𝑏, 𝑐) = 𝑎𝑏𝑐) – 0 баллов за задачу.

Ошибка.
Попробуйте повторить позже

Задача 10#67075

Найдите количество восьмизначных чисел, произведение цифр которых равно $1400.$ Ответ необходимо представить в виде целого числа.

Источники: Физтех-2020, 10.1, (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Разложим 1400 на простые множители, чтобы посмотреть, какие вообще наборы цифр есть для того, чтобы составить нужные по условию числа.

Подсказка 2

Отлично, получается 3 набора: "22255711", "42557111" и "85571111". Перестановкой цифр в каждом наборе мы получаем нужное число. Поработаем с первым набором: допустим, в нем все цифры разные, тогда подошло бы 8! чисел. Но теперь заметим, что не все цифры одинаковые, например, двойки повторяются 3 раза. Это значит, что на самом деле подходящих чисел в 3! раз меньше. То же проделаем и с пятерками (и с единичками тоже).

Подсказка 3

Отлично, в первом наборе получили 8! / (3! * 2! * 2!) вариантов. Аналогично считаем варианты и в втором, и в третьем наборах. Теперь остается сложить все эти варианты и получить итоговый ответ.

Показать ответ и решение

Разложим $1400$ на множители. $1400= 5⋅280= 52⋅56 =52⋅7⋅8= 23⋅52⋅7.$ Значит, искомые числа могут состоять из следующих цифр: а) три двойки, две пятёрки, одна семёрка и две единицы, б) четвёрка, двойка, две пятёрки, одна семёрка и три единицы или в) восьмёрка, две пятёрки, одна семёрка и четыре единицы.

В первом случае способов выбрать места для двоек можно $3 8⋅7⋅6 C8 = 3!$ способами, так как нам нужно выбрать три места из восьми для двоек. Затем выбрать места для пятёрок $2 5⋅4 C5 = 2!$ вариантов, затем одно из трёх оставшихся мест для семёрки $3$ способами, а остальные места займут единицы, поэтому всего в этом случае $8⋅7⋅6 5⋅4 3! ⋅ 2! ⋅3= 1680$ вариантов.

В втором случае способов рассуждения абсолютно аналогично для трёх единиц, двух пятёрок, семёрки, но дальше есть ещё 2 способа выбрать место двойке, а оставшееся место занимает четвёрка. В этом случае $1680⋅2$ вариантов.

В третьем случае выбрать места для единиц можно $4 8⋅7⋅6⋅5 C8 =--4!--$ способами, далее для двух пятёрок $2 4⋅3 C4 =-2$ способа, оставшиеся восьмёрку и семёрку ставим двумя способами. Всего получается $70⋅6⋅2= 840$ вариантов.

Итого $1680⋅3+ 840 =5880$ вариантов.

Ответ:

$5880$

Ошибка.
Попробуйте повторить позже

Задача 11#45521

Бросили $70$ игральных костей (кубиков с цифрами от $1$ до $6$ на гранях, вероятность выпадения каждой из граней одна и та же) и посчитали сумму выпавших чисел. Какая из вероятностей больше: того, что сумма больше $350$ , или того, что сумма не больше $140?$

Подсказки к задаче

Подсказка 1!

Заметим одну важную вещь! Как изменится сумма чисел, выпавших на всех костях, если вместо каждого числа выпадет его "дополнение до 7"? То есть вместо 1 - 6, 2 - 5 и так далее?

Подсказка 2!

Верно, если сумма была S, то сумма нового набора - 490 - S! Таким образом, все наборы ( в частности, наборы с суммой 140 и 350) разбиваются на пары! А что это значит в контексте вероятности?

Подсказка 3!

Что вероятность выпадения набора с суммой S и c суммой 490 - S одинакова! Отлично, осталось внимательно теперь рассмотреть вероятности, о которых говорится в условии)

Показать ответ и решение

Пусть выпал некоторый набор $a ,...a ,∑ a = a. 1 70 i$ Заметим, что если на каждом кубике выпадет инвертированное число $b = 7− a i i$ (что всегда возможно), то сумма будет равна $7⋅70− a =490− a.$ Вероятность набора $ai$ равна вероятности набора $bi$ (все исходы в точности разбиваются на такие пары). Кроме того, $∑ ∑ ∑ P[ ai ≤ 140]= P[490 − bi ≤ 140]= P[ bi ≥ 350],$ откуда $∑ ∑ P[ ai ≤140]>P [ bi > 350],$ больше вторая вероятность из условия.

Ответ:

того, что сумма не больше $140$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#33641

Монету подбрасывают $90$ раз (вероятности выпадения орла и решки в каждом броске одинаковы). Пусть $p$ — вероятность того, что орёл выпадет не меньше $55$ раз, а $q$ — вероятность того, что орёл выпадет меньше $35$ раз. Найдите $p− q$ .

Источники: Физтех-2020, 11.1, (см. olymp.mipt.ru)

Показать ответ и решение

В силу того, что выпадение орла и решки равновозможны, вероятность получить $90$ орлов равна вероятности получить $90$ решек (т.е. $0$ орлов); вероятность получить $89$ орлов равна вероятности получить $89$ решек (т.е. одного орла) и т.д. Обозначим вероятность, что выпало ровно $k$ орлов через $pk$ . Тогда $p =p55+ p56+ ...+ p90,q = p0+p1+ ...+ p34$ , а в силу сказанного выше, $q =p90+ p89+ ...+ p56$ . Значит, $p − q = p55$ .

Посчитаем вероятность того, что орёл выпадает ровно $55$ раз при $90$ бросках. Если обозначить выпадение орла единицей, а выпадение решки нулём, то каждую последовательность из $90$ бросков можно охарактеризовать последовательностью цифр из нулей и единиц. Вероятность получить любую из таких последовательностей равна $-1- 290$ . Нас устроят все те последовательности событий, которые содержат ровно $35$ единиц. Их количество равно $35 C90$ (выбираем из имеющихся $90$ позиций $35$ позиций для единиц без учёта порядка, после чего остальные позиции заполняются нулями). Значит, вероятность получить хотя бы одну такую последовательность равна $1 35 290 ⋅C90$ . Это и есть $p55$ .

Ответ:

$-1-⋅C35 290 90$

Ошибка.
Попробуйте повторить позже

Задача 13#30937

Найдите количество восьмизначных чисел, произведение цифр каждого из которых равно $3375.$ Ответ необходимо представить в виде целого числа.

Источники: Физтех-2020, номер 1, (см.olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Если произведение 8 цифр это 3375, то надо выяснить, какие это могут быть цифры вообще и сколько раз они встречаются в записи числа.

Подсказка 2

Ага, получилось два набора цифр: в одном пятерки, тройки и единички, в другом есть помимо них девятка. Находим, сколько в первом наборе способов поставить тройки, потом на оставшиеся места пятерки и тд, то же делаем для второго набора и понимаем, что эти наборы не пересекаются -> работает правило сложения

Показать ответ и решение

Разложим $3375$ на множители. $3375 =5⋅675= 52⋅135= 53⋅27= 53⋅33.$ Значит, либо в нашем числе есть $3$ пятерки, $3$ тройки и остальные единицы, либо в нашем числе есть $3$ пятерки, $1$ девятка, $1$ тройка и остальные единицы.

В первом случае способов выбрать места для пятерок можно $3 8⋅7⋅6 C8 = 3!$ способами, так как нам нужно выбрать три места из восьми для пятерок. Затем выбрать места для троек $3 5⋅4⋅3 C5 = 3!$ вариантов, а остальные места займут единицы, поэтому всего в этом случае $8⋅7⋅6 5⋅4⋅3 3! ⋅ 3! =56⋅10= 560$ вариантов.

В втором случае способов выбрать места для пятерок так же $3 8⋅7⋅6 C8 = 3! ,$ выбрать место для тройки можно из оставшихся пяти, для девятки — из оставшихся четырёх, а остальные места займут единицы, поэтому всего в этом случае $8⋅7⋅6 3! ⋅5⋅4= 56⋅20= 1120$ вариантов.

Итого $1120+ 560 =1680$ вариантов.

Ответ:

$1680$

Ошибка.
Попробуйте повторить позже

Задача 14#30938

На столе лежат $130$ различных карточек с числами $502,504,506,...,758,760$ (на каждой карточке написано ровно одно число, каждое число встречается ровно один раз). Сколькими способами можно выбрать $3$ карточки так, чтобы сумма чисел на выбранных карточках делилась на $3?$

Подсказки к задаче

Подсказка 1

Так, нас просят выбрать три числа так, чтобы их сумма делилась на три. В таком случае, какие остатки должны быть у чисел при делении на 3?

Подсказка 2

Да, числа должны давать либо одинаковые остатки, либо наоборот различные(0, 1, 2). Можно ли посчитать, какие остатки при делении на 3 дают числа в условии задачи?

Подсказка 3

Да, можно, так 502 ≡ 1 (mod=3), 504 ≡ 0 (mod=3), 506 ≡ 2(mod=3), …, 760 ≡ 1(mod=3). То есть, по модулю 3: 44 числа сравнимы с единицей, 43 числа сравнимы с двойкой, 43 числа сравнимы с нулем. Как посчитать общее число способов?

Подсказка 4

Выбрать три числа с разными остатками, это просто 43*43*44. А если мы хотим выбрать три числа с одинаковым остатком, то нужно воспользоваться формулой числа сочетаний. И посчитать сумму всех этих способов!

Показать ответ и решение

Первое решение.

Если мы возьмём три карточки с числами подряд по возрастанию, то среди них будут по одной карточке с остатками $0,1$ и $2$ при делении на $3.$ Значит, среди карточек $502,504,506,...,758$ по $43$ карточки с каждым остатком (разобьём на $43$ тройки подряд идущих) и ещё есть карточка с числом $760,$ которое дает остаток $1.$

Давайте подумаем, какие есть варианты для остатков трёх карточек, чтобы их сумма делилась на $3:$ либо все три числа должны давать разные остатки (способов выбрать так карточки $43 ⋅44⋅43,$ так как выбрать карточку с остатком $0$ — $43$ способа, способов выбрать карточку с остатком $1$ — $44$ и способов выбрать карточку с остатком $2$ — $43$ ), либо все три остатка $0$ (тогда способов $3 C 43),$ либо все три остатка 1 (тогда способов $3 C44),$ либо все три остатка $2$ (тогда способов $3 C43).$ Итого всего

43⋅44⋅43+C343+ C344+ C343 = 81356+ 12341+ 13244+ 12341= 119282

Второе решение.

Данные числа, расположенные в порядке возрастания, образуют арифметическую прогрессию с разностью $2≡3 −1.$ Следовательно, остатки от деления на $3$ у этих чисел чередуются (идут по убыванию с шагом $1,$ то есть $0→ 2→ 1→ 0→ ...$ ).

Среди данных нам чисел есть $44,$ дающие остаток $1$ от деления на $3$ (они образуют множество $A ={502;508;514;...;760}$ ), $43$ числа, делящихся на $3$ (образуют $B = {504;510;516;...;756}$ ) и $43$ числа, дающих остаток $2$ от деления на $3$ ( $C ={506;512;518;...;758}$ ).

Сумма трёх чисел может делиться на $3$ в следующих случаях.

1.: Все три числа дают одинаковые остатки от деления на $3.$ Есть $C344$ способов выбрать $3$ числа из множества $A$ и по $C343$ способов выбрать $3$ числа из множеств $B$ и $C.$ В сумме получаем $44⋅436⋅42+ 2⋅ 43⋅462⋅41-=13244+2 ⋅12341= 37926$ способов.
2.: Если не все остатки одинаковы, то подходит только случай, когда все три остатка разные, т.е. мы должны выбрать по одному числу из каждого из множеств $A,B,C.$ Получаем $44 ⋅43⋅43= 81356$ способов. Если есть два равных остатка, то для кратности их суммы трём третий должен быть таким же.

В сумме выходит $119282$ способов.

Ответ:

$119282$

Ошибка.
Попробуйте повторить позже

Задача 15#67076

Даны $6000$ карточек, на которых написаны натуральные числа от $1$ до $6000$ (на каждой карточке написано ровно одно число, притом числа не повторяются). Требуется выбрать две карточки, для которых сумма написанных на них чисел делится на $100.$ Сколькими способами это можно сделать?

Источники: Физтех-2018, 10.1 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Посмотрим на все эти числа по модулю 100 - тогда останется по 60 карточек каждого остатка по модулю 100. Как можно получить 0? Например, 0+0. Или 50+50. Посчитаем сначала количество таких вариантов по отдельности: сначала 0+0, а затем 50+50.

Подсказка 2

Количество вариантов для 0 и для 50 будет одинаково: это С₆₀² (берем две любые карточки из 60). Как еще получить 0? 1+99 = 2 + 98 и тд - все это будет равно нулю по модулю 100, что нам и надо. Посчитаем ситуацию 1+99: для каждой карточки 1 подходит каждая карточка 99, их по 60 штук, следовательно вариантов здесь 60². Причём здесь посчитаны и варианты 99+1.

Подсказка 3

Так мы подсчитываем 49 раз, вернее, посчитали мы всего один раз и умножили на 49, так как ответ везде получился одинаковый. Все полученные комбинации нам остается лишь сложить :)

Показать ответ и решение

Будем брать карточки по очереди. Возможны несколько случаев в зависимости от того, какое число написано на первой карточке.

$1)$ Номер на карточке оканчивается на $00$ (таких карточек $60$ штук). Для делимости суммы на $100$ вторую карточку надо выбрать так, чтобы номер на ней также оканчивался на $00.$ Всего получаем $2 60⋅59 C60 = 2 = 1770$ вариантов.

$2)$ Аналогично, если номер на карточке оканчивается на $50$ (таких карточек также $60$ штук), то для делимости суммы на $100$ вторую карточку надо выбрать так, чтобы номер на ней оканчивался на $50,$ т.е. и здесь $1770$ вариантов.

$3)$ Номер на карточке оканчивается на число от $1$ до $49$ (таких карточек $49⋅60= 2940$ ). Для каждой из них пару можно выбрать $60$ способами (если число оканчивается на $1,$ то подойдёт любая карточка с числом, оканчивающимся на $99;$ если число оканчивается на $2$ — любая карточка с числом, оканчивающимся на $98$ и т.д.). Таким образом, получаем $2940⋅60= 176400$ вариантов.

$4)$ Номер на карточке оканчивается на число от $51$ до $99.$ Все такие варианты были учтены при рассмотрении третьего случая (эти карточки составляли пару карточкам, выбранным первоначально).

Итого выходит $1770+1770+ 176400= 179940$ способов.

Ответ:

$179940$

Ошибка.
Попробуйте повторить позже

Задача 16#39647

Даны $2117$ карточек, на которых написаны натуральные числа от $1$ до $2117$ (на каждой карточке написано ровно одно число, притом числа не повторяются). Требуется выбрать две карточки, для которых сумма написанных на них чисел делится на $100$ . Сколькими способами это можно сделать?

Источники: Физтех-2018, 10.1 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Понятно, что надо будет как-то смотреть на остатки по модулю 100 и складывать их. Понятно, что число делится на 100, когда сумма будет оканчиваться двумя нулями. В любом случае придётся рассмотреть случаи, поэтому систематизируем их. Давайте начнём с самого простого, когда цифры оканчиваются либо на 50, либо на 00. Сколько же таких карточек в принципе и какую карточку в пару нужно выбирать?

Подсказка 2

Верно, карточек каждого вида по 21 и в пару мы выберем такую же, для сохранения делимости. Получаем, что в каждом виде таких пар будет 21*20/2. Дальше видим, что у нас не очень удачно выбрано ограничение по числам. Давайте сразу разберёмся с карточками с 2101 до 2117. Подумайте над тем, какие числа снова можно подобрать к ним в пару и сколько их?

Подсказка 3

Точно, их тоже по 21 штуке для каждой. То есть количество таких пар будет равно 17*21. Остались карточки с 1 до 2099 и уже можно увидеть какие пары нам нужны. То есть в пару к 01 мы берём 99, к паре 02 - 98 и так далее до 49 и 51. Осталось только понять, сколько для выбранного первого числа есть второе в пару. И умножить это количество выборов первого числа!

Показать ответ и решение

Будем называть парной карточкой к данной такую карточку, что их сумма кратна $100$ , а видом карточки — её последние две цифры. Рассмотрим несколько случаев

Номер на карточке кратен $50$ , то есть заканчивается на $50$ или $00$ . Карточек каждого вида ровно по $21$ , а парная карточка к каждой из них заканчивается на те же самые две цифры. То есть для обоих видов мы получим по $C2 21$ способов взять две парные карточки с такими последними цифрами. Всего $21 ⋅20= 420$ .
Номер карточки заканчивается на $01,02...49$ , при этом он не больше $2100$ . В силу второго ограничения таких карточек тоже по $21$ каждого вида. Легко видеть, что в пару им идут виды $51,52...99$ , по одному на каждый, то есть для каждой выбранной карточки подойдёт $21$ карточка парного вида. Итак, выбираем вид $49$ способами, затем его представителя $21$ и пару ему также $21$ , итого $2 21 ⋅49$ .
Остались карточки с номерами $2101,...2117$ . Для каждой из них есть по $21$ парной, то есть получаем $17⋅21$ способов.

Складывая по всем случаям, получаем $420+ 212⋅49+ 17⋅21 =22386$ способов.

Ответ:

$22386$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#38064

На каждой из прямых $y =1$ и $y =6$ отмечено по $200$ точек с абсциссами $1,2,3,...,200.$ Сколькими способами можно выбрать три точки из отмеченных $400$ так, чтобы они являлись вершинами прямоугольного треугольника?

Источники: Физтех-2018, 11.3, (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Давайте подумаем какие два разных случая бывают в этой задаче. Как этот прямоугольный треугольник может располагаться относительно этих прямых?

Подсказка 2

Да, либо один из его катетов лежит полностью на прямой, либо гипотенуза. Как можно посчитать кол-во способов, когда катет лежит на одной из прямых? Что тогда можно сказать про другой катет?

Подсказка 3

Конечно, можно сначала посмотреть на другой катет, который перпендикулярен обеим прямым. То есть, нам надо выбрать абсциссу(200 способов), а потом точку на одной из прямых. Этих точек осталось 200*2-2=199*2. Значит всего способов в этом случае 400*199. Но это первый случай. А как свести к перебору второй случай, когда гипотенуза лежит на одной из прямых? Какой отрезок в таком треугольнике точно известен? Что он дает?

Подсказка 4

Верно, высота из прямого угла. Она всегда будет равна 5. А еще, ее квадрат равен произведению двух проекций катетов, которые являются натуральными числами. Какими они тогда могут быть, если их произведение равно 25?

Подсказка 5

Действительно, либо 1 и 25 либо 5 и 5. Теперь подумаем, как нам посчитать каждый из способов. В первом случае мы должны учесть порядок проекций. То есть сначала идет отрезок длиной 1, а потом 25 или наоборот. Плюсом, учесть прямую на которой располагается гипотенуза. Плюсом, учесть, что гипотенуза не должна выходить за крайние точки на прямых. Во втором же случае порядок нам не важен, так как отрезки проекций катетов равны, а все остальное важно. Остается посчитать это, сложить с первым случаем(когда катет лежит на одной из прямых) и получить ответ.

Показать ответ и решение

Первое решение.

Треугольники делятся на два типа

Катеты параллельны осям. Тогда один из них соединяет точки с одинаковой абсциссой, а второй лежит на какой-то прямой. Выберем эту абсциссу $200$ способами, а затем прямую и саму точку $2⋅199$ способами (сначала прямую, а затем точку из оставшихся $199$ на ней). В итоге $400⋅199$ способов.
Ни один из катетов не лежит на прямых, поэтому там лежит гипотенуза (ведь на какой-то прямой лежат две вершины треугольника), откуда высота к ней имеет длину $5$ . Она же является корнем из произведения проекций катетов, то есть их произведение равно $25 =5⋅5 =1⋅25$ — длины проекций являются натуральными числами, потому их значения могут быть только такими. Если это $1$ и $25$ , то, выбирая прямую, затем порядок двух различных отрезков проекций на прямой, а затем абсциссу высоты, получаем $2⋅2⋅174$ способа (поскольку мы не можем брать $25$ ближайших точек с одной стороны прямой, а с другой одну, чтобы наши проекции “влезли”). Если же это $5$ и $5$ , то сначала выбираем прямую, порядок выбирать не нужно, поскольку отрезки равны, а точку выберем $190$ способами, поскольку с каждой стороны прямой нельзя брать по $5$ точек. В итоге $190⋅2+ 174⋅4$ способа.

В качестве ответа имеем $400⋅199+190⋅2+ 174 ⋅4 =80676$ .

Второе решение.

Рассмотрим два возможных случая:

Гипотенуза треугольника лежит на одной из прямых, а вершина прямого угла - на второй прямой. Пусть $ABC$ - данный треугольник с прямым углом при вершине $C,CH$ - его высота, опущенная на гипотенузу. Из пропорциональности отрезков прямоугольного треугольника получаем, что $2 CH = AH ⋅BH$ , т.e. $AH ⋅BH =25$ . Поскольку $AH$ и $BH$ - целые числа, то возможны следующие случаи: $AH =BH = 5,AH = 25$ и $BH = 1,AH =1$ и $BH =25$ .
В первом из этих случаев гипотенузу $AB$ , равную 10, можно расположить $190⋅2= 380$ способами (по $200 − 10$ способов расположения на каждой из двух данных прямых), при этом положение вершины $C$ определяется однозначно.
Во втором и третьем случаях длина гипотенузы равна 26, и её можно расположить $2(200−$ $26)= 348$ способами. Для каждого положения гипотенузы существует два способа размещения вершины - получаем $2⋅348= 696$ способов.
Один из катетов треугольника (назовём его $BC$ ) перпендикулярен данным прямым, а второй катет $(AC )$ лежит на одной из данных прямых. Тогда положение катета $BC$ можно выбрать 200 способами. Для каждого варианта расположения катета $BC$ вершину $A$ можно расположить 398 способами (подходят все точки кроме уже выбранных $B$ и $C$ ) - всего выходит $200⋅398=79600$ способов.

Итого получаем $380+696+ 79600= 80676$ способов.

Ответ:

$80676$

Критерии оценки

Доказано, какие три вида прямоугольных треугольников возможны — 2 балла.

Если получено не более двух видов треугольников или разобраны все три случая, но не обосновано отсутствие других возможностей, то этот пункт оценивается в 0 баллов.

Произведён подсчёт количества треугольников одного вида — 1 балл.

Произведён подсчёт количества треугольников двух видов — 2 балла.

Произведён подсчёт количества треугольников трёх видов — 4 балла.

Ошибка в $\pm 1$ при подсчёте количества треугольников — снять 1 балл от общей суммы.

Отсутствует умножение на два (т. е. считается, что гипотенуза и/или катет треугольника может лежать только на одной из двух данных прямых) — снять 2 балла от общей суммы.

Верный ответ в развёрнутой форме — баллы не снимаются.

Ошибка.
Попробуйте повторить позже

Задача 18#31509

Есть $200$ различных карточек с числами $2,3,22,32,...,2100,3100$ (на каждой карточке написано ровно одно число, каждое число встречается ровно один раз). Сколькими способами можно выбрать $2$ карточки так, чтобы произведение чисел на выбранных карточках было кубом целого числа?

Источники: Физтех-2019, 10.5, (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

По сути 2^1 и 2^4 дают нам одно и то же при умножении на какое-то число - либо это в обоих случаях куб, либо в обоих нет. А как мы вообще можем разбить все данные числа на группы с одинаковыми свойствами?

Подсказка 2

Да, числа вида 2^1, 2^4, .. 2^100 будут в одной группе, 2^2, 2^5, .. 2^98 в другой, так же с 2^3, так же и с тройками, получилось 6 групп. Выбирая по одному числу из каждой группы, можно ли понять, будет куб или нет?

Подсказка 3

Да, можем. Например, при перемножении 2^2 и 2^1 куб получился -> значит можно комбинировать числа этих групп. Найдите все возможные подходящие комбинации групп и посчитайте количества способов, помня про правила умножения и сложения и используя наши любимые цэшки :)

Показать ответ и решение

Чтобы число было кубом, нужно, чтобы степень каждого числа делилась на $3$ . Если мы возьмем одну карточку со степенью $2$ и одну со степенью $3$ , то они в произведении будут кубом только, если изначальные степени были кубами. Значит, в этом случае у нас $33⋅33$ варианта.

Если на обеих карточках степени двойки, то нужно посмотреть на остаток этих степеней при делении на $3$ . Степени могут давать остатки $1$ и $2$ или $0$ и $0$ . В первом случае у нас получится $34⋅33$ вариантов (нам важен порядок), во втором случае у нас получится $33⋅32∕2$ варианта (делим на $2$ , потому что здесь порядок уже не важен). Полностью аналогично со степенями тройки.

Получаем ответ $33⋅33 +2⋅(34⋅33 +33⋅32∕2)= 33⋅33+2 ⋅33⋅50= 33⋅133$ .

Ответ:

$4389$

Ошибка.
Попробуйте повторить позже

Задача 19#31834

Дано число $5300...0035$ ( $100$ нулей). Требуется заменить некоторые два нуля на ненулевые цифры так, чтобы после замены получилось число, делящееся на $495$ . Сколькими способами это можно сделать?

Источники: Физтех-2017, 11.5 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Так как мы рассматриваем делимость на 495, посмотрим сначала его разложение на простые множители, 495=5*11*9. Наше же число уже оканчивается на 5, поэтому осталось проконтролировать делимость на 9 и 11. Если с делимостью на 9 всё относительно просто, то вот с 11 посложнее, потому что делимость зависит от чётности. Тогда какие два случая резонно рассмотреть, чтобы проконтролировать это?

Подсказка 2

Верно, можно рассмотреть случаи, когда мы меняем 0 на позиции одной чётности и на разных. Так будет намного удобнее, и, конечно, они не пересекаются между собой. Посмотрим сначала первый случай. Что тогда можно сказать про позиции 5 и 3 и сумму цифр числа? Как они влияют на делимость на 9 и 11?

Подсказка 3

Верно, 5 и 3 находятся на позициях с разной чётностью, а значит никак не влияют на делимость на 11. То есть мы должны менять нули на цифры с суммой 11. А что с делимостью на 9? С ней всё ок, так как 5+5+3+3+11=27. Осталось только найти количество способов выбрать позиции одной чётности и умножить на количество представлений числа 11. Теперь что можно сразу сказать про второй случай, зная информацию из этой подсказки?

Подсказка 4

Ага, раз теперь позиции разной чётности, то и разность должна делится на 11. Другими словами цифры должны быть равны(цифры не превышают 9). А что с делимостью на 9? Наша сумма равна 16+2х, где х – это цифра, на которую поменяли нули. Посмотрите, чему может равняться х, и аналогично найдите количество способов выбрать две позиции разной чётности без учёта порядка.

Показать ответ и решение

Поскольку $495 =5 ⋅9⋅11$ , а данное в условии число уже оканчивается на $5$ , то достаточно добиться делимости на $11$ и на $9$ . Рассмотрим два случая:

Пусть мы меняем нули на позициях одной чётности. Тогда сумма поставленных нами ненулевых цифр точно не меньше $2$ и не больше $18$ , а при этом должна быть кратна $11$ , поскольку остальные цифры в знакопеременную сумму дают $0$ . Отсюда сумма поставленных нами цифр в точности должна быть равна $11$ , причём тогда сумма всех цифр будет равна $11+ 5+ 3+3 +5 =27$ и кратна $9$ . Тогда и число будет делиться на $9$ . Способов выбрать две позиции одной чётности с учётом порядка (потому что мы будем ставить разные цифры, ведь $11$ не делится пополам, а при постановке разных цифр нам уже важно, в каком они стоят порядке: получаются разные числа) будет $100 ⋅49$ (первая позиция любая, а вторая из оставшихся позиций той же чётности номера), умножая это на количество разбиений числа $11$ в сумму двух цифр уже без учёта порядка ( $11= 2+ 9= 3+ 8=4 +7 =5+ 6$ ), имеем $4⋅100⋅49$ способов.
Теперь рассмотрим позиции разной чётности. Теперь из признака делимости на $11$ поставленные нами две цифры должны быть равны (чтобы знакочередующаяся сумма цифр давала ноль и делилась на $11$ ), а сумма цифр полученного числа будет равна $16+ 2k$ , где $k ∈[1,9]∩ℕ$ , и должна делиться на $9$ , отсюда подойдёт только $k= 1$ . Осталось выбрать две позиции разной чётности без учёта порядка (ведь мы ставим одинаковые цифры и числа получаются одинаковые, хоть мы поставим $k...k$ , хоть $k...k$ ) $100 ⋅50∕2= 502$ способами (первая позиция любая, а вторая любая из позиций с номерами другой чётности).

В качестве ответа имеем $502+ 400 ⋅49 =22100$ .

Ответ:

$22100$

Ошибка.
Попробуйте повторить позже

Задача 20#30940

На координатной плоскости рассматриваются квадраты, все вершины которых имеют целые неотрицательные координаты, а центр находится в точке $(60;45)$ . Найдите количество таких квадратов.

Источники: Физтех-2017, 11.5 (см. olymp.mipt.ru)

Подсказки к задаче

Подсказка 1

Попробуйте сместить оси координат в центр квадрата. Что тогда можно сказать про координаты его вершин?

Подсказка 2

Да, мы поняли, что координаты его вершин имеют вид (a,b),(-b,a),(-a,b),(b,-a). Но это при смещенных координатах(мы переместили центр из точки (0;0) в точку (60;45)). Вернем центр координат туда, где он был, и поймём, как изменились значения.

Подсказка 3

Конечно, к каждым координатам по Ох прибавилось 60, а к каждым по Оу прибавилось 45. Как теперь можно оценить a и b, используя условие о том, что координаты вершин квадрата-целые неотрицательные числа?

Подсказка 4

Да, мы получили, что |a|<=45 и |b|<=45. Все ли пары (a,b) нам подходят и не посчитали ли мы что-то несколько раз?

Подсказка 5

Нам не подходит пара (a,b)=(0,0), так как тогда это не квадрат. И также мы считаем все остальные пары по 4 раза. Остаётся посчитать итоговый ответ!

Показать ответ и решение

Проведем через 2 вершины и центр квадрата прямые, параллельные осям, как на картинке.

$PIC$

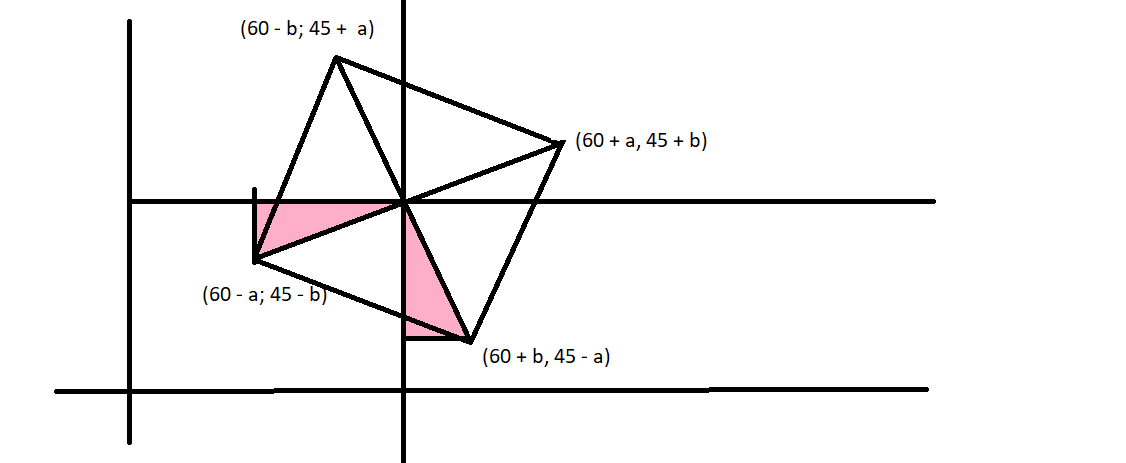
Заметим, что выделенные на картинке цветом треугольники равны по двум углам и стороне. Значит, если одна вершина с координатами $(60− a;45− b)$ , то следующая $(60+b;45− a)$ , затем по аналогичным соображениям следующая вершина $(60+a;45+ b)$ и последняя $(60− b;45+a)$ . Тогда из условия, что все координаты неотрицательные получаем, что числа $60− a, 45− b, 60+ b, 45− a, 60+a, 45+ b, 60− b, 45 +a$ неотрицательны. Отсюда $|a|≤ 45$ и $|b|≤ 45$ . Значит, для значения $a$ у нас $91$ вариант и для значения $b$ у нас $91$ вариант, но если $a =b= 0$ , то не получится квадрат. Итого: $2 91 − 1$ вариантов для пар $(a,b)$ , но заметим, что в квадрате изначальную вершину можно выбрать четырьмя способами. Значит, четырём парам значений $a$ и $b$ соответствует один квадрат. Таким образом, квадратов $912−1 4 = 2070$ .

Ответ:

$2070$

Предыдущий раздел

Следующий раздел