Ошибка.
Попробуйте повторить позже
В треугольник со сторонами
,
вписана окружность с центром в точке
, которая касается сторон
и
в точках
и
соответственно. На прямой
отмечена точка
так, что угол
равен
. Найдите длину отрезка
.
Подсказка 1
Во-первых, давайте поймём, что у нас за картинка. А картинка у нас фиксирована, то есть мы можем вычислить (возможно, с большой сердечной болью) любой объект на картинке. А значит, скорее всего, задача на счёт. При этом, если мы уже хотим считать, то давайте посчитаем углы треугольника (возможно, угол OAK равен 60 градусам неспроста, иначе, непонятно как связать его хоть с чем-то)
Подсказка 2
По теореме косинусов угол ABC равен 60 градусам. Значит, угол AOC — 120. То есть, прямые OC и AK параллельны, а где параллельность — там и подобие. Очевидно, что сторона MT ищется, так как известен угол и можно найти отрезок касательной MC. При этом мы знаем, что OC перпендикулярно MN. А значит и AK перпендикулярно MN. Какие тогда два треугольника подобны и как тогда найти KN?
Подсказка 3
Если OC и MN пересекаются в T, то выходит, что MTC и MAK подобны. При этом мы знаем их коэффициент подобия и знаем MT. Значит, мы знаем KM, а значит, так как знаем KM и MT, то знаем и KN.
Заметим сразу, что , то есть треугольник
— остроугольный. А значит
и
. Поэтому
точка
лежит снаружи треугольника
Обозначим углы треугольника за По теореме косинусов найдем угол
Проведем . Тогда
Поэтому, так как
по условию,
Пусть — точка пересечения
и
.
— биссектриса, медиана и высота в равнобедренном треугольнике
, поэтому
![]()
Тогда из прямоугольного треугольника получаем
По теореме косинусов найдем угол
По формуле половинного угла
По основному тригонометрическому тождеству
И тогда
А из треугольника находим
Ошибка.
Попробуйте повторить позже
Пусть — центр описанной окружности остроугольного треугольника
Прямая
пересекает высоты треугольника
из
точек
и
в точках
и
соответственно. Пусть
— ортоцентр треугольника
Докажите, что центр описанной окружности
треугольника
лежит на медиане треугольника
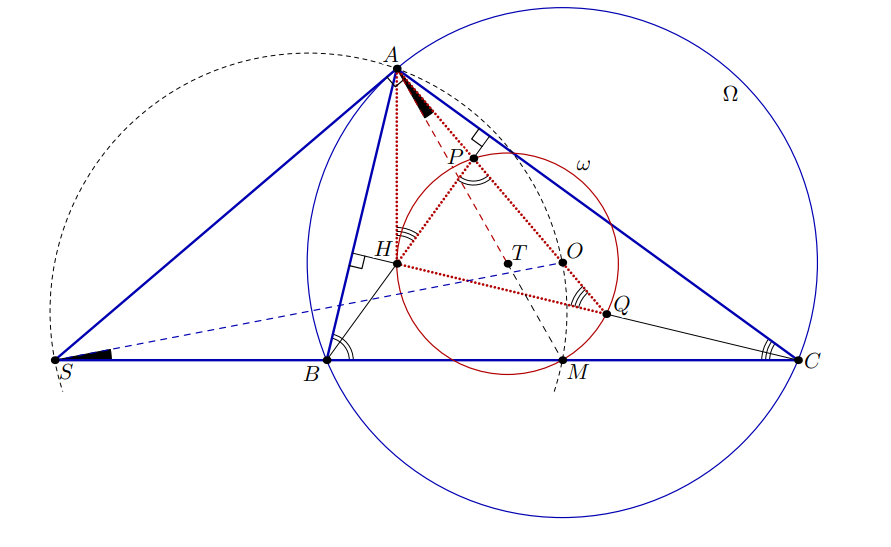
Пусть, не умаляя общности, Имеем
и аналогично
Следовательно, треугольники
и
подобны. Пусть
и
— описанные окружности треугольников
и
Поскольку
прямая
касается
Пусть — центр
и прямые
пересекаются в
Воспользуемся тем, что треугольники
и
подобны, и тем, что
касается
в
а точка
— лежит на
Рассмотрим касание
и
пусть
пересекает
в
Точки
и
соответствуют друг другу в подобных треугольниках
и
и следовательно
Следовательно
четырёхугольник
вписанный, и поскольку
имеем
Это значит, что
—
ортогональная проекция
на
которая является её серединой. Таким образом,
лежит на медиане
треугольника
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике отметили основания высот
из вершин
и
соответственно. Пусть
—
окружности, вписанные в треугольники
и
соответственно, касающиеся сторон
и
в точках
и
соответственно. Пусть прямая
вторично пересекает окружности
в точках
и
соответственно. Докажите, что
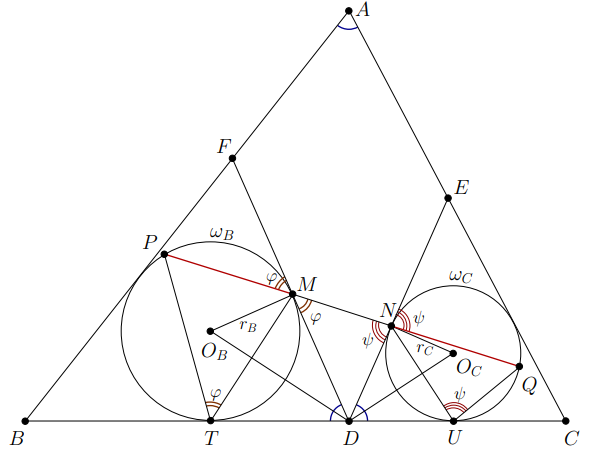
Пусть и
— центры
и
их радиусы —
и
а точки касания с
—
и
Из вписанных четырёхугольников
и
имеем:
Значит, прямоугольные треугольники и
подобны c коэффициентом
Пусть и
Прямые
и
касаются
и
откуда:
(Возможно, что точка или
совпала с
или
или лежит внутри треугольника
или
Чтобы убрать привязку к
конкретным случаям, можно использовать направленные углы)
В окружностях и
длины хорд
и
равны соответственно:
Напишем теорему синусов для треугольника
Наконец, собирая все полученные равенства:
получаем требуемое.
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике обозначили точку пересечения высот через
, центр описанной окружности через
. Площади
треугольников
и
равны 5 и 3 соответственно. Найдите площадь треугольника
.
Источники:
В точке пересекаются три высоты треугольника. Так как
— центр описанной окружности, то в точке
пересекаются серединные
перпендикуляры треугольника. Пусть точка
— середина стороны
, тогда
медиана. Точка
— точка пересечения медианы и
прямой
.
![]()
Треугольники и
подобны (следует из параллельности прямых
и
, которые обе перпендикулярны прямой
).
Так как
(это одно из свойств ортоцентра из школьной геометрии), то коэффициент подобия равен 2. Значит,
, то есть медиана
делится точкой
в отношении
. Это означает, что
- точка пересечения медиан
треугольника
. Поэтому площадь
в 2 раза больше площади
.
Так как — середина
, то
Здесь ошибкой был бы вывод о том, что, значит, . Дело в том, что выше доказано, что одна из этих трех площадей
является суммой двух других. Но какая именно, зависит от рисунка, который мы сделаем. Важно, где прямая
пересекает
стороны треугольника. Если треугольник
правильный, то точки
и
совпадают и указанные в условии задачи
три площади вырождаются (это здесь невозможно, так как дано, что площади равны 3 и 5). Если прямая
проходит
через любую вершину треугольника, то тогда одна из трех площадей равна 0 , а две другие — ненулевые, но равны между
собой (тоже не наш случай). Если же прямая
пересекает две стороны (рассмотренный выше случай), то мы доказали,
что одна из этих трех площадей (в одном случае это
, в другом —
, в третьем - OHV) является суммой двух
других.
Поэтому получаем либо (то есть
), либо
(то есть
), либо
(что невозможно).
Ошибка.
Попробуйте повторить позже
Окружности радиусов и
касаются внутренним образом в точке
. Хорда
большей окружности перпендикулярна
диаметру
меньшей окружности.
— одна из точек пересечения
с меньшей окружностью. Найти радиус окружности, описанной
около треугольника
.
Обозначим центры окружностей как и
соответственно.
Тогда .
![]()
Треугольники и
равнобедренные, пусть
и
Тогда по свойству внешнего угла треугольника
По теореме синусов в треугольнике получаем
По теореме синусов в треугольнике получаем
Теперь применим теорему синусов к треугольнику обозначив искомый радиус описанной около него окружности за
Следовательно
Ошибка.
Попробуйте повторить позже
Две окружности радиусов и
касаются прямой
в точках
и
. Пусть
— точка пересечения этих окружностей,
наиболее удалённая от
. Докажите, что радиус описанной окружности треугольника
не зависит от положения
окружностей.
![]()
Обозначим и
за
и
соответственно. Выберем на окружности радиуса
произвольную точку
По теореме об угле
между касательной и хордой
По теореме синусов для треугольника
Аналогично для другой окружности и
Теперь записываем теорему синусов для треугольника обозначив радиус описанной окружности это треугольника за
Перемножим данные равенства
Итак, не зависит от положения окружностей, он зависит только от их радиусов.
Ошибка.
Попробуйте повторить позже
Живописец закрасил акварелью полумесяц на клетчатой бумаге. Контур полумесяца состоит из двух дуг — одна от окружности с центром в
, проходящей через
, другая — от окружности с центром в
, проходящей через
. К утру краска расплылась так, что
каждая точка полумесяца превратилась в круг радиуса
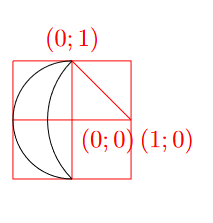
Найдите площадь получившейся фигуры.
Источники:
Подсказка 1
Когда краска расплылась, мы получили сложную фигуру, для площади которой точно не существует формулы. В таких случаях мы разбиваем фигуру на более простые, площади которых умеем вычислять.
Подсказка 2
Мы умеем находить площади окружностей, колец, секторов. Данная картинка удобно разбивается на эти фигуры или их части. При том, очевидно, что на концах нашего полумесяца нельзя брать целые окружности, потому что иначе усложняется вычисление площади остальной части фигуры. Подумайте, как можно, используя данные фигуры, разбить нашу?
Подсказка 3
Давайте разобьём фигуру на следующие части:
Пусть рисунок расплылся на радиус . К площади полумесяца прибавятся «поля», которые можно разбить на левое, правое и два
закругления на концах рогов.
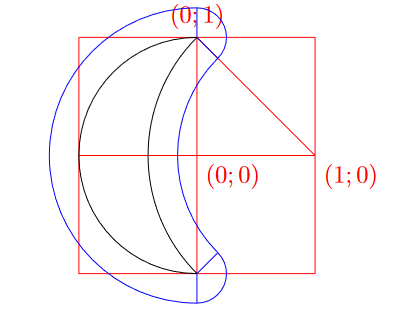
Площадь полумесяца равна половине площади круга радиуса минус сегмент круга радиуса
Площадь левого поля ”— половина от площади кольца с радиусами и
:
Площадь правого поля ”— четверть от площади кольца с радиусами и
:
Закругления на концах рогов вместе составляют три четверти окружности радиуса :
Вместе получается:
И тогда ответ:
Ошибка.
Попробуйте повторить позже
Диагонали и
трапеции
пересекаются в точке
а отношение оснований
Точки
и
— центры
окружностей
и
вписанных в треугольники
и
соответственно. Прямая, проходящая через точку
пересекает
в точках
и
а
— в точках
и
(
и
находятся ближе к
). Найдите радиус окружности
если
а
Источники:
Подсказка 1
Треугольники △AMD и △CMB подобны с коэффициентом 1/2, поэтому все соответствующие элементы относятся как 1/2. Нам дано произведение MZ*MY, которое напоминает произведение секущей на внешнюю часть. Но ведь мы знаем, что MZ/MX=1/2, поэтому легко находим MX*MY=10. А чему там равняется произведение секущей на внешнюю часть?
Подсказка 2
Конечно, квадрату отрезка касательной! Давайте отметим точку касания T: окружности ω₁ c отрезком BM. Тогда MT=√10. Если бы мы еще нашли MI₁, всё было бы в шоколаде...
Подсказка 3
Мы знаем, что MI₁/MI₂=2 и при этом MI₁+MI₂=13/2. Тогда MI₁=13/3. Воспользуйтесь теоремой Пифагора и завершите решение!
![]()
Пусть центр окружностей и
это
и
соответственно. Пусть точка
— точка касания
на
Тогда
| (1) |
Рассмотрим треугольники и
Они подобны с коэффициентом
Из этого следует, что
как
соответственные элементы в подобных треугольниках. Тогда
Используя , получаем
Пусть радиус это
тогда радиус
это
Тогда нужно найти
Рассмотрим
Из подобия и
получаем , что
из этого следует, что
Тогда
Ошибка.
Попробуйте повторить позже
В треугольнике в котором
точка
на стороне
такова, что
Точка
— середина
точки
на
стороне
и
на луче
таковы, что точки
и
лежат на одной прямой, которая параллельна
Докажите, что
Пусть — точка, симметричная точке
относительно
В четырехугольнике
диагонали пересекаются в точке
и делятся
точкой пересечения пополам, следовательно
является параллелограммом, в частности прямые
и
параллельны. Пусть
— точка, пересечения прямых
и
тогда
так же является параллелограммом, таким образом,
Аналогично,
И
Докажем, что Действительно, из подобия треугольников
и
следует равенство отношений
Аналогично
Наконец, из равенств и
следует равенство отношений
следовательно,
что
влечет
![]()
Наконец, точка лежит на серединном перпендикуляре к отрезку
поскольку
Пусть
— середина
тогда
то есть
так же является серединой отрезка
следовательно, серединные
перпендикуляры к отрезкам
и
совпадают, значит
лежит на серединном перпендикуляре к
что завершает
доказательство.
Ошибка.
Попробуйте повторить позже
Пусть — биссектриса треугольника
точки
— центры вписанных окружностей треугольников
и
соответственно. Прямая
пересекает прямую
в точке
Докажите, что
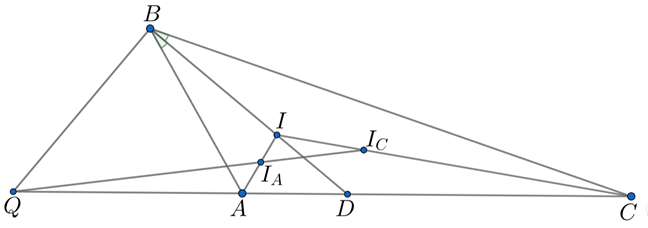
Прямые и
пересекаются в центре
вписанной окружности треугольника
При этом
По теореме
Менелая
Следовательно, — внешняя биссектриса угла
что и требовалось.
Ошибка.
Попробуйте повторить позже
[Для 8 класса] Внутри треугольника отмечена точка
так, что
Прямая
пересекает сторону
в точке
Оказалось, что
Докажите, что
Отметим на отрезке такую точку
что
Тогда равенство из условия задачи можно записать в виде
откуда и треугольники
и
подобны. Но треугольники
и
равны, значит,
значит,
треугольник
равнобедренный, а вместе с ним и треугольник
равнобедренный.
Ошибка.
Попробуйте повторить позже
Окружность с центром в точке
на стороне
треугольника
касается сторон
и
в точках
и
соответственно.
Известно, что
, а угол
равен
. Найти углы треугольника
и отношение его площади к площади круга,
ограниченного окружностью
Подсказка 1
Давайте будем думать, как нам считать и что через что выражается. Сразу понятно, что если нам дан угол EOD, то и угол B нам также дан. При этом, если у нас были бы известны углы C и A, то крайне понятно считались бы оба прямоугольных треугольника AOD и COE. Что нам это дает, для нахождения углов? Как мы можем их между собой связать?
Подсказка 2
Мы могли бы связать углы A и С, так как в прямоугольных треугольниках две стороны равны как радиусы, а отношение двух других равно константе. При этом, есть еще одна связь, что сумма углов A и С равна заданному углу DOE. Значит, мы найдем углы A и C. Как теперь можно найти отношение площадей круга и треугольника, если уже известны углы, а значит и радиус и стороны треугольника ABC?
Подсказка 3
Верно, к примеру, мы можем расписать через sin(DOE/2) и cos(DOE/2) отрезок DE, так как треугольник DOE - равнобедренный(т.синусов и опустить высоту, к-ая будет и медианой). Значит, мы через известный нам котангенс, выразим котангенс от половины такого же угла, а после этого сможем явно написать чему равны отрезки BD, BE и OE(последнее - радиус), а значит, найдем окружность. Правда ли, что теперь у нас осталось выразить только отрезки CE и AD и площадь треугольника также будет найдена?
Подсказка 4
Ну конечно, ведь тогда мы найдем обе стороны нашего треугольника и угол между ними. А значит и площадь. Как их найти? Так у нас же есть радиус и углы в прямоугольных треугольниках. Значит, мы сможем, все что нужно найти. Остается только посчитать :)
![]()
Обозначим
Так как , то
Из прямоугольных
и
находим
Так как и
— радиус окружности
Так как , то получаем
, т. е.
Так как угол острый как угол прямоугольного
Из равнобедренных и
находим
Отсюда
Тогда площадь равна
И искомое отношение равно
Ошибка.
Попробуйте повторить позже
Длина стороны четырехугольника
вписанного в окружность равна 5 . Точка
делит эту сторону в отношении
, а прямые
и
параллельны сторонам
и
соответственно. Найти длину стороны
четырехугольника.
Подсказка 1
Сразу обозначим все углы, вытекающие из параллельности. Как использовать отношение, данное в условии? Какую связь можно заметить между треугольниками на картинке?
![]()
Прямые и
параллельны, поэтому углы
и
равны (обозначены на рисунке цифрой 2 ), аналогично равны углы
и
(обозначены на рисунке цифрой 3). Отсюда следует подобие треугольников
и
с коэффициентом подобия 4 и
равенство углов
и
(обозначены на рисунке цифрой 1). Заметим, что
.
Покажем, что треугольник подобен треугольникам
и
, вершины треугольников перечислены в порядке
соответствия. Углы
и
, полученные при пересечении прямой
параллельными прямыми
и
, равны как
внутренние накрест лежащие. Сумма углов
и
равна
, как сумма противоположных углов
вписанного в окружность четырёхугольника. Значит, угол
и треугольник
подобен треугольникам
и
.
Положим и
, тогда
и
. Треугольники
и
подобны с коэффициентом подобия
, и
стороны
и
треугольника
соответствуют сторонам
и
треугольника
, поэтому
. Значит,
и, треугольники
и
подобны с коэффициентом подобия 2. Следовательно, сторона
в два раза длиннее стороны
, т.е.
длина стороны
равна 2.
Ошибка.
Попробуйте повторить позже
Дан треугольник . Пусть
— середина стороны
— проекция вершины
на биссектрису угла
— проекция
вершины
на биссектрису угла
Обозначим через
центр описанной окружности треугольника
Аналогично
определены точки
Докажите, что ортоцентр треугольника
совпадает с центром вписанной окружности треугольника
Пусть описанная окружность треугольника является единичной с центром в нуле, и треугольник
положительно ориентирован.
Обозначим через
комплексное число, отвечающее повороту на
против часовой стрелки, через
— отвечающее повороту на
по часовой стрелке. Тогда центр вписанной окружности имеет координату
Обозначим середины дуг
через
и
соответственно. Тогда
Поскольку
является является проекцией на хорду
получаем
Аналогично
Легко проверить, что откуда угол
(как ориентированные). Значит,
откуда
Аналогично Таким образом
Последнее выражение является чисто мнимым, откуда заключаем, что Тогда и
что и
требовалось доказать.
Ошибка.
Попробуйте повторить позже
На сторонах и
остроугольного треугольника
выбраны точки
и
соответственно так, что
проходит через центр
описанной окружности треугольника
Обозначим через
и
середины отрезков
и
соответственно. Докажите, что
Пусть описанная окружность треугольника является единичной с центром в
и треугольник
положительно ориентирован.
Точка
лежит на прямой
откуда
то есть
Выразим координату точки
через
Во-первых,
Также
Из последних двух уравнений находим
Теперь
Заметим, что Тогда
Итого Осталось проверить, что
равно своему сопряженному, что сразу следует из доказанного
выше.
Ошибка.
Попробуйте повторить позже
Докажите, что где
— центр описанной окружности треугольника
— ее радиус,
— центр вневписанной
окружности, касающейся стороны
— радиус этой окружности.
Пусть описанная окружность треугольника является единичной с центром в нуле, а также треугольник
положительно
ориентирован. Пусть
— комплексное число с единичным модулем, такое, что
попадает в середину дуги
и
попадает в точку
аналогично определим число
(
— середина дуги
,
совпадает с
). Тогда середина дуги
имеет координату
Центр вписанной окружности имеет координату
Середина дуги
является срединой отрезка между центром
вписанной окружности и
откуда точка
имеет координату
Проекция
на сторону
имеет координату
Тогда
При этом модуль этого комплексного числа равен Тогда
(так как
).
При этом
Откуда (так как
). Таким образом,
то есть
что и
требовалось.
Ошибка.
Попробуйте повторить позже
(a) Пусть описанная окружность четырехугольника является единичной с центром в нуле. Обозначим через ортоцентр треугольника
Аналогично определим точки
Заметим, что
Нам надо
проверить вещественность двойного отношения
что верно, поскольку
лежат на одной
окружности.
(b) Рассмотрим треугольник с вершинами Заметим, что
то есть этот
треугольник просто равен треугольнику
а следовательно, равны и их описанные окружности.
Ошибка.
Попробуйте повторить позже
Остроугольный треугольник вписан в окружность
с центром в точке
Прямая
параллельная прямой
пересекает
отрезки
и луч
в точках
и
соответственно. Докажите, что центр окружности, описанной около треугольника
середина отрезка
и точка
лежат на одной прямой.
Пусть описанная окружность треугольника является единичной с центром в
Зафиксируем на отрезке
точку
Тогда
откуда
Найдем координату точки
Во-первых,
откуда
то есть
При этом
лежит на
откуда
Решая систему на
и
находим
Аналогично координата точки вычисляется по формуле
Тогда координата середины отрезка
вычисляется по формуле
Обозначим через центр описанной окружности треугольника
Заметим, что треугольники
и
подобны и
одинаково ориентированы, откуда
откуда
Нам осталось проверить, что отношение вещественное, что сразу следует из подстановки
Ошибка.
Попробуйте повторить позже
В неравнобедренном остроугольном треугольнике точки
и
— середины сторон
и
соответственно,
— центр
описанной окружности,
— точка пересечения высот. Прямые
и
пересекаются в точке
а прямые
и
— в точке
Оказалось, что четырёхугольник
— ромб. Докажите, что точки
и
лежат на одной
прямой.
Как обычно будем считать описанную окружность треугольника с центром в
Точка
лежит на одной прямой с
откуда
откуда
При этом
откуда
Подставляя
из первого уравнения, находим
Аналогично
Заметим, что
и
откуда четырёхугольник
— параллелограмм. Значит,
условие того, что
— ромб равносильно тому, что
то есть
Раскрыв скобки в последнем равенстве, получаем
Первая скобка равна быть не может, поскольку иначе
что означало бы, что треугольник
— равнобедренный с
основанием
Значит,
Проверим, что отношение
равно своему сопряженному. Имеем
С другой стороны
Наконец, равенство следует из того, что
Ошибка.
Попробуйте повторить позже
Пусть — основания высот треугольника
из вершин
соответственно. обозначим через
проекции точки
на прямые
и
соответственно. Аналогично определим точки
Докажите, что
Расположим систему отсчета так, чтобы описанная окружность треугольника была единичной с центром в нуле. Заметим, что
является проекцией
на хорду
Тогда
Аналогично
Получаем, что
Вспоминая, что
получаем
Аналогично
У трех полученных выражений общий множитель а также
откуда
получаем требуемое.



