Ошибка.
Попробуйте повторить позже
В выпуклом четырёхугольнике углы
и
равны. Докажите, что
Предположим, что прямые и
пересекаются в точке
Тогда треугольник
— равнобедренный, откуда следует, что
(это не зависит от того, с какой стороны пересекаются прямые
и
). По неравенству
треугольника получаем, что
Осталось разобрать случай параллельности
и
В этом случае углы
и
равны по
Опустим перпендикуляр
на прямую
Тогда
что и требовалось
доказать.
Ошибка.
Попробуйте повторить позже
В треугольнике взята произвольная точка
Докажите, что
Продлим до пересечения с
в точке
Заметим, что
потому что
и
Аналогично
Следовательно,
Ошибка.
Попробуйте повторить позже
Докажите, что в любой трапеции разность длин боковых сторон меньше разности длин оснований.
Отметим на такую точку
что
Получили параллелограмм
То есть
и
По
неравенству для треугольника
имеем:
(пусть не умаляя общности
). Осталось заметить, что
и
Получили требуемое. Для трапеции, у которой тупые углы не при одном основании, работает
аналогичное построение.
Ошибка.
Попробуйте повторить позже
Докажите, что для любого прямоугольника сумма расстояний от произвольной точки плоскости до трех его вершин больше расстояния от этой точки до четвертой вершины.
Заметим, что по неравенству треугольника
Также
по неравенству треугольника
Осталось
заметить, что
что и требовалось.
Ошибка.
Попробуйте повторить позже
В треугольнике отметили точку
на отрезке
Докажите, что
меньше хотя бы одного из отрезков
и
Предположим противное, пусть и
Как известно, в треугольнике против большей стороны лежит больший
угол. Получается, что
и
Если сложить неравенства, то получим, что
пришли к противоречию.
Ошибка.
Попробуйте повторить позже
На сторонах и
треугольника
выбраны точки
и
соответственно, так что
Докажите, что из отрезков
и
можно составить треугольник.
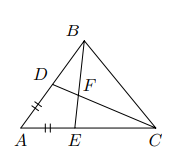
Достаточно проверить выполнение трех неравенств треугольника. Пусть — точка пересечения отрезков
и
Очевидно,
Проверим второе неравенство треугольника: Для этого прибавим к частям этого неравенства равные отрезки
и
т. е. проверим, что
Действительно, по неравенству треугольника
и
кроме того,
Значит,
что и требовалось.
Аналогично доказывается третье неравенство треугольника
Ошибка.
Попробуйте повторить позже
В четырёхугольнике углы
и
— не острые. На сторонах
и
отмечены точки
и
соответственно.
Докажите, что периметр четырёхугольника
не меньше удвоенной длины диагонали
Подсказка 1
Попробуем доказать, что отрезок, соединяющий середины противоположных сторон, не больше полусуммы противоположных сторон!
Лемма. Пусть и
— середины сторон
и
четырехугольника
. Тогда
Доказательство. Пусть — середина диагонали
Тогда
По неравенству треугольника для
треугольника
имеем:
после подстановки полученных равенств:
что завершает доказательство.
Вернемся к решению задачи. Пусть и
— середины сторон
и
По лемме
Ясно, что длина
медианы, проведенной из вершины при неостром угле, не превосходит половины стороны, к котором она проведена, следовательно
и
Осталось заметить, что по неравенству ломанной верно неравенство
Подставляя полученные неравенства имеем
домножив данное неравенство на получим требуемое.
Ошибка.
Попробуйте повторить позже
Дан треугольник в котором
Внутри этого треугольника отмечены точки
и
такие, что
и
Докажите, что
Подсказка 1
Хотим оценить сумму - так попробуем оценить каждый ее член! Какие неравенства можно к ним применить?
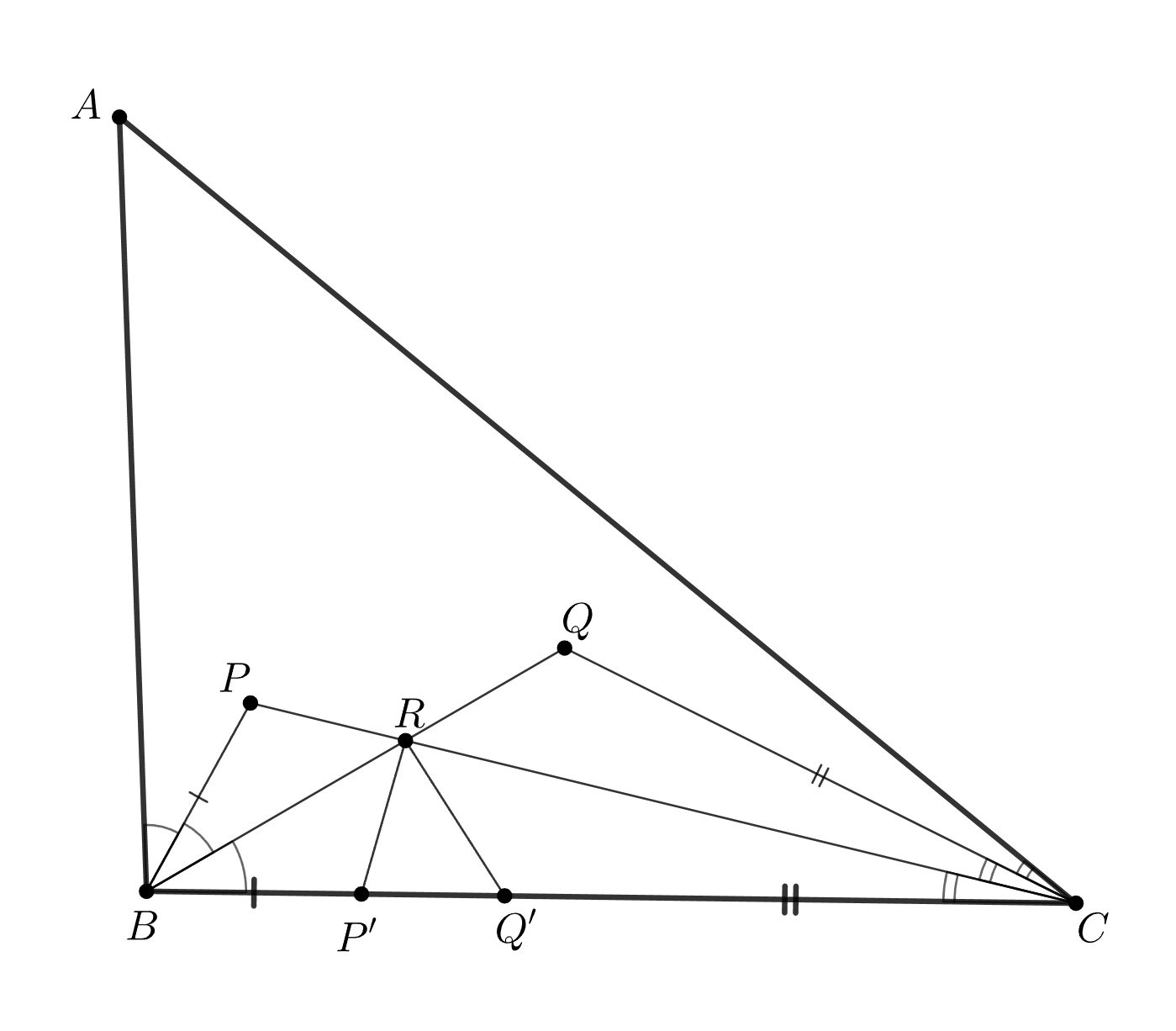
По неравенству треугольника для треугольника имеем:
Аналогично
Складывая полученные неравенства имеем
Осталось показать, что Пусть
— точка пересечения прямых
и
— образ точки
при симметрии
относительно прямой
— образ точки
при симметрии относительно прямой
Тогда достаточно показать, что
что эквивалентно
Пусть Тогда
Таким образом, неравенство (*) имеет вид
Наконец,
что верно, т.к.
Ошибка.
Попробуйте повторить позже
(a) Пусть и
– положения конца минутных стрелок часов с номером
в моменты
и
минут,
– центр
-х часов, а
– центр стола.
Лемма. для любого
Доказательство. Рассмотрим треугольник с вершинами Ясно, что
– его медиана. Как известно, медиана треугольника
не превосходит полусуммы прилежащих к ней сторон (достаточно достроить треугольник до параллелограмма
и применить
неравенство треугольника к
).
Понятно, что можно подобрать так, чтобы для некоторого
точки
и
не лежали на прямой
т. е. по крайней мере одно
из
неравенств становится строгим. Сложим все эти неравенства, получим
Ясно, что в таком случае либо либо
Тогда сумма расстояний от центра стола до концов минутных стрелок будет гарантированно больше,
чем сумма расстояний до центров часов либо в момент
, либо в момент
(b) Зафиксируем момент времени 0 – начало отсчета. Рассмотрим произвольные часы (с номером ). Из леммы в пункте
), в
частности, следует, что среднее за один час расстояние от конца минутной стрелки до
строго больше
Докажем, что
существует момент времени
такой, что для любого
среднее расстояние от конца минутной стрелки до
за
время от 0 до
больше, чем
Пусть
– время, которое занимает один полный оборот
-ых часов. Введем еще
переменную
Пусть
– разность между средним расстоянием от конца минутной стрелки до
за один
полный оборот и
(по замечанию,
). И, наконец, пусть
есть среднее расстояние от конца минутной стрелки
до
за время от 0 до
Нетрудно понять, что
ограничено снизу одной и той же константой для всех
Обозначим ее как
(при этом
вполне может быть отрицательным). Например, по
неравенству треугольника ясно, что
длины минутной стрелки, поэтому
больше либо равно, чем
С помощью введенных обозначений, легко выразить разность между средним расстоянием за время от 0 до от конца минутной стрелки
до
и
для произвольного
Объясним эту формулу. Разобьем время на максимальное число полных оборотов (
) и то что осталось – интервал от
до
Поскольку
– разность между средним расстоянием от конца минутной стрелки до
за один оборот часов и
то за
оборотов средняя разность будет равна
а суммарная разность
. Ясно, что среднее расстояние от конца минутной
стрелки до
за время от 0 до
равно среднему расстоянию за время от
до
поэтому средняя
разность расстояния от конца минутной стрелки до
и
за это время равно
а суммарное –
Итак, в числителе стоит суммарная разность за время
и ее мы делим на
чтобы получить
среднюю.
Поскольку по замечанию второе слагаемое в числителе ограничено снизу. А значит, если
является
достаточно большим числом, то первое слагаемое будет больше второго по модулю, и числитель будет являться положительным числом.
Именно это и необходимо, чтобы среднее расстояние за время от 0 до
от конца минутной стрелки до
было больше
Вернемся к нескольким часам. Выберем наибольшее из всех и обозначим его
Рассмотрим теперь разность суммы расстояний от
концов минутных стрелок всех часов до
и
Рассмотрим среднее этой величины за время
. Оно является суммой по
всем
разности между средним расстоянием (за время
) от конца стрелки до
и
По выбору
все слагаемые этой суммы
положительные. Итак, у нас есть некоторая величина, среднее значение которой положительно – значит и в некоторой точке значение
этой величины положительно. Эта некоторая точка и является моментом времени, в котором сумма расстояний от концов
минутных стрелок до центра стола больше, чем сумма расстояний от центров часов до центра стола. Именно это и требовалось
получить.
Ошибка.
Попробуйте повторить позже
Точки и
делят сторону
треугольника
на три равные части. Докажите, что
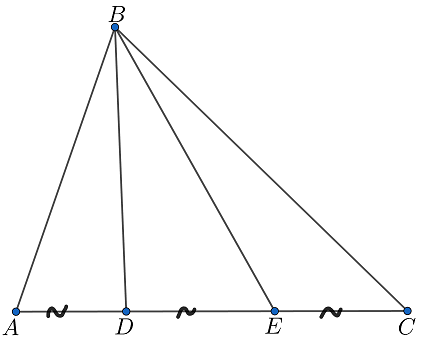
Вспомним известное неравенство. В треугольнике медиана меньше полусуммы сторон, к которым она не проведена. Чтобы его доказать, надо просто удвоить эту медиану и написать неравенство треугольника.
Теперь к задаче. Применим это неравенство к медианам и
треугольников
и
Осталось сложить эти неравенства и получить требуемое.
Ошибка.
Попробуйте повторить позже
Точка лежит внутри острого угла. Постройте на сторонах этого угла точки
и
, для которых периметр треугольника
был
бы наименьшим.
Обозначим вершину угла через . Отразим точку
относительно сторон угла, обозначив полученные две точки через
и
.
![]()
Рассмотрим произвольные точки и
на сторонах угла. Заметим, что в силу симметрии
,
. Поэтому
периметр треугольника
равен длине ломаной
. Длина этой ломаной не меньше длины отрезка
, и
равенство возможно только когда точки
и
лежат на отрезке
. Поэтому в качестве точек
и
таких,
чтобы периметр треугольника
был наименьшим, необходимо выбрать точки пересечения отрезка
со сторонами
угла.
_________________________________________________________________________________________________________________________________________________________________________________
Замечание.
Условие, что исходный угол острый, важно: если бы был тупым, то построенный отрезок
не пересекался бы со сторонами угла,
а если бы
был прямым, то пересекался бы в точке
. В качестве упражнения докажите, что в обоих этих случаях в качестве точек
и
необходимо выбрать точку
, таким образом, периметр вырожденного треугольника
является наименьшим из
возможных.
Ошибка.
Попробуйте повторить позже
На окружности диаметра 2 выбраны точек
,
, …,
. Докажите, что на окружности можно выбрать точку
так,
что
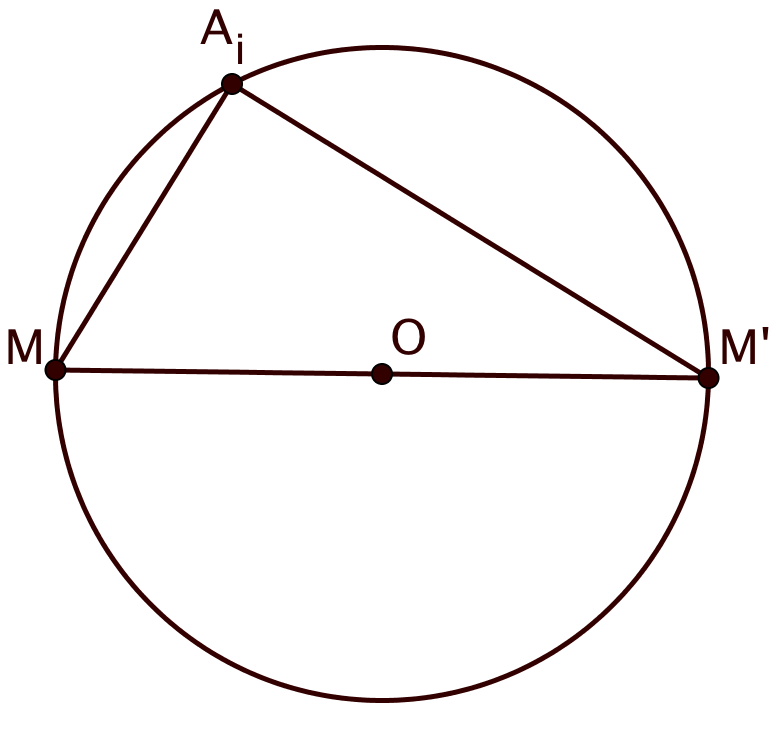
Выберем точку на окружности, и отметим также диаметрально противоположную ей точку
, причем отметим
так, чтобы ни
, ни
не совпадала ни с одной из отмеченных ранее точек
(так можно сделать, ведь на окружности отмечено лишь конечное
число точек, то есть конечное число запретов, меж тем как в качестве
мы можем выбрать любую из бесконечного числа
точек).
Для одной из выбранный точек рассмотрим два отрезка
и
. Заметим, что по неравенству треугольника
сумма
, так как
— диаметр окружности. Запишем аналогичные неравенства для всех
и сложим их. Получим
неравенство
значит, одна из двух скобок в левой части больше Таким образом, в качестве искомой точки подойдет либо
, либо диаметрально
противоположная ей точка
.
Ошибка.
Попробуйте повторить позже
Докажите, что в параллелограмме против большего угла лежит большая диагональ.
Обозначим параллелограмм через , и пусть
. Продлим отрезок
за точку
на свою длину, обозначим
полученную точку через
. Тогда
, и
. Значит,
— тоже параллелограмм, в частности,
. Так как
, а их сумма равна
, то
. Поэтому, если провести через
серединный
перпендикуляр к
, то относительно этого серединного перпендикуляра точки
и
лежат по разные стороны. Отсюда
Ошибка.
Попробуйте повторить позже
Докажите, что медиана меньше полусуммы сторон, между которыми она заключена.
Сделаем с медианой самое естественное, что можно сделать: продлим на свою длину. Обозначим получившуюся точку через . Тогда
— параллелограмм, так как его диагонали делятся точкой пересечения пополам. Значит,
. При этом по неравенству
треугольника
Замечание. Вообще, те же рассуждения можно записать через векторы. На самом деле как раз из рассуждений выше следует, что
Ошибка.
Попробуйте повторить позже
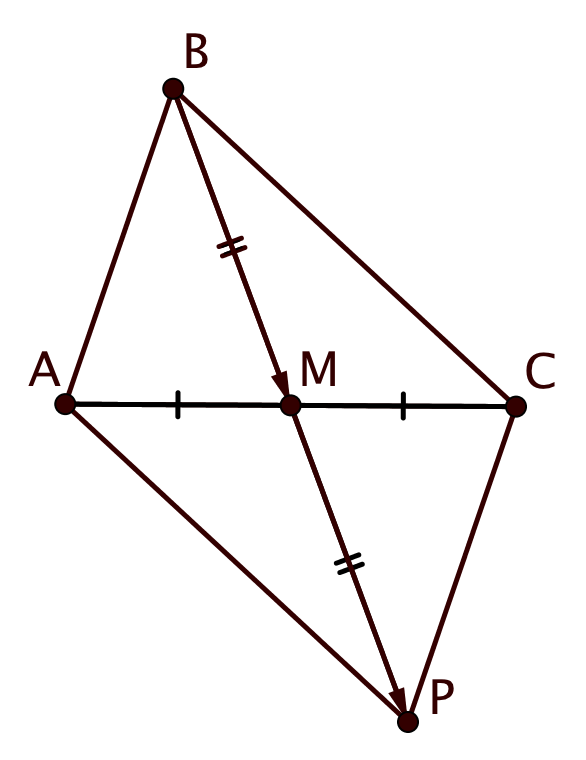
В треугольнике на стороне
выбраны точки
и
так, что
а на стороне
— точки
и
так, что
Докажите, что
Подсказка 1
Давайте обратим внимание на схожесть расположения каждого из отрезков нашего неравенства. Каждый из них включен в треугольник с вершиной B. Попробуйте выразить вектора AC, KN и LM через вектора выходящие из вершины B.
Подсказка 2
Не просто же так в условии сказано, что BL=KA, а BM=NC. Подумайте, почему эти же равенства будут верны и в векторном виде и подставьте их в выражения, которые мы находили ранее. Подумайте, как теперь мы можем связать вектора AC, KN и LM.
Подсказка 3
Если до этого вы всё сделали правильно, то должны были получится векторные равенства: KN = BN - BK, LM = NC - KA. Если сложить два векторных равенства, то получим KN+LM=(BN+NC)-(BK+KA)=BC-BA=AC. Подумайте, почему данное векторное равенство доказывает неравенство из условия.
Рассмотрим для определенности конфигурацию, изображенную на рисунке
![]()
Тогда имеем следующие равенства:
Поскольку а
то сложив второе и третье равенства получим
Следовательно
Заметим, что при таком решении не существенно, как расположены точки и
Ошибка.
Попробуйте повторить позже
В равнобедренной трапеции проведена диагональ. По контуру каждого из получившихся двух треугольников ползёт свой жук. Скорости движения жуков постоянны и одинаковы. Жуки не меняют направления обхода своих контуров и по диагонали трапеции они ползут в разных направлениях. Докажите, что при любых начальных положениях жуков они когда-нибудь встретятся.
Источники:
Подсказка 1
Можно изобразить трапецию и задать направления жучкам. Понятно, что хочется, чтобы жучки встретились на AC. А что происходит с жучками, когда один из них проходит целый круг?
Пусть в равнобедренной трапеции с основаниями
проведена диагональ
так что первый жук ползает по циклу
второй — по циклу
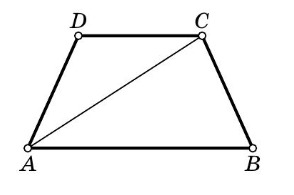
Рассмотрим моменты времени, в которые первый жук оказывается в точке За время обхода первым жуком полного цикла из
снова в
второй жук сдвигается по своему циклу на
в одну и ту же сторону. Поскольку
при таких сдвигах в один из рассматриваемых моментов времени второй жук окажется на расстоянии меньше до точки
по ходу
своего движения, а значит, встретится с первым жуком на диагонали
Ошибка.
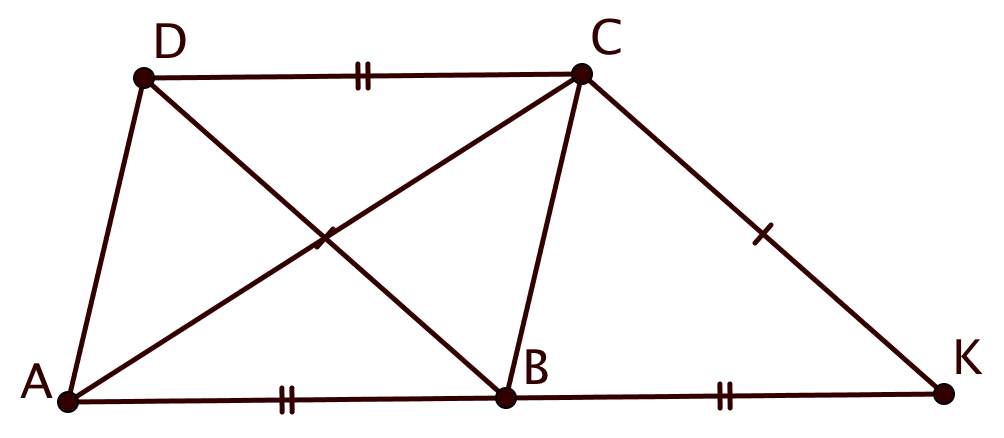
Попробуйте повторить позже
На диагонали выпуклого четырехугольника
отмечена точка
. Известно, что
u
. Докажите, что
.
![]()
Отметим на отрезке точки
и
так, что
, чтобы получить
и
. Причём как внешние
углы
и
. Следовательно, треугольник
правильный, а тогда
. Так как
, то получаем, что точка
совпадает с
, поэтому
. Кроме того,
, как гипотенуза и меньший катет
прямоугольного треугольника с углом
. Итак,
по неравенству треугольника, что и
требовалось.
Ошибка.
Попробуйте повторить позже
В равнобедренном треугольнике
и
Докажите, что
.
Подсказка 1
Угол в 20 градусов — так себе угол, нам больше нравятся углы в 30, 45, 60 или 90 градусов.. Как бы из угла 20 градусов сделать один из этих углов?
Подсказка 2
Давайте попробуем сделать угол в 60 градусов! Для этого отсимметричим треугольник АВС относительно ВС, а потом еще раз, относительно новой полученной стороны! Вспоминаем, что известно про треугольники с углом 60
Подсказка 3
Хм, теперь из оснований равнобедренного треугольника образовалась ломаная! Что бы с ней сделать...
Повернём вокруг точки
против часовой стрелки на 20 градусов, получим
. Сделаем такой же поворот для
,
получим
.
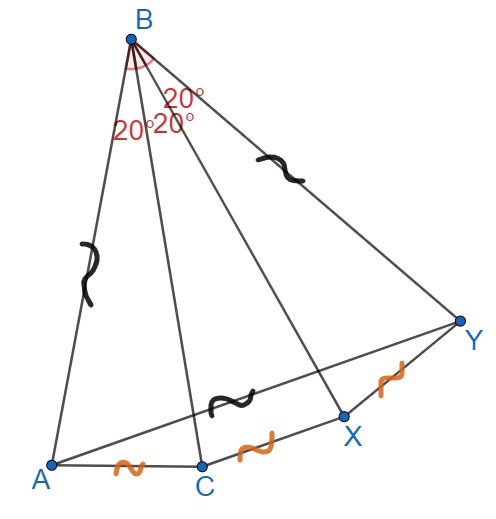
Заметим, что — равносторонний. Запишем неравенство для ломаной
:
Ошибка.
Попробуйте повторить позже
Внутри прямого угла с вершиной взята точка
, а на его сторонах — точки
и
. Докажите, что
Подсказка 1
Так, снова встречаем неравенство на странные отрезки, которые между собой никак не соотносятся. Мы знаем несколько известных неравенств на отрезки - например, неравенство треугольника. Тогда попробуем его здесь найти и использовать
Подсказка 2
Для этого нам пригодится создать на картинке отрезок длинной 2ОС, пока его нет. Давайте просто продлим за точку О отрезок ОС до точки ОС1, так, что ОС1 = ОС. Теперь длина СС1 = 2ОС. Ищем треугольник, для которого можно написать неравенство! (мы же предварительно нарисовали картинку и отметили там все отрезки, о которых идет речь, да?)
Подсказка 3
Например, можно для треугольника АСС1. То есть, если мы докажем, что АС1<= АВ + ВС, то получим неравенство из условия! Осталось это доказать, и задача решена😏
Первое решение.
![]()
Удвоим отрезок за точку
и получим отрезок
длины как в левой части искомого неравенства. Нужно доказать, что его
длина меньше периметра треугольника
.
Отразим также точку относительно точки
и обозначим полученную точку за
. В силу осевой симметрии точек
и
относительно
получаем
. Из равенства треугольников
и
по двум сторонам (из построения) и углу между
ними (как вертикальные) имеем
. Наконец, из неравенства ломаной
получаем
требуемое.
Замечание. Точки необязательно лежат на одной прямой.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
![]()
Отразим точку относительно сторон угла
, получим точки
и
.
По построению стороны угла являются серединными перпендикулярами к сторонам и
, а в силу того, что угол между
сторонами угла прямой, угол
между перпендикулярами к ним тоже является прямым. Поэтому точка
лежит на
гипотенузе
треугольника
и является центром описанной около него окружности, а отрезок
— её радиусом
.
Выражение в правой части неравенства превращается в длину ломаной , которая больше длины отрезка
______________________________________________________________________________________________________________________________________________________
Третье решение
Используем прямоугольный треугольник пусть
— середина
, тогда
. В связи с этим нужно доказать
![]()
Запишем неравенство треугольника для :
. Осталось доказать
. Но это известное неравенство
медианы, применённое для
.
В итоге
Ошибка.
Попробуйте повторить позже
Точки и
делят сторону
треугольника
на три равные части. Докажите, что
.
Подсказка 1
Заметим, что у нас есть несколько треугольников на картинке и несколько проведенных в них медиан (например, CD - медиана ACE.) Как мы можем этим воспользоваться для доказательства неравенств?
Подсказка 2
Да, при наличии медианы мы всегда можем вспомнить о неравенство на стороны треугольника и медиану! Например, 2CD < AC + CE. Попробуйте, используя такие неравенства для имеющихся треугольников, теперь доказать требуемое в задаче.
![]()
Запишем для треугольника неравенство на медиану:
Точно такое же неравенство можно написать для треугольника :
Сложим эти два неравенства:



