Ошибка.
Попробуйте повторить позже
Четырёхугольник вписан в окружность
с центром
причём
не лежит на диагоналях четырёхугольника. Описанная
окружность
треугольника
проходит через середину диагонали
Докажите, что описанная окружность
треугольника
проходит через середину диагонали
Источники:
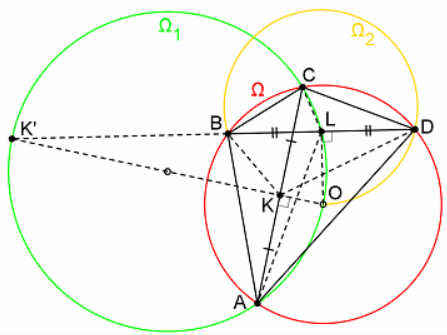
Отметим точки и
– середины диагоналей
и
Сделаем инверсию относительно окружности
Окружность
переходит
в прямую
а значит точка
переходит в точку пересечения
и
–
Отметим
– точку пересечения прямых
и
Для того, чтобы доказать, что точка
лежит на окружности
достаточно проверить, что точки
и
также инверсны относительно окружности
ведь под действием такой инверсии прямая
переходит в окружность
Отметим, что четырехугольник
вписанный, ведь
По свойству степени точки
где
– радиус
По определению это означает, что точки
и
инверсны относительно
Ошибка.
Попробуйте повторить позже
Геометрическая прогрессия состоит из натуральных чисел. Первый и последний члены прогрессии взаимно просты. Докажите, что
-й
член прогрессии является
-й степенью натурального числа.
Пусть наша прогрессия а знаменатель
Так как
— натуральные числа, значит,
— рациональное число, пусть
где
и
По условию первый и
члены взаимно просты. Значит
Так
как
— натуральное, а
то
Если
то
следовательно
Теперь ясно, что
— получили требуемое.
Ошибка.
Попробуйте повторить позже
На сторонах и
ромба
отмечены точки
и
соответственно так, что
Докажите, что точка пересечения
медиан треугольника
лежит на диагонали
ромба.
Источники:
.png)
Первое решение. Пусть точки и
будут двигаться линейно из точки
в точку
и из точки
в точку
с равными
скоростями. Тогда точка
— середина отрезка
также будет двигаться линейно. Значит, и точка
делящая отрезок
в
отношении
к
будет двигаться линейно. Следовательно, точка пересечения медиан треугольника
движется линейно по
некоторой прямой
Осталось показать, что
Для этого достаточно найти два момента времени, когда точка пересечения медиан
лежит на
Например, подойдут положения
и
Второе решение. Расположим наш ромб на комплексной плоскости так, чтобы его центр попал в начало отсчета, вершина
— в точку
вершина
— в точку
(этого можно добиться с помощью поворота, параллельного переноса и
гомотетии). Тогда вершины
и
попадут на вещественную ось, причем
Пусть
откуда
Аналогично
Координата точки пересения медиан треугольника
может быть вычислена по формуле
Последнее выражение является чисто мнимым, а значит, лежит на прямой
Ошибка.
Попробуйте повторить позже
Углы и
совмещаются поворотом так, что луч
совмещается с лучом
а луч
— с
В них вписаны
окружности, пересекающиеся в точках
и
Докажите, что углы
и
равны.
Источники:
Подсказка 1
У нас на картинке есть две вписанные окружности. Было бы полезно отметить их центры O₁ и O₂. Верно ли, что теперь можно доказывать равенство уголков ∠O₁OF и ∠O₂OE?
Подсказка 2
Верно! Ведь ∠AOF и ∠DOE равны. Но тогда интересно будет посмотреть на биссектрису угла ∠O₁OO₂: обозначим за OK- биссектрису в треугольнике △O₁OO₂. Тогда ∠O₁OF=∠O₂OE ⇔ ∠FOK=∠FOE. А что можно сказать про отрезки EK и FK?
Подсказка 3
Они равны, ведь O₁O₂- серпер к EF. Если бы точки O, E, K и F лежали на одной окружности, то все было бы замечательно. Какую мы знаем окружность, которая проходит через O и K...
Подсказка 4
Окружность Аполлония для точек O₁ и O₂. Осталось только доказать, что EO₁ /EO₂=FO₁ /FO₂=OO₁ /OO₂. Первое равенство очевидно, ведь EO₁=FO₁=R₁ и EO₂=FO₂=R₂. Как доказать, что OO₁/OO₂=R₁/R₂?
Подсказка 5
Нужно всего лишь посмотреть на синусы углов ∠AOO₁ и ∠COO₂!
Первое решение.
Пусть — центры окружностей,
— их радиусы. Проведём биссектрису угла
(она же — биссектриса угла
Пусть она пересекает отрезок
в точке
Поскольку
то точки принадлежат одной и той же окружности Аполлония точек
и
Поскольку
— серединный
перпендикуляр к
то равны хорды этой окружности
и
Значит, равны и опирающиеся на них вписанные углы
и
откуда немедленно следует равенство углов
и
Второе решение.
Сделаем инверсию с центром в точке такую, что первая окружность переходит в равную второй. Вторая, соответственно, перейдёт в
равную первой. Тогда, с одной стороны, лучи
и
перейдут в себя, с другой — мы имеем картинку, симметричную исходной
относительно биссектрисы угла
а значит, она же биссектриса угла
откуда
Ошибка.
Попробуйте повторить позже
Дан треугольник В нём
— точка пересечения высот,
— центр вписанной окружности,
— центр описанной окружности,
— точка касания вписанной окружности со стороной
Известно, что отрезки
и
параллельны. Докажите, что отрезки
и
также параллельны.
Источники:
Подсказка 1
Для начала, надо понять, что именно нам нужно доказывать, надо разбить нашу задачу на подзадачи, каждая из которых будет легче данной. Мы видим здесь ортоцентр и центр вписанной окружности. Из свойств ортоцентра, мы знаем, что расстояние от вершины до ортоцентра в два раза больше расстояния от центра описанной окружности до , противоположной этой вершине, стороны. Значит, стоит отметить середину BC и посмотреть, что это даст, учитывая условия задачи.
Подсказка 3
Высота из другой точки - точки I - это точка касания вписанной окружности. Значит, IK1=OM1(где К1-точка касания вписанной окружности со стороной BC). Но при этом, мы знаем, что OM1=AH/2, значит 2*IK1=AH. Где можно на картинке найти удвоенный отрезок IK1(радиус окружности)? Что это дает?
Подсказка 4
Удвоенный радиус вписанной окружности это, по сути, диаметр вписанной окружности. Значит, удобнее всего здесь отметить на этой окружности точку, диаметрально противоположную K1(искушенные читатели знают, что это совсем не простая точка).Пусть это точка D. Что тогда можно сказать про эту точку и точку А? В какой точке пересекает отрезок DA сторону BC? А если провести прямую, параллельную BC и проходящую через D?
Подсказка 5
Если провести такую прямую, то, во-первых, она будет касательной к вписанной окружности. Но при этом для треугольника, который отсекается этой параллельной прямой, эта окружность будет вневписанная. На построение какой окружности тогда намекает такое расположение?
Подсказка 6
Верно! На построение вневписанной окружности, которая касается BC. При этом, пусть AD пересекает BC в точке T1. У нас есть вписанная и вневписанная окружности. Что принято рассматривать, когда есть две окружности, вписанные в один угол и имеющие две параллельные соотвественные касательные?
Подсказка 7
Нужно рассмотреть гомотетию, с центром в точке А, переводящую вписанную окружность во вневписанную. Тогда, так как центр гомотетии, образ и точка лежат на 1 прямой, то выходит, что T1-точка касания вневписанной окружности стороны BC, так как AD пересекает BC именно в этой точке. Значит, A,D,T1 лежат на 1 прямой! А что это дает? Как связаны точки касания вписанной и вневписанной окружности?
Подсказка 8
Да, CT1=BK1(доказывается через обычный счет отрезков касания). Но при этом, М1-середина BC. То есть, от BC с концов отрезали равные отрезки (CT1 и BK1) и взяли середину. Значит, T1M1=M1K1. Так-так… А о чем задача? Ах да, нужно доказать, что AO и HK параллельны. Но при этом, на картинке у нас уже есть две параллельные прямые, которые отличны от тех, что в условии. Какие это прямые?
Подсказка 9
DK1=AH, по доказанному. При этом, они параллельны. Значит, AHK1D-параллелограмм. Значит, HK1 || AD. Но нам же нужно доказать, что HK1 || AO. Ого! Выходит, нам нужно доказать, что O лежит на прямой AD и задача решена? А равенство отрезков, доказанное ранее в пункте 8, может нам помочь?
Подсказка 10
Ну конечно, может! Только вот как бы это сделать?Хмм… А может быть, угадать эту точку на прямой AD? А вот если рассмотреть середину DT1…
Подсказка 11
Ничего себе! Если соединить середину DT1 с другой серединой - М1, то выходит, что этот отрезок будет перпендикулярен BC, при этом, будет равен половине DK1, то есть, равен IK1… Так это же отрезок M1O ! Значит O-середина DT1, а значит лежит на DT1, а значит и на AO !
Докажем сначала вспомогательное утверждение.
Пусть — середина стороны
,
(в условии это точка
) и
— точки касания вписанной и вневписанной окружностей
соответственно для треугольника
— диаметрально противоположна точке
во вписанной окружности.
Рассмотрим гомотетию с центром в точке переводящую вписанную окружность треугольника
во вневписанную окружность
этого треугольника, касающуюся стороны
Проведем прямую, проходящую через точку
и параллельную
В силу того, что
перпендикулярно и этой проведённой прямой. Но поскольку
— центр окружности, то наша прямая будет касательной,
а
— точкой касания. При этой гомотетии касательная к вписанной окружности, проведённая через точку
, переходит в прямую
(в силу их параллельности), значит, точка
переходит в точку касания
вневписанной окружности со стороной
Итог: точки
лежат на одной прямой.
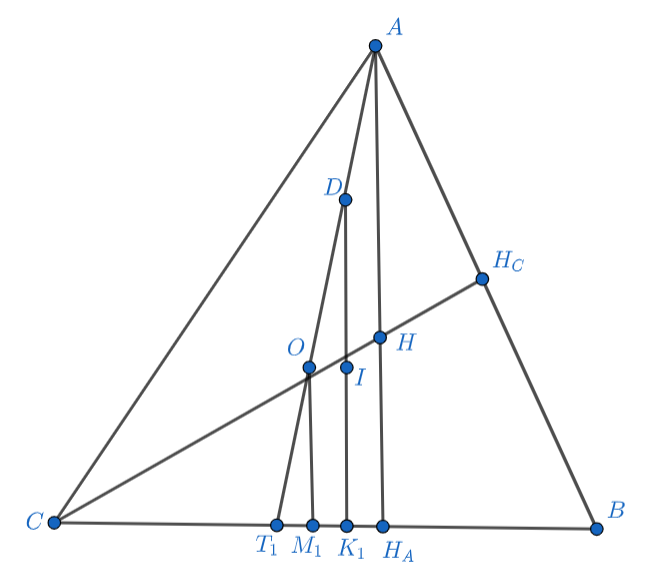
Решение.
Пусть пересекается с
в точке
Так как
из перпендикулярности
и хорошо известно, что
то
— средняя линия
и
При этом
откуда
— также средняя линия
и параллельна
откуда из условия задачи следует, что
В итоге имеем В силу перпендикулярности
мы знаем, что
Кроме того, по свойству ортоцентра
тогда
Так что
— параллелограмм, поэтому
Замечание.
Равенство можно проверить чисто технически: пусть
— высота
тогда
При этом
Ошибка.
Попробуйте повторить позже
Имеется несколько юношей, каждый из которых знаком с некоторыми девушками. Две свахи знают, кто с кем знаком. Одна сваха заявляет: “Я могу одновременно поженить всех брюнетов так, чтобы каждый из них женился на знакомой ему девушке!” Вторая сваха говорит: “А я могу устроить судьбу всех блондинок: каждая выйдет замуж за знакомого юношу!” Этот диалог услышал любитель математики, который сказал: “В таком случае можно сделать и то, и другое!” Прав ли он?
Источники:
Пусть каждый брюнет возьмёт правой рукой левую руку девушки, предназначенной ему первой свахой, а каждая блондинка возьмёт правой рукой левую руку юноши, предназначенного ей второй свахой. При этом образуются хороводы (циклы) и цепочки, которые содержат всех брюнетов, всех блондинок и, возможно, кого-то еще. Цепочки из чётного числа людей и хороводы (там чётное число людей ввиду чередования) разбиваются на пары знакомых, и их можно поженить.
Пусть цепочка состоит из нечётного числа людей и юношей в ней больше, чем девушек. Тогда на её концах стоят юноши и у одного из них свободна правая рука. Значит, он не брюнет, и его можно удалить из цепочки, а оставшихся переженить. Аналогично поступим с цепочкой, в которой больше девушек.
Прав
Ошибка.
Попробуйте повторить позже
Последовательность определяется так: первые её члены равны Далее каждый следующий (начиная с
-го) равен
произведению всех предыдущих членов минус
Докажите, что сумма квадратов первых
членов последовательности равна их
произведению.
Источники:
Подсказка 1!
В этой задаче нам потребуется один трюк. Чтобы доказать это, введем новую последовательность - такую, что ее n-ый член это разность a1a2a3...an и a1^2+a2^2...+an^2. И докажем, что 70ый член данной последовательности равен 0!
Подсказка 2!
Как бы это доказать? Вы знаете начальные члены последовательности, значит, надо как-то выразить n+1ый через nый, чтобы посчитать 70ый!
Пусть первоначальная последовательность была Введём новую последовательность
посчитаем
разность
для
Тогда Поскольку
то
что и требовалось.



