Ошибка.
Попробуйте повторить позже
Дан треугольник В нём
— точка пересечения высот,
— центр вписанной окружности,
— центр описанной окружности,
— точка касания вписанной окружности со стороной
Известно, что отрезки
и
параллельны. Докажите, что отрезки
и
также параллельны.
Источники:
Подсказка 1
Для начала, надо понять, что именно нам нужно доказывать, надо разбить нашу задачу на подзадачи, каждая из которых будет легче данной. Мы видим здесь ортоцентр и центр вписанной окружности. Из свойств ортоцентра, мы знаем, что расстояние от вершины до ортоцентра в два раза больше расстояния от центра описанной окружности до , противоположной этой вершине, стороны. Значит, стоит отметить середину BC и посмотреть, что это даст, учитывая условия задачи.
Подсказка 3
Высота из другой точки - точки I - это точка касания вписанной окружности. Значит, IK1=OM1(где К1-точка касания вписанной окружности со стороной BC). Но при этом, мы знаем, что OM1=AH/2, значит 2*IK1=AH. Где можно на картинке найти удвоенный отрезок IK1(радиус окружности)? Что это дает?
Подсказка 4
Удвоенный радиус вписанной окружности это, по сути, диаметр вписанной окружности. Значит, удобнее всего здесь отметить на этой окружности точку, диаметрально противоположную K1(искушенные читатели знают, что это совсем не простая точка).Пусть это точка D. Что тогда можно сказать про эту точку и точку А? В какой точке пересекает отрезок DA сторону BC? А если провести прямую, параллельную BC и проходящую через D?
Подсказка 5
Если провести такую прямую, то, во-первых, она будет касательной к вписанной окружности. Но при этом для треугольника, который отсекается этой параллельной прямой, эта окружность будет вневписанная. На построение какой окружности тогда намекает такое расположение?
Подсказка 6
Верно! На построение вневписанной окружности, которая касается BC. При этом, пусть AD пересекает BC в точке T1. У нас есть вписанная и вневписанная окружности. Что принято рассматривать, когда есть две окружности, вписанные в один угол и имеющие две параллельные соотвественные касательные?
Подсказка 7
Нужно рассмотреть гомотетию, с центром в точке А, переводящую вписанную окружность во вневписанную. Тогда, так как центр гомотетии, образ и точка лежат на 1 прямой, то выходит, что T1-точка касания вневписанной окружности стороны BC, так как AD пересекает BC именно в этой точке. Значит, A,D,T1 лежат на 1 прямой! А что это дает? Как связаны точки касания вписанной и вневписанной окружности?
Подсказка 8
Да, CT1=BK1(доказывается через обычный счет отрезков касания). Но при этом, М1-середина BC. То есть, от BC с концов отрезали равные отрезки (CT1 и BK1) и взяли середину. Значит, T1M1=M1K1. Так-так… А о чем задача? Ах да, нужно доказать, что AO и HK параллельны. Но при этом, на картинке у нас уже есть две параллельные прямые, которые отличны от тех, что в условии. Какие это прямые?
Подсказка 9
DK1=AH, по доказанному. При этом, они параллельны. Значит, AHK1D-параллелограмм. Значит, HK1 || AD. Но нам же нужно доказать, что HK1 || AO. Ого! Выходит, нам нужно доказать, что O лежит на прямой AD и задача решена? А равенство отрезков, доказанное ранее в пункте 8, может нам помочь?
Подсказка 10
Ну конечно, может! Только вот как бы это сделать?Хмм… А может быть, угадать эту точку на прямой AD? А вот если рассмотреть середину DT1…
Подсказка 11
Ничего себе! Если соединить середину DT1 с другой серединой - М1, то выходит, что этот отрезок будет перпендикулярен BC, при этом, будет равен половине DK1, то есть, равен IK1… Так это же отрезок M1O ! Значит O-середина DT1, а значит лежит на DT1, а значит и на AO !
Докажем сначала вспомогательное утверждение.
Пусть — середина стороны
,
(в условии это точка
) и
— точки касания вписанной и вневписанной окружностей
соответственно для треугольника
— диаметрально противоположна точке
во вписанной окружности.
Рассмотрим гомотетию с центром в точке переводящую вписанную окружность треугольника
во вневписанную окружность
этого треугольника, касающуюся стороны
Проведем прямую, проходящую через точку
и параллельную
В силу того, что
перпендикулярно и этой проведённой прямой. Но поскольку
— центр окружности, то наша прямая будет касательной,
а
— точкой касания. При этой гомотетии касательная к вписанной окружности, проведённая через точку
, переходит в прямую
(в силу их параллельности), значит, точка
переходит в точку касания
вневписанной окружности со стороной
Итог: точки
лежат на одной прямой.
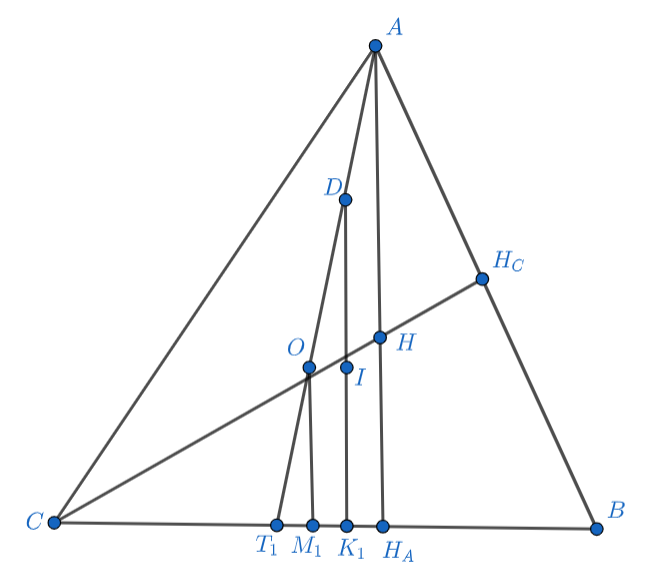
Решение.
Пусть пересекается с
в точке
Так как
из перпендикулярности
и хорошо известно, что
то
— средняя линия
и
При этом
откуда
— также средняя линия
и параллельна
откуда из условия задачи следует, что
В итоге имеем В силу перпендикулярности
мы знаем, что
Кроме того, по свойству ортоцентра
тогда
Так что
— параллелограмм, поэтому
Замечание.
Равенство можно проверить чисто технически: пусть
— высота
тогда
При этом
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное обучение
в Школково
Для детей ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Брянской областей, а также школьникам, находящимся в пунктах временного размещения Крыма обучение на платформе бесплатное.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ или олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




