Ошибка.
Попробуйте повторить позже
Дан отрезок Точки
в пространстве выбираются так, чтобы
был правильным треугольником, а
– квадратом.
Докажите, что ортоцентры всех получающихся таким образом треугольников
попадают на некоторую фиксированную
окружность.
Источники:
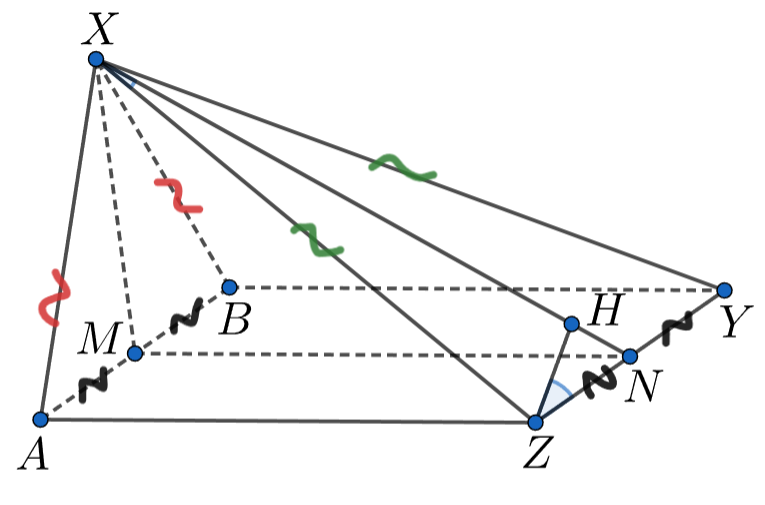
Пусть — середина
— середина
Рассмотрим плоскость
Заметим, что прямая
перпендикулярна прямым
и
а значит она перпендикулярна плоскости
Следовательно,
Нетрудно видеть, что при симметрии
относительно плоскости
отрезок
перейдёт в отрезок
то есть
Таким образом, ортоцентр
треугольника
лежит на отрезке
— серединном перпендикуляре
Покажем, что лежит на окружности
с центром
радиусом
лежащей в плоскости
Для этого определим на
отрезке
точку
такую, что
и точку
— вторичное пересечение прямой
с
Осталось посчитать, что
четырёхугольник
— вписанный, то есть доказать равенство
Пусть длина стороны квадрата и правильного треугольника равна Из подобия треугольников
и
нетрудно получить,
что
Также понятно, что
откуда
Получили
нужное равенство.
Ошибка.
Попробуйте повторить позже
Дан отрезок . За ход разрешается разбить любой из имеющихся отрезков точкой на два новых отрезка и записать на
доску произведение длин этих двух новых отрезков. Докажите, что ни в какой момент сумма чисел на доске не превысит
.
Источники:
Подсказка 1
Давайте попытаемся понять, как выглядит сумма чисел на доске в общем виде. Начнём разбивать наш отрезок и записывать числа. На втором разбиении попробуйте заменить один из отрезков на сумму двух. У вас получится просто сумма попарных произведений всех длин. Как тогда наша сумма будет выглядеть в общем виде? Докажите это по индукции.
Подсказка 2
Верно, в итоге, у нас получится сумма всевозможных попарных произведений отрезков. База понятна, а дальше нужно по аналогии в сумме заменить длину вновь разбитого отрезка через сумму двух новых. Отлично, с этим справились! Заметим, что нам известна сумма всех отрезков. Как можно выразить теперь сумму попарных произведений для удобной оценки?
Подсказка 3
Точно, ведь нашу сумму можно выразить через разность квадрата суммы всех отрезков и суммы квадратов каждого из отрезков. Только нужно ещё поделить пополам. Вот тут нам и пригодится знание про сумму отрезков. Осталось понять, почему мы получили требуемое, и победа!
Пусть через шагов мы поделили отрезок на отрезки
. Индукцией по
покажем, что сумма чисел, записанных на доске,
равна сумме всевозможных попарных произведений чисел
.
База очевидна.
Переход: Пусть на шаге сумма равна
. На
-м шаге мы делим
-й отрезок на отрезки
и
, тогда
сумма примет вид:
В данном случае — попарные произведения чисел
без
, а
— сумма этих же
чисел без
. Таким образом, на
-м шаге также получили всевозможные попарные произведения.
Тогда задача свелась к тому, что нужно доказать, что сумма всевозможных попарных произведений чисел меньше , если их сумма
равна
, а это следует, например, из того, что:
Ошибка.
Попробуйте повторить позже
В ящике лежат шариков: красные, синие, зелёные и белые. Известно, что если, не заглядывая в ящик, вытащить
шариков, то
среди них обязательно найдутся четыре шарика различных цветов. Какое наименьшее число шариков нужно вытащить, не заглядывая в
ящик, чтобы среди них наверняка нашлись три шарика различных цветов?
Источники:
Подсказка 1!
1) Давайте попробуем посмотреть на условие про 100 шариков под другим углом.. Например, о чем оно может сказать в контексте количества шариков одного цвета?
Подсказка 2!
2) Верно, каждого не меньше 12! Ведь иначе найдется 100 шариков без него
Подсказка 3!
3) Теперь нам бы посмотреть под другим углом и на то, что нам нужно получить! То есть сколько щариков точно можно вытянуть, чтобы условие не выполнялось? А сколько еще надо, чтобы оно выполнилось?
Если шариков какого-то цвета меньше , то найдётся набор из
шариков, в котором этого цвета нет. Значит, шариков каждого цвета
не менее
. Отсюда шариков любых двух цветов не больше
, то есть достаточно вытащить
шариков и среди них
гарантированно будет
шарика разных цветов.
Почему нельзя вытащить меньше , чтобы наверняка нашлись шарики трёх разных цветов? Рассмотрим такой набор
по цветам:
красных и по
синих, зелёных и белых. Если вытаскивать меньше
шариков, то можно вытянуть
только красные или синие шарики, которых в сумме как раз меньше
. Будет набор шариков только из двух цветов, не из
трёх.
Ошибка.
Попробуйте повторить позже
В бесконечной последовательности натуральных чисел каждое следующее число получается прибавлением к предыдущему одной из его ненулевых цифр. Докажите, что в этой последовательности найдётся чётное число.
Источники:
Подсказка 1
Давайте подумаем, что означает, что все числа в последовательности нечетные? Это значит, что для любого числа из последовательности выполнено, что мы можем взять в нем четную цифру(чтобы не менять четность соседних чисел в последовательности). Значит, если мы хотим прийти к противоречию, то надо доказать, что найдется число, в котором нет четных цифр.
Подсказка 2
А это значит, что надо доказать, что найдется число, что все его цифры будут нечетные! Хмм… А что означает, что на некотором месте, стоят всегда четные цифры(если идти от противного)?
Подсказка 3
Это значит, что существует момент, когда при добавление числа, не больше 9(так как это цифра), мы перепрыгиваем сразу на 2, в каком-то разряде, который не является разрядом единиц(так как если бы там стояло что-то четное, то мы уже победили). А возможно ли это?
Подсказка 4
Нет, это невозможно, так как если мы перепрыгиваем сразу на 2 разряда, то это хотя бы разряд десятков, значит разница между начальным и конечным числом(после прибавления цифры) больше 10. Однако, мы прибавляем что-то меньшее 1. Пришли к противоречию.
Поймём, что числа в нашей последовательности точно больше то есть, имеют длину хотя бы
так как если бы в нашей
последовательности было бы число длины
то следующее за ним определялось бы как сумма этого числа, как цифры себя и его самого.
То есть, мы бы просто удвоили наше число и получили бы четное число. Значит, длина всех наших чисел из последовательности хотя бы
Тогда возьмём первое число из нашей последовательности. Пусть в нем разрядов. Рассмотрим первую цифру слева. Если эта
цифра нечетная, то дальше рассмотрим
-ую слева цифру. Иначе, понятно, что рано или поздно, прибавляя по числу
меньшему
-ая цифра станет нечетной, так как чтобы она перепрыгнула через нечетное число за одно прибавление, мы
должны прибавить как минимум
но мы прибавляем не больше
Значит, рано или поздно первая слева цифра станет
нечетной.
Посмотрим теперь на вторую слева цифру и повторим наши рассуждения. Тогда, при условии того, что первая цифра все еще нечетна,
рано или поздно вторая станет также нечетной. Аналогично, найдется момент, когда и первая, и вторая, и третья цифры нечетны и тд.
Значит, найдется момент, когда цифры нечетны. При этом последняя цифра всегда нечетна, так как если она в какой-то
момент стала четной, то мы победили, найдя четное число. Значит, найдется такое число в последовательности, что все его цифры
нечетные.
Значит, какую бы цифру мы не прибавили, мы прибавим что-то нечетное, а сумма двух нечетных(нашего числа и выбранной цифры) четна. Итак, мы получим четное число в последовательности.
Ошибка.
Попробуйте повторить позже
Через вершину остроугольного треугольника
проведены касательная
к его описанной окружности, а также биссектрисы
и
внутреннего и внешнего углов при вершине
(точки
и
лежат на прямой
). Докажите, что
Источники:
Подсказка 1
Давайте подумаем, что легче доказывать: равенство отрезков или равенство углов? Понятно, что в разных задачах по-разному, но тут через углы проще. Как тогда можно заменить условие задачи на равносильное утверждение? То есть, принять верным вопрос задачи, но тогда доказать какой-то факт из условия. Это очень частая практика в задачах по планиметрии.
Подсказка 2
Верно, предположим мы знаем, что K — это середина отрезка. Тогда докажем, что AK — это касательная. Это будет равносильная задача. Теперь тогда равенство каких углов нам нужно доказать?
Подсказка 3
Да, теперь нам нужно, чтобы ∠KAB = ∠ACB. Тогда давайте введём неизвестный ∠KAB=α и посчитаем уголочки. Осталось только воспользоваться другими фактами задачи: мы знаем, что AK — медиана в прямоугольном треугольнике и AN биссектриса. Попробуйте применить всё это, и победа!
Заметим, что середина отрезка является центром окружности Аполлония точек
и
с коэффициентом
Поэтому можно
предположить, что
— центр окружности Аполлония и доказать, что
— касательная к описанной окружности. Это равносильно
изначальной задаче, потому что касательная пересекает
в одной точке.
Итак, поскольку биссектрисы смежных углов перпендикулярны. Нам нужно доказать равенство углов
и
тогда по обратной теореме об угле между хордой и касательной мы получим требуемое.
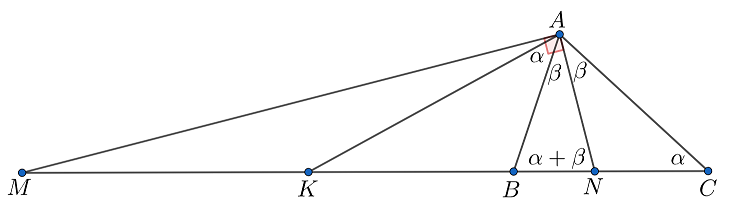
Обозначим угол через
, а углы
и
— через
. Отрезок
— медиана, проведённая к гипотенузе, а значит
, то есть
. Осталось заметить, что угол
— внешний у треугольника
. Таким образом,
. Получили требуемое.



