Заметим, что

Здесь мы оценили знаменатель по неравенству о средних:

Сложим полученное неравенство с тремя аналогичными. Теперь нам достаточно доказать, что

Поскольку это равносильно неравенству

Но из неравенства между средним арифметическим и среднем квадратичным мы получаем, что

и, аналогично,

Складывая эти два неравенства, получаем требуемое.

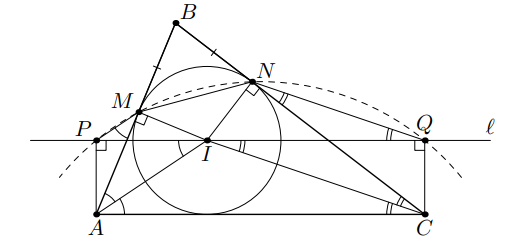
Пусть углы и треугольника равны, соответственно и Углы и — прямые, поэтому точки лежат на одной окружности с диаметром Тогда (в силу параллельности) Аналогично Из равнобедренного треугольника находим: Тогда Но значит, сумма углов и равна то есть точки и лежат на одной окружности.

Первое решение. Обозначим то есть степени рассматриваемых многочленов равны

Лемма. Существует единственный многочлен степени (со старшим коэффициентам ) такой, что степень полученного многочлена будет меньше, чем

Доказательство. Запишем наш многочлен как

Обозначим и это — многочлены степени со старшим коэффициентом

В многочлене коэффициент участвует лишь в членах степени, не большей Значит, для любого коэффициент при в многочлене зависит лишь от коэффициентов при С другой стороны, коэффициент при этой же степени в есть где зависит лишь от коэффициентов при Если мы хотим, чтобы степень была меньше, чем то эти коэффициенты должны быть равны; это равенство даёт однозначное выражение через (в частности, находится единственным образом). Значит, из этих равенств по очереди находятся все коэффициенты многочлена

Теперь достаточно предъявить многочлен такой, что степень окажется меньше, чем — по лемме, он единственный, и он и даст минимальную степень Положим Тогда многочлен

имеет степень всего лишь Значит, наименьшая возможная степень и есть

Второе решение. Используем те же обозначение и что и в первом решении. Мы будем считать, что

(впоследствии мы увидим, что это возможно; поэтому для многочлена минимальной степени так считать можно).

Предположим, что в многочлене есть одночлен степени, не кратной пусть — такой одночлен наибольшей степени. Тогда коэффициент многочлена при равен что противоречит неравенству.

Таким образом, в предположении, степени всех одночленов в кратны иначе говоря, существует такой многочлен что Тогда

то есть где

при этом а предположение означает, что

Рассмотрим многочлен тогда Аналогично рассуждению выше, предположим, что то есть в многочлене есть одночлены, кроме пусть — такой одночлен наибольшей степени. Тогда в многочлене есть одночлен что противоречит неравенству Таким образом, а тогда и Мы приходим к тому же примеру, что и в первом решении (и видим, что в этом случае степень действительно удовлетворяет (*)).

Заметим сразу, что все числа, появляющиеся на доске, положительны и рациональны. Пусть — числа на доске после минут, а — исходные числа.

Положим Тогда и В частности, и, аналогично,

Положим и пусть — представление этого числа в виде несократимой дроби. Тогда и потому

где последняя дробь также несократима (ибо и взаимно просты). Итак, и В частности, при и потому при Иными словами, последовательность строго возрастает.

Обозначим через произведение всех числителей и знаменателей чисел и Тогда при некотором имеем

Докажем, что с -й минуты все числа на доске нецелые. Действительно, пусть, скажем, — целое при Тогда и потому

Знаменатель этого числа в несократимой записи делит но это невозможно, ибо Противоречие.

Пусть и Тогда и Возведём эти равенства в квадрат и сложим их. Тогда в силу основного тригонометрического тождества получим: то есть Пусть — НОК знаменателей чисел и тогда, умножив полученное равенство на получим требуемое.

Например, подходит

Разобьём доску на квадратов прямоугольников и один квадрат (см. рис. слева). В каждом квадрате клетки разбиваются на четвёрок так, что расстояние между любыми клетками в одной четвёрке равно (каждая четвёрка состоит из клеток с координатами ). Тогда в любой четвёрке может быть отмечено не более одной клетки, то есть общее число отмеченных клеток в таком квадрате не превосходит

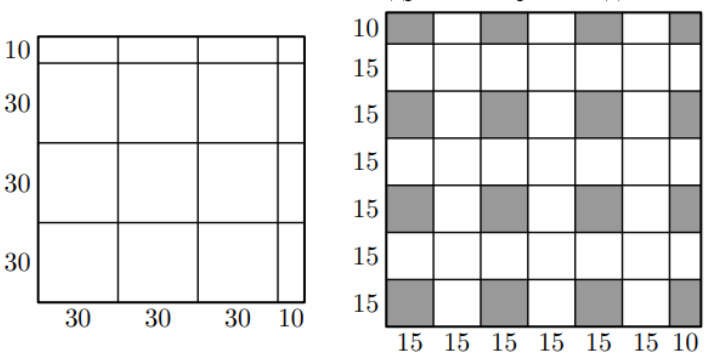
Аналогично, каждый прямоугольник (скажем, с длинной горизонтальной стороной) разбивается на пары клеток, отстоящих друг от друга на (с координатами и ) — поэтому в нём не более отмеченных клеток. Наконец, в квадрате всего клеток. Итого, отмеченных клеток не больше, чем

Пример с таким количеством отмеченных клеток показан на рис. справа.

Для каждого натурального обозначим Каждому ученику сопоставим множество всех дней, когда он ходил в бассейн (это будет подмножество в ). Итого, мы получили набор из (согласно условию, непустых) подмножеств в Условие равносильно тому, что во всех подмножествах разные количества элементов, и ни одно из них не содержится в другом; назовём такой набор подмножеств хорошим. Таким образом, нам нужно найти максимальное число множеств в хорошем семействе подмножеств в

Докажем сначала, что такой набор не может содержать больше множеств. Это очевидно, если в наборе есть -элементное подмножество, так как оно содержит любое другое. Значит, можно считать, что множества в наборе могут состоять лишь из элементов (и их не больше ). Пусть в хорошем наборе есть -элементное множество и -элементное множество Так как не содержится в они не пересекаются. Тогда любое другое подмножество в либо содержит либо содержится в Значит, в этом случае хороший набор состоит лишь из двух подмножеств. Наконец, если в наборе нет или -элементного подмножества, то в нём уже не более множеств, что и требовалось.

Осталось предъявить пример хорошего набора из подмножеств в Для этого покажем индукцией по что существует хороший набор подмножеств в причём содержит элемент. В базовом случае годятся подмножества и

Пусть для некоторого уже построен требуемый хороший набор подмножеств в Тогда требуемый хороший набор подмножеств в можно построить так. Положим при эти множества содержат элементов соответственно. Наконец, положим и Нетрудно проверить, что они образуют требуемый хороший набор. Тем самым переход индукции доказан.

Понятно, что и целые, так как выражаются через целые корни по теореме Виета. Для того, чтобы квадратный трёхчлен с целыми коэффициентами имел целые корни, необходимо, чтобы его дискриминант был точным квадратом. Таким образом, откуда то есть Последнее равенство равносильно двум случаям и и Первый случай целых решений не даёт, а второй — Таким образом, Заметим, что дискриминант трёхчлена равен а значит он действительно не имеет корней, что и требовалось.

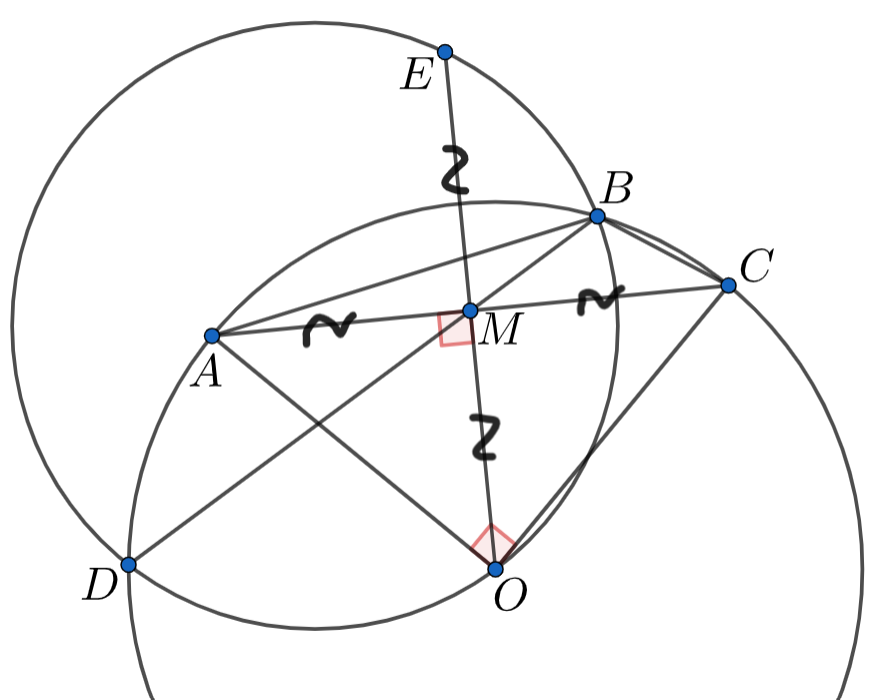
Так как то Так как — медиана в прямоугольном треугольнике имеем На продолжении отрезка за точку отметим точку так, что Поскольку четырёхугольник вписанный, Следовательно, точка лежит на окружности Точка лежит на серединном перпендикуляре к отрезку поэтому Значит, прямая является серединным перпендикуляром к отрезку Поскольку отрезок является хордой окружности её центр лежит на прямой

Подставим в данное равенство вместо Получим

Итак, откуда для всех действительных получим Это и означает, что функция чётная.

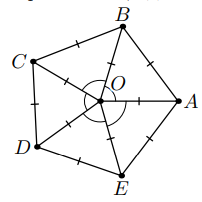
Сначала докажем, что все отрезков не могут иметь длину Предположим противное. Пусть — пятиугольник, — точка внутри него, и все проведенных отрезков имеют длину (см. рис. выше). Тогда треугольники и — правильные, поэтому Сумма же этих углов должна быть равна однако — противоречие.

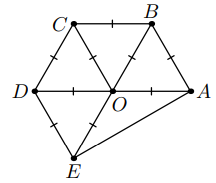
Осталось привести пример, когда отрезков имеют длину (см. рис. выше). Отметим на плоскости точки и на расстоянии выберем последовательно точки и так, чтобы треугольники и были равносторонними. Тогда точка лежит внутри пятиугольника и из проведенных отрезков все, кроме имеют длину

Покажем, что требуемому условию удовлетворяют любые два столбца таблицы. Выкинем из таблицы все столбцы, кроме двух рассматриваемых. Общее число нулей в этих столбцах больше общего числа единиц; это значит, что нулей в них не меньше Если в полученной таблице строк с двумя нулями, то есть ещё хотя бы строк с одним нулём — и, следовательно, не более столбцов с двумя единицами. Осталось заметить, что

Пусть в зоопарк было пар особей и детёнышей. Тогда каждый детёныш состоял в тройках: самку можно было выбрать из одной из пар особей, а после её выбора самца можно было выбрать из одной оставшихся пар. Значит, общее количество троек равно

Поскольку получаем то есть Значит,

Число имеет два делителя и отличающиеся на Если один из этих делителей делится на то другой даёт остаток или при делении на Тогда он взаимно прост с а значит, делит и при этом не меньше Нетрудно видеть, что этим делителем может быть только тогда

Если же оба числа не делится на , то число делится на их произведение, а это противоречит тому, что

Пример. Произведение знаменателей может быть равным Один из возможных примеров:

Оценка. Пусть значение исходного выражения равно Тогда в результате первой операции произведение примет значение

откуда Значит,  – натуральное число, кратное 3. Аналогично доказывается, что Ясно, что делится на поэтому

Переписав равенство в виде получаем откуда

Покажем, что ладей достаточно. Для этого заметим, что на каждую строку хватит одной ладьи: можно поставить её в клетку строки с минимальным номером, а затем обойти все клетки строки в порядке возрастания номеров.

С другой стороны, покажем, что меньше, чем ладей, может и не хватить. Для этого пронумеруем клетки так, чтобы клетки одной диагонали были пронумерованы (остальные клетки нумеруем произвольно). Тогда одна ладья не сможет побывать на двух клетках этой диагонали: если ладья встала на одну из этих клеток, то следующим ходом она обязана будет пойти на клетку с номером, большим и значит, после этого она не сможет вернуться на диагональ.

Наконец, поскольку на каждой клетке диагонали должна побывать ладья, Пете придётся использовать не менее ладей.

Числа и делятся на Значит, числа и также делятся на так что делится на

С другой стороны, Первое слагаемое делится на а второе — нет. Итак, является делителем числа и не делится на значит, — делитель числа

Расположим систему отсчета так, чтобы начало отсчета совпало с центром прямоугольника, а вершины прямоугольника попали на единичную окружность. Тогда Точка лежит на хорде откуда Тогда Обозначим через точку пересечения медиан треугольника Тогда комплексную координату можно вычислить Заметим, что Тогда

Вспомнив, что получаем, что последнее выражение вещественное.

Предположим, что да. Подставим в оба трёхчлена, приравняем полученные значения и после тождественных преобразований получим

При первый трёхчлен равен

Но на не делится. Пришли к противоречию.

Назовём беспосадочный перелёт из одного города в другой коротким маршрутом, а перелёт из одного города в другой с одной пересадкой в пути длинным маршрутом. Перенумеруем города и обозначим через число рейсов, выходящих из -го города.

Будем учитывать короткие маршруты в их конечных пунктах, а длинные — в пунктах пересадки. Тогда, если из города выходит авиалиний, то в нём будет учтено коротких маршрутов и длинных (так как из каждого смежного города через данный проходит длинных маршрутов), а всего — маршрутов. Таким образом, общее число маршрутов равно

Поскольку в любой степени при делении на дает остаток то остаток от деления на у общего числа маршрутов такой же, как у числа то есть а у числа этот остаток равен