Ошибка.
Попробуйте повторить позже
В классе мальчиков и
девочек (
Они расселись за круглым столом так, что никакие два мальчика и никакие две девочки не
сидят рядом. У учителя есть
карточек, на них написаны числа
каждое по одному разу. Он так раздал каждому
школьнику по одной карточке, что число у любой девочки больше числа у любого мальчика. Затем каждая девочка написала на листочке
сумму чисел на трех карточках: ее собственной и сидящих рядом с ней мальчиков. При каких
все полученные
чисел могли оказаться
равными?
Источники:
Подсказка 1
По условию понятно, что у мальчиков карточки от 1 до n, а у девочек - от n+1 до 2n. Вот пусть у девочек все суммы вышли равными какому-то m. Тогда можно ли понять, чему равно m?
Подсказка 2
Например, сумма всех чисел, полученных у девочек, будет равна mn. А с другой стороны, это сумма чисел девочек + удвоенная сумма чисел мальчиков) Посчитайте, чему тогда будет равно m.
Подсказка 3
Выйдет, что m = 2n+1 + (n+1)/2, откуда уже понятно, что n - нечетное. Можно ли для любого нечетного n подобрать пример?
Подсказка 4
Можно) Но нужно понять как. Может быть, можно как-то раздать мальчикам карты хорошо, а после по карточкам мальчиков понять, какие у каждой девочки должны быть карты?
По условию мальчики получили карточки с числами от 1 до а девочки карточки с числами от
до
Предположим, что у всех
девочек на листочках оказалось написано число
Тогда сумма всех чисел на листочках равна
с другой стороны она может быть
получена следующим образом: надо сложить все числа, которые есть у девочек и добавить к ним удвоенную сумму всех чисел, которые есть
у мальчиков.
Следовательно,
Стало быть, и
— нечетно. Пусть
тогда
Для примера надо последовательно раздать
карточки мальчикам от 1 до
идя через одного. Если теперь для каждой девочки посмотреть на сумму чисел, на карточках соседних
с ней мальчиков, то по одному разу получатся все суммы от
до
Дальше нужно дополнить их числами от
до
(раздав соответствующие карточки девочкам) так, чтобы все суммы стали равны
Пример раздачи карточек для
и
показан на рисунке.
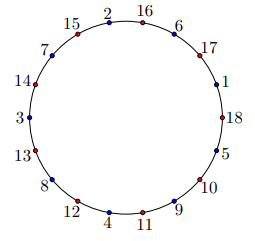
при нечетных
Ошибка.
Попробуйте повторить позже
В каждой клетке таблицы записано натуральное число. В каждой строке имеется по крайней мере 10 различных чисел, а в
каждых четырех последовательных строках не более 15 различных чисел. Какое наибольшее количество различных чисел может быть в
таблице?
Источники:
Подсказка 1
У нас в каждой строке не менее 10 различных чисел, в подряд идущих четырех строчках не больше 15 различных...как будто следующие 3 строчки дают не очень много новых различных чисел. Это наблюдение легко сделать строгим, и останется привести пример)
Подсказка 2
Если вышло, что различных чисел не больше 175, это хорошо. Тогда вот идея для примера: в первой строчке давайте сделаем все числа от 1 до 10, а в 2, 3 и 4 поставим числа от 1 до 5 и от 11 до 15. Придумайте, как это обобщить на всю нашу доску)
В одной строке не менее 10 различных чисел, поэтому в следующих трех строках вместе появляется не более 5 новых чисел. Стало быть,
первые четыре строки содержат не более 15 различных чисел, а каждые следующие три строки дают не более 5 новых чисел и всего чисел не
больше, чем
Приведем пример на 175 чисел. Занумеруем строки числами от 1 до 100. В первой строке поставим числа от 1 до 10, а в строке с
номерами от до
поставим числа 1 до 5 и числа от
до
Тогда в каждой строке будет 5 уникальных чисел и
еще числа от 1 до 5, т.е. ровно 10 различных чисел, а в каждых четырех строках будет ровно 15 различных чисел. Таким образом, в таблице
будут числа от
до
Замечание.
Доказать, что количество различных чисел в таблице не превосходит 175, можно по индукции. А именно, доказать, что в любых
подряд идущих строках расположено не более чем
различных чисел. База
верна по условию. Установим
переход от
к
Рассмотрим
подряд идущие строки. Пусть в четвертой с конца строке имеется
различных чисел. Тогда в трех самых нижних строках не более чем
различных чисел. А в оставшихся
строке по индукционному предположению не больше
чисел. Поэтому всего различных чисел будет более чем
Ошибка.
Попробуйте повторить позже
При каких клетчатую доску
можно разбить по клеточкам на один квадрат
и некоторое количество полосок из пяти клеток
так, что квадрат будет примыкать к стороне доски?
Источники:
Подсказка 1
Если так вышло, что мы смогли разрезать на квадрат 2*2 и полоски из 5 клеток, то что можно сказать про n? А если рассмотреть его по модулю 5? Тут неопытный читатель может спросить, почему именно 5? Это связано с тем, что мы как бы от нашего квадрата отрезаем полоски длины 5, значит, вычитаем каждый раз 5, и еще 5, и т.д. Значит, остаток mod 5 инвариантен. Поэтому именно по этому модулю надо рассматривать n.
Подсказка 2
Верно, что n² = 2² (mod 5), так как кол - во клеток с одной стороны это n² , с другой стороны - это сумма клеток квадрата и полосок по 5. Значит, либо n = 5k - 3, либо n = 5k + 3. Если верно последнее, то нужно еще проверить, что квадрат 2*2 примыкает к границе. Теперь, попробуйте как-то зафиксировать квадрат, то есть быть может как-то раскрасить и/или заполнить числами таблицу, чтобы числа в квадрате(цвета) были фиксированы. Иными словами, почему мы хотим так делать? Потому что у нас нет явного параметра, который сказал бы, что квадрат примыкает к таблице и мы хотим такой сделать. Что - то типа аналога координат.
Подсказка 3
Действительно, заполним первую строку единицами, вторую - двойками и т.д. Теперь нам надо посчитать по модулю 5 с двух сторон сумму чисел в таблице. Попробуйте это сделать и прийти к противоречию.
Подсказка 4
С одной стороны, так как сумма 5 подряд идущих строк кратна 5(просто потому что у нас в каждом столбце будут все остатки mod 5, а значит их сумма будет кратна 5, и таких столбцов n), а значит останутся только 3 первые строки, а сумма чисел в остальной таблице будет кратна 5. Значит, с одной стороны сумма чисел в таблице по модулю 5 - это n + 2n + 3n = n = 3 (mod 5). C другой стороны, если мы разрезаем на полоски длины 5 и квадрат, сумма в котором 1 + 1 + 2 + 2(так как он находится в первых двух строках. Ровно для этого мы и расставляли числа, чтобы зафиксировать наш квадрат где нужно) и равна 1 по модулю 5. Значит, пришли к противоречию, так как одинаковая величина имеет разный остаток при делении на 5. Значит, случай с n = 3 (mod 5) неразрешим. Остался n = 2 (mod 5). Тут уже вряд ли тоже ответ «нет», так как тогда вообще таких квадратов не бывает, но кажется такой квадрат можно подобрать, как минимум n = 2. Попробуйте для общего вида n = 2 (mod 5) привести пример.
Подсказка 5
Да, мы можем просто поставить квадрат 2*2 в левый верхний угол. Тогда, у нас оставшиеся две части первых двух строк и первых двух столбцов, по длине будут делиться на 5, а значит мы их можем разделить на полоски по 5. А с оставшейся частью таблицы что делать?
Если доску удалось разрезать на один квадрат
и некоторое количество полосок из пяти клеток, то
, откуда
дает остаток 2 или 3 от деления на 5. Предположим, что
и доску удалось разрезать требуемым образом.
Развернем ее так, чтобы квадрат примыкал к верхней стороне доски. Запишем в клетках верхней строки единицы, в клетках
следующей за ней строки — двойки, и так далее. Заметим, что сумма чисел в пяти последовательных строках кратна 5,
поскольку
Поэтому остаток от деления на 5 суммы всех расставленных чисел равен
С другой стороны, в каждой полоске сумма чисел кратна пяти, а в квадрате сумма чисел равна Значит, остаток от
деления на 5 суммы всех расставленных чисел равен 1 , и мы получаем противоречие.
Если то можно вырезать угловой квадрат
верхнюю полоску
разрезать на горизонтальные полоски из пяти
клеток, а прямоугольник
разрезать на вертикальные полоски из пяти клеток.
при
Ошибка.
Попробуйте повторить позже
В некоторых клетках полоски поставлено по одной фишке. В каждую из пустых клеток записывается число, равное модулю
разности количества фишек слева и справа от этой клетки. Известно, что все записанные числа различны и отличны от нуля. Какое
наименьшее количество фишек может быть расставлено в клетках?
Источники:
Подсказка 1!
Итак, попробуем проанализировать, как вообще выглядят эти числа в пустых клетках. Давайте подумаем, насколько они могут быть большие, и какая у них может быть четность!
Подсказка 2!
Да, так как при переходе через фишку модуль разности изменяется на четное число, разности всегда одной четности, и, конечно, не могут быть больше n (за n возьмем число фишек)! Так-так-так, ну, теперь давайте поймем, а сколько их вообще тогда может быть?
Подсказка 3!
Верно, их не больше половины n. А всего их 2021-n... Попробуйте доделать оценку и пример!
Пусть количество расставленных фишек равно Заметим, что числа в пустых клетках лежат в диапазоне от
до
и имеют
одинаковую четность, поскольку при переходе через блок из фишек размера
значение числа поменяется на
чётность модуля не
поменяется. По принципу Дирихле количество пустых клеток (равное
) не больше половины, то есть не больше
То
есть
Осталось привести пример для
где единицами обозначены фишки, а нулями — пустые клетки. Здесь в пустых ячейках окажутся числа
Ошибка.
Попробуйте повторить позже
Какое наибольшее количество ладей можно расставить на шахматной доске так, чтобы каждую ладью било не более трех других? Ладья не бьет насквозь через другую фигуру.
Пусть — число некраевых ладей (не стоящих с краю). Каждая такая ладья бьёт хотя бы одну свободную краевую клетку
(иначе она била бы четыре ладьи, закрывающие эти клетки). Значит, на периметре доски имеется по крайней мере
пустых клеток, а на некоторых из остальных
клеток периметра могут стоять ладьи. Таким образом, всего на доске
может быть не более
ладей. Пример для
ладей можно получить, если расставить ладей по периметру
доски.
Ошибка.
Попробуйте повторить позже
Имеется черных ладей и
белых. При каком наибольшем
их можно расставить на шахматной доске так, чтобы одноцветные ладьи
не били друг друга? Ладья не бьет насквозь через другую фигуру.
Пусть в -й строке доски стоит
чёрных ладей. Тогда в этой строке можно расположить не более
белых ладей, не бьющих друг
друга. Поэтому
Расстановка для белых ладей показана на рисунке:

Ошибка.
Попробуйте повторить позже
Имеется один черный ферзь и белых. При каком наибольшем
эти фигуры можно расставить на шахматной доске так, чтобы белые
ферзи не били друг друга? Ферзь не бьет насквозь через другую фигуру.
Источники:
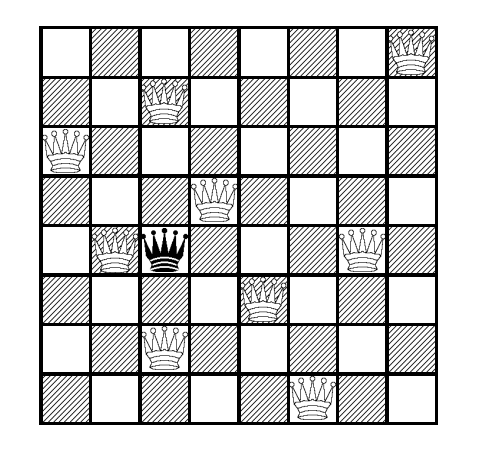
В строке, где стоит чёрный ферзь, может быть не более двух белых ферзей , не бьющих друг друга. В остальных строках не может быть
более одного ферзя. Таким образом, общее число белых ферзей не превосходит
Пример для показан на рисунке.
Ошибка.
Попробуйте повторить позже
Какое наибольшее количество фишек можно расставить на клетчатой доске так, чтобы на каждой диагонали располагалось не
более пяти фишек?
Пусть — диагональ, соединяющая левый нижний угол с правым верхним, а
— диагональ, соединяющая правый нижний угол с
левым верхним. Упорядочим диагонали, параллельные
сверху вниз. Пять первых и пять последних диагоналей содержат в общей
сложности
клеток, из которых
лежат на
Значит, на этих десяти диагоналях может располагаться не более
фишек. Остальные
диагоналей содержат не более чем по
фишек. Поэтому общее число фишек не превосходит
Пример на фишки:

Ошибка.
Попробуйте повторить позже
При каком наибольшем на шахматной доске можно расставить
королей и
ладей так, чтобы никакая фигура не была под
боем?
Источники:
Подсказка 1!
Давайте посмотрим, если мы будем расставлять только ладей. Всего сколько небьющих ладей можно поставить на доске?
Подсказка 2!
Верно, всего 8, так как у нас всего 8 столбиков, а они все стоят в различных столбиках. Давайте попробуем теперь доказать, что n не 7. Сколько в таком случае можно поставить на доску королей?
Подсказка 3!
Осталось понять что-то со случаем, когда n это 6. И не забыть построить пример на верную оценку)
Если то ладьи стоят в различных строках и столбцах, потому для королей, чтобы их не били остаётся не более
строк и не более
столбцов. То есть на хотя бы
королей не более
клеток, что невозможно. Значит,
Для сначала расставим короли в клетках
то есть как можно ближе к углу
но так, чтоб друг друга они
не били и занимали не более трёх строк и столбцов. Осталось расставить ладьи. Например, можно выбрать для них клетки
Ошибка.
Попробуйте повторить позже
В таблице расставлены
чисел так, что все шесть произведений этих чисел в строках и в столбцах таблицы различны. Какое
наибольшее количество чисел в этой таблице может равняться единице?
Источники:
Подсказка 1!
Решаем методом "сначала попробовать, потом подумать". Попытацтесь сначала расставить максимально, сколько сможете. Давайте посмотрим, если все элементы это 1, то ничего хорошего не будет, все произведения одинаковы. Тогда в каком-то столбике есть хоть одно неединичное.
Подсказка 2!
Да, но с ним вместе либо в столбике, либо в строке, тоже должно быть неединичное, иначе в этой строчке и столбце мы получим одинаковые значения.
Подсказка 3!
То есть мы поняли, что неединичные числа встречаются парами. Тогда попробуем оценить, сколько должно быть пар, и, следовательно, чисел!
Подсказка 4!
дааа, пар всего пять. Тогда сколько вообще может быть неединичных чисел-то в итоге? Попробуйте использовать количество пар и строк, и столбцов, которые они занимают.
Очевидно, что в таблице есть неединичное число. В одной строке или в одном столбце с ним есть ещё одно неединичное, потому что иначе произведения по строке и столбцу будут равны этому числу, что противоречит их различности.
Значит, неединичные элементы встречаются парами. Одна пара влияет на три произведения — строку и два столбца или наоборот.
Неединичных произведений хотя бы поэтому пары хотя бы две. Если пар хотя бы три, то неединичных чисел хотя бы
(если элементов
то все они лежат в одной строке, тогда произведения в других строках единичные и равны, аналогично со столбцами). Если же пары
ровно две, то в случае их пересечения по одному элементу ими покрыты всего
строки и столбца, откуда хотя бы в двух произведение
единичное. Итак, неединичных элемента хотя бы
Осталось привести пример
| 1 | 1 | 1 |
| 1 | 2 | 3 |
| 5 | 7 | 1 |
Замечание. Поиск примера проще осуществлять, используя только простые числа и единицы, что здесь и реализуется.
Ошибка.
Попробуйте повторить позже
Каждая клетка таблицы окрашена в один из трех цветов: синий, красный или желтый. При этом в каждой строке таблицы число
красных клеток не меньше числа синих клеток и не меньше числа желтых клеток, а в каждом столбце таблицы число синих клеток не
меньше числа красных клеток и не меньше желтых клеток. Сколько желтых клеток может быть в такой таблице? Приведите пример
соответствующей раскраски.
Источники:
Подсказка 1!
1) Так-с, у нас есть свойство, верное для каждой строки. Давайте попробуем из этого сделать условие для количества клеток разных цветов во всей таблице уже.
Подсказка 2!
2) Да, мы поняли, что во-первых красных не меньше синих во всей таблице, а синих не меньше красных. Что же это значит.........
Подсказка 3!
3) В точности, значит, что их одинаково! А одинаково ли их в каждой строке.... Попробуйте разобраться!
Подсказка 4!
4) А теперь попробуйте доразбираться с точным количеством клеток каждого цвета!
Применяя первое условие для каждой строки, получаем, что красного цвета не меньше, чем синего, и не меньше, чем жёлтого. С другой стороны, из второго условия число синих клеток не меньше, чем желтых и красных. Отсюда число красных равно числу синих.
Пусть в каком-то столбце синих строго больше, чем красных. Тогда во всей таблице их также больше, что невозможно, значит, равенство числа синих и красных выполнено в каждой строке и каждом столбце.
Итак, в каждом столбце по синих и красных (и
жёлтая, иначе жёлтых станет больше, чем других цветов). Отсюда следует, что
жёлтых может быть только
При этом в каждой строке либо по
синих и красных клетки, либо всех цветов поровну, откуда
нетрудно построить пример.
| Ж | Ж | К | К | С | С |
| С | С | Ж | Ж | К | К |
| К | К | С | С | Ж | Ж |
| С | С | К | К | К | С |
| К | К | С | С | С | К |
Ошибка.
Попробуйте повторить позже
Из лампочек собрали табло
Каждая лампочка имеет два состояния — включенное и выключенное. При нажатии на
произвольную лампочку ее состояние сохраняется, а все лампочки, находящиеся с ней в одной строке или в одном столбце,
меняют свое состояние на противоположное. Изначально все лампочки на табло выключены. Петя последовательно нажал на
несколько лампочек, в результате чего табло не погасло полностью. Какое наименьшее количество лампочек может гореть на
табло?
Источники:
Назовём реверсированием набора лампочек смену состояния всех лампочек этого набора на противоположное. Отметим два простых факта.
Нажатие на лампочку эквивалентно реверсированию строки и столбца, в которых эта лампочка стоит. Действительно, при таких
реверсированиях нажимаемая лампочка меняет своё состояние дважды, то есть не меняет его, а остальные лампочки в той же строке и в том
же столбце меняют своё состояние один раз.
При последовательном нажатии нескольких лампочек соответствующие им реверсирования можно производить в любом порядке.
Действительно, для любой лампочки число смен её состояний равно суммарному количеству реверсирований строк и столбцов, которым она
принадлежит.
Пусть было сделано нажатий на лампочки. Припишем
-й строке и
-му столбцу соответственно числа
и
обозначающие
количество их реверсирований. Тогда
Мы можем исключить в левой части чётные и
поскольку чётное число реверсирований строк или столбцов не меняет их
состояния. После этого левая часть останется чётной. С другой стороны, суммы в левой части будут тогда содержать только нечётные
слагаемые. Поэтому число слагаемых в первой сумме (обозначим его через
) имеет ту де чётность, что число слагаемых во второй сумме
(обозначим его через
). Таким образом, мы реверсировали
различных строк и
различных столбов, причём
и
имеют одинаковую чётность. При этом изменяют своё состояние по сравнению с исходным (то есть включатся) в
точности те лампочки, которые стоят в реверсированной строке и нереверсированном столбце или наоборот. Первых лампочек
имеется
а вторых
Поэтому в результате будет гореть
лампочек. Покажем, что
Если
то
чётно и не равно нулю (в противном случае все лампочки будут выключены).
Тогда
Если , то
чётно и не равно нулю (в противном случае все лампочки будут выключены), откуда
Аналогичным образом рассматриваются случаи и
Для дальнейшего заметим, что
для
Поэтому
при
Осталось показать, что можно зажечь ровно лампочки. Для этого достаточно на погашенном табло нажать один раз на
произвольную лампочку.
Ошибка.
Попробуйте повторить позже
В каждой клетке шахматной доски стоит конь. Какое наименьшее число коней можно убрать с доски так, чтобы на доске не осталось ни одного коня, бьющего ровно трех других коней?
Источники:
Будем говорить, что конь контролирует клетку доски, если он бьёт эту клетку или стоит на ней. Докажем вначале, что менее коней
убрать не удастся. Нам достаточно проверить, что с каждой половины доски придётся снять не менее
коней. Рассмотрим для
определённости верхнюю половину и отметим на ней шесть коней так, как показано на рисунке:
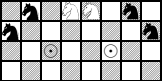
(для удобства они выделены разным цветом). Назовём клетки, отмеченные на рисунке кружочком, кратными, а остальные клетки
простыми. Разобьём рисунок на два квадрата и зафиксируем один из них. Стоящие в квадрате чёрные кони бьют ровно по три
клетки. Поэтому необходимо совершить одно из трёх действий.
Убрать двух коней, стоящих на простых клетках, контролируемых чёрными клетками (ими могут быть и сами чёрные
кони).
Убрать коня, стоящего на кратной клетке. В результате белый конь из этого квадрата будет бить ровно трёх других коней. Значит,
придётся ещё убрать коня с простой клетки, контролируемой белым конём (возможно, самого белого коня).
Те же действия необходимо проделать и для другого квадрата. Таким образом, каждый квадрат определяет пару клеток в верхней половине доски, с которых нужно убрать коней. Эти пары не пересекаются, поскольку никакие два отмеченных коня из разных квадратов не контролируют общих клеток. Иными словами, действия с квадратами производятся независимо друг от друга. Поэтому с верхней половины доски придётся убрать не менее четырёх коней.
Приведём пример, показывающий, что коней достаточно. На рисунке отмечены кони, которых нужно снять с доски.
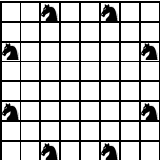
Ошибка.
Попробуйте повторить позже
В театре рядов кресел.
зрителей пришли в театр и расселись по местам (заняв, возможно, не все кресла). После антракта все
зрители забыли, на каких местах они располагались, и сели по-другому. При каком наибольшем
заведомо найдется
зрителя, которые и
до, и после антракта сидели на одном ряду?
Источники:
Если зрители расселись на рядов, то на каком-то ряду оказалось не менее
зрителей (в противном случае на каждом ряду не более
зрителей, а всего их тогда не более
). Так как
нельзя рассадить зрителей этого ряда после антракта так,
чтобы в каждом ряду их оказалось не более трех. Таким образом,
нас устраивает.
Покажем теперь, что при наличии рядов зрителей можно рассадить так, чтобы нужных четырех зрителей не нашлось. Назовем
-й
колонкой места в зале с номером
циклически упорядоченные по рядам:
Пусть циклический сдвиг колонки на рядов — перестановка колонки, при которой новый номер ряда каждого зрителя получается из
старого сдвигом на
позиций вправо в последовательности
Заполним зрителями колонки с номерами от
по
а также первые
мест
-й колонки. Таким образом, в зале окажется
человек. После антракта мы рассадим зрителей следующим
образом. Зрители колонок
садятся на свои места; в колонках
зрители циклически сдвигаются на один ряд, в колонках
— на два ряда, и так далее. В результате мы получим ситуацию, когда нет четырех зрителей, сидевших на одном ряду и до, и после
антракта.
Ошибка.
Попробуйте повторить позже
В клетках таблицы расставлены числа
так, что сумма чисел, расположенных в любом квадратике
не
превосходит
Найдите наименьшее возможное значение
Источники:
Разобьём таблицу на
квадратов
Поскольку сумма чисел во всей таблице равна
среднее арифметическое сумм чисел в этих квадратах равно
Значит, хотя бы в одном квадрате сумма чисел не
меньше
то есть
Пример расстановки, при которой реализуется значение
приведён на рисунке.
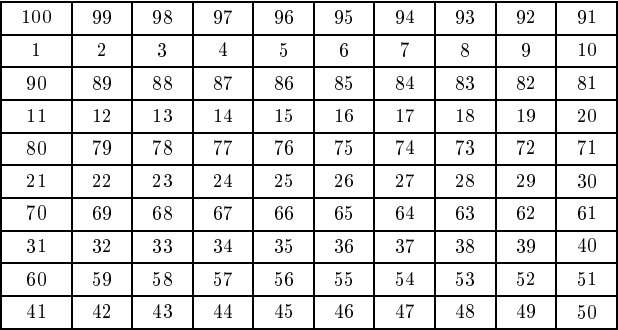
Ошибка.
Попробуйте повторить позже
Какое наибольшее количество различных подмножеств множества можно выбрать так, чтобы любые два различных
выбранных подмножества имели ровно
общих элементов?
Пусть Ясно, что существует ровно
различных подмножеств
содержащих по
элементов, причем
пересечение любой пары таких подмножеств состоит из
элементов. Поэтому ответ задачи не меньше, чем
Докажем обратное
неравенство. Предположим, что нашлись подмножества
удовлетворяющие условию задачи. Тогда верны два
утверждения.
Любое из множеств
содержит не более
элементов. В противном случае найдется множество
совпадающее с
Тогда остальные множества
содержатся в
Поэтому все они состоят из
элементов и, значит, совпадают друг с другом, что
невозможно. Таким образом, каждое из множеств
содержит
или
элементов.
Среди множеств
ровно одно состоит из
элементов. Действительно, хотя бы одно такое множество найдется, поскольку
существует только
подмножеств
из
элементов. С другой стороны, любые два множества, состоящие из
элементов,
совпадают.
Из доказанных утверждений вытекает, что в выбранную систему входят все -элементные подмножества
и некоторое
-элементное подмножество
(например,
). Но не все
-элементные подмножества
содержат
что противоречит
выбору множеств
Ошибка.
Попробуйте повторить позже
Каждый из школьников занимается хотя бы в одной, но не более чем в трех спортивных секциях. Известно, что в каждой секции
состоят один или более школьников и составы любых двух секций различны. Каково максимально возможное количество
секций?
Пусть выбран некоторый максимальный набор секций.
Сделаем два замечания.
Можно считать, что каждый ученик записан в секцию, состоящую только из него. Пусть школьник
таков, что секции
нет.
Выберем какую-нибудь секцию
в которую входит
и заменим ее на
В силу максимальности набора секция
существует.
Каждый школьник по-прежнему занимается хотя бы в одной секции и, значит, новый набор тоже удовлетворяет условиям
задачи.
) Можно считать, что в каждой секции не более двух человек. Пусть нашлась секция
в которую входят школьники
и
Среди них есть двое (например,
и
), не образующих секцию (иначе ученик
был бы участником сразу четырех секций:
и
что невозможно). Тогда заменим
на
В силу максимальности набора секция
существует, потому
новый набор тоже удовлетворяет условиям задачи.
Посчитаем максимальное количество секций с двумя участниками. Каждый ученик входит в не более чем две пары.
Поэтому мы можем отождествить эти пары с набором ломаных на плоскости, вершины которых соответствуют школьникам.
Максимальное число звеньев этих ломаных равно числу вершин, то есть Поэтому в силу
и
общее число секций равно



