Алгебраические текстовые задачи на Ломоносове —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Алгебраические текстовые задачи на Ломоносове

Тема Ломоносов

Алгебраические текстовые задачи на Ломоносове

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ломоносов

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#82783

Старинный подземный ход имеет свод параболической формы (то есть в поперечном сечении туннель ограничен полом — осью $Ox$ и графиком некоторой параболы $2 y = a− bx$ ). Ширина туннеля (измеряется по полу) равна $24$ , высота туннеля равна $18$ . Ход укрепили распорками — на параболе отметили точки $A$ , $B$ , $C$ , $D$ и соединили их между собой балками. Балки $AB$ и $CD$ параллельны полу, $AD$ пересекается с $BC$ , и при этом $∘ ∠ACB = ∠ADB = 90$ . Найдите расстояние между балками $AB$ и $CD$ .

Источники: Ломоносов - 2024, 11.6 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Давайте введем на нашей картинке систему координат, которая была бы нам удобна. К примеру симметричную относительно прямой симметрии параболы и нулевой высоты в тоннеле. Тогда, что нужно чтобы зафиксировать картинку? Каких параметров будет достаточно, чтобы выразить через это всю картинку?

Подсказка 2

Нам достаточно h - высоты вершины, а также длины основания - 2l(для симметрии). Тогда, если наша парабола задается функцией f(x) = a - bx^2, то f(l) = f(-l), f(0) = h. Тогда f(x) = h(1 - x^2/l^2). Значит, мы можем задать две точки A и C, а остальные - будут отличаться от симметричных только умножением на -1 абсциссы. Давайте так и сделаем - пусть x_1 - абсцисса А, а x_2 - абсцисса C. Тогда как нам выразить перпендикулярность, если мы работаем в координатах? Мы ведь не использовали еще ни разу тот факт, что, к примеру, AC и CB перпендикулярны.

Подсказка 3

Верно, мы можем выразить это через скалярное произведение векторов AC и CB. После того, как мы запишем и преобразуем выражение, у нас получится, что -(x_2^2 - x_1^2) - (h^2)/(l^4) * (x_2^2 - x_1^2)^2 = 0. Но при этом, у нас x_1 != x_2, поэтому x_2^2 - x_1^2 = - (h^2)/(l^4). Тогда, нам остается понять, чему равно расстояние между балками и записать ответ!

Показать ответ и решение

Обозначим ширину тоннеля за $2l$ , а высоту за $h$ . Из этих параметров однозначно выводятся параметры параболы: $x$ принадлежит отрезку $[−l,l],$ а $y(l)= y(−l)= 0,$ так что

hx2 y(x)= h− -l2-

Теперь зададим координаты точек так:

2 2 2 2 A = (x1,h(1− xl12 )),B = (−x1,h(1 − x1l2 )),C = (x2,h(1 − x2l2 )),D = (x2,h(1− x2l2 ))

Так как $AB$ и $CD$ параллельны полу, то понятно, что ординаты $A$ и $B$ одинаковы. Значит, абсциссы отличаются только знаком. Аналогично для $C$ и $D$ .

$PIC$

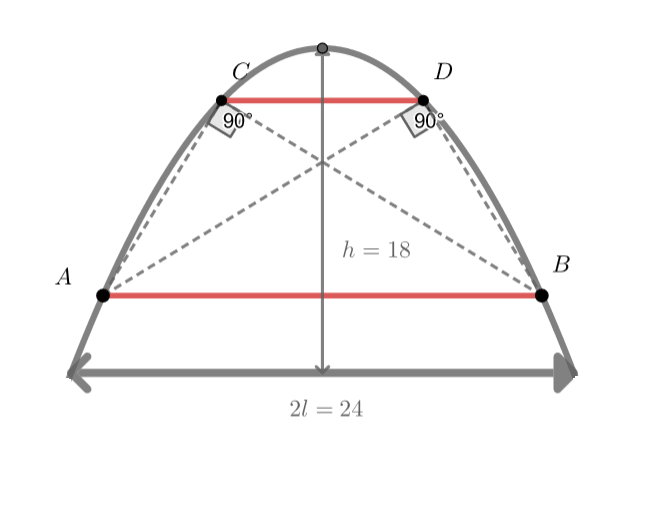
Тогда перпендикулярность $AC$ и $CB,$ $AD$ и $DB$ можно выразить, например, через равенство нулю скалярных произведений. Достаточно рассмотреть одну пару, так как рисунок симметричен.

AC = (x2− x1; h(x2− x2),CB = (−x1 − x2; h(x2− x2)) l2 1 2 l2 2 1

2 2 h2- 2 22 AC ⋅CB =− (x2− x1)− l4 (x2− x1)= 0

Тогда либо $2 2 (x2− x1) =0$ (но балки не совпадают, поэтому такой вариант не подойдет), либо

2 2 l4 (x2− x1)= − h2

А расстояние между балками это:

2 |hl2(x22− x21)|= lh-= 8

Ответ: 8

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#82781

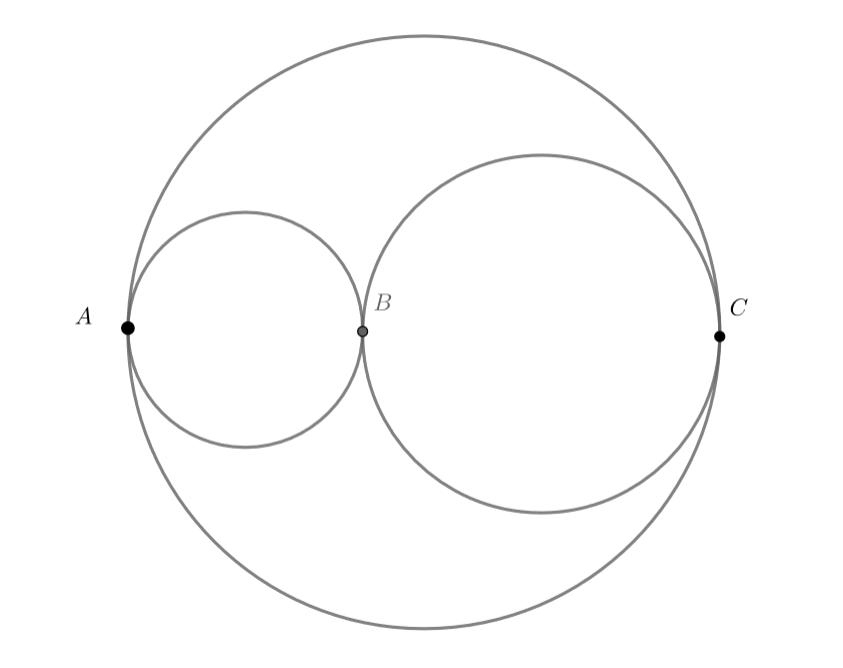
Автодром состоит из трех попарно касающихся кольцевых трасс (две окружности касаются друг друга попарно в точке $B$ внешним образом и третьей в точках $A$ и $C$ внутренним, причём $AC$ — диаметр третьей окружности). Автомобиль в любой точке касания может продолжать движение по любой из двух возможных трасс, но нигде не может разворачиваться на $∘ 180$ . По каждой из трех трасс автомобиль едет со своей скоростью, так что любую из двух $AB$ длиной $15$ км он проезжает за $7$ минут, любую из дуг $BC$ длиной $25$ км — за $11$ минут, а любую из дуг $AC$ — за $17$ минут. Выехав из точки $A$ , автомобиль через $1$ час $25$ минут оказался в ней же. Сколько километров проехал автомобиль?

$PIC$

Источники: Ломоносов - 2024, 11.4 (см. olymp.msu.ru)

Показать ответ и решение

Рассмотрим варианты, которыми находящийся в точке $A$ автомобиль может в следующий раз впервые снова оказаться в этой точке.

Во-первых, можно сделать это, не проходя через точку $C$ , т. е. путем $ABA$ .

Во-вторых, можно одним из двух способов ( $AC$ или $ABC$ ) добраться до точки $C$ , сделать несколько кругов $CBC$ («несколько» может быть и нулем) и вернуться одним из двух способов ( $CA$ или $CBA$ ) в точку $A$ .

В любом случае мы либо четное число раз проезжаем по 7-минутной дуге, четное число раз по 11-минутной и четное число раз по 17 -минутной, либо наоборот, нечетное число раз по каждому из трех типов дуг.

То же самое можно сказать про неоднократное возвращение в точку $A$ .

«Четный» случай нам не подходит, так как по условию на каждую дугу уходит целое число минут, а общее время выражается в минутах нечетным числом. Заметим, что любая тройка нечетных положительных чисел может быть реализована в качестве числа проходов (в любом направлении) дуг $AB$ , $BC$ , $AC$ .

Действительно, выехав из точки $A$ и сделав заданное нечетное число проходов $AB$ , мы окажемся в точке $B$ , после чего, сделав заданное нечетное число проходов $BC$ , мы окажемся в точке $C$ , а после заданного нечетного числа проходов $AC$ — снова в точке $A$ .

Итак, попробуем найти три таких нечетных положительных числа $i$ , $j$ , $k$ , что

7i+11j+17k= 60+ 25= 85

Для $k$ возможны $3$ варианта: $5,3,1.$ Первый случай отбрасываем, так как для него получаем $i= j =0.$

Во втором случае имеем $7i+ 11j = 34$ . Если $j ≥ 3$ , то $i< 1.$ При $j = 1$ число $34− 11⋅1 =23$ не делится на $7$ .

Наконец, при $k= 1$ имеем $7i+ 11j =68$ . Для $j =5,3,1$ получим $7i=13,35,57$ , откуда $j = 3,$ $i= 35:7= 5,$ а пройденный путь равен $15⋅5+ 25⋅3+ 40⋅1= 190(км).$ Здесь $40= 15+ 25$ — длина дуги $AC$ , которую находим геометрически:

AC = πR= π(r1+ r2)=πr1+ πr2 = AB+ BC,

где $R,r1,r2$ — радиусы.

Ответ: 190

Ошибка.
Попробуйте повторить позже

Задача 3#70491

Если действительные числа $a,b,c$ упорядочить по нестрогому возрастанию, получив тройку $x ≤x ≤ x , 1 2 3$ то число $x 2$ будем называться средним из чисел $a,b,c.$ Найдите все значения $t,$ при каждом из которых среднее из трёх чисел

3 t 1 a= t − 100t; b= 2− 16; c= sint− 2

положительно.

Источники: Ломоносов-2022, 11.5 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Среднее из трёх чисел положительно, а числа заданы с параметром да еще и в виде функций... Сравнивать такие числа реально сложно, надо подумать, как можно переформулировать вопрос.

Подсказка 2

Если рассуждать в общем, то для того, чтобы среднее из трех чисел было положительно, среди них должно быть не менее двух положительных, иначе условие задачи не выполниться (два числа будут неположительными, а среднее по нестрогому возрастанию уж точно!)

Подсказка 3

То есть нам подойдут случаи, когда два или три числа положительны. Теперь поймем, когда же наши числа будут положительными = найдем нули функций и отметим их на вещественной прямой.

Подсказка 4

Сначала можно отметить нули чисел(функций) a и b, так как кол-во их нулей конечно, расставить знаки функций на каждом промежутке и заметить, что некоторые промежутки нам уже подходят, а некоторые - точно нет.

Подсказка 5

Осталось понять знаки числа(функции) с, это можно сделать только на уже потенциально подходящих нам промежутках, выписать их объединение в ответ.

Показать ответ и решение

Напрямую значения $a,b,c$ сравнивать сложно. Однако, чтобы среднее из трёх чисел было положительным, необходимо и достаточно, чтобы по крайней мере два числа из тройки были положительны.

3 a= t − 100t= t(t− 10)(t+ 10)> 0⇒ t ∈(−10;0)∪ (10;+ ∞)

t b= 2 − 16> 0⇒ t> 4

( ) c= sint− 1> 0⇒ t∈ 2πn+ π;2πn+ 5π , где n ∈ℤ 2 6 6

Нужно, чтобы хотя бы два из трех чисел были положительны. $a> 0$ и $b> 0$ при $t> 10,$ область $(10;+∞ )$ идёт в ответ. $a≤ 0$ и $b≤ 0$ при $t∈(−∞;− 10]∪ [0;4],$ эта область в ответе быть не может. На оставшейся области $t∈ (− 10;0)∪(4;10]$ положительно только одно из чисел $a,b.$ Значит, в ответ пойдут те её части, где $c> 0.$ Посмотрим, как пересекаются

( π 5π ) t∈(−10;0)∪ (4;10] и t∈ 2πn+ 6;2πn + 6 , где n ∈ℤ

При $n =0$ получим интервал $( ) t∈ π6;5π6 .$ Он с областью $t∈(−10;0)∪ (4;10]$ не пересекается, ведь $0< π6 < 5π6-< 4.$

При $n =1$ получим интервал $( ) t∈ 2π+ π6;2π+ 56π .$ Он лежит в области целиком, ведь $4< 2π+ π6 <2π + 5π6 <10.$ Интервал идёт в ответ.

При $n =− 1$ получим интервал $t∈ (− 2π + π6;− 2π + 5π6 ).$ Он тоже лежит в области целиком, ведь $− 10< −2π+ π6 <− 2π + 5π6-< 0.$ Интервал идёт в ответ.

При $n =− 2$ получим интервал $( π 5π-) t∈ − 4π+ 6;−4π+ 6 .$ Тут получается такое неравенство: $π 5π − 4π+ 6 < −10< −4π+ 6 ,$ интервал пересекается с областью $t∈ (−10;0)∪(4;10],$ пересечение - это множество $( 5π) −10;− 4π + 6 ,$ которое пойдёт в ответ.

При остальных $n$ интервалы заведомо лежат либо далеко левее $− 10,$ либо правее $10,$ и на ответ не повлияют.

В итоге ответ складывается из объединения множеств

( π 5π) ( π 5π) ( 5π) (10;+∞ ), 2π+ 6;2π+ 6- , − 2π + 6;−2π+ 6- , −10;−4π+ -6

Ответ:

$(− 10;−4π+ 5π)∪(−2π + π ;− 2π + 5π)∪ (2π + π;2π + 5π)∪ (10;+∞ ) 6 6 6 6 6$

Ошибка.
Попробуйте повторить позже

Задача 4#47235

Из поселка на станцию по одной дороге одновременно отправились дачник А пешком и мотоцикл с пассажиром - дачником Б. Не доехав до станции, мотоциклист высадил пассажира и сразу поехал обратно к поселку, а дачник Б пошел к станции пешком. Встретив дачника А, мотоциклист посадил его к себе и привез на станцию. В результате оба дачника прибыли на станцию одновременно. Какую часть пути от поселка до станции дачник А проехал на мотоцикле, если дачники шли с одинаковой скоростью, в $9$ раз меньшей скорости мотоцикла?

Источники: Ломоносов-2019, 11.1 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Если дачники отправились и прибыли одновременно, могли ли они проехать на мотоцикле разную долю пути?

Подсказка 2

Подумайте, сколько проехал мотоциклист прежде, чем забрал дачника А? Для удобства, можно ввести переменную на долю пути, которую прошел дачник самостоятельно.

Подсказка 3

А что можем сказать о времени, затраченном на путь мотоциклистом и дачником А до их встречи? Составьте уравнения, используя условие на скорости и найденные расстояния и вычислите все нужные величины!

Показать ответ и решение

Первое решение.

Пусть расстояние от посёлка до станции равно $1$ . Если какой-то из дачников ехал на мотоцикле дольше другого, то он должен был преодолеть большее расстояние (меньше перемещаясь пешком), поскольку их скорости пешком равны. Значит, дачники ехали на мотоцикле (и шли пешком) одинаковое время. Пусть каждый прошёл $x$ , тогда мотоциклист высадил дачника Б в точке $1− x$ , считая от посёлка, а затем забрал дачника А в точке $x$ , проехав до неё $1− x− x= 1− 2x$ . Отсюда суммарно до встречи с дачником А мотоцикл проехал расстояние $1− x+ 1− 2x =2 − 3x$ , за это время сам дачник прошёл $x$ . Из условия на скорости выполнено соотношение

1 2− 3x= 9⋅x ⇐⇒ x= 6

Отсюда на мотоцикле каждый дачник проехал $56$ пути.

Второе решение.

$PIC$

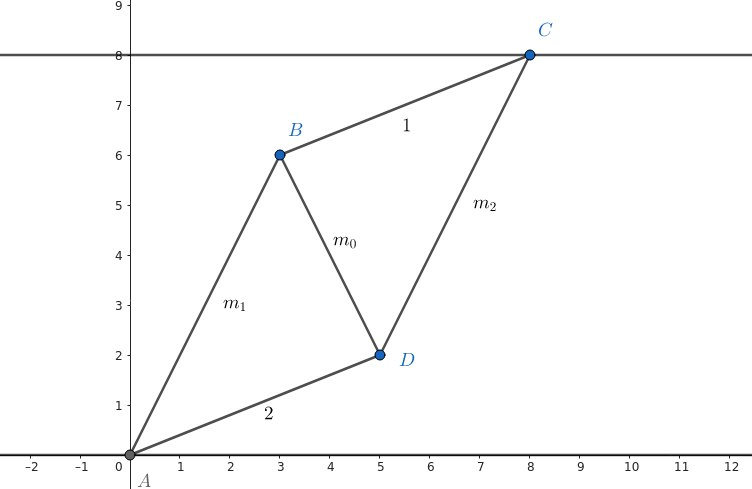
Будем решать задачу графически. Условие про скорость в девять раз больше будет означать в 9 раз больший коэффициент наклона (на графике приблизительно, чтобы никого не шокировать чертежом). Пусть первый дачник следовал по маршруту $ABC$ , мотоциклист — по $ABDC$ , второй дачник — по $ADC$ . Из равных скоростей дачников следует, что $AD ∥BC$ , из одинаковой скорости мотоциклиста $AB ∥CD$ , значит, $ABCD$ — параллелограмм, откуда мотоциклист проехал с каждым дачником одно и то же расстояние и каждый дачник прошёл одно и то же расстояние. Пусть каждый дачник шёл пешком часть пути $r∈ [0,1]$ , тогда мотоциклист вёз каждого из них часть $1− r$ , при этом кусочек $m0$ является частью пути $1− r− r =1 − 2r$ . Тогда пока второй дачник шёл $r$ , мотоциклист проехал $m0+ m1$ , получаем соотношение $1 m1+ m0 =1− r+ 1− 2r =2 − 3r= 9⋅r⇐⇒ r= 6$ .

Ответ:

$5 6$

Ошибка.
Попробуйте повторить позже

Задача 5#78229

Архив фотографий укладывают в порядке их нумерации в одинаковые альбомы, ровно по 4 фотографии на одну страницу. При этом 81-я по счёту фотография попала на 5-ю страницу одного из альбомов, 171-я — на 3-ю страницу другого. Сколько фотографий вмещает каждый альбом?

Источники: Ломоносов - 2018. 11.4 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Сложность нам добавляет то, что мы не знаем сколько альбомов и под какими номерами эти альбомы. Давайте обозначим их за x и y. x < y., а кол-во страниц на них за n. Каким условием можно задать то, что фотография с таким-то номером попала в альбом с номером x? А на такую-то страницу альбома x?

Подсказка 2

Это значит, что все предыдущие альбомы уже заполнены, а в этом альбоме - все предыдущие страницы уже заполнены. Но еще это значит, что номер этой фотографии точно не больше, чем кол-во фотографий в предыдущих альбомах и на этой странице! Как это записать алгебраически?

Подсказка 3

Вот пример условия для 81ой фотографии: 4n(x-1) + 4*(5-1) < 81 ≤ 4n(x-1) + 4*5. Запишите эти неравенства и дальше дорешайте задачку)

Показать ответ и решение

Пусть $x,y$ — номера альбомов, в которые попали $81−$ я и $171−$ я фотографии соответственно, $n >4$ — количество страниц в альбоме. Тогда

4n(x − 1)+ 16 <81≤ 4n(x − 1)+ 20⇒ 61≤ 4n(x− 1)< 65

4n(y− 1)+ 8< 171 ≤4n(y− 1)+ 12⇒ 159≤ 4n(y− 1)<163

Тогда

n(x− 1) =16, n(y− 1)= 40

Из первого неравенства следует, что $n$ может быть равно $1, 2, 4, 8, 16,$ из второго неравенства — $1, 2, 4, 5, 8, 10, 20, 40.$ Таким образом, $n =8, 4n =32.$

Ответ: 32

Ошибка.
Попробуйте повторить позже

Задача 6#47039

На каком из пяти интервалов, на которые разбивают числовую ось четыре точки

5 8 2 6 x < y <y < x ,

лежит число $0?$

Источники: Ломоносов-2018, 11.1 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Посмотрев на степени, на их чётность, можно сузить количество вариантов ответа) Какие ограничения можно наложить на буквы, сравнив степени между собой и посмотрев на знак неравенства?

Подсказка 2

Т.к. степени четные, можно предположить, что y>0. Тогда, т.к. y⁸<y⁵ ⇒y∈(0;1). А как разобраться с x?

Подсказка 3

Разберем 2 случая: x<0 и x>0. Тогда, посмотрев на знаки неравенств, можно сделать выводы и решить задачу!

Показать ответ и решение

Не умаляя общности, можно считать, что $y > 0$ (равенства быть не может). Отсюда $y ∈ (0,1)$ . Далее всё зависит от знака $x$ .

Если $x> 0$ , тогда $x >1$ , но при таком условии $5 x$ не может быть наименьшим из чисел. так что этот случай невозможен.

Если $x< 0$ , то вполне подойдёт $x= −1$ , тогда $0$ лежит на интервале $5 8 (x ,y )$ .

Ответ:

$(x5,y8)$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#83946

Том Сойер, Сид Сойер и Гек Финн красили забор. Вначале Том красил один в течение времени, за которое Сид и Гек, работая вместе, могли бы покрасить половину забора. Затем красил один Сид в течение времени, за которое Том и Гек, работая вместе, могли бы покрасить $5 4$ всего забора. Потом красил один Гек в течение времени, за которое Том и Сид работая вместе, могли бы покрасить четверть всего забора. В результате забор был покрашен. Во сколько раз быстрее они окончили бы работу, если бы с самого начала все время работали вместе? (Предполагается, что скорость работы каждого мальчика постоянна.)

Показать ответ и решение

Обозначим через 1 всю работу по окраске забора, через $x,y$ и $z$ производительность Тома, Сида и Гека соответственно, а через $t,t,t 1 2 3$ - промежутки времени, в которых Том, Сид и Гек соответственно работали по одному. Тогда, по условию,

1 5 1 (y+ z)t1 = 2, (x+ z)t2 = 4, (x+ y)t3 = 4, xt1+ yt2+ zt3 =1.

При этом найти нужно величину $(t1+ t2+t3)$ :

1 x+-y+-z = (x+ y+z)(t1+ t2+t3).

Раскрывая скобки, получим

xt1+ (y+ z)t1+yt2+ (x+ z)t2+ zt3+ (x+ y)t3 = 1+ 1+ 5+ 1 =3 2 4 4

Ответ: в 3 раза

Ошибка.
Попробуйте повторить позже

Задача 8#31288

Незнайка прыгал от своего дома к дому Знайки. Три четверти пути он пропрыгал прыжками, длина которых равна двум его обычным шагам, а остальную четверть пути — прыжками, длина которых равна трем его обычным шагам. Оказалось, что прыжков в два шага оказалось на $350$ больше, чем прыжков в три шага. Сколько обычных шагов от дома Знайки до дома Незнайки? Считаем, что все шаги у Незнайки одинаковые.

Источники: Ломоносов-2016, 11.1 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Введем переменные, и составим уравнение.

Подсказка 2

По условию Незнайка пропрыгал двойными прыжками в три раза больше, чем тройными. Из этого условия можно получить уравнение, и найти x

Подсказка 3

Нам необходимо найти расстояние в шагах от дома Знайки до дома Незнайки.

Показать ответ и решение

Пусть Незнайка сделал $x$ прыжков по $2$ шага, $x − 350$ — по $3$ . Тогда $2x= 3⋅3(x− 350)$ , то есть $7x= 9⋅350=⇒ x= 450$ , а значит, всего шагов $2x +3(x− 350)= 900 +300= 1200$ .

Ответ:

$1200$

Ошибка.
Попробуйте повторить позже

Задача 9#67154

Два поезда, содержащие по $15$ одинаковых вагонов каждый, двигались навстречу друг другу с постоянными скоростями. Ровно через $28$ с после встречи их первых вагонов пассажир Саша, сидя в купе третьего вагона, поравнялся с пассажиром встречного поезда Валерой, а еще через $32$ с последние вагоны этих поездов полностью разъехались. В каком по счету вагоне ехал Валера?

Подсказки к задаче

Подсказка 1

Очень удобно, что в условии поезда полностью одинаковы. Значит, несложно представить, как взаимодействуют вагоны поезда. Также обратим внимание, что же случилось с поездами в конце всех описанных в условии действий. О чём это говорит?

Подсказка 2

Заметим, что вагоны разъезжались попарно(первый с первым, второй со вторым), а с момента встречи первых вагонов до момента разъезда последних вагонов прошло 60 минут. Что тогда произошло ровно через 28 секунд?

Подсказка 3

Разъехались седьмые вагоны, т.к. через каждые 60:15=4 секунды разъезжались очередные вагоны. Значит, седьмой вагон одного поезда сравнялся с восьмым вагоном второго поезда! Осталось аккуратно посчитать, какой вагон встретил Валера)

Показать ответ и решение

Так как с момента встречи их первых вагонов до момента разъезда последних вагонов прошло $60$ секунд, то, так как вагоны одинаковые, через каждые $60:15= 4$ секунды разъезжались очередные вагоны. Поэтому через $28$ секунд разъехались седьмые вагоны поездов, то есть седьмой вагон одного поезда поравнялся с восьмым вагоном другого. В этот момент третий, Сашин, вагон поравнялся с Валериным вагоном, имеющим номер $8+ (7 − 3)= 12.$

Ответ:

$12$

Ошибка.
Попробуйте повторить позже

Задача 10#43621

Из пунктов $A$ и $B$ навстречу друг другу одновременно отправились два поезда. Известно, что в $14 :00$ они встретились и, не меняя скорости, продолжили движение. Один поезд прибыл в пункт $B$ в $18:00$ , а другой прибыл в пункт $A$ в $23:00$ . В какой момент времени поезда отправились в путь?

Источники: Ломоносов-2012

Показать ответ и решение

Пусть поезда отправились за $t$ часов до момента встречи, и пусть $v 1$ - скорость первого поезда, $v 2$ - скорость второго. Тогда первый поезд прошёл расстояние $tv1$ от пункта $A$ до пункта встречи со вторым поездом, а второй поезд прошёл это же расстояние (после встречи с первым поездом) за 9 часов, поэтому $tv1 = 9v2$ . Аналогично второй поезд прошёл расстояние $tv2$ от пункта $B$ до пункта встречи, а первый поезд затем прошёл это расстояние за $4$ часа, поэтому $tv2 =4v1.$ Перемножая эти два уравнения, получим

tv1⋅tv2 =9v2⋅4v1 ⇒ t2 =36 ⇒ t=6

Итак, поезда отправились в путь за $6$ часов до $14:00$ , т. е. в $8 :00.$

Ответ:

$8 :00$

Ошибка.
Попробуйте повторить позже

Задача 11#80196

На доске написан квадратный трёхчлен $x2 +9x+ 47$ . Таня (по своему усмотрению) увеличивает или уменьшает на 1 коэффициент при $x$ , после чего Ваня увеличивает или уменьшает на фиксированное число $m$ свободный член, а далее эти действия повторяются. Как только написанный на доске многочлен имеет целый корень, Ваня получает оценку «пять». Может ли он обеспечить себе «пятёрку» при любых действиях Тани, если

(a) $m =2?$

(b) $m =3?$

Подсказки к задаче

Пункт а, подсказка 1

За значением в какой точке x_0 несложно наблюдать, если Таня увеличивает или уменьшает значение многочлена на x_0? Какое значение у многочлена в этой точке сейчас и какие действия должен сделать Ваня, чтобы максимально приблизить его к 0?

Пункт а, подсказка 2

Рассмотрим значение f(x) = x^2 + 9x + 47 в точке 1. Какое оно сейчас? Как может действовать Ваня и насколько сильно можно приблизить значение f(1) к нулю?

Пункт а, подсказка 3

Ваня может всегда уменьшать f(1) и сделать так, чтобы -1 <= f(1) <= 1. Осталось лишь рассмотреть ходы Тани после этого и придумать ответные действия!

Пункт б, подсказка 1

Можно попробовать поиграть за наших героев и подставлять различные иксы. Что можно заметить? Какова связь с нашим m? Может ли обнулиться значение? Найдем какой-нибудь инвариант.

Пункт б, подсказка 2

Обратите внимание, что Ваня своими действиями не влияет на делимость многочлена на 3. А что делать Тане, чтобы не допустить кратности трём?..

Показать ответ и решение

(a) Пусть $f(x)=x2+ 9x+ 47.$ Ваня сможет за конечное количество ходов добиться $f(1)= 0.$ Вначале $f(1)= 1+9 +47= 57.$

Далее каждым своим ходом Ваня может уменьшать $f(1)$ и добиться, чтобы (после его хода) $− 1≤ f(1) ≤1.$ Если Таня сделает $f(1)$ равным нулю (или оно уже равно нулю), то Ваня сразу выиграл.

Иначе Таня вынуждена сделать $f(1) =− 2$ или $f(1)=2$ и опять-таки Ваня выигрывает.

(b) Стратегия Тани — держать коэффициент при $x$ равным 10 или 11.

В этом случае значение многочлена $f(x)$ будет не кратно трем и, следовательно, не равно нулю.

Действительно, многочлены

f(x)= x2+10x+ 2+ 3k и f(x)= x2+11x+ 2+ 3k

не кратны трем при любом целом $x.$

При $x= 3n$ остаток от деления $f(x)$ на три равен 2; при $x= 3n+ 1$ остаток от деления $f(x)$ на три составляет 1 и 2, соответственно; при $x = 3n +2$ остаток от деления $f(x)$ на три составляет 2 и 1, соответственно.

Ответ:

(a) да

(b) нет

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#77820

В свежих грибах содержание воды колеблется от $80%$ до $99%$ , а в сушёных — от $20%$ до $40%$ . В какое наибольшее число раз при этих ограничениях может уменьшиться вес грибов в результате сушки?

Источники: Ломоносов - 2009, 11 (см. olymp.msu.ru)

Подсказки к задаче

Подсказка 1

Процент содержания воды - это процент веса воды в этом грибе) Давайте обозначим за x вес сухой части гриба. Как можно выразить вес гриба до и после сушки?

Подсказка 2

Если у нас есть какой-то процент содержания воды, например k%, то значит, что сухая часть - это (100-k)% от веса гриба. Найдите из этого вес гриба до/после сушки и максимум отношения весов до и после сушки)

Показать ответ и решение

Пусть $x$ — вес сухой части грибов, $a%$ — содержание воды в свежих грибах, $b%$ — в сушёных.