Геометрия помогает алгебре —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Геометрия помогает алгебре

Тема АЛГЕБРА

Геометрия помогает алгебре

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Разделы подтемы Геометрия помогает алгебре

Задачи на движение: графический подход

Увидеть расстояние между точками

Увидеть треугольник

Увидеть векторы

Геометрическая вероятность

Подтемы раздела алгебра

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#85996

Для положительных чисел $x,y,z$ докажите неравенство

∘-2------2- ∘ -2------2 ∘-2-------2 x − xy+ y + y − yz+ z ≥ z + zx+ x

Показать доказательство

Отложим от одной точки на плоскости отрезки длиной $x,y,z$ так, чтобы угол между отрезками $x$ и $y$ был $60∘,$ угол между отрезками $y$ и $z$ был $∘ 60,$ а угол между отрезками $x$ и $z$ был $∘ 240 .$ Обозначим вторые концы отрезков $x,y,z$ через $A,B$ и $C$ соответственно. Тогда по теореме косинусов $∘ -2------2- ∘ -2------2 √ 2-------2- AB = x − xy+y ,BC = y − yz+z ,CA = z +zx+ x .$ Тогда наше неравенство сразу следует из неравенства треугольника $ABC$ (возможно, вырожденного).

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#83742

Даны числа $x,y,z$ такие, что

x 4 6 4 + sin y+ ln z = 16

Докажите, что

x+1 2 3 2 + 3sin y− 6ln z ≤ 28

Источники: Звезда - 2024, 11.3 (см. zv.susu.ru)

Подсказки к задаче

Подсказка 1

Тригонометрия, логарифм и показательная функция в одном месте — вряд ли мы здесь обойдёмся банальными преобразованиями. Видно только, что первое выражение, равное 16, — сумма трёх квадратов каких-то величин, а во втором выражении стоят похожие величины, но без квадратов. Какие есть неравенства, связывающие такие суммы?

Подсказка 2

Неравенство Коваля-Белова-Шурыгина! Ой, то есть Коши-Буняковского-Шварца) Ну то самое про квадрат суммы и сумму квадратов. Говоря по простому, это факт, что скалярное произведение не больше произведения длин (это же и так понятно, да?..) Давайте соорудим векторы с нужными координатами!

Подсказка 3

Компоненты первого вектора — величины, сумма квадратов которых равна 16. А второй вектор нужно подобрать так, чтобы их скалярное произведение выглядело как то выражение, которое не должно превосходить 28. Пробуйте!

Показать доказательство

Используем неравенство КБШ в векторном виде. Рассмотрим векторы $⃗a= (2x;sin2y;ln3z)$ и $⃗b= (2;3;−6).$ Скалярное произведение

x+1 2 3 ⃗a ⋅⃗b =2 + 3sin y− 6ln z ≤ |⃗a|⋅|⃗b|

Имеем

⃗ √-------- |b|= 4+ 9+ 36 =7

|⃗a|= ∘4x+-sin4y+-ln6z =4

Тогда получаем, что

2x+1+ 3sin2y− 6ln3z ≤ 28

Ошибка.
Попробуйте повторить позже

Задача 3#79605

Наименьшее значение функции

∘ -2---2 ∘ -2--2- ∘ -2--2- ∘ -2-------2 x1+ 1 + x2+ 2 + x3+ 3 +...+ x2024+2024

для неотрицательных $x1,x2,...,x2024$ , сумма которых равна $k$ , равно $2024⋅2025$ . При каком значении параметра $k$ такое возможно?

Источники: ОММО - 2024, задача 7 (см. olympiads.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте внимательнее посмотрим на задачу и попробуем вспомнить хитрый способ решения неравенств, нахождения минимума или максимума. Напоминают ли вам что-то квадратные корни из суммы квадратов? Где вы такое могли видеть?

Подсказка 2

Давайте ещё подумаем, чтобы не сразу раскрывать вам все "секреты". Могли ли вы встречать подобное в геометрии? Может быть это длина какого-то отрезка?

Подсказка 3

Верно, это же теорема Пифагора, где числа под корнями являются катетами прямоугольного треугольника. Как же теперь можно проиллюстрировать нашу задачу?

Подсказка 4

Да, получается мы можем расположить отрезки с иксами вдоль одной прямой, а с числами вдоль перпендикулярной ей. В итоге, у нас получится ломанная. Понятно, что минимумом будет просто расстояние между крайними точками ломанной, а это гипотенуза с катетами из суммы наших катетов. Осталось понять, что мы знаем обе суммы и из условия про минимум найти k, решив уравнение. Победа!

Показать ответ и решение

На оси абсцисс отметим отрезки, равные по длине $x,x ,...,x 1 2 2024$ , а на оси ординат — отрезки длины $1,2,...,2024$ . Тогда выражение $∘ -2--- x1+1$ — это расстояние от точки $(0,0)$ до точки $(x1,1)$ , а $∘ 2---2- x2 +2$ — расстояние от точки $(x1,1)$ до точки $(x2+ x1,3)$ .

$PIC$

Таким образом, получили ломанную из точки $(0,0)$ до точки с координатами

$(x1+ ...+ x2024,2024⋅22025) =(k,2024⋅22025)$ . Ее длина не превосходит расстояния между этими точками, то есть

( ) ∘x2-+12+ ∘x2-+22+ ∘x2+-32+ ...+ ∘x2--+-20242 ≥ 2024⋅2025 2+k2 1 2 3 2024 2

Тогда

∘ (--------)2---- 2024⋅2025= 2024⋅2025 + k2 2

Решив это уравнение, находим

√3 k = 2-⋅2024 ⋅2025

Ответ:

$2025⋅1012√3$

Ошибка.
Попробуйте повторить позже

Задача 4#75238

Даны $8$ ненулевых вещественных чисел $a,a ,...,a . 1 2 8$ Докажите, что по крайней мере одна из шести сумм $a1a3+ a2a4,a1a5+ a2a6,a1a7 +a2a8,a3a5+a4a6,a3a7+ a4a8,a5a7+ a6a8$ неотрицательна.

Показать доказательство

Пусть векторы $v,v ,v ,v 1 2 3 4$ в прямоугольной системе координат имеют координаты $(a,a ),(a,a ),(a,a ),(a,a ) 1 2 3 4 5 6 7 8$ соответственно. Тогда среди указанных сумм встречаются значения всевозможных скалярных произведений двух векторов из набора $(v1,v2,v3,v4).$

Скалярное произведение двух векторов отрицательно тогда и только тогда, когда угол $α$ между этими векторами является тупым. Таким образом, достаточно показать, что среди любых четырех векторов в двумерном пространстве найдутся два, угол между которыми не превосходит $∘ 90.$

Предположим противное, тогда каждый из направленных углов $∠(v1,v2),∠(v2,v3),∠(v3,v4),∠(v4,v1)$ больше $∘ 90$ (без ограничений общности считаем, что каждый из углов принимает положительное значение). Следовательно, их сумма больше $∘ 360.$ C другой стороны,

∠(v1,v2)+ ∠(v2,v3)+ ∠(v3,v4)+ ∠(v4,v1)=360∘

тем самым получено противоречие.

Ошибка.
Попробуйте повторить позже

Задача 5#74141

Пусть $a,b,c$ — стороны треугольника. Докажите неравенство:

2 2 2 a b(a− b)+b c(b− c)+c a(c− a)≥0.

Показать доказательство

Сделаем стандартную для сторон треугольника замену: $x = a+b,y = b+c,z = a+ c.$ Раскроем скобки и сократим подобные слагаемые. Получим, что нужно доказать следующее:

3 3 3 x y+ y z+z x≥ xyz(x +y+ z)

Но заметим, что по неравенству о средних:

3 3 3 2 4xz+ 2y x+z y ≥ 7x yz

Аналогично, для $2$ других слагаемых правой части, после сложения $3$ неравенств получим требуемое.

Ошибка.
Попробуйте повторить позже

Задача 6#74139

Существует ли треугольник со сторонами $x$ , $y$ и $z$ такой, что

3 3 3 x + y +z = (x+ y)(y+ z)(z+ x)?

Показать ответ и решение

Сделаем стандартную для сторон треугольника замену: $x = a+b,y = b+c,z = a+ c.$ Раскроем скобки и сократим подобные слагаемые. Получим, что должно выполнятся равенство $0 =6abc.$ Что невозможно, значит такого треугольника не существует.

Ответ:

Не существует

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#74137

Положительные $a,b,c$ удовлетворяют условию $abc(a+b+ c)= 3.$ Докажите, что $(a+b)(a +c)(b+ c)≥8.$

Показать доказательство

Давайте сделаем следующую замену: $a +b= x,b+c =y,a+ c= z.$ А также обозначим полупериметр треугольника со сторонами $x,y,z$ (а такой существует, так как очевидно, что выполняется неравенство треугольника) за $p.$ Тогда условия перепишутся следующим образом:

p(p− a)(p− b)(p − c)= 3

xyz ≥8

Первое условие говорит нам о том, что площадь треугольника $S = √3$ по формуле Герона. Значит имеет место быть равенство: $xyz= √3. 4R$ Тогда можно переписать вопрос как: $R ≥ √2. 3$ Предположим противное, $R< √2, 3$ тогда по известному факту о том, что при фиксированном радиусе треугольник наибольшей площади — равносторонний можем понять (чтобы его доказать, можно заметить, что для фиксированной стороны треугольник наибольшей площади равнобокий, значит он равнобокий для всех $3$ сторон-оснований), что наибольшая площадь будет равна $3√3R2< √3 =S. 4$ Противоречие.

Ошибка.
Попробуйте повторить позже

Задача 8#73449

Положительные числа $a,b,c$ удовлетворяют соотношению

2 2 2 a +b + c =1

Найдите наибольшее возможное значение выражения $ab+ bc√3.$

Показать ответ и решение

Первое решение.

Из условия имеем

(| 2 2 2 ||{a + b+ c = 1 ||a,b,c> 0 |(ab+bc√3→ max

Рассмотрим вспомогательные векторы на плоскости с координатами $√- ⃗x =(a,c);⃗y = (12b,-32 b)$ . Для них выполнено, что $|⃗x|2 = a2+ c2$ , $|⃗y|2 = b24 + 2b24-=b2$ , $√- ⃗x⋅⃗y = 12(ab+bc 3)$

Тогда условие задачи перепишется, как

( ||||⃗x|2+ |⃗y|2 = 1 {2⃗x⋅⃗y → max |||( a,b,c> 0

Как известно $⃗x⋅⃗y = |⃗x|⋅|⃗y|⋅cos(⃗x;⃗y)≤|⃗x|⋅|⃗y|$ , где $cos(⃗x;⃗y)$ - угол между векторами.

Далее $|⃗x|+|⃗y|2 1 |⃗x||⃗y|≤ ( 2 )= 4$ по неравенству о средних.

В итоге, получается, что $√ - 1 1 ab+ bc 3= 2⃗x⋅⃗y ≤ 2|⃗x|⋅|⃗y|≤24 = 2$ . При этом равенство достигается, когда векторы $⃗x,⃗y$ равны. Тогда $-b √3b a =2,c= 2$ и $2 2 1 b = |⃗y| = 2$ . То есть подойдут, например, $√2 √2 √6- a= 4 ,b= 2 ,c = 4$ .

Второе решение.

Попробуем получить оценку следующего вида: $√- 2 2 2 ab+bc 3≤ r(a +b + c).$ Заметим, что если выражение $2 2 ka − ab+ mb$ — полный квадрат, то мы можем оценить $ab$ сверху выражением $2 2 ka + mb .$ Аналогично можно оценить $√- 3bc$ выражением $2 2 nb +tc.$ Попробуем подобрать числа $k,m,n$ и $t$ таким образом, чтобы получить желаемую оценку.

Во-первых, чтобы $ka2− ab+mb2$ сворачивалось в $√- √ -- ( ka − mb)2,$ необходимо, чтобы $1 km= 4.$ Аналогично во втором неравенстве необходимо, чтобы $nt= 34.$

Во-вторых, нужно потребовать, чтобы $k= t=n +m,$ тогда мы получим желаемую оценку исходного выражения. Решая систему из полученных уравнений, получаем, что $k =t= 1,m= 14,n = 34.$ Таким образом, неравенства примут вид $2 √- 2 ab≤ a2+ b4 , 3bc≤ 3b4-+c2,$ то есть $√ - ab+ 3bc≤ a2+ b2+ c2 = 1.$ Равенство в последнем неравенстве будет лишь тогда, когда оно будет в двух вспомогательных неравенствах, которые равносильны $0≤ (a− b2)2$ и $√ - 0≤ (23b− c)2.$ Следовательно, равенство будет при $√- a= b2,c= -32b.$ Подставляя это в равенство из условия, получим $√- √- √- a= -24 ,b=-22 ,c=-64 .$

Ответ:

$1$

Ошибка.
Попробуйте повторить позже

Задача 9#71015

Найдите максимальное значение величины $x2+ y2 +z2,$ если известно, что

2 2 2 x +y + z = 3x+8y+ z.

Источники: Надежда энергетики-2023, 11.2 (см. www.energy-hope.ru)

Подсказки к задаче

Подсказка 1

На что намекает сумма квадратов?)

Подсказка 2

На квадрат длины вектора! Введем декартову систему координат. С левой части мы разобрались - это квадрат длины вектора (x, y, z). А чем является правая часть?)

Подсказка 3

Правая часть - это скалярное произведение векторов a = (x, y, z) и c = (3, 8, 1). Теперь правую часть можно оценить сверху с помощью длин сомножителей, осталось лишь сделать вывод) Помним, что вектор c - фиксированный!

Показать ответ и решение

Введем декартову систему координат и рассмотрим произвольный вектор $a$ с координатами $(x,y,z)$ и фиксированный вектор $c$ с координатами $(3,8,1)$ . Тогда левая часть условия представляет собой квадрат длины вектора $a,$ а правая — скалярное произведение векторов $a$ и $c :$

2 |a|= (a,c)

Оценивая скалярное произведение через длины сомножителей, получаем

2 |a| ≤|a|⋅|c|⇔ |a|≤ |c|

Как известно, равенство возможно, а достигается при векторах, лежащих на одной прямой. Поэтому максимальное значение будет достигаться, например, при $a = c.$

Подставляя значения, получаем $32+ 82 +11 = 74.$

Ответ: 74

Ошибка.
Попробуйте повторить позже

Задача 10#69930

Найти решение уравнения в натуральных числах $x$ и $y :$

∘ 2---2------------ ∘-2---2------------ x +y − 2x− 6y +10+ x + y − 18x − 6y+ 90− 10 =0

Источники: САММАТ-2023, 11.7 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

У нас в задаче присутствует равенство √a+√b=c. Хочется возвести в квадрат, но, если возводить прямо так, у нас получится произведение корней √ab. Поэтому разумно было бы перенести один корень направо и возвести в квадрат...

Подсказка 2

После возведения в квадрат и приведения подобных, можно оставить корень в одной стороне, а все остальное отправить в другую и опять возвести в квадрат. Можно ли как-то после этого удачно сгруппировать слагаемые?

Подсказка 3

Получается следующее: (x-5)²/5²+(y-3)²/3²=1. Но тогда |x-5|≤5 и |y-3|≤3 ⇔ 0≤x≤10 и 0≤y≤6. Осталось перебрать x и y и найти искомые решения!

Показать ответ и решение

Если выделить полные квадраты под корнями, то уравнение можно записать в виде

∘-------------- ∘-------------- (x− 1)2+ (y− 3)2+ (x− 9)2+ (y− 3)2 = 10

Этому уравнению удовлетворяют такие пары точек $(x,y)$ , сумма расстояний от которых до точек $(1,3)$ и $(9,3)$ равна $10.$

Множеством точек плоскости, обладающих таким свойством, является эллипс. По его фокусам легко восстановить канонический вид уравнения (центр эллипса находится в середине между фокусами, координаты считаются как полусумма, соответственно считаются и длины больших полуосей):

(x− 5)2 (y− 3)2 --52--+ --32-- =1

Перебором $5≤ x≤ 10$ и $3≤y ≤6$ можно найти решения $(5,6)$ и $(10,3)$ , а им из симметрии соответствуют пары $(5,0)$ и $(0,3)$ . В ответ же записываем только пары, у которых обе компоненты натуральные.

Ответ:

$(10,3),(5,6)$

Ошибка.
Попробуйте повторить позже

Задача 11#69864

Митя собирается согнуть квадратный лист бумаги $ABCD.$ Митя называет сгиб красивым, если сторона $AB$ пересекает сторону $CD$ и четыре получившихся прямоугольных треугольника равны. Перед этим Ваня выбирает на листе случайную точку $F.$ Найдите вероятность того, что Митя сможет сделать красивый сгиб, проходящий через точку $F.$

Подсказки к задаче

Подсказка 1

Для начала нужно определить здесь, что является всеми возможными исходами, а что является положительными. Очевидно, что все возможные случаи расположения точки F - это вся плоскость квадрата, значит, нам нужно найти как именно мы можем проводить линию сгиба, так как все возможные линии сгиба в объединении образуют как раз все положительные исходы расположения точки F.

Подсказка 2

Давайте проведем линию сгиба, которая точно является красивой. Что мы можем сказать про треугольнике, которые образованы линией сгиба, диагональю и сторонами квадрата?

Подсказка 3

Такие треугольники будут равны по стороне и двум углам (докажите это, воспользовавшись равенством прямоугольных треугольников из условия «красоты» линии сгиба). Из равенства следует, что все красивые линии сгиба проходят через центр квадрата. Подумайте, как можно изобразить все красивые линии сгиба и какую часть от общей площади квадрата они займут.

Показать ответ и решение

$PIC$

Развернём красивый сгиб (правый рисунок). Пусть диагональ $BD$ и линия сгиба $ST$ пересекаются в точке $O.$ Треугольники $BSO$ и $DT O$ равны по стороне и двум углам. Значит, $BO = OD,$ и поэтому $O$ — центр квадрата. Таким образом, линия сгиба $ST$ проходит через центр квадрата. Очевидно, обратное также верно — если линия сгиба проходит через центр квадрата, то сгиб будет красивым.

Точка $S$ может занять любое положение между $B$ и $C,$ а точка $T$ при этом расположена между $D$ и $A.$ Значит, чтобы через точку $F$ можно было сделать красивый сгиб, нужно, чтобы точка $F$ принадлежала треугольнику $BOC$ или треугольнику $AOD.$

Площадь фигуры, ограниченной этими треугольниками, равна половине площади квадрата.

Ответ:

$0,5$

Интенсивы

Глубокий разбор тем, требующих дополнительного внимания

Ошибка.
Попробуйте повторить позже

Задача 12#69862

Для тестирования новой программы компьютер выбирает случайное действительное число $A$ из отрезка $[1,2]$ и заставляет программу решать уравнение $3x+ A =0.$ Найдите вероятность того, что корень этого уравнения меньше чем $− 0,4.$

Подсказки к задаче

Подсказка 1

Вероятность это отношение удачных исходов ко всем возможным. Все возможные случаи это [1; 2], значит, нам осталось найти все А, подходящие под условие, что x < -0.4

Подсказка 2

Если подставить в уравнение x < -0.4, то мы получим необходимые A. Пересечение полученного неравенства с отрезком [1; 2] и будет всеми положительными исходами.

Показать ответ и решение

Нас просят найти вероятность того, что

A- A- − 3 < −0,4 ⇐⇒ 3 > 0,4 ⇐⇒ A > 1,2

Эта вероятность равна $2−1,2 -2−1 =0,8$ (делим длину подходящей части отрезка $[1;2]$ на его длину).

Замечание. Не важно, включаем мы точку $1,2$ или нет, вероятность от этого не меняется. Длина полуинтервала $(1,2;2]$ равна длине отрезка $[1,2;2].$ Взрывает мозг? Подумайте, какова вероятность, что компьютером выбрано число $A = 1,2.$

Ответ:

$0,8$

Ошибка.
Попробуйте повторить позже

Задача 13#69860

Во время автогонок на пункте пит-стоп производят смену шин. Известно, что автомобиль $A$ может приехать на пит-стоп в период с $9 :30$ до $10 :30,$ и длительность смены шин составляет $10$ мин, а автомобиль $B$ — в период с $9:30$ до $10:20$ и пробудет на пункте 20 мин. Какова вероятность того, что автомобили $A$ и $B$ встретятся на пункте пит-стоп?

Подсказки к задаче

Подсказка 1

Давайте для начала введем координатные оси, отвечающие за время приезда каждой машины. Как удобнее всего это написать?

Подсказка 2

Будем считать, что одно деление по x или по y - это 10 минут, а начало координат по факту время 9:30. Тогда как будет выглядеть наше условие?

Подсказка 3

Время приезда для двух машин - это точка в прямоугольнике размером 5 на 6, а чтобы выполнялось условие, надо чтобы эта точка удовлетворяла двум условиям: y <= x+10 и x <= y+20. Осталось просто найти площади обеих фигур и посчитать их отношение)

Показать ответ и решение

Когда речь идёт о времени, удобно применить геометрический подход к вероятностям. Введём прямоугольник $ABCD$ размерами $5×6$ ( $50×60$ ), при этом в одном делении будет $10$ минут. Далее условия задаются с помощью $y ≤ x+ 10,x ≤y +20$ — то есть второй автомобиль приезжает не более, чем через $10$ минут после первого, а первый не более, чем через $20$ после второго.

$PIC$

А найти нужно площадь фигуры между прямыми и внутри нашего прямоугольника

p= SAKLCMN--= 30-− 16-=-7 SABCD 30 15

Ответ:

$-7 15$

Ошибка.
Попробуйте повторить позже

Задача 14#69821

Пешеход, велосипедист и мотоциклист едут по шоссе в одну сторону с постоянными скоростями. В тот момент, когда мотоциклист догнал велосипедиста, пешеход обгонял их на 4 км. В тот момент, когда велосипедист догнал пешехода, мотоциклист обгонял их на 6 км. На сколько километров велосипедист отставал от мотоциклиста в тот момент, когда мотоциклист обгонял пешехода?

Источники: САММАТ-2023, 11.2 (см. sammat.samgtu.ru)

Подсказки к задаче

Подсказка 1

Итак, перед нами задачка на одновременное движение нескольких объектов. Можно было бы записать систему уравнений и пытаться как-то решать с её помощью, но есть еще один очень интересный способ. Давайте построим график S(t), да-да, именно так, как мы делаем это в физике.

Подсказка 2

Пускай график перемещения мотоциклиста пересекается с графиком велосипедиста в точке A, а график пешехода - в точке D. А графики перемещения велосипедиста и пешехода пересекаются в точке E. Пускай точка B - точка на графике пешехода в момент, когда мотоциклист встретился с велосипедистом, C - точка на графике велосипедиста в момент, когда мотоциклист встретился с пешеходом, а F - точка на графике мотоциклиста в момент, когда велосипедист встретился с пешеходом. Что мы можем сказать по данному рисунку про пары треугольников △ABE, △CDE и △ABD, △FDE?

Подсказка 3

Абсолютно верно, △ABE подобен △CDE, а △ABD подобен △FDE. Так же из условия нам известны расстояния AB и EF. Теперь воспользуйтесь подобиями и длинами расстояний, чтобы найти CD.

Показать ответ и решение

$PIC$

Построим схематично график движения.

По условию задачи $AB = 4$ км, $EF = 6$ км, а требуется найти $CD.$ Очевидно, что треугольники $ABD$ и $EDF$ подобны и их коэффициент подобия $k = 4= 2. 6 3$ С другой стороны, треугольники $ACD$ и $AEF$ также подобны и их коэффициент подобия равен

--2x--= 2 2x+ 3x 5

Значит, $CD =6 ⋅ 2= 2,4. 5$

Ответ: 2,4

Ошибка.
Попробуйте повторить позже

Задача 15#64356

Пункты $A$ , $B$ , $C$ расположены последовательно, причём расстояние $AB$ равно 3 км, а расстояние $BC$ равно 4 км. Из пункта $A$ выехал велосипедист и поехал в пункт $C$ . Одновременно с ним из пункта $B$ вышел пешеход и направился в пункт $A$ . Известно, что пешеход и велосипедист пришли в пункты $A$ и $C$ одновременно. Найдите, на каком расстоянии от пункта $A$ они встретились.

Подсказки к задаче

Подсказка 1

Нарисуйте графики движения в осях “время – расстояние”. Не забывайте, что стартовые и конечные точки у пешехода и велосипедиста разные. Длину какого отрезка мы тогда хотим найти?

Подсказка 2

Конечно проекции отрезка велосипедиста на ось расстояния! При этом мы знаем длину проекции всего отрезка велосипедиста. А что мы точно можем сказать про проекции отрезков с некоторой прямой на другую прямую?

Подсказка 3

Проекции соотносятся так же, как и длины самих отрезков! Этот факт нетрудно доказывается с применением обобщенной теоремы Фалеса. Остается только найти соотношение из планиметрических соображений и вычислить искомую длину.

Показать ответ и решение

Нарисуем графики движения.

$PIC$

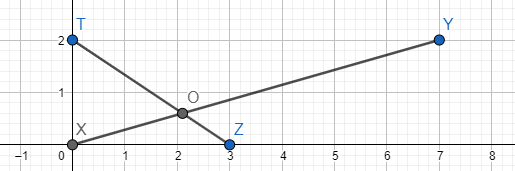
Тогда по условию $XZ =3$ и $TY = 7.$ Из признака подобия $OX-= XZ= 3. OY TY 7$ Отсюда доля пути из $A$ в $C$ , которую проехал велосипедист до его встречи с пешеходом равна $OX- 3- XY = 10$ . Значит, от точки встречи до пункта $A$ расстояние $-3 10 ⋅AC = 2,1.$

Ответ:

2100 метров

Ошибка.
Попробуйте повторить позже

Задача 16#64355

Из пункта А в пункт В в 7:00 вышел пешеход, а через некоторое время из В в А выехал всадник. Пешеход пришел в В через 10 часов после выезда оттуда всадника. Всадник приехал в А в 12:00 того же дня. Скорости пешехода и всадника постоянны. Какую долю пути из А в В прошел пешеход до его встречи со всадником?

Подсказки к задаче

Подсказка 1

Нарисуйте графики движения в осях “время – расстояние”. Не забывайте, что стартовые точки у пешехода и всадника разные как по времени, так и по “расстоянию” относительно кого-то из них. Соотношение длин каких отрезков мы хотим найти?

Подсказка 2

Нам нужны проекции отрезков пешехода “до встречи” и “всего пути” на ось расстояния. Что мы точно можем сказать про проекции отрезков с некоторой прямой на другую прямую?

Подсказка 3

Показать ответ и решение

Нарисуем графики движения.

$PIC$

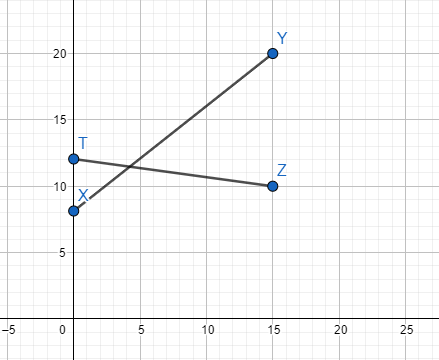
По условию $YZ = 10$ , а $XT =12− 7= 5$ . Пусть $XY$ и $TZ$ пересекаются в точке $O.$

Из подобия $OX- TX- 5- 1 OY = YZ = 10 = 2.$ Отсюда доля пути из $A$ в $B$ , которую прошел пешеход до его встречи со всадником равна $OX- 1 XY =3$ .

Ответ:

$1 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 17#63951

Найдите наименьшее значение функции

∘ --2------- ∘--2------- f(x)= 2x + 2x +13+ 2x + 8x+ 26.

Источники: Миссия выполнима - 2023, 11.7 (см. mission.fa.ru)

Подсказки к задаче

Подсказка 1

Конечно, эту задачу можно решить с помощью производной… Но давайте попробуем найти более красивое решение! Давайте подумаем, нам нужно найти минимальное значение суммы двух корней, а что мы знаем про корни и как тогда можно представить их?

Подсказка 2

Да, корни всегда положительны! Поэтому мы можем представить их как отрезок или же вектор на плоскости! То есть, корень – это длина нашего вектора! В таком случае, каких векторы можно взять(с какими координатами), чтобы длина первого равнялась первому корню, а длина второго равнялась второму корню?

Подсказка 3

Так, длина вектора – это корень из суммы квадратов его координат! Первое подкоренное выражение обращается в ноль при x=-3 и при x=2, а второе при x=1 и при x=-5. Поэтому первый вектор равен (x+3;2-x), а второй вектор: (1-x)(x+5). Что можно сказать про сумму этих векторов?

Подсказа 4

Да, сумма этих векторов равна другому вектору: (4; 7). А длина этого вектора равна √65. Но заметим, что сумма длин исходных векторов не меньше чем длина получившегося вектора! Осталось показать, что минимальное значение достигается и задача решена!

Показать ответ и решение

Рассмотрим векторы

⃗ ⃗ ⃗a= (x +3;2− x),b= (1− x;x+ 5) и⃗s= ⃗a+ b= (4;7)

Так как

∘ -2-------- ⃗ ∘ --2------- |⃗a|= 2x + 2x+ 13, |b|= 2x + 8x +26

то

f(x)= |⃗a|+|⃗b|≥|⃗a+⃗b|= |⃗s|= √65

Равенство $|⃗a|+|⃗b|= |⃗a +⃗b|$ выполняется, когда эти векторы сонаправлены; соответствующие значения $x$ является корнем уравнения $x1+−3x = 2−xx+5$ и равно $− 1311-$ .

Ответ:

$√65$

Ошибка.
Попробуйте повторить позже

Задача 18#76639

Клиенты интернет магазина «Али-экспресс» проживают в семи домах, расположенных в вершинах выпуклого семиугольника. От жителей первого дома поступил один заказ, от второго дома – два заказа, и т.д. от жителей шестого – шесть заказов. А вот жители последнего седьмого дома сделали $21$ заказ. Менеджер магазина задумался о том в какое место следует доставить все заказы, чтобы суммарное расстояние, преодолеваемое всеми клиентами для получения товара, было минимально возможным. Помогите ему в решении этой задачи и обоснуйте результат.

Источники: Росатом-2022, 11.1 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Пусть точка О - выбранная нами. Обозначим расстояние от О до i-того дома за d_i. Какую сумму мы хотим минимизировать? Что интересного можно заметить среди коэффициентов?

Показать ответ и решение

Пусть $O$ – произвольная точка привоза товара, $d ,d,,...,d 1 2 7$ – расстояния от точки привоза до домов; Суммарное расстояние:

∑ =1 ⋅d1+ 2d2+3d3+ 4d4 +5d5+ 6d6+ 21d7 =

= (d1+ d7)+ 2(d2+ d7)+4(d4+d7)+ 5(d5+ d7)+ 6(d6+ d7)

$PIC$

Из неравенства треугольника:

d1+d7 ≥ A7A1, d2+ d7 ≥ A7A2, d3+d7 ≥A7A3, d4+ d7 ≥ A7A4,

d5+ d7 ≥ A7A5, d6+d7 ≥ A7A6 (1)

Равенство достигается только в случае, когда треугольники вырождаются в отрезки.

∑ ≥A7A1 +2 ⋅A7A2 +3 ⋅A7A3 +4 ⋅A7A4 +5 ⋅A7A5 +6⋅A7A6 (2)

Правая часть неравенства $(2)$ не зависит от положения точки $O,$ поэтому

min∑ ≥A7A1 +2⋅A7A2 +3⋅A7A3 +4⋅A7A4 +5⋅A7A5+ 6⋅A7A6

Минимум достигается, когда точка $O$ совпадает с точкой $A7,$ поскольку в ней все неравенства $(1)$ превращаются в равенство.

Ответ: товары следует доставить в седьмой дом

Ошибка.
Попробуйте повторить позже

Задача 19#76628

Петя пришел на остановку автобуса, едущего до школы с остановками равноотстоящими друг от друга, и, не увидев автобуса на дороге, решил пробежаться и сесть в автобус на следующих остановках по пути в школу. Бежал Петя так, что в любой момент времени мог заметить появление автобуса на дороге за своей спиной. Увидев автобус, Петя может повернуть назад или сохранить направление движения. Известно, что скорость движения автобуса в 4 раза превосходит скорость бега Пети, а увидеть автобус он может на расстоянии не более 1 км. Найти наибольшее значение расстояния между остановками, при котором независимо от того повернет Петя назад при обнаружении автобуса или нет, он сможет сесть в автобус на остановке. (время нахождения автобуса на остановке не учитывать)

Источники: Росатом-2022, 11.1 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Это задача на движение и скорости. Значит, здесь можно ввести достаточное количество переменных и тождественными преобразованиями/оценками получить всё, что нам нужно. Если расстояние до остановки, которая сзади Пети - x, а расстояние между остановками равно а (в момент того, как Петя увидел автобус), то нам надо понять, для каких а как надо поступать Пете, чтобы точно сесть на автобус.

Подсказка 2

Это зависит от неравенства со скоростями. Пете удобно бежать к задней остановке, если x/v ≤ (1 - x) / (4v), где v - скорости Пети. То есть когда расстояние до остановки сзади не больше 1/5. Попробуйте написать такое же неравенство, когда ему надо бежать к передней остановке и понять, как оба этих неравенства ограничивают а.

Подсказка 3

(a - x)/v ≤ (1 - x - a)/(4v). Остаётся только написать пример, когда это достигается, но это очевидно делается, если понять, когда в каждом нашем неравенстве достигается равенство.

Показать ответ и решение

$PIC$

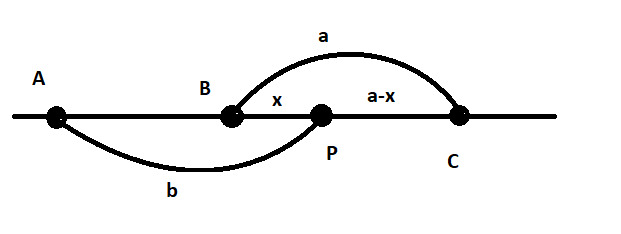
Пусть $A$ — положение автобуса на дороге в момент, когда его увидел Петя, $P$ — положение Пети на дороге в момент, когда он увидел автобус, $B$ — положение последней остановки, которую миновал Петя к моменту, когда он увидел автобус, $C$ — положение следующей за $B$ остановки, $a$ — расстояние между остановками, $X$ — расстояние между точками $B$ и $P$ , $v$ — скорость бега Пети.

Рассмотрим несколько случаев

Случай 1. Увидев автобус, Петя повернул назад. Петя окажется на остановке $B$ не позднее автобуса и сможет на него пересесть, если

x≤ 1−-x⇒ x ≤ 1 v 4v 5

Случай 2. Увидев автобус, Петя не изменил направления движения. Петя окажется на остановке $C$ не позднее автобуса и сможет на него пересесть, если

a−-x 1− x-+a 1 v ≤ 4v ⇒ a− x≤ 3

Наибольшее допустимое значение $a$ соответствует пересечению прямых $1 x= 5$ и $1 a= x+ 3.$ В итоге находим $-8 amax = 15.$

Ответ:

$-8 15$

Ошибка.
Попробуйте повторить позже

Задача 20#74915

Олег и Оливер гоняют на велосипедах с одинаковыми угловыми скоростями: Оливер — по круговой траектории $𝒜,$ а Олег — по круговой траектории $𝒯$ в два раза меньшего радиуса, причем они стартуют с двух ближайших точек окружностей и круг Олега лежит внутри круга Оливера. По окружности $𝒯$ также движутся два помощника, поддерживающих экран (т.е. хорду с концами в точках, в которых расположены помощники) так, что расстояние от каждого из них до Олега всегда такое же, как и расстояние от Олега до Оливера. Докажите, что на протяжении всей гонки экран касается некоторой фиксированной окружности.

Источники: Иннополис-2022 (см. dovuz.innopolis.university)

Подсказки к задаче

Подсказка 1

Обозначим за O,V,X и Y Олега, Оливера и двух помощников соответственно. Если нарисовать рисунок, то от нас явно спрятали какую-то известную и хорошую "картинку", посмотрите на равные отрезки, которые нам даны и на окружность 𝒯.

Подсказка 2

Верно, как будто нам показывают лишь часть картинки леммы о трезубце! Попробуйте восстановить точку, которую от нас спрятали и подумать, как эта точка поможет нам в задаче.

Подсказка 3

Давайте ещё заметим, что у нас получилась как бы "картинка в картинке", возможно, тут поможет гомотетия, попробуйте посмотреть на центр положительной гомотетии окружностей 𝒯 и 𝒜.

Подсказка 4

Да это же центр нашей искомой окружности, ещё не совсем, но можно попробовать это доказать! Мы уже знаем, что она точно касается экрана и её центр не меняется, остаётся показать, что её радиус тоже фиксирован, а какой факт связывает точку, окружность и радиус?

Подсказка 5

Можно использовать степень точки S относительно 𝒯, останется только "перекинуть" равные отрезки так, чтобы остались только фиксированные величины (из исходной "картинки") и радиус окружности с центром в S.

Показать доказательство

Обозначим за $O,V,X$ и $Y$ Олега, Оливера и двух помощников соответственно, за $S$ — центр положительной гомотетии окружностей $𝒯$ и $𝒜.$ Из условия следует, что прямая $V O$ всегда проходит через $S,$ причем, так как радиусы окружностей отличаются в два раза, отрезок $SV$ делится точкой $O$ пополам. Отметим точку $R ⁄= O$ — пересечение луча $OS$ с $𝒯.$ Поскольку равные хорды стягивают равные меньшие дуги, точка $O$ — середина дуги $XOY,$ то есть прямая $RO$ содержит внутреннюю биссектрису треугольника $XRY,$ а еще $OS = OV =OX =OY.$ По лемме о трезубце это означает, что точка $S$ является центром вписанной окружности треугольника $XRY$ $($ обозначим эту окружность за $ω).$

$PIC$

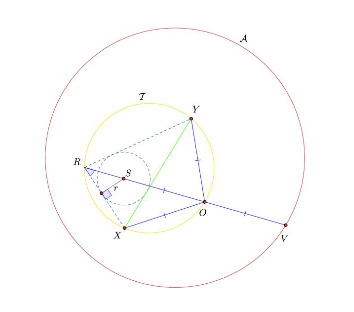
Покажем, что $ω$ является искомой окружностью. Она касается отрезка $XY$ в силу построения, поэтому достаточно проверить, что она не зависит от времени. Как показано выше, центр $ω$ — это $S,$ обозначим ее радиус за $r$ . Также обозначим за $d$ расстояние между центрами $ω$ и $𝒯,$ а за $R$ — постоянный радиус $𝒯.$

Посчитаем степень точки $S$ относительно $𝒯$ двумя способами:

d2− r2 = −RO ⋅SO = −RO ⋅OX =− RO⋅2R sin∠XRO = −2Rr

Величины $d$ и $R$ не зависят от времени, поэтому $r$ также от него не зависит, следовательно, окружность $ω$ имеет постоянный центр и радиус, что и требовалось доказать.

Предыдущий раздел

Следующий раздел