Ошибка.
Попробуйте повторить позже
Дан треугольник с острым углом
такой, что
На сторонах
и
вне треугольника построены квадраты
и
с центрами
и
Оказалось, что точки
и
лежат на одной окружности
с центром
Доказать, что
точка
пересечения прямых
и
лежит на окружности
Источники:
Подсказка 1
Если после того, как вы нарисовали рисунок, вам показалось, что DF- диаметр нашей окружности, то вы на верном пути! Попробуйте для начала понять, как связана точка I, центр описанной окружности треугольника △ABC, с точкой O, а потом придумаем что-нибудь с DF.
Подсказка 2
Мы знаем, что I- точка пересечения серперов к AB и AC, а O- точка пересечения серперов к DE и FG. Но тогда I=O. Мы хотим, чтобы DF оказался диаметром. Давайте докажем, что E, A и F лежат на одной прямой...
Подсказка 3
Если это не так, то EA пересекает нашу окружность в точке T, отличной от F. Продлим прямые FC и DB до пересечения в точке Z. Посмотрите на точку O и подумайте, каким является четырехугольник DATZ...
Подсказка 4
Т.к. O является одновременно серединой AZ и DT ⇒ DATZ- параллелограмм ⇒ TZ=AD и ∠ATZ=45°. Что мы можем сказать про четырехугольник AFTZ?
Подсказка 5
Он вписан, ведь ∠AFZ=∠ATZ=45°. Отрезки OF и OT равны как радиусы. Тогда O лежит на серпере к AZ и на серпере к FT. Что это нам дает?
Подсказка 6
Если эти серперы не совпадают, то O- центр описанной окружности AFTZ, что противоречит тому, что ∠ATZ=45°. Тогда они совпадают ⇒ AFTZ- равнобокая трапеция. На какое противоречие с условием это нас наводит?
Подсказка 7
Если это так, то AD=ZT=AF ⇒ AB=AC, что не так. Ура!! Мы доказали, что наше предположение неверно, а это значит, что E, A и F лежат на одной прямой. Аналогично G, A и D лежат на одной прямой. Тогда для полного счастья нам осталось лишь доказать, что ∠EMG=∠EDG=45°...
Подсказка 8
Посмотрим на четырехугольник KALM: ∠AKM=∠ALM=90°. Тогда ∠EMG=180°-∠KAL. Докажите, что ∠KAL=135° и наслаждайтесь победой!
![]()
Заметим, что — точка пересечения сер. перп. к
,
, но
и
— точка пересечения сер. перп. к
и
— центр описанной окружности
.
Докажем, что ,
и
лежат на одной прямой.
Пусть это не так, тогда пересекает нашу окружность в точке
, отличной от
. Продлим прямые
и
до пересечения в
точке
.
![]()
Т.к. является одновременно серединой
(
и
с коэффициентом 2) и
— диаметр)
— параллелограмм, тогда
и
—
вписанный. Отрезки
и
равны как радиусы. Тогда
лежит на сер. перп. к
и на сер. перп. к
.
Если эти сер. перп. не совпадают, то — центр описанной окружности
, что противоречит тому, что
. Тогда они
совпадают
— равнобокая трапеция.
Если это так, то , что не так. Значит, наше предположение неверно, и
,
и
лежат на одной
прямой. Аналогично
,
и
лежат на одной прямой.
![]()
Рассмотрим четырехугольник :
— вписанный
, но
и
— вписанный
лежит на окружности
.
Ошибка.
Попробуйте повторить позже
Длины сторон треугольника
периметр которого равен 6, в указанном порядке являются последовательными членами
некоторой арифметической прогрессии. Найдите ее разность, если угол
в два раза больше угла
Источники:
Подсказка 1
Представьте стороны треугольника в виде членов арифметической прогрессии. Попробуйте сделать это именно таким образом, чтобы в дальнейшем можно было удобно воспользоваться тем, что мы знаем периметр.
Подсказка 2
Пусть AB = a - d, AC = a, BC = a + d, тогда, посчитав периметр, мы находим, что a = 2. Обратите внимание на углы нашего треугольника. Какое дополнительно построение хочется сделать в данной конструкции?
Подсказка 3
Когда у нас один угол треугольника в два раза больше второго, очень удобным построением является биссектриса, проведенная из угла, который в два раза больше. Ей мы разбиваем треугольник на равнобедренный и подобный основному.
Подсказка 4
Кроме подобия мы так же можем записать свойство биссектрисы. Теперь мы получили систему уравнений с двумя неизвестными. Осталось ее решить и подумать над тем, какие d по знаку нам подходят, а какие - нет, и почему.
Так как стороны являются последовательными членами арифметической прогрессии, то пусть При этом
заметим, что
так как напротив большего угла в треугольнике лежит большая сторона. Найдем
сложив все стороны и приравняв к
6. Получим
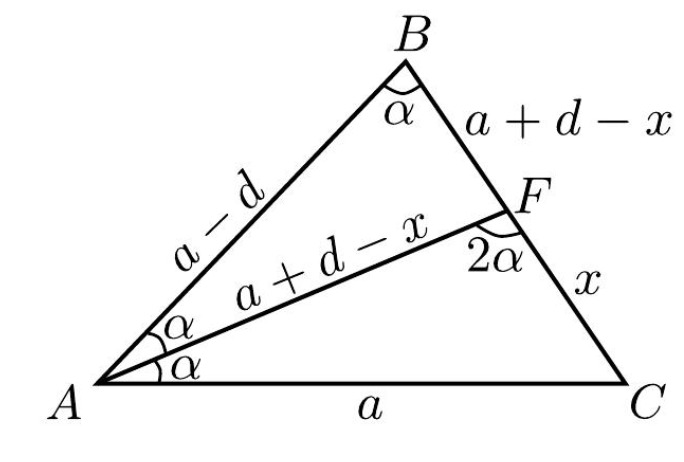
Проведем биссектрису угла и отметим равные отрезки и равные углы как на картинке.
По свойству биссектрисы
| (1) |
Так как треугольники и
подобны по двум углам
| (2) |
Подставим в
Подставим в
Ошибка.
Попробуйте повторить позже
Три окружности с радиусами попарно касаются друг друга внешним образом, а также касаются внешним образом
четвертой окружности с радиусом
Найти
Источники:
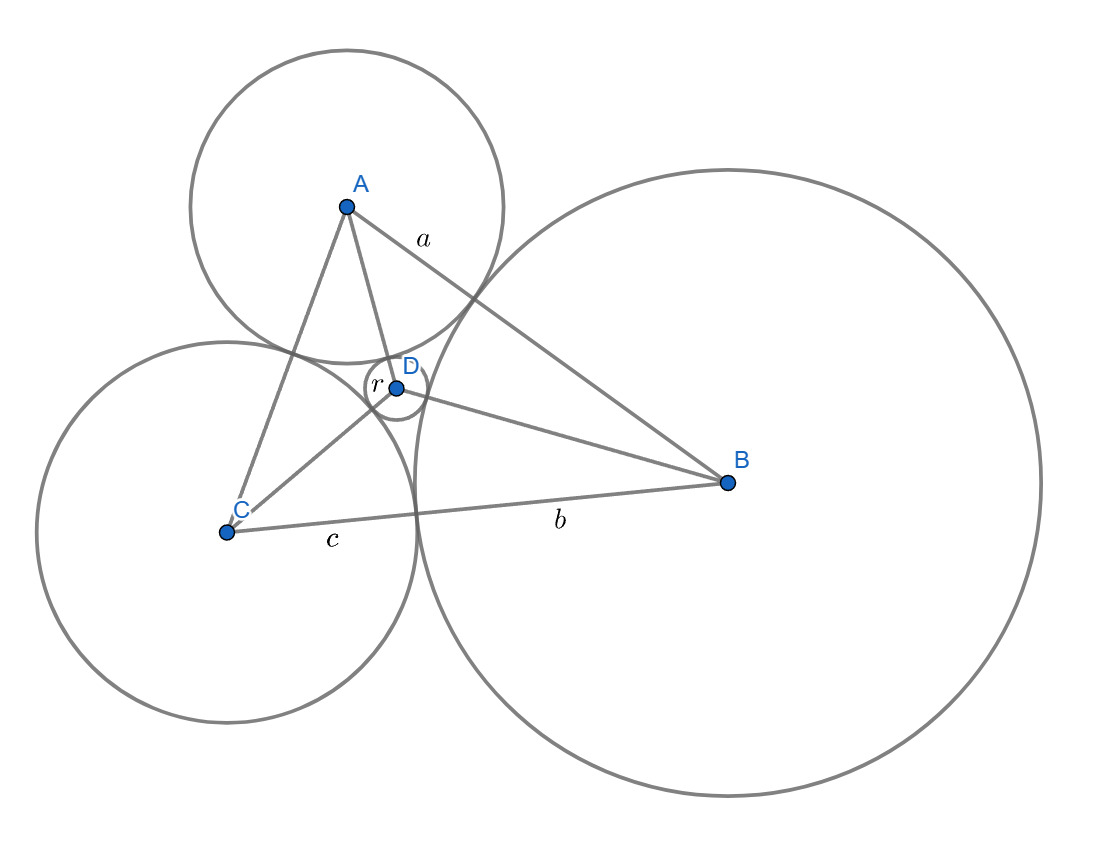
По теореме Декарта если четыре окружности касаются друг друга в шести различных точках и окружности имеют радиусы ,
то
Если пытаться отыскать радиус четвёртой окружности, касающейся трёх касающихся друг друга окружностей, уравнение лучше
записать в виде
По условию три окружности касаются четвёртой внешним образом, поэтому надо взять перед корнем знак плюс. После подстановки радиусов из условия:
Ошибка.
Попробуйте повторить позже
В треугольнике на сторонах
и
выбраны точки
и
соответственно так, что
и
Пусть отрезки
и
пересекаются в точке
Найти площадь треугольника
, если площадь четырехугольника
равна
Подсказка 1
Из условия задачи нам известна площадь четырёхугольника. А найти нужно площадь ABC. Идея попробовать выразить площадь треугольника через четырёхугольник, наверное, не очень хорошая. Но тогда какую часто встречающуюся идею здесь можно применить?
Проведем в треугольнике отрезки
и
пусть они пересекаются в точке
Пусть также площадь треугольника
равна
![]()
Треугольники и
имеют общую высоту, проведенную из вершины
поэтому их площади относятся как отношение
оснований
и
поэтому площадь треугольника равна
Треугольники и
имеют общую высоту, проведенную из вершины
поэтому их площади относятся как отношение
оснований:
поэтому площадь треугольника равна
Найдем, в каком отношении точка делит отрезок
Для этого запишем теорему Менелая для треугольника
и секущей
т.е. Тогда
Треугольники
и
имеют общую высоту, проведенную из вершины
поэтому их площади относятся как отношение оснований:
поэтому площадь треугольника равна
Но тогда площади треугольников и
равны
Таким образом, площадь четырехугольника равна разности площадей
откуда следует, что искомая площадь треугольника
равна



