Рассмотрим нарисованные окружности как плоский мультиграф (граф с кратными ребрами между вершинами): вершины – точки пересечений, ребра – дуги нарисованных окружностей, ограниченные точками пересечений. В такой интерпретации круглосторонники — это все грани этого графа, кроме «внешней» (т.е. части плоскости, лежащей вне всех окружностей).

Пусть нарисованы ровно окружностей. Согласно формуле Эйлера для плоских графов,

где — число вершин графа, — число ребер, а — – число граней (включая внешнюю).

Так как каждая пара окружностей пересекается ровно в двух своих уникальных точках, то число вершин

Так как каждая вершина – это точка пересечения ровно двух окружностей, то наш граф является регулярным степени (то есть в каждую вершину входят ровно ребра). Поскольку каждое ребро соединяет две вершины, общее число ребер

Следовательно число граней нашего плоского мультиграфа должно быть равно

Значит, число круглосторонников

Найти наименьшее такое, что — значит найти наименьшее натуральное решение неравенства

Решив, получаем, что наименьшее равно соответственно

Теперь заметим, что для любого (в том числе для можно расположить окружностей на плоскости так, что каждая пара пересекается ровно в двух своих уникальных точках. Действительно, нарисуем произвольную окружность на плоскости и выберем произвольную точку внутри нее (но не являющуюся ее центром), а потом рассмотрим окружностей где которые получаются в результате поворота окружности вокруг точки на угол (окружность совпадает с На рисунке приведен пример для

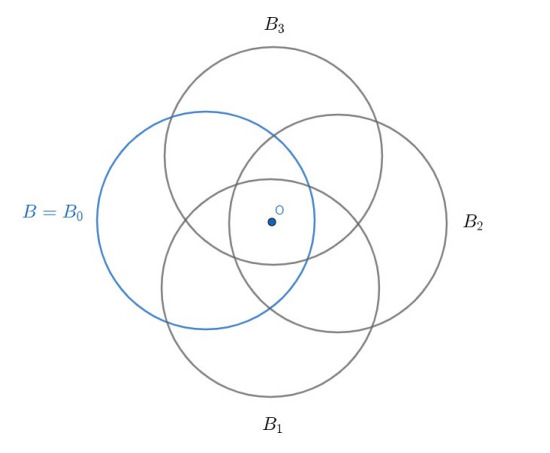
Теперь докажем, что обязательно найдется круглосторонник, ограниченный менее чем дугами. Предположим, что все круглосторонники ограничены не менее чем дугами. Тогда общее число «сторон» (дуг, ограничивающих круглосторонники) не меньше, чем Пусть — число границ внешней грани плоского мультиграфа, тогда

Это невозможно, — следовательно, неверно предположение, что все круглосторонники ограничены не менее чем дугами. Поэтому обязательно найдется круглосторонник, ограниченный менее чем дугами, что и требовалось доказать.

Для начала заметим, что в каждом квадрате должно быть по две клетки каждого цвета. Рассмотрим раскраску самой верхней строки квадрата. Предположим, что в ней есть какие-то две соседние клетки одинакового цвета. Тогда, рассмотрев квадрат содержащий эти клетки, получим, что две клетки под ними должны быть противоположного цвета. Если теперь сдвинуть этот квадрат на одну клетку вправо, получим, что в левом столбце две клетки противоположного цвета, поэтому и в правом столбце клетки тоже должны быть противоположного цвета. Сдвигая этот квадрат аналогично вправо и влево, получим, что вторая строка должна быть противоположна (по цветам) первой.

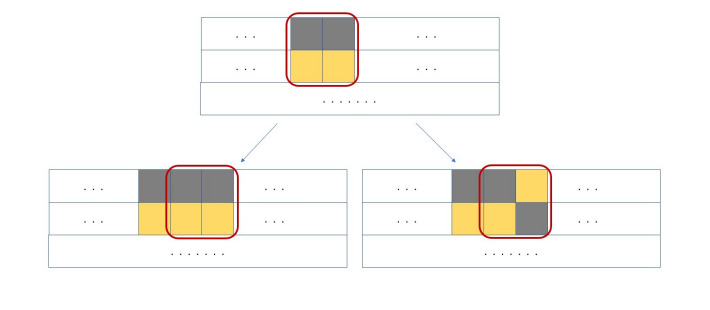
Если теперь проделать такие же рассуждения со второй и третьей строкой, получим, что третья строка должна быть противоположна второй (т.к. во второй также найдутся две рядом стоящие клетки одного цвета). Аналогично далее строки будут чередоваться, и вся таблица заполняется однозначно. Теперь поймём, при каких условиях на первую строку раскраска будет подходящей. Предположим, что в первой строке найдётся подстрока, в которой клеток одного из цветов хотя бы на больше, чем другого. Такую подстроку можно сократить до подстроки длины так, чтобы разница была ровно (т.к. при отбрасывании одной клетки разница меняется на 1). Рассмотрим квадрат размера содержащий подстроку Так как в разница между цветами равна то нечётно. Значит, в квадрате тоже разница между цветами будет равна т.к. все его строки, кроме первой, можно разбить на пары противоположных (понятно, что если в подстроке разница между цветами больше то в ней найдутся две соседние клетки одного цвета).

Таким образом, в первой строке не должно найтись подстроки, в которой клеток какого-то цвета хотя бы на больше, чем другого. Предположим, что это условие выполнено, причём каждая строка, начиная со второй, противоположна предыдущей. Тогда в любом квадрате чётного размера цветов будет поровну, а в любом квадрате нечётного размера количество клеток разных цветов будет отличаться на т.к. все строки в нём, кроме первой, разбиваются на пары, а в первой строке количество клеток разных цветов может отличаться только на

Обозначим количество подходящих раскрасок первой строки за Тогда количество подходящих раскрасок всей доски будет равно Действительно, в первой строке будет либо чередование цветов ( варианта), либо где-то встретятся две клетки одинакового цвета. Во втором случае всё остальное определяется однозначно, а в первом всё определяется раскраской первого столбца (если и в первой строке, и в первом столбце не будет двух стоящих рядом клеток одного цвета, то с помощью последовательного рассмотрения квадратов мы получим, что раскраска должна быть шахматной).

Теперь осталось найти Заметим, что трёх подряд идущих клеток одного цвета быть не может, т.к. эти три клетки уже дают подстроку с разницей Найдём в строке первый момент, когда рядом встретились две клетки одного цвета. Найдём следующий момент, когда рядом встретятся две клетки одного цвета. Если это тот же самый цвет, то в минимальной подстроке, содержащей обе эти пары, разница цветов будет равна чего быть не может. Значит, это должны быть клетки другого цвета. Таким образом, блоки из пар клеток одного цвета должны чередоваться, а ещё между этими блоками могут быть участки чётной длины из чередующихся клеток. Тогда для расположения блоков может быть два варианта: либо их первые клетки расположены на нечётных местах, либо на чётных.

В первом случае разобьём все клетки на пары подряд идущих. На месте каждой пары может быть либо блок из двух одинаковых клеток, либо пара разных клеток. По набору мест блоков и цвету самой левой клетки цвета всех остальных клеток определяются однозначно. Таким образом, вариантов в этом случае В случае, когда первые клетки блоков располагаются на чётных позициях, есть всего мест для блоков, и цвета всех клеток также определяются наборами мест блоков и цветом самой левой клетки. В этом случае вариантов При этом те варианты, где блоков вообще нет, мы посчитали дважды. Таких вариантов (когда цвета чередуются). Значит,

Получаем ответ:

Заметим, что если в куче нечетное число камней, то первый игрок гарантирует себе победу, взяв на первом ходу 1 камень: тогда каждым следующим ходом игроки будут забирать по одному камню, и последний камень заберет первый игрок. Когда чётно, тот, кто первым сделает нечетный шаг, проиграет: такой шаг был сделан из четного числа — значит, он не будет последним, а противник заберет один камень, что и обеспечит ему победу.

Если то второй игрок, очевидно, побеждает. Если то побеждает первый игрок, забирая первым ходом 1 камень. Если то побеждает второй игрок: если первый берет 1 камень, то второй возьмет последний камень, а если первый игрок первым ходом берет 2 или 3 камня, то второй игрок первым своим ходом забирает остальные камни.

Докажем по индукции, что для всех четных от до (для натурального ) побеждает первый игрок, а для — второй. База индукции разобрана выше.

Пусть для натурального Тогда первый игрок сводит игру к таковой с камнями (т.е. берет вдвое больше камней, чем взял бы в игре с камнями), где у него есть победная стратегия согласно предположению индукции, поскольку Единственный способ помешать ему — взять нечетное число камней, но, как показано выше, тот, кто первым возьмет нечетное число камней, проигрывает.

Пусть теперь для Тогда уже второй игрок применяет стратегию "половинчатой"игры, т.е. берет в 2 раза больше камней, чем взял бы в игре с камнями. Согласно предположению индукции, это обеспечит ему победу.

Пусть — искомое число помещении в зависимости от количества участников турнира. Сначала докажем индукцией по , что База для и очевидна.

Зафиксируем помещение (например, №1) и обозначим через множество шахматистов (вершин графа, каждое ребро которого соответствует определенной партии), которые играли в этом помещении белыми фигурами. Аналогично, обозначим за множество шахматистов, которые не играли в этом помещении белыми фигурами. Множества и не пересекаются — значит, хотя бы одно из них без ограничения общности будем считать, что это содержит не более элементов, остальные шахматисты (их не менее ) не играли белыми фигурами в помещении №1 — значит, им для этого хватило помещений:

Покажем, как сделать "правильное"(т.е. соответствующее условию задачи) расписание с Для этого занумеруем вершины графа (т.е. шахматистов) числами от до и ориентируем ребра графа (т.е. партии) если (шахматист играет белыми, а — черными), а помещения занумеруем числами от до Ребру поставим в соответствие номер который определяется как наибольшее такое, что в двоичной записи числа на -м месте стоит 1, а у числа — Такое существует, поскольку Кроме того, в двоичных разложениях не более цифр, откуда

Осталось проверить, что ребрам и соответствуют разные номера. Действительно, если бы им соответствовал общий номер то у числа в -м разряде двоичной записи стояла бы и цифра из-за ребра и цифра из-за ребра что невозможно.