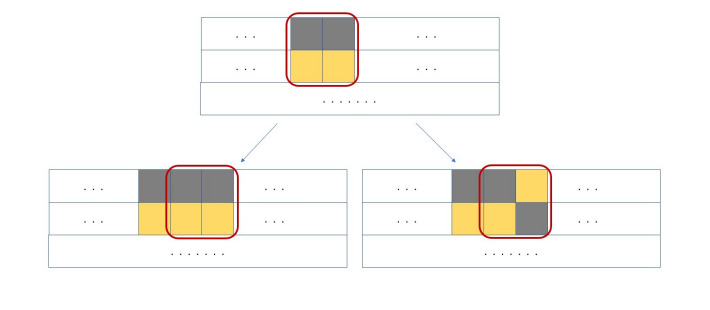
Для начала заметим, что в каждом квадрате должно быть по две клетки каждого цвета. Рассмотрим раскраску самой верхней строки квадрата. Предположим, что в ней есть какие-то две соседние клетки одинакового цвета. Тогда, рассмотрев квадрат содержащий эти клетки, получим, что две клетки под ними должны быть противоположного цвета. Если теперь сдвинуть этот квадрат на одну клетку вправо, получим, что в левом столбце две клетки противоположного цвета, поэтому и в правом столбце клетки тоже должны быть противоположного цвета. Сдвигая этот квадрат аналогично вправо и влево, получим, что вторая строка должна быть противоположна (по цветам) первой.

Если теперь проделать такие же рассуждения со второй и третьей строкой, получим, что третья строка должна быть противоположна второй (т.к. во второй также найдутся две рядом стоящие клетки одного цвета). Аналогично далее строки будут чередоваться, и вся таблица заполняется однозначно. Теперь поймём, при каких условиях на первую строку раскраска будет подходящей. Предположим, что в первой строке найдётся подстрока, в которой клеток одного из цветов хотя бы на больше, чем другого. Такую подстроку можно сократить до подстроки длины так, чтобы разница была ровно (т.к. при отбрасывании одной клетки разница меняется на 1). Рассмотрим квадрат размера содержащий подстроку Так как в разница между цветами равна то нечётно. Значит, в квадрате тоже разница между цветами будет равна т.к. все его строки, кроме первой, можно разбить на пары противоположных (понятно, что если в подстроке разница между цветами больше то в ней найдутся две соседние клетки одного цвета).

Таким образом, в первой строке не должно найтись подстроки, в которой клеток какого-то цвета хотя бы на больше, чем другого. Предположим, что это условие выполнено, причём каждая строка, начиная со второй, противоположна предыдущей. Тогда в любом квадрате чётного размера цветов будет поровну, а в любом квадрате нечётного размера количество клеток разных цветов будет отличаться на т.к. все строки в нём, кроме первой, разбиваются на пары, а в первой строке количество клеток разных цветов может отличаться только на

Обозначим количество подходящих раскрасок первой строки за Тогда количество подходящих раскрасок всей доски будет равно Действительно, в первой строке будет либо чередование цветов ( варианта), либо где-то встретятся две клетки одинакового цвета. Во втором случае всё остальное определяется однозначно, а в первом всё определяется раскраской первого столбца (если и в первой строке, и в первом столбце не будет двух стоящих рядом клеток одного цвета, то с помощью последовательного рассмотрения квадратов мы получим, что раскраска должна быть шахматной).

Теперь осталось найти Заметим, что трёх подряд идущих клеток одного цвета быть не может, т.к. эти три клетки уже дают подстроку с разницей Найдём в строке первый момент, когда рядом встретились две клетки одного цвета. Найдём следующий момент, когда рядом встретятся две клетки одного цвета. Если это тот же самый цвет, то в минимальной подстроке, содержащей обе эти пары, разница цветов будет равна чего быть не может. Значит, это должны быть клетки другого цвета. Таким образом, блоки из пар клеток одного цвета должны чередоваться, а ещё между этими блоками могут быть участки чётной длины из чередующихся клеток. Тогда для расположения блоков может быть два варианта: либо их первые клетки расположены на нечётных местах, либо на чётных.

В первом случае разобьём все клетки на пары подряд идущих. На месте каждой пары может быть либо блок из двух одинаковых клеток, либо пара разных клеток. По набору мест блоков и цвету самой левой клетки цвета всех остальных клеток определяются однозначно. Таким образом, вариантов в этом случае В случае, когда первые клетки блоков располагаются на чётных позициях, есть всего мест для блоков, и цвета всех клеток также определяются наборами мест блоков и цветом самой левой клетки. В этом случае вариантов При этом те варианты, где блоков вообще нет, мы посчитали дважды. Таких вариантов (когда цвета чередуются). Значит,

Получаем ответ: