Сначала покажем, что последовательностей не хватит.

Построим граф, вершины которого это числа от до , а рёбра между вершинами и проводятся, если в одной из последовательностей числа и были подряд идущими членами.

Так как суммарно во всех -x последовательностях каждое число будет соседом не более других чисел, степень каждой вершины в этом графе не превосходит .

Тогда выберем в графе две несмежные вершины Так как степень каждой из них не более , а всего вершин , то найдется хотя бы вершина , которая не соседствует с обеими вершинами . Тогда множество чисел не будет удовлетворять условию задачи (ни в одна последовательности нет двух или трех подряд идущих членов, которые содержатся в )

_________________________________________________________________________________________________________________________________________________________________________________

Пример на последовательностей опишем пример в терминах графа.

Разделим чисел на две равные группы: например, и .

Отдельно расставим первые чисел в последовательностей длиной , чтобы любые числа были соседями в хотя бы одной из последовательностей. (То есть на языке графов: нужно покрыть путями полный граф на вершинах). И аналогично поступим со второй группой чисел, а потом просто “склеим” последовательности. Например, если первая последовательность в первой группе это , а первая последовательность во второй - это , то склеиваем и получаем .

Опишем построение последовательностей длиной . Поместим вершины в правильный многоугольник и покроем полный граф на этом подмножестве вершин последовательностями (то есть путями проходящими по всем вершинам), идущими зигзагом через многоугольник с поворотом каждого пути на кратный угол. На картинке пример построения последовательностей, для чисел:

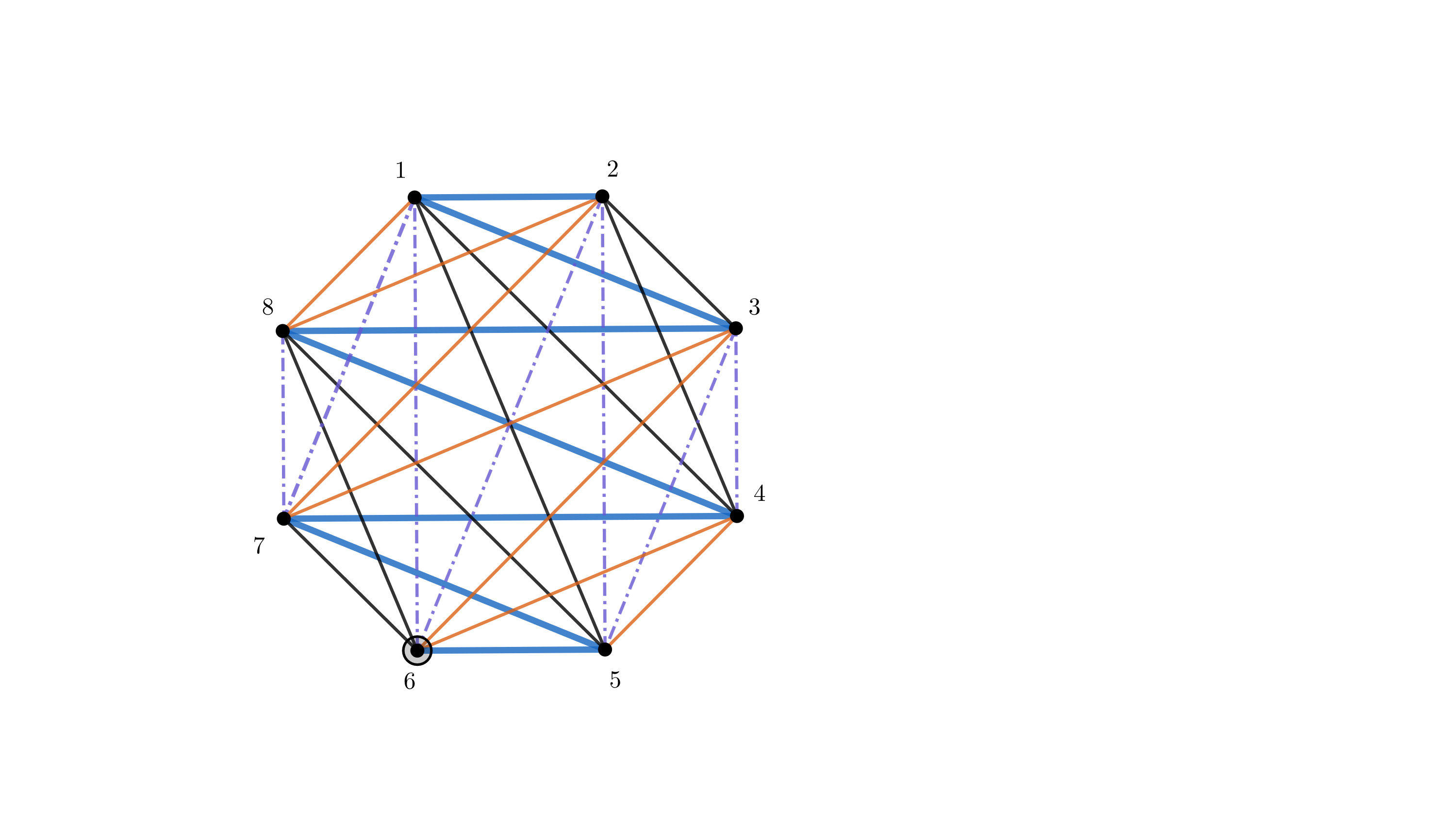
Теперь поясним, почему после "склейки"полученные последовательностей будут удовлетворять условию. Какие бы числа , мы ни взяли, либо два из них будут среди чисел от до , либо среди чисел от до . Тогда два числа из одно группы соединены ребром, то есть являются соседями в одной из последовательностей. Этого мы и добивались.

Пусть отмечены красные точки , синие точки , и зеленые точки .

Поскольку для каждой точки выполняется неравенство треугольника , то

Откуда .

Аналогично, просуммировав неравенства , получим .

Далее перебором можно установить, что найденным соотношениям и равенству удовлетворяют ровно две тройки натуральных чисел

Покажем, что оба найденных варианта могут быть реализованы на прямой. Каждую из отмеченных точек будем задавать ее координатой.

Первый вариант:

Второй вариант: .

Через где — произвольный город, обозначим число городов, соединённых беспосадочными авиалиниями с Будем рассматривать авиамаршрут, который проходит последовательно через города и все перелёты на котором централизующие. Ясно, что тогда

Равенство невозможно, поскольку имело бы своими следствиями взаимоисключающие равенства и так как еще соединена с

Допустим, что и Тогда то есть город соединён либо с либо с Но соединён с и а — с и

Наконец, предположим, что и Тогда соединён с соединён с и Получается, что город не соединён ни с ни с а тогда равенство невозможно. Итак, Приведём пример системы авиалиний, для которой все перелёты на маршруте, проходящем последовательно через города централизующие. Пусть города и () соединены, если выполнено хотя бы одно из следующих трёх условий:

Первое решение.

Первого человека в тройку возьмём любого из 18. Дальше нужно выбрать второго и третьего. Пусть между первым и вторым при подсчёте по часовой стрелке сидит человек, между вторым и третьим — между третьим и первым —

По условию должно выполняться При этом (если 3 человека выбрано, то 15 не выбраны). Если уменьшить каждую из переменных на единицу, то получаем уже уравнение в натуральных числах По методу шаров и перегородок оно имеет решений.

Итак, для каждого из 18 способов выбора первого есть 55 способов однозначно определить оставшихся двух людей. Но по условию задачи нас спрашивали количество троек без различия, кто в этой тройке первый. Поэтому нужно поделить на , ведь каждую тройку мы посчитали по три раза, когда какой-то человек являлся в ней первым.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Пронумеруем места за столом по часовой стрелке от до

Посчитаем, сколько троек мы можем создать, если один из людей сидит на первом месте.

В этом случае мы не сможем взять людей, сидящих на и местах. То есть следующего мы сможем выбрать только способами. Если следующим мы выбираем человека, сидящего на месте, то следующего можно выбрать с по место, то есть способами; если вторым выбираем человека на месте, то третьего можно выбрать способами и т.д.

В итоге, если один из выбранных людей сидит на первом месте, то существует способов подобного выбора.

Общее количество выбора троих людей указанным в условии способом равно:

Отметим, что после умножения на общее число людей, необходимо разделить на так как в каждой тройке можно начинать выбор с любого из трех людей.

Пусть число участников турника равно а число попавших в -ю группу равно . Тогда число сыгранных партий равно:

где

откуда

Если то:

тогда - противоречие;
- противоречие;
- противоречие;
- противоречие;
при и

Если то:

тогда - противоречие;
- противоречие;
- противоречие;
- противоречие;
при и

Если то:

тогда - противоречие;
- противоречие;
- противоречие;
- противоречие;
- противоречие;
- решение.
при и

Итак, наибольшее возможное число участников равно , группы участников насчитывают и человек, количество «межгрупповых» партий равно .

Пусть определяют по слову языка альфов количество в нём букв А и Л соответственно. Заметим, что все операции не меняют значения величины по модулю Действительно, порядок букв на это свойство не влияет. Остальные же операции либо просто не меняют эту разность (ЛА ФФ, ФФ ЛА), либо изменяют ровно на (АФ ЛЛ, ФЛ АА, ЛЛ АФ, АА ФЛ). Но тогда значение должно совпадать по модулю для двух рассмотренных слов. Для ЛЛАФАЛАФФАЛАФФФАЛАФФФФАЛЛ оно равно а для ЛФАЛФАЛФАЛФАЛАФЛАФЛАФЛАФЛ равняется Эти числа не равны по модулю

Если апреля все сотрудники компании сказали правду, то для сотрудника с наибольшей заработной платой второе утверждение будет ложно, что быть не может. Если же все они солгали, то первое утверждение для сотрудника с наибольшой сложной работой будет верно, то есть вновь получаем противоречие. Таким образом, существует хотя бы один солгавший и хотя бы один сказавший правду.

Возьмем сотрудника, сказавшего правду с наибольшей зарплатой из всех правдивых сотрудников. Поскольку из его второго утверждения следует, что по меньшей мере «лжецов» имеют большую зарплату, чем он. Второе утверждение солгавшего сотрудника, имеющего наименьшую зарплату среди «лжецов» ложно, таким образом, не более «лжецов» имеют большую зарплату и не более «лжецов» всего. То есть лжецов всего

Первое утверждение для «лжеца» с наиболее трудной работой среди всех «лжецов» ложно, поэтому существуют по меньшей мере правдивых сотрудников, имеющих более трудную работу.

Первое утверждение для правдивого сотрудника с наименее сложной работой среди всех правдивых сотрудников верно, поэтому существует не более правдивых сотрудников всего. То есть правдивых сотрудников ровно Окончательно получаем, что в компании работают сотрудника.

Рассмотрим случаи.

1) Код содержит комбинацию цифр . Ее можно расположить в коде тремя способами: , или . В каждом из этих возможных кодов каждую из остальных цифр можно выбрать способами. Таким образом, получается вариантов.

2) Код содержит комбинации и , причем комбинация расположена левее. Тогда оставшуюся цифру можно выбрать способами и поставить ее на одно из трех мест: перед , между и , после . То есть вариантов.

3) Код содержит комбинации и , причем комбинация расположена правее. Аналогично - вариантов. Заметим, что числа , , , мы посчитали дважды. Таким образом, чтобы открыть сейф достаточно перебрать номеров.