Приведём одну из возможных выигрышных стратегий для Пети. Он всё время будет делать ходы, параллельные одной из диагоналей доски (назовём её главной).

Первым ходом Петя закрасит все клетки главной диагонали. После этого доска разбивается на две одинаковых “лесенки” (см. рис. ). Мысленно сделаем каждую лесенку симметричной относительно вертикальной прямой, сдвинув в ней каждый горизонтальный ряд, кроме первого, на полклетки относительно предыдущего ряда (см. рис. ).

В результате сдвигов и бывшие вертикали, и бывшие диагонали, параллельные главной, стали наклонными рядами. При этом “вертикали” одной лесенки симметричны “диагоналям” другой. Это значит, что на каждый ход Васи Петя может ответить симметричным ходом в другую лесенку (два таких ответа показаны на рис. ).

Тогда после каждого Петиного хода ситуация на «сдвинутой» картинке будет оставаться симметричной, а значит, Петя всегда сможет сходит согласно описанной стратегии. Так как игра закончится (не более чем за ходов), в некоторый момент Васе будет некуда ходить, и Петя выиграет.

Пусть

По теореме Виета искомая сумма равна

Запишем условие на равенство значений трёхчленов в заданных точках (подставим вместо соответствующее значение аргумента):

Поскольку красные фишки не могут меняться местами с зелёными, их взаимный порядок всегда будет оставаться таким же, как исходный. Иначе говоря, если в любой момент убрать синие фишки, то останутся красных фишек, стоящих подряд, и зелёных, также стоящих подряд. Если требуемого удалось добиться, это означает, что мы удалили хотя бы по одной синей фишке с каждого из интервалов между соседним красными фишками и с каждого из интервалов между соседними зелёными фишками; но тогда синих фишек было бы не меньше, чем что не так. Значит, требуемое невозможно.

Поскольку при любой перестановке переменных левая часть неравенства либо не меняется, либо меняет знак, достаточно проверить неравенство для любой перестановки чисел и для которой левая часть неотрицательна. Поэтому можно считать, что Обозначим тогда Равенство из условия задачи преобразуется к виду

а требуемое неравенство — к виду

Рассмотрим правую часть равенства как квадратный трёхчлен от Поскольку он имеет корень, его дискриминант неотрицателен, то есть

откуда

Осталось показать, как из следует (при ).

По неравенству о средних для двух чисел имеем откуда Значит,

то есть Итак,

что и требовалось.

Если в некоторый момент среди чисел на карточках ровно нечётных, то среди произведений троек чисел ровно нечётных; поэтому число на очередной добавляемой карточке будет нечётным ровно тогда, когда нечётно (и тогда в эту минуту увеличится на ).

Заметим, что число нечётно, а число — чётно. Значит, в первую минуту добавится нечётное число, а дальше будут добавляться только чётные. Итак, после первой минуты среди чисел на карточках всегда будет ровно нечётных.

Рассмотрим числа на карточках после минут. Пусть — сумма всех произведений троек этих чисел, а — сумма всех произведений пар этих чисел. Число отличается от прибавлением всех произведений троек чисел, среди которых есть только что добавленное, то есть прибавлением итак, Заметим при этом, что при Значит, при число нечётно, и степень двойки, на которую делится равно степени двойки, на которую делится

Итак, после первой минуты степень двойки, на которую делится добавляемое число всегда равна степени двойки, на которую делится Значит, если бы после второй минуты на карточках не было числа, делящегося на то и впоследствии такого числа бы не появилось. Отсюда и следует требуемое.

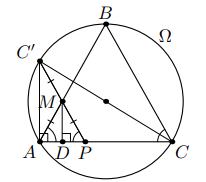
Так как диаметр имеем Поскольку получаем Значит, треугольник — равнобедренный, и поэтому его высота является и медианой. Так как и по теореме Фалеса получаем, что

Рассмотрим степени двойки, на которые делятся выписанные числа; пусть — наибольшая из них. Если хотя бы два выписанных числа делятся на то два соседних таких числа будут различаться на Значит, одно из них делится на что невозможно в силу выбора Следовательно, среди выписанных чисел ровно одно делится на

Наименьшее общее кратное группы, содержащей это число, будет делиться на а НОК оставшейся группы — не будет. Значит, сумма этих НОК не делится на с другой стороны, эта сумма больше чем Поэтому эта сумма не может быть степенью двойки.

Среди пяти подряд идущих натуральных чисел могут найтись интересных числа. Например, суммы цифр чисел равны и Все пять чисел оказаться интересными не могут. Среди наших этих пяти чисел есть три, лежащих в одном десятке. Их суммы цифр – последовательные числа; значит, все они не могут одновременно быть простыми. Действительно, хотя бы одно из них четно, значит равняется 2. Тогда последовательность из трех сумм цифр это либо либо и ни одна из них не состоит из простых чисел.

Решение 1.

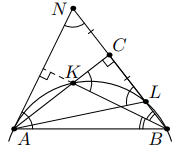
Отложим на продолжении за точку отрезок Тогда и нам надо доказать, что

Так как четырёхугольник вписан, имеем

С другой стороны, прямоугольные треугольники и равны по двум катетам, так что Тогда из треугольника имеем

Из полученного равенства и следует, что

Решение 2.

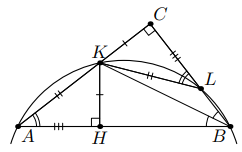
Опустим из точки перпендикуляр на гипотенузу Прямоугольные треугольники и равны по гипотенузе и острому углу ( Значит, и Далее, в окружности, описанной около на хорды и опираются равные углы, поэтому Значит, прямоугольные треугольники и равны по катету и гипотенузе, откуда Итак, что и требовалось доказать.

Первое решение. Обозначим Назовём последовательность из натуральных чисел, любые два соседних члена которой различаются не больше, чем на интересной. Каждой интересной последовательности сопоставим разностную последовательность Все члены разностной последовательности равны или так что количество всевозможных разностных последовательностей равно

Посчитаем сначала количество всех интересных последовательностей, минимальный член которых не превосходит Рассмотрим произвольную разностную последовательность Любые две интересные последовательности, соответствующие ей, отличаются прибавлением одного и того же числа к каждому члену. Значит, среди них ровно по одной последовательности с минимальным членом, равным и Таким образом,

В учтены все последовательности, выписываемые Петей, и несколько лишних - тех, в которых не встречается Ясно, что, если в интересной последовательности встречаются как числа, большие так и меньшие то и тоже встречается. Но минимальный член каждой лишней последовательности не больше значит, и все их члены не превосходят Итак, все лишние последовательности состоят из единиц и двоек. С другой стороны, каждая последовательность из единиц и двоек является интересной, и, стало быть, лишней.

Итого, лишних последовательностей ровно а значит, искомое количество равно

Второе решение. Назовём хорошей последовательность из натуральных чисел, в которой хотя бы раз встречается тройка, а любые два соседних члена различаются не больше, чем на Обозначим через количество хороших последовательностей длины Мы докажем индукцией по что База индукции при очевидна.

Сделаем переход от к Назовём хорошую членную последовательность отличной, если среди первых её членов встречается тройка. Откинем от каждой отличной последовательности её последний член; в каждом случае мы получим хорошую -членную последовательность. При этом, если хорошая -членная последовательность оканчивается числом то она получается таким образом из двух отличных — оканчивающихся числом или Если же оканчивается числом то она получается из трёх отличных, у которых в конце стоит или Итак, если количество -членных хороших последовательностей, оканчивающихся числом равно то количество отличных -членных последовательностей равно

Осталось посчитать количество неотличных -членных последовательностей. Ясно, что каждая из них оканчивается числом если эту тройку откинуть, получится -членная последовательность без троек. Поскольку её соседние члены отличаются не больше, чем на то либо все они больше либо все меньше

Если все члены меньше то состоит из чисел и оканчиваясь числом При этом любая такая последовательность, дополненная в конце тройкой, даст хорошую. Значит, такие последовательности получаются ровно из неотличных.

Пусть теперь все члены больше тогда она оканчивается на четвёрку. Вычтя из всех её членов по мы получим либо хорошую последовательность, оканчивающуюся числом (если в полученной последовательности содержится ) — таких ровно либо последовательность из единиц и двоек, оканчивающуюся числом — таких ровно Итого, последовательностей последнего типа есть

В итоге мы получаем, что Переход доказан.

Вспомним одно из свойств ортоцентра: точка пересечения высот треугольника является точкой пересечения биссектрис ортотреугольника

Доказательство: счет вписанных углов

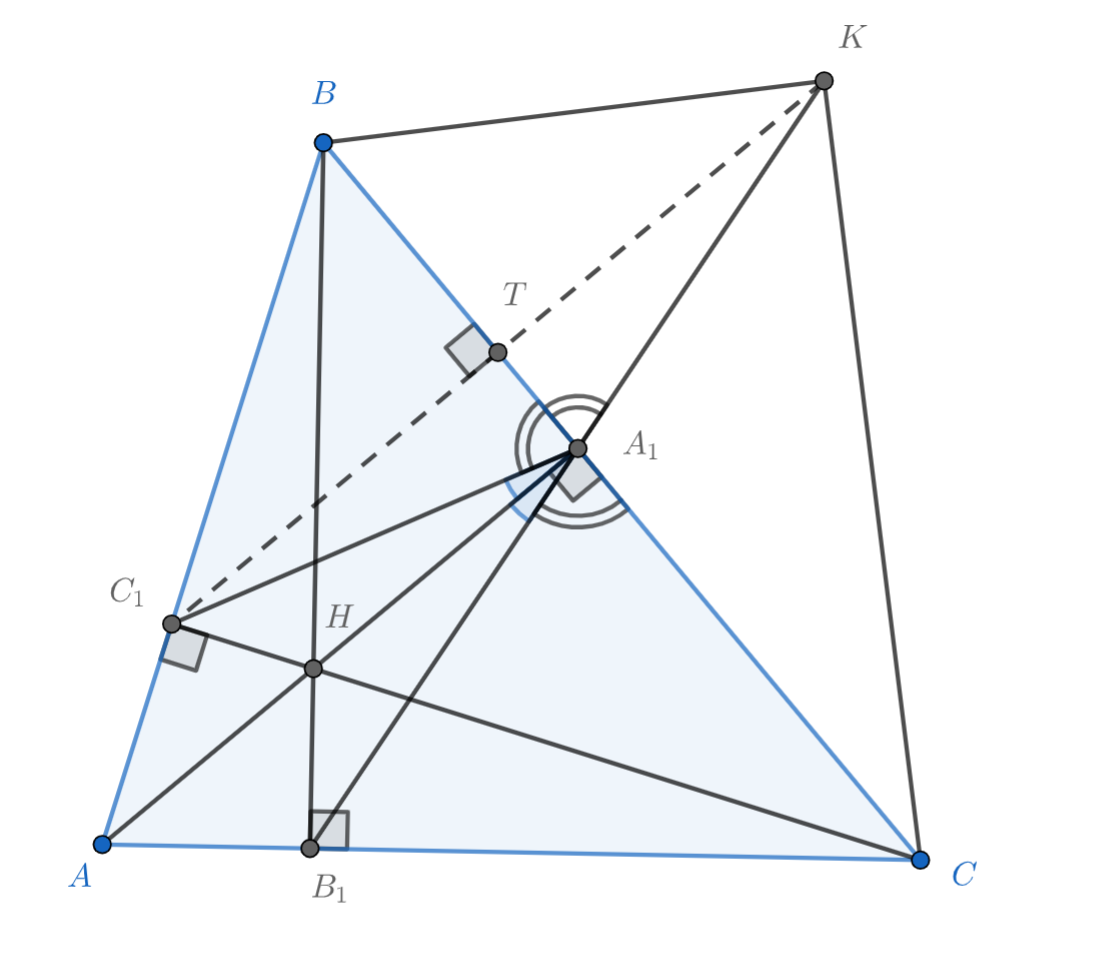
Пусть Проведем и применим факт выше

Пусть описанная окружность треугольника является единичной с центром в нуле, а также треугольник положительно ориентирован. Пусть — комплексное число с единичным модулем, такое, что попадает в середину дуги и попадает в точку аналогично определим число (— середина дуги совпадает с ). Тогда середина дуги имеет координату Центр вписанной окружности имеет координату (как было доказано на вебинаре). Точка имеет координату Осталось проверить, что число — вещественное. Подставив все найденные выражения, получаем

Последнее выражение действительно вещественное, что легко видно после замены ,

Обозначим за сумму цифр числа При сложении чисел сумма цифр не увеличивается, а при умножении на 10 сумма цифр не меняется, поэтому

Значит, в неравенстве должно достигаться равенство. Это произойдёт, если при сложении с не будет переносов через разряд.

Предположим, что нечётно. Значит, оканчивается нечётной цифрой. Заметим, что произведение и любой нечётной цифры оканчивается на , но тогда и оканчивается на . В таком случае при суммировании и перенос произойдёт при сложении цифр в разряде единиц. Пришли к противоречию. Значит, не может быть нечётным.

Обозначим цифры, выписываемые игроками, последовательно через цифры с нечётными номерами выписывает первый, а с чётными — второй. Рассмотрим остатки от деления на знакопеременных сумм

Согласно признаку делимости на после го хода на доске возникнет число, кратное тогда и только тогда, когда совпадает с одним из Расположим эти остатки по кругу по часовой стрелке от до и изобразим последовательность ходов как процесс перемещения по кругу по неповторяющимся остаткам При этом первый игрок м ходом "прибавляет"к любое число от до а второй — любое число от до Таким образом, кроме повтора уже встречавшегося остатка, первому игроку запрещён ход против часовой стрелки на а второму — ход по часовой стрелке на После го хода свободными останутся остатков. Игрок гарантированно может сделать ход, если есть хотя бы два свободных остатка, значит, первые восемь ходов игроки сделать смогут, а й ход сделать нельзя никогда.

Рассмотрим ситуацию после седьмого хода (это ход первого), когда свободны остатка. Разберём три случая.

Свободные остатки расположены подряд: Тогда второй выписывает число с остатком (занимает остаток ), первый — а второй и выигрывает.

Остатки расположены так: два рядом — и один отдельно — Тогда второй занимает один из остатков далее либо первый занимает остаток второй — и выигрывает, либо первый занимает а второй — один из оставшихся и выигрывает.

Никакие два остатка не стоят рядом: Тогда второй может занять один из них и после хода первого, второй может занять последний свободный остаток и выиграть.

Первое решение.

Пусть Отсюда и

Поскольку — середина дуги то и (в силу равны ). Поэтому откуда и следует вписанность

______________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим углы треугольника как . Проведем — медиану, биссектрису и высоту равнобедренного треугольника . Докажем, что .

так как — серединный перпендикуляр к .

так как как вписанные, опирающиеся на одну дугу . Итого

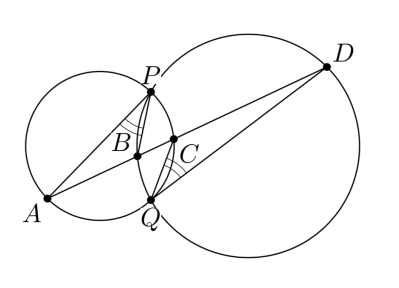
Вписанные в левую окружность углы, опирающиеся на дугу равны:

Так как — внешний угол треугольника то

Вписанные в правую окружность углы, опирающиеся на дугу равны:

Угол равен сумме углов и таким образом,

Получаем

Первое решение.

Пусть (равны как вписанные). Тогда и в силу равенства выполнено

Пусть и пересекаются в точке , отсюда

Второе решение.

Пусть касательная к окружности , проведённая через точку , пересекает окружность в точке , лежащей на дуге , не содержащей точки . Тогда . Поэтому , а так как как радиус, проведённый в точку касания, то .

Обозначим корни первого трёхчлена за и , а второго — за и (один корень общий по условию).

Первый трёхчлен можно записать в виде (по условию он приведённый) , а второй как .

Пусть существует положительное целое такое, что и .

Таким образом, и имеют общий делитель . По условию , так как и , но и взаимнопросты, а значит, оба числа на делиться не могут.

Запишем условие с помощью теоремы Виета: , , , . Из второго и третьего равенств следует, что .

Если , то и , тогда трёхчлены имеют вид и . Понятно, что они подходят к условию.

Пусть теперь , тогда в равенстве на можно сократить. Получим . Из этого следует, что . Таким образом, трёхчлены имеют вид и . Они оба имеют корень , значит этот же корень имеет их разность , то есть . ненулевое, значит , откуда .

Если , то трёхчлен имеет корень , то есть , но ненулевое, противоречие.

Если , то при трёхчлен равен , откуда и оба трёхчлена имеют вид .