Общее число равнозначных исходов расстановоки фигур есть выбор произвольных клеток из имеющихся , т.е. оно равно .

Благоприятный исход может в двух случаях: три одинаковые фигуры находятся на одной линии и одна не на этой линии, либо четыре одинаковых фигуры на одной линии. Тогда число благоприятных исходов для одной линии (горизонтали, вертикали или главной диагонали) равно . Всего имеется 18 различных линий (горизонталей, вертикалей и главных диагоналей). Итого число благоприятных исходов равно .

Искомая вероятность есть отношение числа благоприятных исходов к общему числу исходов:

Обозначение: — вероятность того, сделав } прыжков блоха отклоняется от на величину (отрицательные указывают, что блоха находится слева от положительные — справа, число соответствует точке ).

Свойства

1) для

2) (равновозможность направления прыжка)

3) попасть на прыжке в положение возможно по условию только из положений и с вероятностью поэтому

4) при фиксированном и всех, для Ниже приведена часть таблицы для определения

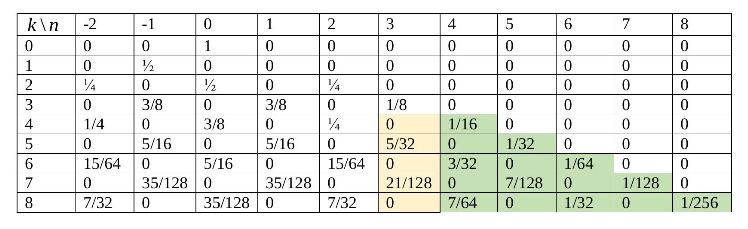
Вероятности, что Кузя закончил прыжки в точке записаны в столбце с номером и строками от до (отмечены желтым). Но Кузя побывал в точке и, если он закончил движение в точках расположенных правее (до включительно), соответствующие позиции отмечены зеленым. Однако Кузя мог, побывав в точке закончить движение и в симметричных относительно точках (т.е. слева от но с теми же вероятностями, что и справа от ), поэтому отмеченные зеленым вероятности надо умножить на Для числа те же.

Считаем, что количество прыжков от до равновероятно (с вероятностью ). Тогда суммируем вероятности, отмеченные желтым, добавляем удвоенные вероятности, отмеченные зеленым, результат умножаем на и на Получим

Используем рекуррентную формулу для поиска вероятности — получить сумму за бросков

Действительно, нам нужно откатиться на один бросок назад, в котором с равными вероятностями выпадают . Посчитаем таблицу вероятностей (не будем явно прописывать знаменатели , оставим только числители)

Бросать кубик имеет смысл только от до раз, иначе невозможно получить очков в сумме. Предположим, что каждое количество бросков равновероятно и наступает с вероятностью , получим формулу

Пусть в мешке было шоколадных и фруктовых. Найдём вероятность получить две шоколадные конфеты

По условию вероятность для одной шоколадной и одной фруктовой, которая равна

в три раза больше, так что . В итоге первое условие задачи эквивалентно нечётности (чтобы был целым).

По второму условию, включая Петю, конфеты брали ещё хотя бы детей. Каждый берёт по две конфеты, откуда

Случай прямая пересекает стороны квадрата

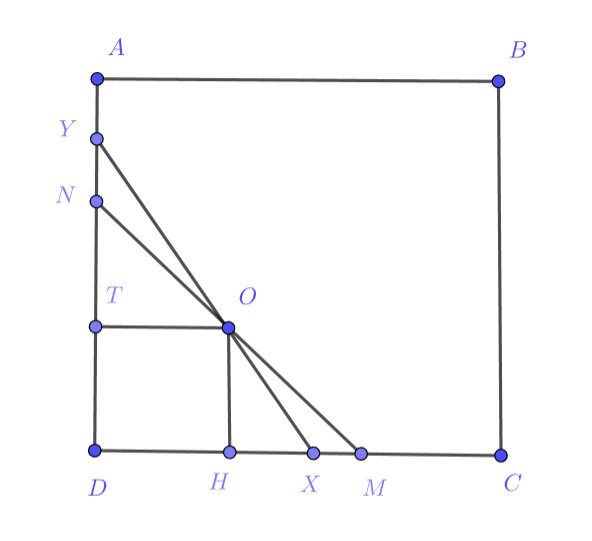
Пусть — проекции на стороны а в точках прямая пересекает эти стороны.

Обозначим С учётом и подобия получаем Запишем условие на площадь:

Мы выяснили, что нам подходят

и как раз соответствуют случаям, когда проходит через и и соответственно.

Случай прямая пересекается только с одной из сторон

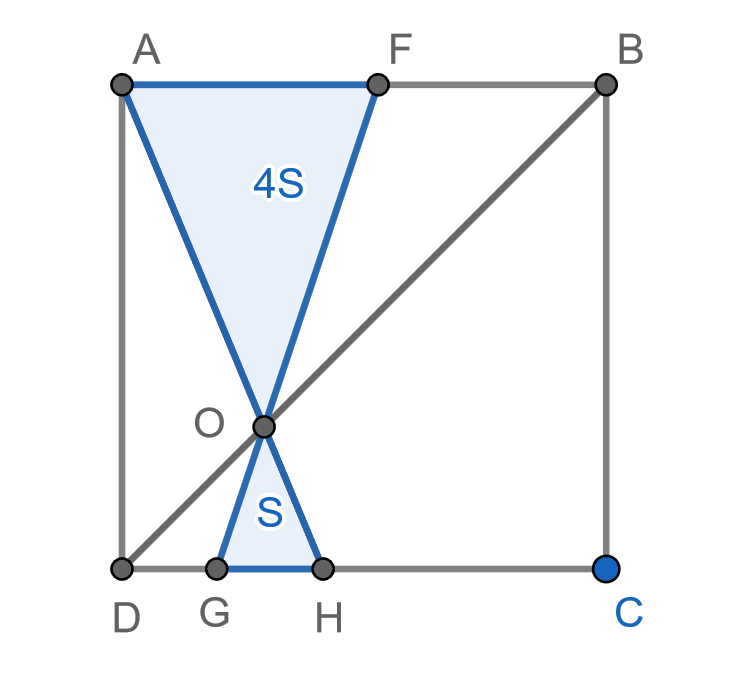
Покажем, что в таком случае площадь обоих частей Выше мы уже заметили, что в случае совпадения прямой с прямой или в случае совпадения с прямой площадь меньшей из отсекаемых частей в точности равна

Предположим, что прямая пересекает стороны Пусть она пересекает в точке в точке Треугольники подобны, при этом коэффициент подобия равен поэтому

Заметим, что если мы перейдем от прямой к прямой то площадь меньшей из частей увеличится на Но так как площадь то площадь

Случай, если пересекает стороны разбирается аналогично (просто рассматривается прямая вместо ).

В результате получаем ответ

Можно в числителе применить формулу разности арктангенсов

Обозначим . Тогда , где равномерно распределены на отрезке . Представим это в виде квадрата — выбор аналогичен выбору случайной точки из квадрата.

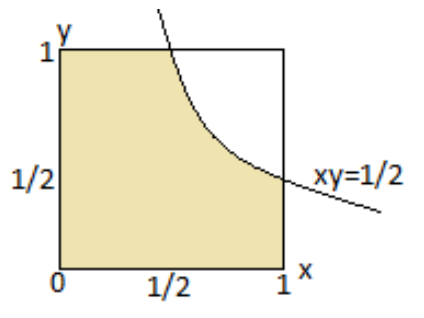
Нас интересует площадь под гиперболой внутри этого квадрата, которая равна

Обозначим . Тогда имеем условие , где равномерно распределены на отрезке . Представим это в виде квадрата — выбор аналогичен выбору случайной точки из квадрата:

Нас интересует площадь над гиперболой внутри этого квадрата.

Гипербола пересекается с прямой при , поэтому для искомой площади нам нужно из площади прямоугольника вычесть площадь под гиперболой, которая равна

Итак, получаем

Посчитаем сколько способов у робота попасть в каждую координату Понятно, что должно быть чётно. Всего робот делает шагов, при этом его суммарное смещение равно то есть шагов одного вида было ровно на больше. Имеем систему ( — число шагов вперёд, — назад)

Которая имеет единственное решение относительно После этого роботу достаточно выбрать номера шагов, на которых он идёт вперёд — способов это сделать Из условия возможны только в силу симметрии оставим только положительные. Всего при этом маршрутов у робота в итоге имеем вероятность

Замечание. Такой процесс называется одномерным симметричным случайным блужданием, формулу несложно обобщить до случая несимметричного умножая на вероятности шага в каждую сторону. Почему сумма вероятностей будет равна единице?

Заметим, что вероятность получить значение такая же, как и вероятность получить значение ведь соответствующие исходы для и можно разделить соответственно на пары троек где — число, выпавшее на -ом кубике, и Поэтому рассмотрим значения в пределах от до а для вероятность будет такая же.

Итак, нужно понять, какому соответствует большее число троек таких что

Поставим в ряд шаров, между ними будет позиций, куда мы будем ставить перегородки (на одну и ту же позицию ставить перегородки не разрешается). Количество шаров между перегородками и будет соответстовать

Количество способов поставить перегородки равно (возрастающая функция от ).

При при подсчёте мы получим различные перестановок тройки которые не соответствуют условию . При получим различные перестановки тройки и перестановок тройки которые не соответствуют условию

Итак, подходящих троек при будет при их при их

Наибольшая вероятность достигается при и

Заметим, что Петя выигрывает с вероятностью (подходят исходы — их из ). Справедливая цена игра означает, что Петя имеет нулевой средний выигрыш, то есть

Возможны три несовместных случая, разберём каждый и сложим вероятности.

• Вася промахнулся только один раз — из рогатки. С учётом порядка этого промаха из двух выстрелов имеем вероятность

  

• Вася промахнулся только один раз — из пистолета. Аналогично получаем

  

• Был только один промах — из ружья. Здесь

  

В итоге

Всего способов покрасить вершин кубика в цвета, то есть разделить на две группы по вершины, имеется штук.

Из них есть , когда жёлтые вершины окажутся в плоскости одной грани (потому что всего граней ). Так что вероятность того, что в кубе окажется "жёлтая"грань равна

При этом вероятность попадания нужной "жёлтой"грани (при условии того, что она есть) равна . Откуда по формуле условной вероятности искомая вероятность равна .