Ошибка.
Попробуйте повторить позже
Лес представляет собой координатную плоскость, в некоторых узлах которой растут ёлки. Всего ёлок больше миллиона. Докажите, что можно срубить более 100000 ёлок так, чтобы расстояние между любыми двумя срубленными ёлками было больше 3. (Узлом называется точка, обе координаты которой целые; ёлки считаем точками.)
Источники:
Раскрасим узлы в 10 цветов так, чтобы узлы одного цвета образовывали сетку из квадратов со стороной . Например, пусть цвет узла с
координатами (
) определяется остатком от деления числа
на 10 (считаем, что деревья растут в центрах
квадратов):
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
| 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 |
| 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 |
| 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 | 1 | 2 | 3 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
По принципу Дирихле, в какой-то из десяти цветов окрасились более 100 тысяч ёлок. Тогда все эти ёлки можно срубить, поскольку
расстояние между любыми двумя из них не меньше .
Ошибка.
Попробуйте повторить позже
Внутри правильного шестиугольника со стороной 1 расположено 7 точек. Докажите, что среди них найдутся две точки на расстоянии не больше 1.
Правильный шестиугольник можно разбить на шесть правильных треугольников со стороной 1. Тогда хотя бы в одном из этих треугольников будет лежать две отмеченные точки. Расстояние между ними не будет превосходить стороны треугольника.
Ошибка.
Попробуйте повторить позже
Сколько точек пространства с целочисленными координатами принадлежат треугольнику с вершинами ,
,
? Точка
на вершинах и сторонах тоже считаются.
Источники:
Подсказка 1
Давайте немного упростим задачу и сдвинем одну из вершин в начало координат, чтобы числа стали попроще, для этого можно сделать параллельный перенос на вектор (-3;-4;-5), а как можно посчитать кол-во целочисленных точек на стороне?
Подсказка 2
Верно, кол-во целых точек (включая концы) на отрезке (x₁,y₁,z₁), (x₂,y₂,z₂), это НОД(|x₁-x₂|, |y₁-y₂|, |z₁-z₂|) + 1, итак, когда мы знаем кол-во точек на периметре треугольника, давайте перейдём к его внутренности, если взять произвольную целочисленную точку, можно ли получить какое-то следствие, которое было бы легче проверить, но оно бы оставило нам пару точек для перебора?
Подсказка 3
Да, можно сказать, что если точка A была подходящей, то точка A' полученная проецированием её на одну из плоскостей тоже будет подходить, а значит можно спроецировать весь треугольник, например, на плоскость Oxy и найти возможных кандидатов там, а потом проверить только их
Подсказка 4
Для проверки наших кандидатов можно составить систему уравнений из двух векторов, образующих стороны, с положительными коэффициентами, сумма которых меньше 1, чтобы получить точку внутри треугольника, остаётся проверить, что найдутся целые решения, которые бы удовлетворяли полученной системе
Подсказка 5
Для удобства можно выразить из первых двух уравнений коэффициенты и подставить их в третье уравнение, тогда останется лишь условие на координаты точек, но предыдущие ограничения всё ещё следует проверить
Перенесём треугольник одной вершиной в начало координат. Тогда его можно представлять как точку , из которой выходят вектора
и
.
Тогда внутренность треугольника можно представить как где
— действительные числа,
и
Вопрос о целых точках на треугольнике, получается, стоит так: при каких целых система:
имеет решения , удовлетворяющие условиям выше.
Мы выделили внутренность, потому что стороны легче рассмотреть отдельно. Три целочисленные вершины лежат в треугольнике по
определению. На сторонах точки подсчитать тоже просто — стороны это вектора и третья сторона
.
Получить целочисленную точку можно только на середине вектора
, а у остальных сторон нет общих делителей координат, и через целые
точки они не проходят. Значит, на периметре лежат
точки.
Переходим к внутренней части треугольника. Конечно, нет гарантий, что там будет хотя бы одна целочисленная точка —
но если такая есть, то её проекции на координатные плоскости тоже будут целочисленные. Поэтому давайте рассмотрим
проекцию треугольника на плоскость , и отберём на ней потенциально подходящие пары
а после выкинем
лишние.
Проецируем треугольник на — получается треугольник на плоскости с вершинами
Внутрь него точки попадут
такие:
Решаем систему, состоящую из двух первых уравнений:
Получаем следующие решения:
Полученные значения подставляются в третье уравнение
, и если
оказывается целым — точка найдена. После
подстановки получается выражение:
то есть должна быть чётной. Из
кандидатов подойдут только
.
Плюс точки на сторонах, и всего точек на треугольнике
Ошибка.
Попробуйте повторить позже
На плоскости отмечено 100 точек общего положения (т.е. никакие три не лежат на одной прямой). Докажите, что можно выбрать три
отмеченные точки ,
,
так, чтобы для любой точки
из оставшихся 97 отмеченных точек, прямые
и
не содержали бы
точек, лежащих внутри треугольника
.
Подсказка 1
Прямые, соединяющие точки A, B, CЮ делят плоскость на 7 частей, включая треугольник внутри. Рассмотрите эти части. Точки D из каких частей нам подходят?
Подсказка 2
Видно, что подходящие части тем больше, чем больше угол АВС. Воспользуемся принципом крайнего и возьмём такие 3 точки, чтобы АВС был максимальным. Проверим, подходит ли нам этот случай, пойдя от противного: пусть они не подходят. Тогда в каких частях может находиться точка D?
Подсказка 3
Верно, а теперь попробуйте получить противоречие через сумму углов, зная, что угол АВС максимальный из всех возможных
Применим принцип крайнего: выберем среди всех троек точек треугольник с самым большим углом
Предположим, что точки ,
,
не подходят. Тогда существует точка
в объединении частей плоскости, одна из которых
заключена между прямыми
и
а другая — между прямыми
и
При этом не может лежать внутри треугольника
, иначе
.
Рассмотрим случай, когда лежит между лучами
и
(когда
и
лежат в разных полуплоскостях относительно
).
Тогда
получаем противоречие. То же работает для случая, когда лежит между лучами
и
.
Оставшиеся два случая (когда и
лежат в разных полуплоскостях относительно
) рассматриваются аналогично: в
них
Ошибка.
Попробуйте повторить позже
В таблице отметили
клеток. Для какого наименьшего
гарантированно можно выбрать
отмеченные клетки, центры которых
образуют прямоугольный треугольник?
Сначала покажем, что можно отметить не более клетки так, чтобы никакие
клетки не образовывали треугольник. Выберем в
таблице центры всех клеток нижней строки и правого столбца, за исключением правой нижней угловой клетки. Всего выбрано
точки, и каждая тройка отмеченных точек образует тупоугольный треугольник.
Докажем, что больше центров клеток выбрать нельзя. Для каждого отмеченного центра либо в его строке, либо в его столбце
других отмеченных центров нет. Пометим этот ряд. Если помечены все строки, то выбрано всего не больше
центров.
Аналогична ситуация, когда помечены все столбцы.
Если же помечены не все строки и не все столбцы, то всего отмечено не более строк и не более
столбцов:
Отсюда следует ответ
Ошибка.
Попробуйте повторить позже
Есть точек,
из которых лежат на одной окружности в плоскости
, а остальные 5 вне
. Известно, что если четыре точки из всех
лежат в одной плоскости, то эта плоскость —
Сколько существует выпуклых пирамид с вершинами в этих точках? (Пирамиды
считаются различными, если их множества вершин различны.)
Источники:
Подсказка 1
Среди всех возможных пирамид для нас принципиально различаются два случая: когда вершин 4 (тетраэдр) и больше. Посчитаем их по отдельности и затем сложим.
Подсказка 2
Количество всех возможных тетраэдров - количество способов выбрать 4 вершины, за исключением случаев, когда все точки лежат в одной плоскости. Из условия нам известно, что это возможно только когда все 4 вершины принадлежат плоскости 𝜶.
Подсказка 3
У n-угольной пирамиды, где n≥4 основание лежит в плоскости 𝜶, а вершина вне неё. Отдельно посчитаем способы выбрать основание и умножим на количество вариантов выбора вершин.
Подсказка 4
Количество способов выбрать основание находится как сумма числа сочетаний из 7 от 4 до 7, а вершину пирамиды можно взять пятью разными способами. Тогда нужно просто перемножить их и сложить найденное количество тетраэдров и n-угольных пирамид с n≥4
Посчитаем отдельно количество тетраэдров и выпуклых угольных пирамид с
Количество тетраэдров это количество способов выбрать точки, не лежащих одновременно в одной плоскости. Тогда количество
тетраэдров равняется
Найдем количество выпуклых угольных пирамид с
Основание такой пирамиды лежит в плоскости
а вершина —
вне
Тогда посчитаем количество оснований. Надо просуммировать все способы выбрать от 4 до 7 вершин без учёта
порядка
Для каждого из посчитанных оснований вершину пирамиды можно выбрать пятью способами, поэтому всего пирамид
Итоговый ответ
Ошибка.
Попробуйте повторить позже
Дан белый клетчатый прямоугольник . Сколькими способами можно покрасить 8 его клеток в чёрный цвет так, чтобы
покрашенное множество клеток было симметрично относительно центра прямоугольника либо одной из его “средних линий”
прямоугольника (“средней линией” прямоугольника назовём отрезок, соединяющий середины двух его противоположных
сторон). Ответ дайте в виде выражения, содержащего не более трёх членов (в них могут входить факториалы, биномиальные
коэффициенты).
Источники:
Подсказка 1
Давайте начнём распутывать клубок симметрий с того, что обозначим за A₁ множество восьмёрок симметричных относительно одной горизонтальной средний линии, за A₂ - вертикальной, за B - относительно центра прямоугольника. Давайте подумаем, сколько нам нужно зафиксировать точек для каждой из симметрий и где, чтобы однозначно восстановить всю восьмёрку?
Подсказка 2
Верно, для A₁ нужны 4 точки не выше (не ниже), чем горизонтальная средняя линия, для A₂ - 4 точки не правее (не левее), чем вертикальная средняя линия, для B - 4 точки в любой одной из указанных ранее областей. Теперь стоит задуматься о том, пересекаются ли данные множества или какая-то комбинация симметрий даёт другую симметрию?
Подсказка 3
Верно, если восьмёрка лежит в любых двух множества A₁, A₂, B, то она лежит во всех трёх, отсюда, вспоминая формулу включений-исключений, мы понимаем, что ответ уже очень близко, осталось только его расписать.
Назовем восьмеркой набор из клеток. Пусть
— множество восьмерок, симметричных относительной
,
— относительно
,
— относительно центра прямоугольника.
и
это средние линии прямоугольника.
Если выбрать какие-то точки в верхней половине прямоугольника, то остальные точки легко находятся в силу одной из
рассматриваемой симметрий относительно
и центра прямоугольника. Тогда количество элементов во множествах
будет
одинаковым. Тогда количество элементов в
будет равно количеству способов выбрать
очки в одной половине фигуры
относительно
Остальные
точки будут располагаются в другой половине. Тогда количество способов равняется
Если восьмерка лежит сразу в из
множеств
то она лежит и в третьей. Это значит, что пересечение двух множеств или
пусто, или пересекается с третьим.
Чтобы найти ответ надо найти количество элементов в объединении множеств. Используя формулу включений-исключений, получаем, что
где — означает количество элементов во множестве
— искомое число
Если точки, лежащие в одной из четвертей прямоугольника, принадлежат пересечению всех
множеств, то легко восстановить
исходную восьмерку, удовлетворяющую сразу трем симметриям. Тогда можно посчитать количество элементов в пересечении множеств. Это
будет количество способов выбрать
точки в одной из четвертей прямоугольника, образованной
и центром прямоугольника.
Следовательно, количество элементов равняется
Тогда посчитаем
Ошибка.
Попробуйте повторить позже
На плоскости дано множество из точек. Для любых
его точек можно выбрать две окружности так, что все эти точки окажутся на
выбранных окружностях. Докажите, что все
точек лежат на двух окружностях.
Так как любые точек лежат на двух окружностях, то найдется окружность
на которой лежит не менее
точек. Рассмотрим все
точки множества, не лежащие на
Если таких точек четыре или меньше, то утверждение задачи верно. Действительно, дополнив их
точками окружности
до девяти, получим, что они лежат на двух окружностях, на одной из которых лежат три дополняющих точки,
поэтому это
Значит, все наши точки лежат на другой окружности. Пусть вне окружности
лежит не менее пяти точек. Возьмем пять
точек
на
и три точки
вне
Через точки
проходит единственная окружность
Возьмем точку
отличную от точек
По условию существуют две окружности
и
содержащие все точки
Тогда опять одна из окружностей
и
совпадает с
Поскольку точки
не
лежат на окружности
все они оказываются на той из окружностей
или
которая не совпадает с
и эта
вторая окружность тем самым совпадает с
Получается, что точка
лежит либо на
либо на
что завершает
доказательство.
Ошибка.
Попробуйте повторить позже
На окружности расположено синих точек, а внутри окружности несколько красных таким образом, что никакие
точки не
лежат на одной прямой. Оказалось, что существует
треугольника с синими вершинами, содержащих ровно по
красных точек. Докажите, что остальные
треугольников с синими вершинами тоже содержат ровно по
красных
точек.
Прежде всего прокомментируем условие задачи. Количество треугольников с синими вершинами равно поэтому “остальных”
треугольников действительно
Выберем любой треугольник для которого еще не известно, сколько в нем точек. Такие треугольники будем называть плохими.
Заметим, что для любых четырех синих точек среди четырех треугольников, образованных тройками этих точек, не может ровно один быть
плохим. Рассмотрим
четверок синих точек, среди которых есть все вершины треугольника
Тогда для каждой такой четверки
найдется плохой треугольник, отличный от
Но все эти плохие треугольники различны, что противоречит тому, что плохих
треугольников не более
Значит, их нет вообще.
Ошибка.
Попробуйте повторить позже
Куб состоит из единичных кубиков. Рассмотрим всевозможные кубы, содержащиеся в этом кубе и составленные из
единичных кубиков. Будем говорить, что один такой куб содержится внутри другого такого куба, если все его кубики принадлежат другому
кубу и не лежат на его гранях. Какое наибольшее количество кубов со стороной больше
можно выбрать так, чтобы ни один из них не
содержался внутри другого?
Рассмотрим пример, подходящий под условие, с максимальным количеством кубов. Выберем из всех кубов в этом примере
наибольший куб пусть его сторона равна
и при этом
Тогда заменим этот куб
на куб
со стороной
лежащий строго внутри
Покажем, почему новый пример также подходит под все условия. Во-первых, куба
в примере еще не было, так как иначе
лежал строго внутри
Далее, если какой-то куб
лежит строго внутри
то и до этого куб
лежал внутри куба
что противоречит условию. Пусть, наоборот, сам куб
лежит внутри
какого-то куба
Тогда сторона этого куба
не меньше
с другой стороны,
максимальная сторона всех кубов,
поэтому сторона
в точности равна
Но единственный куб со стороной
строго внутри которого лежит
это
собственно куб
а мы его из примера удалили. Поэтому такая ситуация невозможна, и значит новый набор кубов также
подходит под все условия. Будем описанным выше образом заменять кубы на меньшие, пока не закончатся кубы со сторонами,
большими
В конце стороны всех кубов будут равны
или
а таких кубов не больше
Осталось
убедиться, что набор всех кубов со сторонами
и
очевидно, подходит под условие задачи, значит, ответ в точности
Ошибка.
Попробуйте повторить позже
На плоскости дано точек общего положения, одна из них синяя, остальные красные. Докажите, что количество треугольников с
вершинами в красных точках, содержащих синюю, чётно.
Начнем перемещать синюю точку по прямой, не содержащей красные точки. Остановимся тогда, когда она пересечет первый отрезок с
концами в красных точках, но еще не дойдет до второго. Если такого момента времени не существует, значит синяя точка не лежит ни в
одном красном треугольнике (любая прямая, проведенная через синюю точку, пересекла бы его стороны), и утверждение задачи очевидно.
Назовем вершины пересеченного отрезка и
Сравним количество треугольников, содержащих синюю точку в исходном ее положении и после перемещения. Ясно что любой
треугольник, не содержащий сторону либо содержал синюю точку оба раза, либо не содержал, так как синяя точка не пересекла на
своем пути ни одну из его сторон. Рассмотрим полуплоскость относительно
в которой изначально располагалась синяя точка.
Утверждается, что треугольник со стороной
и третьей вершиной в любой красной точке этой полуплоскости содержал синюю точку в
ее исходном положении. Действительно, в противном случае отрезок, соединяющий исходное положение синей точки и
точку, в которой траектория ее движения пересекает
пересекает и некоторую сторону этого треугольника. Ясно,
что никакой треугольник со стороной
и вершиной в другой полуплоскости не содержит исходное положение синей
точки. Теперь рассмотрим другую полуплоскость относительно
– в которой располагается синяя точка в момент
остановки. Аналогично, треугольник со стороной
и любой вершиной этой полуплоскости содержит синюю точку после
перемещения.
Если в полуплоскости, в которой изначально находилась синяя точка, красных вершин, то ясно, что в другой полуплоскости их
а количество треугольников, содержащих синюю точку, при описанном перемещении изменилось на
Так как это число
четное, мы доказали, что описанная операция не меняет четности количества треугольников, содержащих синюю точку. Будем повторять
эту операцию до тех пор, пока синяя точка не выйдет за пределы выпуклой оболочки множества красных точек. Ясно, что когда этот
момент наступит, не будет существовать ни одного красного треугольника, содержащего синюю точку, то есть в конце четное количество
треугольников с вершинами в красных точках содержит синюю. Значит, изначально количество таких треугольников тоже было
четным.
Ошибка.
Попробуйте повторить позже
Докажите, что любой треугольник можно разрезать на прямоугольных треугольников.
Докажем индукцией по что при
любой треугольник можно разрезать на
прямоугольных треугольников. База для
очевидно, просто проведём высоту (если треугольник прямоугольный, проведём из прямого угла).
Переход. Воспользуемся предположением и разделим треугольник на прямоугольных треугольников. Среди полученных
треугольников выберем любой и разделим его на два прямоугольных. Получили разделение на
прямоугольный
треугольник.
Ошибка.
Попробуйте повторить позже
Окружность разбита точками на равные дуги. Докажите, что у любой замкнутой
-звенной ломаной с вершинами во всех этих точках
есть хотя бы два параллельных звена.
Занумеруем точки по порядку остатками при делении на
и рассмотрим ломаную с вершинами в этих точках. На
каждом ее звене запишем сумму чисел, стоящих в концах звена. Легко проверить очень простой критерий параллельности звеньев: числа,
записанные на них, дают равные остатки при делении на
Предположив, что параллельных звеньев нет, получим, что на звеньях
написаны разные остатки при делении на
т.е. сумма всех таких остатков равна
С другой стороны,
сумма чисел на всех звеньях - это удвоенная сумма чисел, написанных на всех вершинах (каждая вершина «отдает» свой номер двум
звеньям). Получаем, что
и
должны давать один остаток при делении на
Но тогда
должно делиться на
что
невозможно — получаем противоречие.
Ошибка.
Попробуйте повторить позже
Существует ли многоугольник, не имеющий центра симметрии, который можно разрезать на два выпуклых многоугольника, каждый из которых имеет центр симметрии?
Источники:
Подсказка 1
Придумывать что-то очень сложное не хочется, поэтому думаем, а на какие простые фигуры, имеющие центр симметрии, хочется разбить наш многоугольник?
Подсказка 2
На прямоугольники! Составим фигуру из них)
Пример:
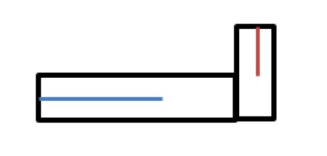
Пример подходит, потому что центрами симметрии прямоугольников являются точки пересечения их диагоналей, а данный многоугольник не имеет центра симметрии, так как если он лежит вне синего отрезка, проходящего через середину одной из сторон, левые вершины многоугольника перейдут не в точки многоугольника, а если он лежит вне красного отрезка, проходящего через середину другой стороны, то верхние вершины многоугольника перейдут не в точки многоугольника.
Ошибка.
Попробуйте повторить позже
Каждый из шести домов, стоящих на одной стороне улицы, соединен кабельными воздушными линиями с каждым из восьми домов на противоположной стороне. Сколько попарных пересечений образуют тени этих кабелей на поверхности улицы, если никакие три из них не пересекаются в одной точке? Считайте, что свет, порождающий эти тени, падает вертикально вниз.
Источники:
Подсказка 1
Нас просят найти количество попарных пересечений! Для начала давайте разберемся, а когда образуется одно попарное пересечение?
Подсказка 2
Да, пересечение образуется, когда мы выбираем два дома на одной стороне(различных), два дома на другой стороне(тоже различных) и делаем биекцию между ними(то есть, соединяем один дом ровно с одним другим). Остаётся посчитать количество таких четверок домов!
Подсказка 3
Первые два дома нужно выбрать из 6, а вторые два из 8. То есть, это просто число сочетаний из 6 по 2 и число сочетаний из 8 по 2!
Возьмем произвольную пару домов на одной стороне улицы и произвольную пару на другой. Они являются вершинами выпуклого
четырехугольника (поскольку две стороны четырехугольника, идущие от каждой выбранной пары, лежат по одну сторону прямой, т.е. углы
не превосходят ), следовательно, его диагонали пересекаются.
Каждое попарное пресечение теней (кабелей) является точкой пересечения диагоналей такого четырехугольника. Таким образом, осталось найти их количество, которое равно произведению способов выбрать пару домов на каждой стороне улицы.
Ошибка.
Попробуйте повторить позже
Дано несколько прямоугольных параллелепипедов в пространстве. Известно, что у каждой пары параллелепипедов есть хотя бы одна общая точка, а их рёбра соответственно параллельны. Обязательно ли все параллелепипеды имеют общую точку?
Источники:
Подсказка 1
Если попытаться построить пример, то не особо получится, что у них у всех нет общей точки...Стоит попробовать доказать, что она всегда есть! Что можно сделать для этого?
Подсказка 2
При построении примера, скорее всего, были ещё трудности: в пространстве сложно нормально нарисовать картинку....Так, давайте спроецируем всё, например, на одну из координатных осей, т.к. это параллелепипеды и у них соответствующие ребра параллельны) Как теперь будет выглядеть условие?
Подсказка 3
Теперь у нас на прямой есть отрезки вида [ai, bi], и каждые два из них пересекаются. Чтобы доказать, что у них всех есть общая точка, посмотрите на конфигурацию, где вы понимаете, что у них у всех есть непустое пересечение)
Подсказка 4
Ну и осталось просто сказать это для всех трех координатных осей. Задача решена!
Поскольку у параллелепипедов ребра соответственно параллельны, мы можем ввести декартову систему координат, направив оси вдоль трех
ребер, смежных с одной вершиной (которая станет началом координат) выбранного параллелепипеда. В этой системе координат ребра всех
параллелепипедов будут параллельны осям. Спроектировав на ось Ох данный -ый параллелепипед
получим отрезок,
который обозначим
Любая пара таких отрезков имеет непустое пересечение (в противном случае соответствующая пара
параллелепипедов не пересекается).
Таким образом, приходим к такой задаче: на числовой прямой есть попарно пересекающиеся отрезки и требуется
доказать, что у них имеется общая точка. Опытные олимпиадники могут сразу сослаться на теорему Хелли. Мы же приведём её
доказательство, чтобы не оставлять у неопытных читателей чувство неловкости.
Пусть – наибольшее значение среди левых концов отрезков, т.е.
и аналогично, пусть
— наименьшее
значение среди правых концов отрезков. Тогда
так как в противном случае
для некоторых
и
а значит,
-ый и
-ый отрезки не пересекаются. Отсюда следует, что любая точка отрезка
будет общей для всех наших
отрезков. Итак, пусть точка
принадлежит проекциям на ось Ох всех параллелепипедов. Точно так же мы можем
найти общие точки
и
проекций на оси Oy и Oz. Тогда точка с координатами
будет принадлежать всем
параллелепипедам.
Ошибка.
Попробуйте повторить позже
На прямой выбрано несколько отрезков так, что всех их концы различны. Докажите, что на этой прямой можно отметить несколько точек так, чтобы на каждом отрезке было отмечено нечётное количество отмеченных точек.
Источники:
Подсказка 1
Очень часто в задачах на отрезки, где не указано из количество, помогает индукция) Попробуем начать с маленького количество отрезков, как-то порисуем и поймем, как переходить к большему количеству.
Подсказка 2
На одном отрезке достаточно отметить одну точку. Что происходит на двух? Мы ставим точку на какой-то отрезок. Если условие для второго еще не выполнено, ставим другую точку. А что, если такой же алгоритм придумать для большего количества чисел по индукции на количество отрезков?)
Пусть выбрано отрезков. Докажем утверждение методом математической индукции по
- 1.
-
База: Для одного отрезка просто отметим его правый конец.
- 2.
-
Переход: Пусть мы можем так отмечать для
отрезков. Докажем, что мы сможем так сделать для
отрезков. Для этого рассмотрим отрезок, у которого конец находится правее всех концов других отрезков. Далее «забудем» про этот отрезок, и для оставшихся отрезков применим предположение. Теперь «вспомним» отрезок. Если он содержит нечетное число отмеченных точек, то мы смогли отметить точки нужным образом. Если же это не так, то дополнительно отметим его конец, так как он самый правый, то остальные отрезки его не содержат и мы получим требуемое.
Ошибка.
Попробуйте повторить позже
Есть два ряда — верхний и нижний, каждый из 6 точек (см. рисунок). Проводят отрезки с концами в противоположных рядах так, чтобы из каждой точки выходил ровно один отрезок. Сколько существует способов провести отрезки, чтобы среди всех пар отрезков было ровно 7 пар пересекающихся отрезков?
Источники:
Подсказка 1
В таких задачах полезно посмотреть на случаи поменьше, с меньшим количеством отрезков и необходимых пересечений
Подсказка 2
Когда два отрезка пересекаются? Когда начало первого левее, чем начало второго, а конец первого правее, чем конец второго
Подсказка 3
Давайте посмотрим, что меняется, когда мы добавляем еще один отрезок.
Подсказка 4
Мы можем поставить второй конец в самую правую точку. Тогда у нас останется k пересечений.
Подсказка 5
Давайте подумаем, из каких расстановок отрезков для 5 пар точек мы можем получить необходимую расстановку для 6 пар точек.
Подсказка 6
Общая формула будет иметь вид
Пусть в каждом ряду по точек. Способ соединить точки можно задать перестановкой
чисел,
первая точка
верхнего ряда соединяется с точкой под номером
вторая — с
и так далее. Значит, всего возможных рисунков будет
Теперь берём пару отрезков. Пусть это отрезки с концами и
считаем
В каком случае они пересекается? В том, когда
Учитывая, что
могут быть любой парой, замечаем следующее: общее количество пересечений отрезков равно количеству
случаев, когда в перестановке большее число стоит раньше меньшего (не обязательно по соседству). Как сказали бы старшие товарищи,
число пересечений равно числу инверсий в перестановке. Так и будем говорить дальше.
Например, — нет инверсий и нет пересечений,
— одна инверсия (
и
—
инверсий (
и
и
и
и
и
и
Наибольшее количество инверсий будет, если написать числа задом наперёд:
какие два числа не выбери — большее будет стоять раньше. То есть инверсий в последнем примере
а в общем случае —
Как посчитать число перестановок с заданным количеством инверсий? Подойдём к задаче индуктивно. В фигурных скобках будем
указывать различные перестановки, а в квадратных перечислим количества перестановок, имеющих соответственно
инверсий.
Итак, единственный элемент можно расположить единственным образом, и у нас есть одна перестановка с нулевым числом инверсий.
Добавляем двойку — её можно добавить в начало и в конец имеющейся перестановки Одна из полученных перестановок будет без
инверсий, другая — с одной инверсией.
Добавляем тройку — её мы можем поставить в любое место каждой из имеющихся перестановок. Тройка больше всех имевшихся ранее чисел, поэтому если поставить её на последнее место — новых инверсий не добавится, если поставить на предпоследнее (на второе) — добавится одна инверсия, а если на первое — будет плюс две инверии. Одна перестановка с нулём инверсий, две перестановки с одной, две перестановки с двумя, одна перестановка с тремя. То есть:
Так же будет происходить добавление нового числа в общем случае: число
можно поставить на любое место, и в зависимости от
места к инверсиям добавится
штук. То есть на новом шаге перестановка с
инверсиями превращается в
перестановок с
инверсиями соответственно.
Посмотрим, какие числа получались в квадратных скобках. Напишем эти последовательности одну под другой:
Здесь в строке (нумерация начинается с
) приводятся числа
для
равные количеству перестановок из
чисел с
инверсиями.
Вспоминая, как происходит добавление нового получим
Действительно, — количество перестановок из (n-1) чисел, в которых уже есть
инверсий. В них мы вынуждены поставить новое
на последнее место (
инверсий). Раз мы ставим
на единственно возможное место, количество перестановок не
изменится.
Далее, — количество перестановок с
инверсией, и, чтобы добавить недостающую, мы вынуждены ставить
на
предпоследнее место (
инверсия).
Продолжаем так вплоть до потому что добавить больше
инверсии нельзя. Всего получается
слагаемых. Из других
перестановок предыдущей строки мы ничего нового получить не сможем.
Заметим, что так как не бывает перестановок с отрицательным числом инверсий, как и не может быть перестановок со
слишком большим (больше чем
) количеством инверсий.
Итак, имеем следующий способ построения коллекции
Первая строчка:
По строчке ползёт «окно» шириной Попавшие в «окно» числа складываются и выписываются в следующую (2-ю)
строку:
Вторая строка:
По ней будет ползти окно шириной Сложение попавших в окно чисел даст третью строку:
По ней поползёт окно шириной и так далее, чтобы получить
строку, нужно складывать
стоящих подряд чисел предыдущей
строки.
Выпишем (без нулей) первые строк нашей коллекции и выберем в ней нужное нам
Получаем ответ
Ошибка.
Попробуйте повторить позже
На координатной плоскости дан параллелограмм с вершинами в точках ,
и
Найдите количество пар
точек
и
с целыми координатами, лежащих в этом параллелограмме (возможно, на границе) и таких, что
Источники:
Подсказка 1
Сначала может показаться, что задача какая-то жуть. Нужно находить количество пар точек, подходящие под какое-то странное условие... Но давайте понемногу "причёсывать" задачу и понимать, что от нас хотят. Попробуем хорошо преобразовать условие, данное на точки A и B. Какое действие хочется сделать, увидев в одной части координаты и точки A, и точки B?
Подсказка 2
Да, давайте перенесём координаты A в правую часть, а точки B — в левую. Число 33 тоже перенесём влево. Так как координаты у нас целые, то слева и справа получаются тоже какие-то целые значения. Пусть это будет целое число k. Что же теперь означает наше условие на координаты после того, как мы переписали их в удобном виде?
Подсказка 3
Верно, это две параллельные прямые, где вместо x и y мы подставляем координаты точек A и B. То есть мы можем записать уравнение прямых в общем виде с k. Что же нам теперь нужно сделать? Не забудем, что у нас есть ограничение на прямые самой границей параллелограмма. Идейная часть закончилась, теперь уже можно реализовывать техническую часть решения. Вспоминая вопрос задачи, что нам нужно теперь найти?
Подсказка 4
Верно, нам нужно найти в принципе количество целых точек x на прямых вида y=-3x+b. Это с помощью рассмотрения случаев, когда b делится на 3 и не делится, решается несложно(учитывая, конечно, снова ограничение по параллелограмму). Найдя уже до этого ограничения на k, остаётся только дело за комбинаторикой. То есть нам нужно для каждого k, выбрать на прямых нужные нам целые точки.
Запишем исходное условие на координаты точек и
в виде
Так как координаты точек и
являются целыми числами, то левая и правая части этого равенства могут принимать только целочисленные значения
Пара точек
и
с целочисленными координатами удовлетворяет условию тогда и только тогда, когда они лежат на
параллельных прямых
соответственно. Найдём подходящие значения параметра
Стороны и
параллелограмма лежат на прямых
поэтому они параллельны прямым, на которых лежат точки и
Эти прямые пересекают параллелограмм
при
|
|
Выясним количество точек с целочисленными координатами на каждой из прямых вида
Рассмотрим несколько вариантов:
Если
кратно трём (т.е.
то получаем прямую
При любом целом получится целое значение
а чтобы точка оказалась в параллелограмме нужно, чтобы
При любом этому неравенству удовлетворяет
целых значений
Если
не делится на 3, т.е. при
где
имеем
Учитывая, что получаем
Значит, этому неравенству удовлетворяет целочисленных значений.
Если (таких значений
то на каждой из двух прямых
можно выбрать по точек — всего
пар.
Если (таких значений
то на каждой из двух прямых можно выбрать по
точек — имеем
пар.
Итого получаем
Ошибка.
Попробуйте повторить позже
На плоскости отмечено 9 различных точек, среди которых есть красные, синие и зеленые. Точек других цветов нет. Известно, что сумма всех попарных расстояний между красными и синими точками равна 13, между красными и зелеными равна 11, а между синими и зелеными равна 1. Каким может быть количество красных отмеченных точек?
Источники:
Подсказка 1
Пупупу…давайте подумаем, а что можно сказать про тройку из трех точек различных цветов?
Подсказка 2
Верно, для каждой такой тройки выполняется неравенство треугольника!(убедитесь, что если точки лежат на одной прямой, то это неравенство тоже выполняется) Так, но это условие мы получили только для одной конкретной тройки точек, а можно ли получить что-то про все точки сразу?
Подсказка 3
Да, можно сказать, что сумма всех расстояний между красными и синими точками не больше чем сумма суммы расстояний между красными и зелеными точками и суммы расстояний между синими и зелеными! А как это записать математически?
Подсказка 4
Конечно, иными словами: 13r ≤ 11q + p, где r- количество красных точек, q – синих точек, p – зеленых точек! Аналогично можно сказать, что 11q ≤ 13r+p(опять же в силу неравенства треугольника) А также не забываем про условие, что p+q+r=9. Осталось найти возможные значения p, q, r и привести пример, что каждый случай достигается!
Пусть отмечены красные точки , синие точки
, и зеленые точки
.
Поскольку для каждой точки выполняется неравенство треугольника
, то
Откуда .
Аналогично, просуммировав неравенства , получим
.
Далее перебором можно установить, что найденным соотношениям и равенству удовлетворяют ровно две тройки
натуральных чисел
Покажем, что оба найденных варианта могут быть реализованы на прямой. Каждую из отмеченных точек будем задавать ее координатой.
Первый вариант:
Второй вариант: .
5 или 7



