Рассмотрим все кружки размера Никакие два из этих множеств не пересекаются по двум элементам. В каждом множестве пар элементов, а всего пар элементов Значит, всего кружков размера не более Значит, всего множеств не более

что и требовалось доказать.

Будем называть не враждующих детей друзьями. Раз у каждого не больше врагов, то у каждого хотя бы друзей и из них хотя бы — не его одноклассники. Выберем пару из ученика и класса, в котором тот не учится, так, чтобы количество знакомых у этого ученика в выбранном классом было наибольшим (среди всех указанного вида). Назовем такого ученика Васей, пусть он учится в классе А, выбран класс Б, где у него друзей, а в В классе друзей, рассмотрим одного из них — Петю.

Отметим, что поскольку а в классах по учеников, то (и такой Петя найдется). Если условие не выполнено, то у Пети в Б классе не более (иначе вместе с Васей у них в этом классе есть общий друг). Значит, в А классе у Пети хотя бы друг, противоречие с выбором, который был ранее сделан.

Пойдём от противного, пусть не существует более клубов с одинаковым числом жителей. Рассмотрим клуб с наибольшим количеством жителей, пусть в нём человек. Кроме этого клуба эти люди входят ещё в хотя бы клубов, поскольку каждый входит в хотя бы клубов и клубы пересекаются не более чем по одному человеку. Тогда всего получается хотя бы клуб, включая самый большой. Заметим, что по принципу Дирихле найдётся хотя бы клубов с одним количеством жителей, потому что всего не более различных размеров клубов, что и требовалось.

Возьмём произвольное слово длины 20 и будем последовательно передвигать в нем буквы A, не уменьшая при этом крутизну слова. Ясно, что в нашем слове должно быть хотя бы две буквы B, иначе крутизна слова равна 0. Далее, предположим, что в слове между двумя буквами В есть буква А, т.е. слово имеет вид ... В. .. А. .. В ... Посмотрим, с какой стороны от буквы А больше букв А, и передвинем выделенную букву А в тот конец слова, где их меньше. Заметим, что при таком перемещении буквы А мы могли разрушить лишь слова вида ABBA и ABBA, которые давали вклад в размер крутизны исходного слова. Предположим, что мы переместили букву К налево. Тогда слова вида ABBA сохранились, а вместо слов вида ABBA, образованных буквой В слева от и двух букв В и буквы , мы получим как минимум столько же слов, которые образуются из нашей передвинутой буквы , двух любых букв У и любой буквы А, которая стояла в исходном слове справа от буквы А. Получается, что мы можем рассматривать только слова вида А...АВ...ВА...А. Если в левом блоке будет букв А, а в правом букв А, то крутизна такого слова равна .

Заметим, что при фиксированной сумме произведение будет максимальным, если числа и отличаются не больше чем на 1: в противном случае, если, например, , то переместим одну букву из левого блока в правый, и крутизна изменится на

Таким образом, можно считать, что или , причем (иначе в нашем слове не будет или букв А, или букв В). Теперь возьмем слово, в котором , и заменим последнюю букву В на букву А. При такой замене крутизна слова изменится на величину

Значит, при крутизна слова после такой замены увеличивается, а при уменьшается. Аналогично, посмотрим, что произойдёт, если в слове, в котором , заменить первую букву В на букву A:

Получается, что при крутизна слова после такой замены увеличивается, а при - уменьшается. Значит, мы можем последовательно совершать такие замены, сводя величину к значению 5 и увеличивая в процессе крутизну. В итоге, наибольшая крутизна будет у слова, в котором , и равна она .

Замечание.

Последнюю часть решения можно провести по-другому. А именно, рассмотрим крутизну слова, в котором , как функцию от . Вычислим ее производную: . Нас интересует натуральная точка из отрезка , которая наиболее близка к нулю этой производной. Поскольку , в качестве такой точки необходимо выбрать число , что и приводит нас к примеру. Аналогичные вычисления для случая также дают значение , но крутизна такого слова оказывается меньше.

Оценка.

Можно считать, что первый наклеенный кусок — весь квадрат, от этого ничего не испортится. Считаем его нулевым. Докажем индукцией по утверждение:

_________________________________________________________________________________________________________________________________________________________________________________

После еще кусков между любыми двумя клетками есть путь с не более чем сменами цвета.

_________________________________________________________________________________________________________________________________________________________________________________

База при верна.

_________________________________________________________________________________________________________________________________________________________________________________

Рассмотрим наклеивание -го куска . Пусть до этого между двумя клетками был путь с не более сменами цвета. Если он не заходил в , то он таким и остался. Иначе заменим его кусок от первой его клетки в до последней такой клетки на путь по между этими клетками. Тогда количество смен цвета в новом пути увеличилось не более чем на 2 по сравнению со старым. Переход доказан.

_________________________________________________________________________________________________________________________________________________________________________________

В конце между противоположными углами любой путь имеет хотя бы 88 смен цвета. Значит, поверх нулевого куска наклеено еще хотя бы 44.

_________________________________________________________________________________________________________________________________________________________________________________

Пример.

Пусть верхний слой состоит из центральной клетки. Далее пусть каждый нижележащий слой состоит из клеток предыдущего слоя и из клеток, примыкающих к ним по стороне, и имеет противоположный цвет.

Первое решение.

Рассмотрим всевозможные мелодии из нот до и си длины , коих штук. Каждую такую мелодию периодически продолжим в обе стороны, получив бесконечную в обе сторону мелодию. Назовём две получившиеся бесконечные мелодии эквивалентными, если одна получается из другой сдвигом.

Наименьший период всех бесконечных мелодий, кроме двух, состоящих только из нот до и только из нот си, равен Количество не эквивалентных друг другу бесконечных мелодий равно

(каждой бесконечной мелодии периода эквиваленты мелодий (включая саму с периодом, который будет циклическим сдвигом нот, дающих мелодию )

Из них мелодий, содержащих запрещённые Кощеем мелодии, не больше

(в скобках учтены запретные мелодии длины , полученные дописыванием символов к запретной мелодии длины , а за скобками — все остальные).

Таким образом, найдётся бесконечная мелодия, которая не содержит запретных мелодий, и для прохождения испытания Ивану достаточно сыграть её кусок длины

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть - число мелодий длины , не содержащих запретных последовательностей нот. Будем считать, что По индукции докажем, что для всех натуральных .

База индукции

Предположим, что неравенство верно для всех , меньших Покажем, что тогда Заметим, что

Действительно, мы можем добавить в конец ноту двумя способами к уже имеющейся незапрещенной мелодии из нот. При добавлении ноты могла возникнуть запретная мелодия длины в конце последовательности, однако она "испортит"максимум последовательности нот, так как первые ноты до "запрещенной"мелодии - незапрещенная мелодия длины . Аналогично могли получить запретную последовательность из нот и испортить разрешённую мелодию из нот и т. д. (Здесь мы можем вычесть лишнее, если , и часть вычитаемых мелодий могут быть одинаковыми, но поскольку мы пишем оценку снизу, всё правильно.)

Из предположения индукции для также следуют неравенства:

Применим эти следствия, а также неравенство выше, для доказательства перехода индукции и получим:

Следовательно, и переход доказан.

Тогда из-за положительности последовательность возрастающая, а значит , откуда следует, что Иван справится с испытанием Кощея.

Расположим наши числа по убыванию, Имеем

Умножим первое равенство на получим, что

Следовательно,

Первое решение. Индукцией покажем, что для городов База очевидна.

Шаг индукции. Пусть для городов стёрто не более записей. Выберем город для которого стёрто хотя бы одно расстояние до другого города, и рассмотрим остальные городов. Между ними стёрто не более расстояний, и по предположению индукции можно восстановить все эти расстояния, а тогда и взаимное расположение этих городов на плоскости. Для города известны расстояния по крайней мере до трёх городов, и это позволяет однозначно восстановить его расположение. Увеличить до нельзя. Пусть неизвестны расстояния от точки до всех точек, кроме и Тогда положение точки определено с точностью до симметрии относительно прямой значит, расстояния от неё до остальных точек не восстанавливаются.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение. Рассмотрим граф со вершинами и рёбрами, соответствующими стёртым записям. Этот граф содержит не менее четырёх компонент связности. Зафиксируем по вершине ) в каждой из этих четырёх компонент. Все расстояния между этими вершинами известны. Рассмотрим произвольную вершину первой компоненты. Известны её расстояния до точек следовательно, положение соответствующего города на плоскости определено однозначно. Аналогична ситуация с вершинами оставшихся компонент.

Турнир задается выбором ориентации ребер, которых . Поэтому всего турниров . Рассмотрим вероятностное пространство, элементами которого будут все турниры на вершинах, причем для различных ребер их ориентации независимы. Это означает, что все турниры равновероятны.

Для каждой из ! перестановок вершин рассмотрим случайную величину , равную единице, если вершины турнира образуют гамильтонов путь именно в этом порядке и 0 в противном случае.

Математическое ожидание равно вероятности того, что она равна 1 , т.е. , как произведение вероятностей независимых событий с вероятностью каждое.

Число гамильтоновых путей в случайном турнире - тоже случайная величина, равная сумме по всем возможным перестановкам , поэтому его математическое ожидание в ! раз больше, т.е. равно . С другой стороны, математическое ожидаение в данном случае - среднее значение числа гамильтоновых путей в турнире, поэтому существуют турниры, в которых не меньше гамильтоновых путей.

Покажем стратегию игры за Федора. Без ограничений общности считаем, что изначально фишка находится в верхнем левом углу. Первым ходом передвинем фишку в левый нижний угол. Каждым следующим ходом будем сдвигать фишку на наибольшее возможное число клеток вверх или вниз, пока это возможно.

После каждого хода будет удалять все клетки, в которых фишка уже находилась или не сможет оказаться при любой игре.

Индукцией по количеству ходов Федора покажем, что после каждого его хода доска является прямоугольником при этом следующих ход будет совершен Сергеем в одну из угловых клеток.

База индукции верна, поскольку после первого хода доска имеет вид прямоугольника причем следующих ход будет совершен Сергеем в нижнюю левую клетку.

Докажем переход. Пусть после некоторого хода Федора доска имеет вид причем Сергей совершит ход в одну из угловых клеток и делает несколько ходов по горизонтали, после чего из этой клетки Федор вновь совершает максимальное количество ходов по вертикали. После этого хода Сергей может сделать ход либо вправо, либо влево. Если в каждой из этих случаев доска будет иметь вид то Федор сделает последний ход и победит. Иначе одном из случаев доска будет иметь вид прямоугольника в другом причем если и а значит и что доказывает переход

Заметим, что каждая пара ходов Федора и Сергея уменьшает сумму количества столбцов и строк доски по крайней мере на 1, а значит не позже, чем через ходов, доска придет к виду где Следующим ходом Сергей встанет на самую верхнюю или нижнюю клетку доски, после чего Федор пройдется по всем оставшемся ее клеткам и завершит игру.

Отсортируем числа из множества по возрастанию:

Для любых трех последовательных чисел число по условию лежит в . Но

Тогда это число должно равняться , откуда . В силу произвольности выбора номера получаем, что каждое число является средним арифметическим двух его соседей, но тогда это арифметическая прогрессия.

По условию числа , то есть , где - разность прогрессии.

и в силу того, что , а натуральное. Имеем единственное решение .

Заметим, что если машинка может проехать из клетки в клетку то она может проехать из клетки в клетку — проезжая тот же маршрут в обратном порядке. Поэтому достаточно доказать, что, выезжая из дома, машинка может выехать за границу квадрата.

Пусть знаки как-то расставлены. «Выпустим» машинку из дома. Пусть она движется согласно "правилам дорожного движения поворачивая попеременно то вправо, то влево. Тогда она не может "зациклиться"и когда-то выйдет за пределы квадрата

На каждом шаге Петя уменьшает произведение чисел на доске на число, которое он пишет на бумажке: поэтому произведение чисел на доске сложенное с суммой чисел на бумажке не изменяется. Поскольку в конце произведение на доске будет равно сумма на бумажке равна исходному произведению

Ясно, что у каждого есть одинаковое количество друзей, обозначим его через Рассмотрим ребёнка и его друзей.

Ясно, что эти человек попарно дружат между собой и враждуют со всеми остальными. Удалим из кружка и его друзей. Найдём в среди оставшихся человека и его друзей и также их удалим. Продолжая этот процесс далее, замечаем, что если в компании есть хотя бы один человек, то в ней есть компания из друзей, которую мы можем удалить. Значит, процесс закончится тогда, когда мы удалим всех детей из кружка. Отсюда заключаем, что кратно (пусть ).

Теперь рассмотрим любого ребёнка. Он состоит в одной из компаний друзей, а с ребятами из остальных компаний враждует. Значит, у него врагов. Это уравнение имеет решения

Этим решениям соответствуют и Примеры строятся в соответствии с решением: групп по ребят. Внутри групп ребята дружат, а ребята из разных групп враждуют.

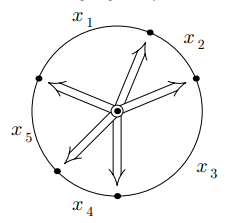
Отметим на одном циферблате положения часовых стрелок всех часов. Циферблат разобьется на секторов. Занумеруем их по кругу. Пусть часовая стрелка проходит секторы за время соответственно (некоторые из этих чисел, возможно, нулевые). Заметим, что если мы станем устанавливать на всех часах время, соответствующее положению внутри сектора, то каждая часовая стрелка пройдет через начало сектора. Это значит, что суммарное время перевода окажется заведомо больше, чем если бы мы устанавливали все часы на начало сектора. Обозначим через суммарное время, необходимое для установки всех часов на начало -го сектора. Ясно, что время перевода отдельной стрелки является суммой некоторых Например, время перевода на начало первого сектора равно для пятых часов и для вторых. Тогда

Остальные выражаются аналогично. Тогда часов.

Поэтому наименьшая сумма не превосходит часа. С другой стороны, если все секторы одинаковы (например, часы показывают ч, ч мин, ч мин, ч мин и ч мин), то все равны часам, поэтому менее, чем часами не обойтись.

Среди пяти чисел в сумме точно есть одно чётное, так как если все числа нечётные, то и их сумма нечётная, а чётное. Значит, есть одно чётное число, а нечётное. Такого быть не может.

Из первого условия следует, что ровно у точек оба соседа белые, а из второго — что ровно у точек оба соседа черные. Это означает, что у оставшихся точек соседи разного цвета.

Посчитаем всех белых соседей: раз считаются белые соседи, при этом каждая точка учитывается дважды, так как у нее два соседа. Значит, белых точек

Комментарий. Так как в условии сказано, что данная ситуация случилась, и у нас получился единственный ответ, приводить пример на это количество не нужно.

Пусть такие числа существуют. Так как все числа различные, то давайте упорядочим их по убыванию Теперь давайте посмотрим на суммы с самым наибольшим числом и аналогично упорядочим по убыванию Частные, которые будут получаться при делении суммы всех чисел на эти, как минимум, могут быть от до Но слишком большое число, и равенства не будет. Противоречие.

Сопоставим каждому числу в таблице пару весов где  — количество таких же чисел в одной строке с выбранным (включая его), а  — количество таких же чисел в одном столбце с ним. Назовем полным весом числа из таблицы сумму двух его весов. Для каждого оценим снизу сумму полных весов чисел, равных Пусть такие числа входят в строк и столбцов. Заметим, что тогда числа, равные могут стоять только в пересечении таких строк и столбцов, откуда Заметим, что в каждой строке из сумма первых весов чисел, равных равна Аналогично со вторыми весами и столбцами. Тогда вся сумма полных весов равна

Если теперь просуммировать полученные неравенства по всем то получим, что сумма полных весов всех чисел в таблице не меньше По принципу Дирихле либо сумма первых весов не меньше либо сумма вторых весов не меньше Не нарушая общности, пусть верно первое предположение. Тогда в какой-то строчке сумма первых весов чисел не меньше Но с другой стороны легко видеть, что сумма первых весов одной строчки равно количеству различных чисел в этой строчке, то есть в найденной строке не менее различных чисел.

Отметим все стрелок на одном циферблате. Заметим, что минимальное время будет заведомо достигаться в начальном положении одной из стрелок (если мы все стрелки сдвинули по часовой стрелке, то можно уменьшить время перевода на часов, уменьшив время перевода для каждой стрелки на час).

Наши шесть стрелок разбили циферблат на 6 секторов. Пронумеруем наши стрелки числами от до и обозначим через размер сектора, идущего после -ой стрелки (в часах). Если все стрелки мы перевели в положение то первую стрелку мы не переводили, вторую мы перевели на часов, …, шествую перевели на часов. Тогда суммарное время перевода в этом случае будет равно

Если мы проделаем аналогичные рассуждения для других пяти положений а потом сложим, то в сумме получится

Тогда для какого-то из положений сумма будет не больше, чем часов. То есть можно выбрать такое положение, что суммарное время перевода будет не больше, чем часов.

Осталось привести пример, показывающий, что эта оценка достигается. Можно поставить стрелки через каждые часа (то есть первые часы на часов, вторые — на часа, …, шестые — на часов). Из нашей оценки минимальное время перевода будет в одном из этих положений. Но легко видеть, что в каждом положении суммарное время перевода действительно равно часам.