Ошибка.
Попробуйте повторить позже
Таблица заполняется по правилам игры “Сапёр
”: в некоторые клетки ставится по одной мине, а в каждой из остальных клеток
пишется количество мин во всех примыкающих к ней по стороне клетках. Какое наибольшее значение может принимать сумма всех
записанных чисел?
Пример. Черные клетки шахматной раскраски сделаем минами, а белые оставим пустыми.
Оценка. Клетки без мин будем называть пустыми. Покрасим внутренние ребра нашей таблицы: если ребро разделяет мину и пустую
клетку, покрасим ее в синий цвет, а иначе — в красный. Заметим, что в пустой клетке написано количество синих рёбер, прилегающих к ней,
а также то, что синее ребро прилегает ровно к одной пустой клетке. Отсюда следует, что сумма чисел в таблице равна количеству синих
ребер, а их в свою очередь не больше, чем ребер всего
Ошибка.
Попробуйте повторить позже
Дана клетчатая доска Клетки доски покрашены в
цвета так, что в каждой строке и в каждом столбце ровно
клеток
каждого цвета. Докажите, что найдутся
строки и
столбца, клетки на пересечении которых окрашены в
различных
цвета.
Предположим противное: пусть среди четырёх клеток на пересечении любых двух строк и любых двух столбцов есть две клетки одинакового цвета.
Назовём горизонтальной (вертикальной) парой две клетки разного цвета, лежащие в одной строке (одном столбце). Назовём
горизонтальным (вертикальным) совпадением две клетки одинакового цвета, лежащие в одной строке (одном столбце). Разделим пары на 6
типов по цветам входящих в них клеток:
Рассмотрим две произвольные строчки. Из предположения следует, что каждые две вертикальных пары с клетками в этих
строчках должны иметь общий цвет. Тогда в двух рассматриваемых строчках могут быть вертикальные пары не более,
чем трех типов, причем возможны только два принципиально различных случая: все пары содержат один и тот же цвет
(скажем, ) или есть пары типов
и
(или точно так же с другой тройкой цветов). Рассмотрим эти два
случая.
Если все пары в наших двух строчках содержат клетку цвета то всего пар не более, чем клеток цвета
в обеих строчках, то есть не
более
Значит, в рассматриваемых двух строчках не менее
совпадений.
Пусть есть пары типов и
В этом случае все клетки цвета
в наших строчках совпадают, таким образом, есть не
менее
совпадений.
Итак, мы доказали, что в каждой паре строчек не менее вертикальных совпадений. Аналогичный результат верен и для любой пары
столбцов. Таким образом, всего в нашем квадрате есть не менее
совпадений. Но так как в каждой строке и в каждом столбце по
клеток каждого цвета, количество совпадений равно
Учитывая, что
приходим к
противоречию.
Ошибка.
Попробуйте повторить позже
На клетчатой бумаге по границам клеток обведен квадрат Он покрыт
квадратами
каждый закрывает в точности
клетки. Докажите, что можно убрать один из квадратов так, что оставшиеся будут по-прежнему покрывать весь квадрат
Верхней-левой клеткой любого квадрата может быть только одна из
клеток верхнего-левого квадрата
Разобьём эти
клетки на
полосок
Так как
то по принципу Дирихле в некоторую полоску попадут верхне-левые клетки не менее чем
трёх квадратов. Если среди этих трёх квадратов есть совпадающие — можно убрать один из совпадающих. Если нет — можно убрать
средний, так как он покрыт двумя крайними.
Ошибка.
Попробуйте повторить позже
Таблица состоит из строк и
столбцов. В каждой клетке таблицы написана цифра. Известно, что для каждой строки
и
каждой пары столбцов
и
существует строка, отличающаяся от
в точности в столбцах
и
Докажите, что
Пусть — первая строка таблицы. Рассмотрим любой набор из чётного количества столбцов и пронумеруем их слева направо:
Тогда в таблице есть строка
отличающаяся от
ровно в столбцах
и
далее, есть строка
отличающаяся
от
ровно в столбцах
и
и так далее; наконец, есть строка
отличающаяся от
ровно в столбцах
и
(если
то
). Итак, строка
отличается от
ровно в столбцах
Значит, строки
построенные по
различным наборам столбцов, различны. Поскольку количество наборов из чётного числа столбцов равно
то и количество строк в
таблице не меньше
Ошибка.
Попробуйте повторить позже
В каждой клетке таблицы записано число. Назовём клетку хорошей, если сумма чисел строки, содержащей эту
клетку, не меньше, чем сумма чисел столбца, содержащего эту клетку. Найдите наименьшее возможное количество хороших
клеток.
Источники:
Подсказка 1
Попробуем воспользоваться стандартным приемом при решении задач с досками — а что если разбить доску на удобные нам группы клеток, в которых мы сможем оценить количество хороших?
Подсказка 2
Так как мы минимизируем количество хороших, то нам нужны такие группы, в каждой из которых будет хотя бы одна хорошая.
Подсказка 3
То есть нужны группы, в которых все клетки не могут быть плохими. А что будет, если все клетки будут плохими? Как это переформулировать?
Подсказка 4
Нужны такие клетки, чтобы у нас уж точно сумма по столбцам была не больше, чем сумма по строкам
Подсказка 5
А что если сделать так, чтобы эти столбцы и строки образовывали всю доску?
Оценка.
Разобьём все клетки таблицы на грушп по
клеток так, чтобы в каждой груше все клетки находились в разных строках и разных
столбцах. Пример такого разбиения для
см. на рисунке:
| 1 | 2 | 3 | 4 | 5 |
| 5 | 1 | 2 | 3 | 4 |
| 4 | 5 | 1 | 2 | 3 |
| 3 | 4 | 5 | 1 | 2 |
| 2 | 3 | 4 | 5 | 1 |
Для других разбиение аналогично: например, в одну группу берём главную диагональ (идущую сверху слева вниз вправо), во вторую
— диагональ над ней и число в левом нижнем углу, в третью — следующую диагональ и диагональ из двух клеток слева внизу, и
т.д.
Предположим, что в какой-то группе все клетки плохие. Тогда для каждой клетки этой группы сумма чисел содержащей её строки
меньше суммы чисел содержащего её столбца. Суммируя эти неравенства по всем клеткам групшы, получаем, что сумма чисел во всей
таблице, подсчитанная по строкам, меньше, чем эта же сумма, подсчитанная по столбцам - противоречие, Значит, в каждой группе есть
хорошая клетка, и число хороших клеток не меньше числа групп, то есть не меньше .
_________________________________________________________________________________________________________________________________________________________________________________
Пример, подтверждающий точность полученной оценки
хороших клеток уже возможно.
Пусть в первой строке стоят единицы, а в остальных нули. Тогда все клетки первой строки хорошие, а остальные плохие.
Ошибка.
Попробуйте повторить позже
Петя и Вася независимо друг от друга разбивают белую клетчатую доску на произвольные группы клеток, каждая из чётного (но
не обязательно все из одинакового) числа клеток, каждый - на свой набор групп. Верно ли, что после этого всегда можно покрасить по
половине клеток в каждой группе из разбиения Пети в чёрный цвет так, чтобы в каждой группе из разбиения Васи было поровну чёрных и
белых клеток?
Первое решение.
Заметим, что частным случаем разбиений является ситуация, когда каждая из Петиных и Васиных групп содержит в точности две клетки. С другой стороны, любое разбиение на группы из четного числа клеток можно измельчить на группы из двух клеток, и если существует требуемая раскраска для измельченных разбиений, то та же самая раскраска, очевидно, решает задачу и для исходных разбиений.
Теперь каждую Васину группу (из двух клеток), совпадающую с какой-то из Петиных групп, покрасим в черный и белый цвет любым из двух способов - одну клетку в черный, другую в белый цвет.
Осталось раскрасить множество клеток, которое Васей и Петей разбито на пары так что ни одна Васина пара не совпадает с Петиной парой.
Построим граф, вершины которого соответствуют Васиным и Петиным группам (у Васи и Пети, очевидно, одно и то же количество групп). Две вершины соединим ребром тогда и только тогда, когда соответствующие группы имеют общую клетку. Тогда каждая вершина графа имеет степень два, причем любое ребро соединяет одну из вершин, соответствующих Васиным группам, с одной из вершин, соответствующих Петиным группам.
Такой граф разбивается на циклы, причем каждый цикл имеет четную длину (за счет того, что в нем чередуются вершины, соответствующие Васиным и Петиным групам) и допускает раскраску в два цвета, при которой цвета ребер чередуются вдоль цикла. Наконец, цвету клетки сопоставим цвет ребра, соединяющего две вершины графы, соответствующие Васиной и Петиной группам, пересекающимся по данной клетке. Полученная раскраска удовлетворяет условию задачи.
_________________________________________________________________________________________________________________________________________________________________________________
Второе решение.
Для удобства назовём непересекающиеся группы клеток одного разбиения (Пети или Васи) фигурками.
Построим вспомогательный двудольный граф G. Для каждой из фигурок одного из разбиений (Пети или Васи) добавим в граф
новую, соответствующую этой фигурке вершину. При этом вершины, соответствующие фигуркам Пети, отнесём к первой доле, а вершины,
соответствующие фигуркам Васи, - ко второй. Далее проведём рёбра между некоторыми вершинами графа
по следующему правилу: если
фигурка Пети
пересекается с фигуркой Васи
по нечётному количеству клеток, то проведём между соответствующими этим
фигуркам вершинами ребро.
Заметим, что в построенном графе степень каждой вершины чётна. Действительно, выберем, например, произвольную фигурку Васи .
Поскольку
состоит из чётного числа клеток и пересекается лишь с фигурками из разбиения Пети, то по нечётному количеству клеток
она будет пересекаться с чётным количеством фигурок.
Рассмотрим произвольную компоненту связности . Поскольку степень каждой вершины этой компоненты чётна,
то существует цикл (т.н. эйлеров цикл), проходящий по всем рёбрам этой компоненты ровно по 1 разу. Выберем такие
циклы для каждой компоненты связности
. Для удобства назовём полученное разбиение рёбер графа
на циклы
.
Теперь построим искомую раскраску фигурок в разбиении Пети. Выберем произвольный цикл из построенного разбиения
и
ориентируем его рёбра в каком-то из двух возможных естественных направлений его обхода. Рассмотрим произвольное (уже
ориентированное) ребро
цикла
. Пусть оно соединяет вершины, соответствующие фигуркам
и
. По построению фигурки
и
пересекаются по нечётному количеству клеток. Пусть они пересекаются по
клетке. Тогда если ребро
ведёт из первой доли во
вторую, то Петя покрасит произвольные
из них в чёрный цвет и произвольные
из них в противном случае. Пусть Петя
выполнит аналогичную покраску для каждой компоненты связности
. Наконец, пусть для каждой пары фигурок
и
, пересекающихся по чётному количеству клеток, Петя покрасит ровно половину клеток в их пересечении в чёрный
цвет.
Докажем, что полученная покраска будет искомой. Рассмотрим, например, произвольную фигурку Пети . Пусть
- произвольная
фигурка Васи. Заметим, что среди общих клеток фигурок
и
разность числа чёрных и белых клеток равна
или 0 , в зависимости
от чётности числа клеток в этом пересечении. Поэтому достаточно доказать, что разность +1 встречается среди пересечений фигурки Пети
с фигурками Васи столько же раз, сколько и разность -1 . Пусть фигурке
в графе
соответствует вершина
,
которая лежит в некотором цикле
из построенного ранее разбиения
. Тогда каждой разности +1 соответствует ребро
цикла
, входящее в
, а каждой разности -1 - ребро цикла
, исходящее из
. Из построения цикла
следует,
что рёбер, входящих в
, в нём будет столько же, сколько и рёбер, исходящих из
. Поэтому фигурок Васи, в клетках
пересечения
с которыми будет ровно на одну чёрную клетку больше, будет столько же, сколько фигурок Васи, в клетках
пересечения
с которыми будет ровно на одну белую клетку больше. Таким образом, в фигурке
поровну чёрных и белых
клеток.
Ошибка.
Попробуйте повторить позже
Можно ли в таблице расставить числа
,
и
так, чтобы все суммы чисел по вертикалям, горизонталям и двум главным
диагоналям были различны?
В условии требуется, чтобы значения сумм (
строк,
столбцов и две диагонали) были различны. Каждая из этих сумм состоит
из
слагаемых, принимающих одно из значений
,
,
. Поэтому каждая из сумм принимает целочисленное значение в диапазоне от
до
. Всего возможных значений сумм —
. Поскольку
, какие-то две из сумм обязательно принимают
равные значения.
Ошибка.
Попробуйте повторить позже
Можно ли отметить некоторые клетки квадрата так, чтобы в любом прямоугольнике из
клеток было нечётное число
отмеченных?

Нужно разбить плоскость на квадраты и раскрасить каждый квадрат как показано на рисунке. Заметим, что условие достаточно
проверять только для прямоугольников площади
так как любой прямоугольник площади
разбивается на нечетное число таких
прямоугольников. А раскраска
как раз подбирается так, чтобы в любом прямоугольнике площади
было нечетное число
клеток.
Да
Ошибка.
Попробуйте повторить позже
Из квадрата удалили центральную клетку, оставшуюся часть разбили на доминошки из двух клеток. Мальчик Витя не видит
разбиение, но он может разместить на доске прямоугольник из
клеток и узнать, сколько доминошек содержат хотя бы одну клетку в
данном прямоугольнике (прямоугольник из
клеток не должен вылазить за пределы квадрата, но может содержать удалённую клетку).
Такую операцию он может проделывать несколько раз. Какое наибольшее количество доминошек Витя сможет гарантированно
восстановить, вне зависимости от разбиения на доминошки?
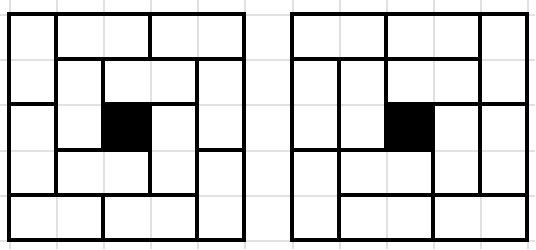
Заметим, что в разбиениях как на рисунке выше в каждом прямоугольнике из клеток лежат клетки одинакового числа
доминошек, при этом совпадающих доминошек ровно
Значит, Витя может гарантированно определить не более
доминошек.
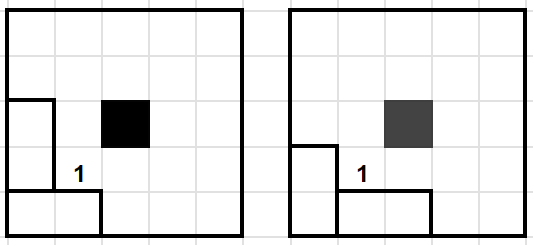
Покажем, что Витя всегда сможет восстановить положение хотя бы доминошек. Выберем угол квадрата и узнаем, сколько доминошек
в каждом из
прямоугольниках, примыкающих к углу. В одном из них точно будет
доминошки. Если в другом их
то мы знаем
расположение доминошки, примыкающей к углу. Иначе мы понимаем, что у нас одна из ситуаций как на рисунке выше. Тогда спросим про
два прямоугольника с центром в клетке
На ровно один из вопросов мы получим ответ
а на другой —
Тогда в том
прямоугольнике, для которого ответ —
лежит целая доминошка с клеткой
Таким образом, «около» каждого из углов
мы умеем определять расположение одной из доминошек. Значит, всего мы сможем определить положение хотя бы
доминошек.
Ошибка.
Попробуйте повторить позже
Таблица заполнена числами как показано на рисунке:
| 1 | 2 | 3 | … | 100 |
| 101 | 102 | 103 | … | 200 |
| | | | | |
| 9901 | 9902 | 9903 | … | 10000 |
Можно ли переставить некоторые числа так, чтобы в каждой клетке по прежнему стояло одно число, и чтобы во всех прямоугольниках из трех клеток сумма чисел не изменилась?
Подсказка 1
Часто задачи с таблицами решаются раскрасками. А какая раскраска имеет какие-то приятные свойства для прямоугольников из трех клеток?
Рассмотрим раскраску таблицы в три цвета, как показано на рисунке:
| 1 | 2 | 3 | … | 1 |
| 2 | 3 | 1 | … | 2 |
| 3 | 1 | 2 | … | 3 |
| | | | | |
| 1 | 2 | 3 | … | 1 |
Если в исходной таблице к числам цвета 2 прибавить единицу, а из чисел цвета 3 вычесть единицу, то мы получим такую перестановку, что набор чисел сохранится. А сумма в каждой тройке тоже.
Ошибка.
Попробуйте повторить позже
У вредного Васи есть клетчатая полоска длины 13 клеток и лента длины клеток, каждая шириной в одну клетку. Вася хочет
разрезать полоску на кусочки произвольной длины из нескольких целых клеток по своему усмотрению, а затем уложить часть из них на
ленту в некотором порядке так, чтобы в какой-то момент осталось не менее одного кусочка, ни один из которых уложить уже нельзя. При
этом кусочки укладываются строго по клеткам и не могут выходить за пределы ленты, ни одна клетка не должна быть накрыта ими
дважды и, если на ленте есть место, куда можно уложить очередной кусочек, Вася должен уложить его в одно из таких мест по своему
выбору. При каком минимальном N, как бы Вася ни старался, ему не удастся задуманное, то есть придётся уложить все
кусочки?
Источники:
Подсказка 1
Давайте попробуем себе немножко упростить задачу и посмотреть на финальный шаг, когда Вася не может уложить ни один из своих кусков, можно ли как-то без ограничения общности заменить их?
Подсказка 2
Да, давайте скажем, что в конце у Васи остался ровно 1 кусок длины x, и он положил до этого k отрезков. Давайте тогда попробуем как-то оценить N, интуитивно должно казаться, что длина каждого из k кусочков должна быть как можно меньше, и они должны выступать в качестве ограничителей для нашего кусочка x.
Подсказка 3
Если всё ещё не получается получить оценку, то не расстраивайтесь и подумайте, какое наибольшее расстояние может быть между двумя соседними кусочками, чтобы между ними не поместился кусок x, а сколько таких промежутков, куда можно в теории положить x (не забудьте, что лента по краям тоже ограничена), а также не забудьте про сами k кусочков, они тоже занимают место на ленте.
Подсказка 4
Мы получили, что N ≤ (x-1)(k+1) + (13-x) ≤ 48, остаётся только придумать пример, когда N=48 (потому что для меньших свойство о непокрываемости), и радоваться решённой задаче!
Заметим, что если в какой-то ход Васи осталось больше одного кусочка, а оставшиеся поместить нельзя, то можно рассмотреть разрезание, где все эти кусочки объединяются в один, а другие выкладываются на ленту тем же образом. Понятно, что такой кусок-склейка также не будет помещаться.
Значит, можно без ограничения общности предположить, что у Васи должен остаться ровно один кусок, который нельзя
поместить. Пусть его длина , а количество положенных кусочков равно
. Тогда
, при этом длина полосы
, так как
- количество клеточек занятых остальными кусочками, а
- количество ’зазоров’, в
которые теоретически мы могли поместить кусок длины
, но он не поместился, так как размеры зазоров не превосходят
.
Тогда Вася достигает своей цели при
То есть если , то Вася не сможет выполнить задуманное.
А при Васе достаточно разрезать полоску на
кусков размера
и
кусок размера
, при этом расположить
кусков
размера
он должен на расстояний не более
клеток друг от друга и от концов. (Чего он сможет достичь, так как
)
Ошибка.
Попробуйте повторить позже
Можно ли в таблице расставить натуральные числа от
до
так, чтобы числа, отличающиеся друг от друга на единицу,
располагались в клетках с общей стороной, а все точные квадраты попали в один столбец?
Допустим, что такая расстановка возможна. Заметим, что столбец точных квадратов не может быть ни первым, ни последним, так как у
точных квадратов соседних чисел, а в одном соседнем столбце можно уместить только
чисел. Таким образом, после удаления
столбца точных квадратов, таблица распадается на две непустые части, в каждой из которых число клеток кратно
Группа чисел между
двумя последовательными квадратами попадает в одну из этих частей, при этом числа
и
попадают в разные части, поэтому
такие группы чисел попеременно попадают то в одну часть таблицы, то в другую. Между
и
имеется
чисел.
Следовательно, в одну из частей попадет
чисел. Так как
не кратно
то требуемая расстановка
невозможна.
Нет
Ошибка.
Попробуйте повторить позже
Квадрат (
) склеен в цилиндр. Часть клеток покрашена в черный цвет. Докажите, что найдутся две параллельных линии (две
горизонтали, две вертикали или две диагонали), содержащие одинаковое количество черных клеток.
Докажем утверждение от противного. Пусть есть раскраска, при которой отсутствует пара параллельных линий с одинаковым числом
черных клеток. Будем называть весом линии количество черных клеток на ней. Пусть есть горизонталь веса Тогда
вертикалей и
диагоналей каждого направления должны иметь веса
так как все они пересекают эту горизонталь. Тогда и
горизонталей
имеют веса
так как все они пересекают вертикаль веса
Циклически переставим горизонтали и вертикали так, чтобы нижняя
горизонталь и левая вертикаль имели вес
(свойства раскраски при этом не изменятся). Пронумеруем горизонтали снизу вверх от
до
а вертикали — от
до
слева направо. Каждая диагональ пересекает по разу горизонталь и вертикаль веса
поэтому
диагонали веса
должны проходить через клетку их пересечения — клетку
Итак, все клетки
и
не
закрашены.
Если нечетно, то в каждом столбце, кроме
получаем не менее двух незакрашенных клеток, и столбца веса
не найдется.
Если
, то столбец
и строка
должны иметь вес
(в любой из остальных строк и любом из остальных столбцов есть хотя
бы две незакрашенные клетки). Тогда в них закрашены все клетки, кроме
и мы не сможем найти столбца веса
Если с самого
начала отсутствует горизонталь веса
то есть горизонталь веса
и мы можем провести те же рассуждения, поменяв ролями
закрашенные и незакрашенные клетки.
Ошибка.
Попробуйте повторить позже
Фигура “мамонт” бьёт как слон (по диагоналям), но только в трёх направлениях из четырех (отсутствующее направление может быть
разным для разных мамонтов). Какое наибольшее число не бьющих друг друга мамонтов можно расставить на шахматной доске
Оценка. Из каждого мамонта выпустим три стрелки в тех направлениях, в которых он бьёт. Сопоставим стрелку диагонали (не обязательно
главной), если мамонт, из которого ведёт стрелка, стоит в этой диагонали, а стрелка идёт вдоль неё. Тогда каждой диагонали сопоставлено
не более двух стрелок: в противном случае две из них будут идти в одном направлении, и один из мамонтов будет бить другого. Поскольку
диагоналей всего (по
в каждом направлении), стрелок им сопоставлено не более
а значит, всего мамонтов не больше
Пример. Три возможных примера расположения мамонтов, не бьющих друг друга, показаны на рисунке.

Ошибка.
Попробуйте повторить позже
Фигура оборотень бьёт все клетки, находящиеся от неё через клетку слева, справа, сверху или снизу, а также бьёт клетку, на которой стоит.
Какое наименьшее количество оборотней необходимо поставить на клетчатую доску , чтобы эти фигуры били все клетки
доски?
Источники:
Подсказка 1
Оборотни на каких множествах клеток точно друг друга не бьют? Попробуем найти такие участки (множества клеток), на которых мы сможем оценить количество оборотней.
Подсказка 2
Оборотни, стоящие на квадрате 2*2, друг друга точно не бьют. Как, исходя из этого соображения, найти 4 множества клеток, которые замещают всю доску и в которых мы сможем оценить количество оборотней?
Подсказка 3
Рассмотрите множества клеток, получаемые всевозможными путями оборотня из каждой клетки углового квадрата 2*2. В каждом таком множестве по 16 клеток. Осталось лишь оценить количество оборотней в каждом таком множестве!
Раскрасим клетки доски в цвета следующим образом: все клетки, куда может прийти оборотень из, не умаляя общности, левой нижней
угловой клетки, покрасим в первый цвет. Сдвигами этого множества клеток вправо, вверх и вправо вверх получаем
множества
клеток.
![]()
Рассмотрим одно из них. Чтобы все клетки были побиты, нужно как минимум оборотня, так как каждый из них бьет не более
клеток, и, следовательно,
и меньше оборотней бьют максимум
клеток. Пример расстановки
оборотней: выделим
непересекающихся Т-образных фигур, в каждой из которых отметим по одному оборотню.
И так как оборотень, стоящий на клетке из одного множества, не может дойти до клеток из трех других, получаем, что всего нужно как
минимум оборотней.
Ошибка.
Попробуйте повторить позже
Можно ли в клетках квадрата расставить числа от 1 до 36 (каждое по одному разу) так, чтобы 6 сумм по горизонтали и 6 сумм по
вертикали в некотором порядке являлись 12 последовательными числами?
Источники:
Подсказка 1
Обозначим первую из 12 последовательных сумм за n. Какие числа входят в эти суммы? Что можно сказать о сумме всех сумм по горизонтали? А по вертикали?
Подсказка 2
Заметим, что при подсчёте всех горизонтальных сумм мы каждое число в таблице посчитали один раз. Тогда чему будет равна сумма всех таких 12ти сумм?
Подсказка 3
Удвоенной сумме всех чисел в таблице. Может ли быть такое? Проверим уравнением
Предположим, что можно. Сумма всех чисел равна . А удвоенная их сумма равна
. Посчитав
суммы арифметических прогрессий, получаем
Противоречие, так как
Ошибка.
Попробуйте повторить позже
В клетчатом квадрате две клетки одной строки или столбца назовем диполем, если между ними ровно две клетки. Петя решил
отметить как можно больше диполей, закрашивая разными цветами разные диполи (а обе клетки одного и того же диполя — одним цветом).
Какое наибольшее количество диполей он сможет закрасить?
Источники:
Подсказка 1
Это клетчатая задачка на оценку + пример, в которой даже персонаж намекает на способ решения, ведь он как-то там хитро закрашивает доску. А не поможет ли нам какая-то раскраска для получения оценки? Они часто помогают в таких задачах)
Подсказка 2
Давайте разобьём квадрат на 9 маленьких квадратиков 2 на 2 так, что между любыми двумя расстояние в 1 клеточку, и покрасим каждый из них в 4 цвета так, чтобы пары одинаковых цветов могли образовывать диполь. Как нам тогда поможет такая раскраска доказать оценку?
Подсказка 3
Так как у нас нечётное кол-во каждого цвета, то как минимум 4 клетки мы потеряем, а значит, уже не более 60/2 = 30 диполей можно получить, остаётся только нарисовать правильный пример под нашу оценку.
Рассмотрим в нашем квадрате квадратов
.png)
Назовём их выделенными.
Заметим, что если одна клетка некоторого диполя принадлежит какому-то выделенному квадрату, то другая клетка этого диполя принадлежит (соседнему) выделенному квадрату.
На рисунке отмечены номерами клетки в выделенных квадратах, так что у любого диполя обе клетки должны иметь один и тот
же номер. Но клеток с данным номером (например, с номером
) девять, и поэтому при “распределении” клеток с номером
по диполям
по меньшей мере одна клетка окажется нераспределённой (лишней). Таким образом, для каждого из четырех номеров остаётся
нераспределённой минимум одна клетка среди выделенных квадратов, а значит, всего имеется минимум
нераспределенные
клетки.
Получаем оценку: максимальное число непересекающихся диполей во всём квадрате не больше
Построим теперь пример на диполей. Для этого “отрежем” левый нижний выделенный квадрат. Останется клетчатая
фигура из
клеток, которая разбивается на квадрат
и два прямоугольника
и
. Эта фигура полностью
разбивается на диполи, поскольку любые последовательные
клеток строки или столбца, очевидно, разбиваются на три
диполя.
Ошибка.
Попробуйте повторить позже
Клетки квадрата покрашены в
цвета в шахматном порядке. Разрешается перекрасить все клетки в любом
прямоугольнике
Можно ли с помощью таких операций добиться того, чтобы все клетки квадрата стали одного
цвета?
Предположим, что мы сумели получить раскраску, в которой левый нижний угол поменял цвет (не умаляя общности, можно
рассмотреть этот случай, потому что какой-то угол цвет поменял). Введем координаты клеток так, чтобы у левого нижнего угла
были координаты а оси направим вправо и вверх. В клетки, у которых сумма координат делится на
поставим
флажки. Все клетки, кроме нижнего квадрата
легко разбить на
полосок
Каждая полоска
содержит ровно один флажок, ожидающий смены цвета, — всего
флажков плюс еще один флажок в левом нижнем углу.
Итого, мы должны сменить цвет у нечетного числа флажков. Но каждое перекрашивание меняет цвет ровно двух флажков.
Противоречие.
Нельзя
Ошибка.
Попробуйте повторить позже
Клетки доски покрашены в шахматном порядке. Стоящая на доске фигура кузнечик держит под боем все клетки своей
горизонтали, имеющие тот же цвет, что и клетка, на которой она стоит, а также все клетки своей вертикали, имеющие противоположный
цвет. (Чтобы побить какую-то клетку, кузнечик может перепрыгивать через другие фигуры.) Какое наибольшее число не бьющих друг друга
кузнечиков можно расставить на этой доске?
Оценка. В каждой горизонтали может стоять не более двух кузнечиков. Действительно, если в какую-либо горизонталь поставить трёх
кузнечиков, какие-то два обязательно окажутся на клетках одинакового цвета, и значит, будут бить друг друга. Поскольку доска содержит
горизонталей, число кузнечиков не может превышать
Пример. Существует много оптимальных расстановок, Например, достаточно занять кузнечиками вертикальных ряда, как
показано на рисунке. В каждой горизонтали стоит два кузнечика, поэтому суммарное число кузнечиков равно как раз
![]()
Ошибка.
Попробуйте повторить позже
Какое наименьшее количество клеток можно отметить на доске так, чтобы среди любых двух соседних клеток хотя бы одна из них
была отмечена, а также в любой строке и любом столбце были отмечены как минимум две соседние клетки?
Разобьем доску на прямоугольника
Докажем, что в каждом из них отмечено не менее
клеток. Разобьем прямоугольник на
квадратика
В каждом из них отмечена хотя бы
клетки, причем если их ровно
то они диагональные. Тогда в каждом
прямоугольнике клеток не меньше
причем, если их ровно
то каждая строчка раскрашена в шахматном порядке, но так не может
быть, поскольку в каждой строчке должны найтись
соседние отмеченные клетки. Поэтому всего отмечено не менее
клеток.
Осталось привести пример на отмеченных клеток:




