Пусть точка — центр , а — центр окружности основания конуса. . Продлим стороны до пересечения в точке . Введём прямоугольную декартовую систему координат, как на рисунке: — начало координат, ось направим вдоль , вдоль , вдоль .

Сделаем гомотетию с центром в точке так, чтобы центр окружности перешёл в точку . Сама же точка

Найдём уравнение плоскости , содержащую окружность конуса с центром в точке . Так как — служит осью конуса, то в качестве вектора нормали возьмём .

Так как , то

Найдём уравнение плоскости :

Возьмём в качестве , тогда получим

Найдём уравнение прямой :

Сложив первое уравнение, умноженное на , со вторым и, выразив , получим . Откуда можно подставить в первое уравнение и выразить . Тогда уравнение прямой в параметрическом виде:

Её направляющий вектор .

Пусть — точка касания окружности с плоскостью , тогда лежит на прямой , , :

Тогда

Уравнение плоскости :

Найдём уравнение прямой :

Подставляя во второе уравнение и выражая x, получим параметрическое уравнение прямой :

Её направляющий вектор .

Пусть — точка касания окружности с плоскостью , тогда лежит на прямой , ,

В силу симметрии картинки относительно плоскости , если окружность касается плоскости , то она будет касаться и плоскости , поэтому для касания всех трёх плоскостей, содержащих граней необходимо и достаточно выполнения уравнения:

Тогда

Рассмотрим

Пусть уравнение искомой плоскости имеет вид: , её нормаль , раз она проходит через точку , то удовлетворяет уравнению плоскости:

Обозначим нормали плоскостей и за и соответственно. Используем тот факт, что синус угла между плоскостями совпадает с синусом угла между их нормалями. Рассмотрим случай, когда углы между плоскостями совпадают с углами между их нормалями:

Мы получили систему с уравнениями и неизвестными:

Пусть , рассмотрим первые уравнения, после их сложения получим:

Подставим в первое уравнение:

Теперь подставим и в третье уравнение:

Возьмём , тогда , и наша искомая плоскость:

Найдём параметрическое уравнение прямой, относительно которой будем отражать точку . Так как наша прямая перпендикулярна плоскости , то в качестве направляющего вектора можно взять вектор нормали этой плоскости, а в качестве стартовой точки возьмём . Тогда уравнение нашей прямой выглядит так:

Возьмём точку на прямой так, чтобы , тогда

, симметричная относительно прямой , получается сдвигом на

Центр сферы, вписанной в куб, является центром куба, а радиус сферы равен половине его ребра, т. е. . Поэтому, если точка, в которой прямая касается сферы, то и .

В прямоугольной системе координат координаты точек: , , поэтому

Пусть тогда Из условий , и следует, что

Отсюда

Но , а для точки , лежащей на грани , поэтому , следовательно,

Таким образом,

откуда

Итак

Введём прямоугольную декартовую систему координат, как на рисунке: — начало координат, ось направим вдоль , в плоскости в сторону , вдоль .

а) Найдём координаты вектора :

Найдём координаты вектора :

Предварительно найдём координаты точки и :

Высота в треугольнике из вершины по т. Пифагора равна , а значит

Найдём их скалярное произведение: . что и требовалось доказать

б) Составим уравнение плоскостей:

Пусть , тогда, решая систему, получим: , за вектор нормали к этой плоскости возьмём .

Пусть , тогда его и возьмём за вектор к плоскости .

Угол между плоскостями:

Отношение объём пирамид с общим трёхгранным углом равно произведению отношений длин рёбер, исходящих из этого угла,

где Поскольку треугольники и равны, Значит,

Дальше можно было бы строить сечение и использовать для подсчёта отношений теоремы Фалеса и Менелая, но мы воспользуемся координатно-векторным методом.

— параллелограмм, поэтому и, следовательно,

Если точка принадлежит плоскости а коэффициенты и удовлетворяют уравнению (это, как известно, уравнение плоскости, даже если система координат не декартова, а точки и этому уравнению, очевидно, удовлетворяют).

Получаем

Обратная величина является ответом к задаче.

Опустим везде обозначения векторов, поскольку больше ничего использовать не будем.

Итак, рассмотрим треугольник, образованный векторами , и . Он равен треугольнику, образованному векторами , и по трём сторонам. Но тогда равны углы , что и требовалось доказать (поскольку треугольники образованы векторами, то это и будут углы между прямыми).

Пусть касание боковой стороны происходит в точке . Рассмотрим треугольники и . Нетрудно видеть, что они равны (общая гипотенуза, равные по радиусу стороны и перпендикулярность из касания), откуда , и тогда , то есть треугольники и равны (для треугольника : — и высота, и медиана), . Если опустить в пирамиде высоту , то , и — половина диагонали квадрата в основании. Из прямоугольного треугольника находим высоту Тогда найденное равенство в терминах координат (которые мы вводим с центром в точке , осью параллельно и сонаправленно вектору , а две другие оси по сторонам квадрата в основании), мы получаем, что

Возводим в квадрат обе части нашего уравнения и получаем

Соответственно объём равен

Введем декартову систему координат с началом координат в точке , ось направим вдоль , ось – на плоскости основания перпендикулярно оси абсцисс, а ось перпендикулярно плоскости основания тетраэдра.

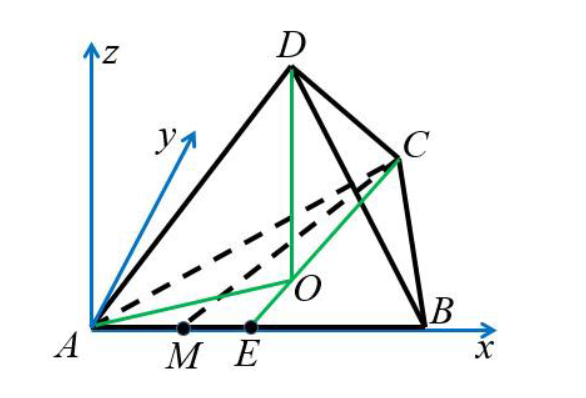
Из условия . Пусть – середина . Так как все ребра тетраэдра равны , то радиус окружности, описанной около равностороннего треугольника в основании: .

Радиус окружности, вписанной в основание: .

Из прямоугольного треугольника находим высоту пирамиды:

Высота равностороннего треугольника со стороной : .

Теперь можно выписать координаты всех нужных точек: , , , .

Таким образом

Напишем уравнение плоскости, проходящей через ребро параллельно . Найдем вектор, перпендикулярный этой плоскости

Уравнение искомой плоскости:

Искомая в задаче величина равна расстоянию от точки до этой плоскости:

Введем декартову систему координат с началом координат в точке , ось направим вдоль , ось – на плоскости основания перпендикулярно оси абсцисс и ось перпендикулярно плоскости основания.

Обозначим ребро куба через , отношения , .

Выписываем координаты нужных нам точек: , , , .

Находим уравнение плоскости в виде , подставив координаты точек . При этом так как плоскость не проходит через начало координат, то без ограничения общности можно считать, что .

Получим систему:

Откуда получаем, что

Находим расстояние от точки до плоскости по формуле

, где - координаты точки .

Получим

Опустим перпендикуляры из точки на плоскости и соответственно. Обозначим , , Согласно условию составим систему уравнений

Отсюда находим , , Обозначим длины рёбер , и через и соответственно.

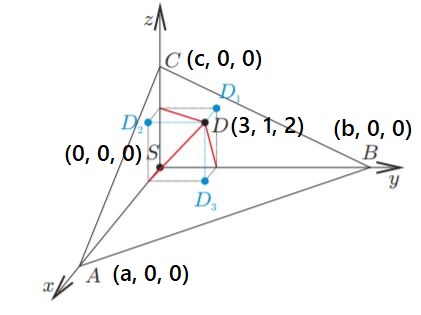
Лемма:

Доказательство: Введём систему координат с началом в точке как на рисунке. Запишем уравнение плоскости .

Так как плоскость не проходит через начало координат, то . Значит можно поделить на . Получим:

Теперь поставим в уравнение плоскости точки, в ней лежащие, чтобы найти коэффициенты , , . Итого получим, что , , . А значит уравнение плоскости

Подставив туда координаты принадлежащей этой плоскости точки , получим Лемма доказана.

Из неравенства между средним арифметическим и средним геометрическим для трёх переменных получаем:

причём равенство имеет место при Объём пирамиды поэтому Равенство имеет место при , ,

Рассмотрим систему координат с центром в основании высоты пирамиды, одну из осей направим вдоль самой высоты. Тогда длина проекции на эту ось, то есть соответствующая координата, каждого вектора будет равна нулю для рёбер из основания и иметь одинаковое по модулю значение для боковых рёбер — длина высоты с положительным или отрицательным знаком.

Чтобы сумма векторов была нулевой необходимо, чтобы сумма этих координат (соответствующая координата суммы) была равна нулю.

Пусть длина высоты равна и координат из ненулевых положительны, тогда эта координата равна

Но поскольку по чётности, а также из условия, значит, нулевой сумма векторов-рёбер быть не может.