Ошибка.
Попробуйте повторить позже
Коническое (пожарное) ведро было заполнено водой до самого края.

В него положили шар, причем он полностью покрылся водой. Покажите, что при этом из ведра вылилось не более половины бывшей там воды.
Источники:
Подсказка 1
Если мы хотим доказать, что что-то меньше чего-то, то нам надо взять это что-то максимальным, а после этого доказать, что даже в этом случае выполняется требуемое. Шар у нас лежит не выше уровня воды, при этом, он касается поверхности конуса. В какой ситуации тогда радиус шара будет максимальным(ну а значит и его объем)?
Подсказка 2
Предельное положение - это когда шар вписан в конус. А значит, окружность радиуса такого же как у шара вписана в сечение конуса, которое проходит через диаметр окружности в основании и вершину. Значит, мы можем взять за r - радиус шара, за h - высоту конуса и за R - радиус окружности в основании конуса и тогда картинка однозначно фиксируется и все через все выражается. Сделайте это и поймите связь между r и парой h и R. Чему тогда равно отношение объемов(ведь этого от нас и просят)?
Подсказка 3
Отношение объемов равно, в силу того, что (h - r)/r = sqrt(h^2 + R^2)/r, 4 * (h / r) * (1 - 2 * (h/r)). Мы хотим максимизировать объем, значит, надо взять максимум у этой параболы(у нас же относительно h/r - выражение представляется графически параболой), а она не больше 1/2.
Обозначим радиус шара через радиус основания конуса через
а высоту конуса — через
Тогда объём конуса
равен
Объём шара
Отношение этих объемов равно
Можно считать, что верхняя точка шара находится на поверхности воды, иначе воды выльется ещё меньше.
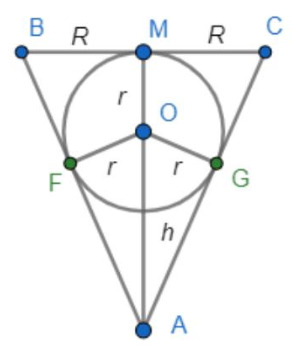
Из подобия прямоугольных треугольников и
имеем
Возведем равенство в квадрат, получим
Значит, отношение объёмов равно
где Максимум этой функции достигается в вершине параболы, то есть при
и составляет
Заметим, что максимум достигается при при этом
Ошибка.
Попробуйте повторить позже
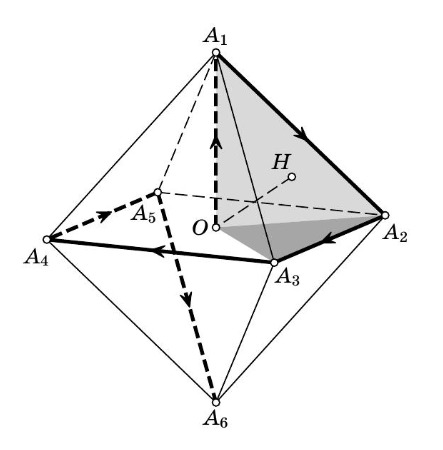
Сфера касается основания
тетраэдра
в точке
и проходит через вершину
. Рёбра
и
эта сфера
пересекает в точках
и
. Центр описанной окружности треугольника
лежит на отрезке
. Радиус сферы
равен
.
Пусть - объём тетраэдра
, а
- объём тетраэдра
. Какое наибольшее значение может принимать
Источники:
Пусть — центр описанной окружности треугольника
, лежащий на
— центр сферы. Очевидно,
— середина
.
Так как точки
и
лежат на сфере,
перпендикулярно плоскости
. С другой стороны,
и
— это одна и
та же прямая, а
перпендикулярна плоскости
. Значит, плоскости
и
параллельны, а тетраэдры
и
подобны.
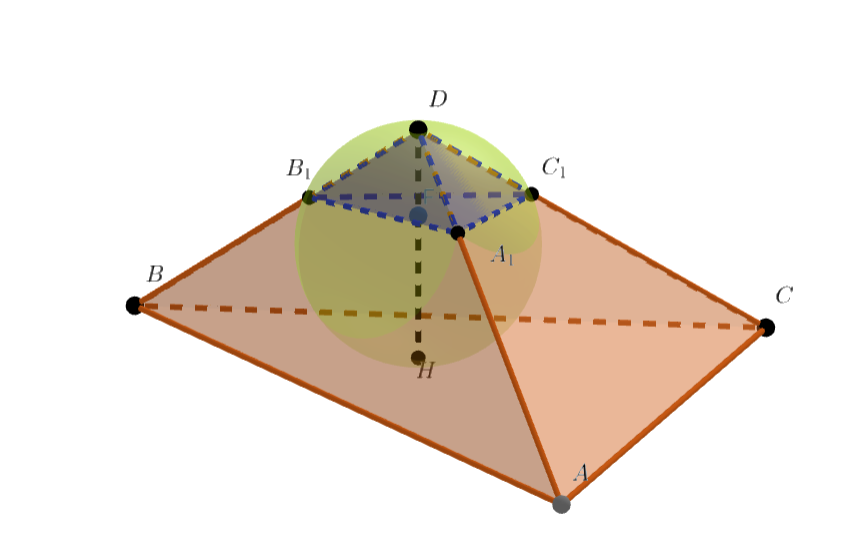
Пусть — длина
, то есть высота маленького тетраэдра. Высота большого тетраэдра равна
, а коэффициент их подобия
.
- прямоугольный треугольник с прямым углом
, значит, радиус описанной окружности
треугольника
, то есть
, равен
Как известно, среди всех треугольников, вписанных в данную окружность, наибольшую площадь имеет равносторонний. Для окружности
радиуса эта площадь составляет
Значит, объемы тетраэдров составляют
и
а их произведение равно
Чтобы максимизировать эту величину, достаточно максимизировать
В первой точке достигается минимум, равный нулю, а во второй — максимум. Подставив в формулу для объёма,
получим
Ошибка.
Попробуйте повторить позже
Дана правильная шестиугольная пирамида (
— вершина) со стороной основания
и боковым ребром
Точка
лежит
на прямой
точка
— на прямой
причём отрезок
параллелен плоскости
(или лежит в ней). Найдите наименьшую
возможную длину отрезка
Источники:
За будем обозначать плоскость, проходящую через точки
,
и
Возьмем на прямой такую точку
, что
. Тогда
На прямой же возьмем точку
такую, что
. Получается, что плоскость
Тогда
лежит в плоскости
.
пересекает плоскость основания по прямой
(
), параллельной
![]()
Пусть . Тогда
,
. Треугольник
будет правильным (есть 2 угла по
), т.е.
.
т.к. это 2 угла с параллельными сторонами.
Рассматриваем треугольник .
. Подставляем найденные значения.
Минимум выражения слева достигается при и равно
. Тогда
Ошибка.
Попробуйте повторить позже
На сфере расположены точки таким образом, что минимальные расстояния по поверхности сферы от точки
до точки
от
точки
до точки
и от точки
до точки
равны
и
соответственно. Найдите минимальный возможный при таких
условиях периметр треугольника
Источники:
Подсказка 1
Давайте сначала представим, что такое расстояние на сфере? Это дуга наименьшей длины окружности с центром, совпадающим с центром сферы. Тогда какую оценку на радиус сразу можно понять из условия?
Подсказка 2
Верно, радиус не может быть меньше 5, как тогда получается наибольшая длина окружности 10π, а половина меньше 5π. Давайте теперь поймём, как можно посчитать стороны треугольника ABC. Любые две точки на сфере лежат также на окружности с радиусом сферы. Какую тогда теорему можно вспомнить, связанную с этими величинами?
Подсказка 3
Точно, это теорема синусов. Но проблема с углом напротив стороны, кажется, что мы его не знаем. А что такое угол напротив стороны с точки зрения длины дуги в радианах и радиуса?
Подсказка 4
Верно, это по формуле отношение длины дуги к радиусу. Причём помните, что у нас есть ограничение на длину дуги. Мы берём наименьшую, а значит, не больше, чем половину длины окружности. Сложив теперь аналогичные длины сторон, получим периметр нашего треугольника. Мы должны найти его минимальное значение. Посмотрим, от какой переменной зависит это выражение и не можем ли мы тогда проанализировать его как функцию?
Подсказка 5
Точно, оно зависит только от радиуса, а значит, можно исследовать выражение как функцию, взять производную и что-то понять про него. Например, что она возрастающая на некотором подходящем нам интервале. После этого мы переформулируем задачу на нахождение минимального радиуса. Как тогда можно понять, что функция возрастает? Попробуйте вынести косинус и вспомнить, что отношение дуги к радиусу у нас может быть равно только от 0 до π/2.
Подсказка 6
Ага, функция возрастает, потому что tgx>x, x ∈ (0; π/2). А у нас как раз такого вида выражение. Ура, уже хорошо! Теперь осталось оценить радиус. Какие есть мысли по этому поводу? Так как у нас должен быть минимальный радиус, то можно по минимуму "сжать" сферу. Тогда какой вариант радиуса подойдёт?
Подсказка 7
Верно, можно взять сферу радиуса 6, так как сложив наименьшую длину всех дуг по условию, то получим, что это длина окружности с радиусом 6. Осталось понять, почему нельзя взять меньший радиус. Попробуем взять на сфере радиуса 6 произвольную точку А. Тогда где могут находиться точки С, если смотреть на сферу с точки зрения глобуса? А исходя из этого, где лежат точки B?
Подсказка 8
Верно, так как расстояние 3π, то эти точки будут расположены где-то на "экваторе". Теперь если рассмотрим возможные расстояния от С до B, то они снова будут лежать где-то на параллели. Осталось только рассмотреть, какое максимальное расстояние в принципе возможно от А до В, и понять, почему любые смещения по "параллелям" и "меридианам" будут плохи. Победа!
Сначала необходимо заметить, что кратчайшее расстояние между двумя расположенными на сфере точками по ее поверхности это длина
меньшей дуги, проходящей через эти две точки окружности, центр которой совпадает с центром сферы. Отсюда сразу следует
первая оценка на радиус сферы: он не может быть меньше, чем В противном случае длина самой большой окружности,
расположенной на сфере, меньше, чем
, и длина ее меньшей дуги будет меньше, чем
что противоречит условию
задачи.
![]()
Обозначим радиус сферы за ее центр обозначим буквой
Рассмотрим две произвольные точки
пусть длина дуги
равна
отметим, что
Из сектора и треугольника
имеем:
Из этой формулы следует, что периметр треугольника равен:
Рассмотрим функцию одной переменной:
Тогда что положительно при
так как
Обратим внимание, что все три слагаемых, входящих в периметр, являются такого сорта функциями, при этом радиус не может быть
меньше, чем 5 и, следовательно, величина
во всех трех слагаемых принадлежит полуинтервалу
Поэтому периметр
треугольника
является возрастающей функцией параметра
и, следовательно, задача сводится к следующей: найти
минимальный радиус сферы, на которой могут быть расположены точки
удовлетворяющие данным из условия
задачи.
Обоснование того, что минимальный радиус равен состоит из двух тезисов. Во-первых, на сфере радиуса
расположить три точки в
соответствии с условием задачи можно: достаточно взять экватор сферы, его длина равна
что равно сумме данных в условии
расстояний. Берем произвольную точку
на этой окружности, проходим по часовой стрелке расстояние
отмечаем точку B, проходим
еще
отмечаем точку
Во-вторых, на сфере радиуса, меньшего чем 6, точки расположить не получится. Чтобы это доказать, проведем аналогию с глобусом.
Представим себе, что точка это северный полюс планеты радиуса 6. Тогда геометрическим местом точек
кратчайшее расстояние от
которых по сфере до точки
равно
будет параллель-«экватор», а геометрическим местом точек
кратчайшее расстояние от
которых по сфере до точки
равно
будет параллель в южном полушарии. Максимальное расстояние между точкой с «экватора» и
точкой с «южной» параллели как раз равно
и будет достигаться в случае, когда эти точки расположены на противоположных
меридианах. Любые меридиональные смещения одной из точек, очевидно, уменьшат расстояние между ними. Попытка уменьшить радиус
сферы-планеты приведет к тому, что параллели, на которых лежат точки
и
сместятся ближе к южному полюсу, и максимальное из
расстояний между точками с этих параллелей (которое по-прежнему достигается в случае их расположения на противоположных
меридианах) уже будет менее, чем
Итак, минимально возможный радиус сферы равен 6, откуда получаем ответ:
Ошибка.
Попробуйте повторить позже
Середины всех высот некоторого тетраэдра лежат на его вписанной сфере. Верно ли, что тетраэдр правильный?
Источники:
Подсказка 1
Попробуем разобраться в этом тетраэдре. Мы знаем, что середина каждой высоты лежит на вписанной сфере. Какое неравенство, связанное с высотой и радиусом вписанной сферы, мы можем получить?
Подсказка 2
Если Hi- длина произвольной высоты тетраэдра, то Hi/2<=2r, где r- радиус вписанной сферы. Это можно увидеть, если провести плоскость, параллельную плоскости основания высоты и касающуюся вписанной сферы. Что же может дать нам это неравенство? Полезно было бы вспомнить о том, что Hi и r связаны объёмом тетраэдра...
Подсказка 3
Обозначим за Si- площадь произвольной боковой грани. Тогда: 3*V=Hi*Si=r*(S1+S2+S3+S4), где V- объем тетраэдра. Попробуйте теперь воспользоваться неравенством Hi/2<=2r...
Подсказка 4
Подставив неравенство в равенство, мы получим, что: r*(S1+S2+S3+S4)<=4*r*Si. Сократим обе части на 4*r: (S1+S2+S3+S4)/4<=Si. Получается, что произвольно выбранная площадь не меньше среднего арифметического всех площадей. Это как-то странно...
Подсказка 5
Давайте предположим, что Si не больше всех оставшихся площадей. Тогда: Si=(Si+Si+Si+Si)/4<=(S1+S2+S3+S4)/4<=Si. Это означает, что все Si равны между собой. Тогда и все высоты равны между собой. Во что превращается неравенство Hi/2<=2r?
Подсказка 6
Положим, что S1=S2=S3=S4=S, а H1=H2=H3=H4=H. Т.к. H*S=r*(S1+S2+S3+S4) получаем, что H=4r. Но тогда высоты обязаны содержать центр вписанной окружности и точку касания с гранью. Может как-то выразить длины ребер через высоты...
Подсказка 7
Для определенности проведем высоту AH и будем искать ребро AB. По теореме о касательной и секущей получаю, что BH^2=H*H/2. Теперь осталось воспользоваться теоремой Пифагора для треугольника ABH и увидеть, как AB выражается через H.
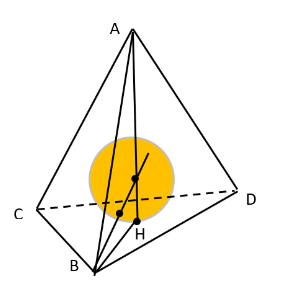
Рассмотрим тетраэдр удовлетворяющий условию задачи. Заметим, что по условию для любой высоты
данного тетраэдра
справедливо неравенство
где
— радиус вписанной сферы, то есть
Пусть — площадь грани, на которую опущена высота
Докажем, что
Предположим противное. Выберем
грань минимальной площади (если таких граней несколько, то берём любую из них). Без нарушения общности можно считать, что её
площадь равна
(иначе можно ввести переобозначения). Так как не все
равны между собой и
- наименьшая из них,
то
Выразим объём тетраэдра двумя способами:
Отсюда что противоречит неравенству
Итак, все равны, поэтому все
равны, так как
Обозначим за
длину этих равных высот. Из приведённого выше
соотношения для объёма получаем
то есть неравенство обращается в равенство. Но это возможно только в случае, если высота
содержит центр сферы и точку касания с гранью (и так для каждой высоты).
Пусть - основание высоты тетраэдра, опущенной из точки
Тогда
совпадает с точкой касания сферы и грани
Пусть
тогда по теореме о касательной и секущей
По теореме Пифагора из прямоугольного треугольника
получаем
Аналогично получаем такое же выражение для остальных рёбер тетраэдра, следовательно, они равны между собой, то есть тетраэдр правильный.
Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида , основание которой — равносторонний треугольник
, а все плоские углы при вершине
равны
. При каком наименьшем
можно утверждать, что эта пирамида правильная?
Источники:
Подсказка 1
Эта задача на оценку + пример. Давайте попробуем сначала привести пример для угла, который, как нам кажется, подходит. А потом уже докажем, что для меньшего угла условие задачи не выполняется. Подумайте какой хороший угол нам подойдёт? Слова про правильные фигуры на это всячески намекают.
Подсказка 2
Верно, докажем, что при плоском угле 60 градусов наша пирамида окажется правильной. Нужно только понять, что если в треугольнике есть угол 60 градусов, то сторона напротив него средняя по величине между другими. Тогда предположив, что какое-то боковое ребро не равно ребру из основания, сможем получить противоречие и получить доказательство. Что же будет, если плоские углы будут меньше 60? Попробуйте построить пример неправильной пирамиды с таким углом, учитывая условия задачи и соотношения сторон по их размерам.
Подсказка 3
Давайте, рассмотрим равнобедренный треугольник SAB, в котором SA=SB и ∠S = α(α<60). Тогда сторона AB в нём наименьшая, и мы сможем его отложить на боковых сторонах. Осталось только понять, что отложив на рёбрах трёхгранного угла нужные отрезки(два из которых SA и SB) с плоскими углами меньше 60, мы получим неправильную пирамиду, то есть контрпример.
Докажем, что при пирамида правильная. Пусть стороны треугольника
равны 1. Заметим, что в любом треугольнике с
углом
против этого угла лежит средняя по длине сторона (причём если она строго меньше одной из сторон, то строго больше другой).
Пусть одно из боковых рёбер пирамиды не равно 1: например,
. Тогда в гранях
и
рёбра
и
будут меньше 1, и
значит, в грани
ребро
— не средняя сторона, противоречие.
Покажем теперь, как построить неправильную пирамиду с плоскими углами при вершине
.
Первый способ. Сначала боковое ребро удаляем, а неудалённую боковую грань
вращаем вокруг её ребра
основания
, пока эта грань не окажется в плоскости основания так, что будет содержать треугольник основания. В
процессе движения будут «текущие» пирамиды, у которых два равных плоских угла сначала равны
, потом больше
(в
момент, когда вершина проектируется в вершину основания — поскольку в этот момент синус угла при вершине
в
боковых гранях
и
равен
, а в грани
равен отношению боковой высоты этого треугольника к
,
которая меньше 1), а в конце у «вырожденной» пирамиды они равны
. Значит, в силу непрерывности, будет ещё раз
.
Второй способ. Рассмотрим треугольник c
и
. Так как
, на стороне
существует такая точка
, что
. Теперь возьмем трёхгранный угол, у которого все плоские углы равны
, и отложим на его ребрах отрезки
,
,
. Пирамида
— искомая.
Третий способ. Пусть — правильная пирамида с плоским углом
при вершине
. Пусть
,
— точки, такие, что
, построим на
треугольники
и
так, что
,
,
,
тогда понятно что
. В силу теоремы синусов для этих треугольников имеем
что влечёт , поскольку синусы смежных углов равны. Пусть теперь
— такая точка на продолжении отрезка
за
точку
, что
. Тогда
,
, и
, тогда
,
откуда
, и значит
(по трём сторонам). Из всех указанных равенств треугольников следует,
что у пирамиды
все плоские углы при вершине
равны
, значит она удовлетворяет условиям задачи. Но она не правильная,
поскольку прямая
не перпенидикулярна
, и на ней только одна точка проецируется в центр треугольника
, это точка
,
а значит не точка
.
Ошибка.
Попробуйте повторить позже
На поверхности правильного тетраэдра построена замкнутая линия, каждая точка
которой обладает следующим свойством:
длина кратчайшего пути по поверхности тетраэдра между
и серединой ребра
равна длине кратчайшего пути по
поверхности тетраэдра между
и серединой ребра
. Найдите длину этой линии, если длина ребра тетраэдра равна
1.
Источники:
Подсказка 1
У нас тут рассматривается расстояние по поверхности...Как можно перевести картинку на плоскость в таком случае, чтобы было более удобно?
Подсказка 2
Рассмотреть развертку! Вот пусть мы развернули его так, что получился ромб ABCD, где AC - общее ребро у развернутых граней. Но все еще непонятно как работать с линиями ломаной, которые не получится нормально нарисовать на развертке. Что можно в таком случае придумать?
Подсказка 3
Давайте мысленно "порежем" нашу ломаную ребрами и отрезками AN, BN, CM, DM, где M и N - середины AB и CD, и рассмотрим только ту часть ломаной, что внутри треугольника AMC на нашей развертке. Наверное, в этом треугольнике не сложно найти такие точки на развертке?
Подсказка 4
Например, пусть P - точка ломаной внутри AMC. Понятно, что кратчайший путь от P до M - это PM, а кратчайший путь от P до N - это отрезок PN). Такие отрезки должны быть равны, а значит какое ГМТ у P?
Подсказка 5
Серединный перпендикуляр к MN! Достаточно легко теперь найти длину этой ломаной внутри AMC. А что делать с остальными частями этой ломаной? Вот что: попробуйте осознать, что они будут такими же, например, из соображений симметрии)
Пусть и
— середины ребер
и
соответственно. Из соображений симметрии ясно, что ребрами
и отрезками
линия, о которой идет речь в условии задачи разбивается на 8 равных. Поэтому достаточно рассмотреть точки,
принадлежащие треугольнику
.
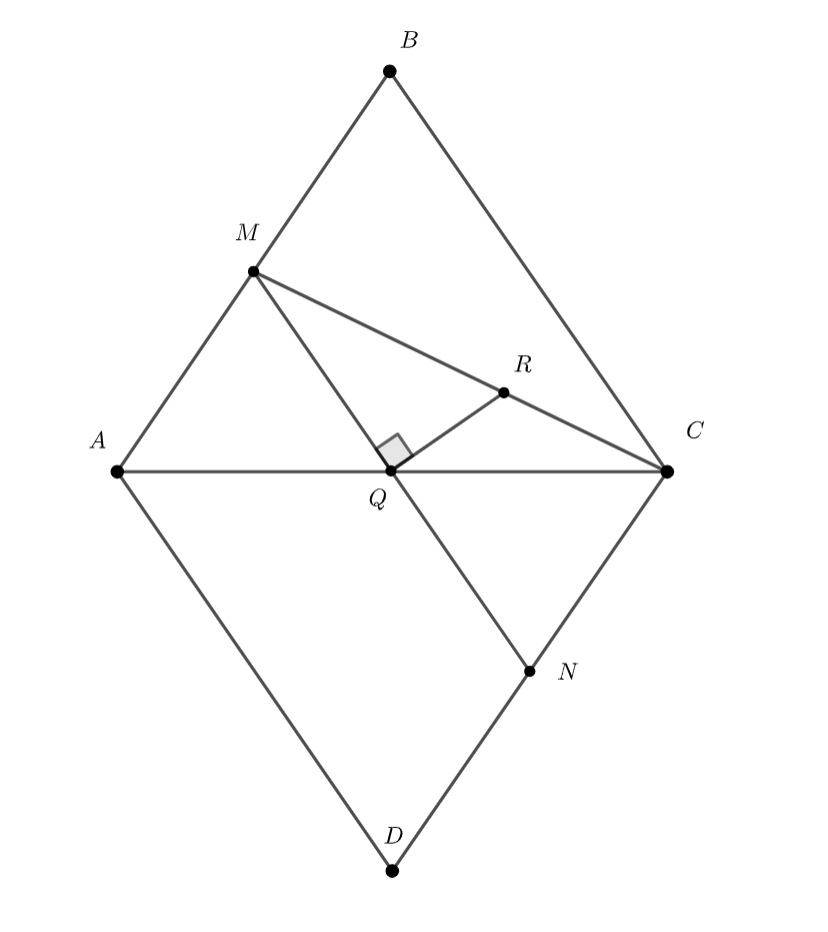
Пусть - одна из таких точек. Тогда кратчайшим путем между
и
служит отрезок
, а кратчайшим путем между
и
- двухзвенная ломаная
, вершина
которой принадлежит ребру
(в случае
имеем просто отрезок
. На развертке
тетраэдра объединение граней
и
представляет собой ромб
, а ломаная
- отрезок
в нем. Условие
означает, что
лежит на серединном перпендикуляре к отрезку
; следовательно геометрическим местом точек
служит отрезок
, где
- середина ребра
(и середина отрезка
)
- точка на отрезке
,
(см
рисунок).
Найдем длину отрезка . Легко видеть, что
, а отрезок
, будучи средней линией треугольника
, имеет длину
. Поэтому
Умножив это число на 8, получим ответ к задаче:
Ошибка.
Попробуйте повторить позже
В 2022 году исполняется 65 лет запуска первого искусственного спутника Земли (ИСЗ). В настоящее время для обеспечения бесперебойной работы сотовой связи, систем теле и радиовещания используются различные виды спутников, находящихся на различных орбитах, на различных высотах.
Зоной покрытия спутника назовем часть поверхности земного шара, в пределах которой обеспечивается уровень сигналов к спутнику и от него, необходимый для их приема с заданным качеством в конкретный момент времени. Как правило, эта часть поверхности ограничивается окружностью, проходящей по линии видимого горизонта. На рисунке линия проходит через точку Г:
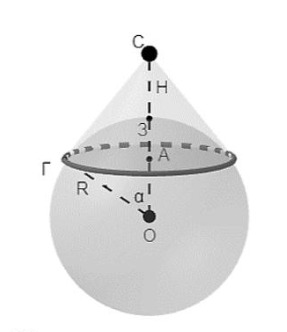
a) Определите площадь земной поверхности ( ), которая является зоной покрытия спутника, находящегося на высоте
км
относительно земной поверхности, считая ее сферой радиуса
км с центром в точке
б) Найдите все значения для которых на поверхности земли можно расположить окружности
каждая из которых
внешним образом касается окружности
с центром в точке
и радиусом
каждая из них является границей зоны покрытия
ИСЗ, находящегося на той же высоте
, что и спутник с зоной покрытия
Каждая из зон покрытия
должна внешним образом
касаться окружностей
и
т.е. первая касается
и
вторая —
и
и т.д. Окружность
должна
касаться
и
Источники:
а) Зона покрытия — часть сферы, лежащая внутри конуса. , где
— высота сегмента.
, здесь угол
—
угол между радиусом ОГ и линией ОА, соединяющий центр сферы с центром окружности, которая является линией пересечения сферы и
конуса.
Тогда площадь равна
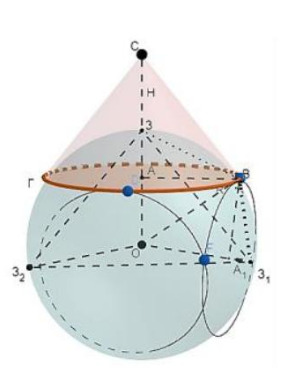
б) Пусть О — центр сферы, В — точка касания первой и второй окружности, А и их центры этих окружностей,
— точки
пересечения радиусов
со сферой. Обозначим
— угол между ОЗ и ОВ. Тогда
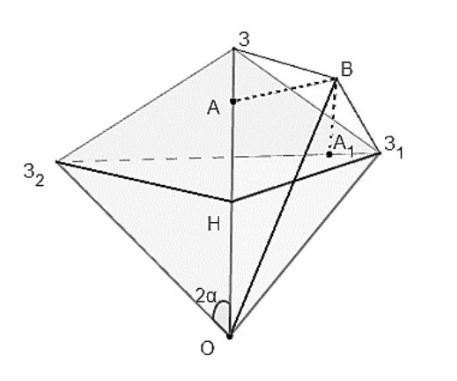
В правильной пирамиде О плоские углы при вершине равны
двугранный угол при ребре О3 равен
Опустив
перпендикуляры из точек
и
на ребро О3 в точку H, треугольники О
и О
равны (по трем сторонам), т.к. две стороны
равны
а третья
а)
б)
Ошибка.
Попробуйте повторить позже
Звездолёт находится в полупространстве на расстоянии от его границы. Экипаж знает об этом, но не представляет, в каком направлении
двигаться, чтобы достигнуть граничной плоскости. Звездолёт может лететь в пространстве по любой траектории, измеряя длину
пройденного пути, и имеет датчик, подающий сигнал, когда граница достигнута. Может ли звездолёт гарантированно достигнуть границы,
преодолев путь длиной не более
Источники:
Подсказка 1
В условии сказано, что пройдя расстояние, равное a, в определенную сторону, звездолет покинет полупространство. Каким образом мы можем описать все варианты той точки, где кончается полупространство?
Подсказка 2
Мы можем сказать, что если звездолет находится в какой-нибудь точке О, то на сфере с центром в точке O и радиусом a гарантированно найдется точка , которая уже не будет являться частью полупространства. Подумайте, как данная сфера может помочь в выборе траектории. Может быть, есть какая-то фигура, которую удобно будет описать около сферы?
Подсказка 3
Рассмотрите правильный октаэдр, описанный около данной сферы. Если мы докажем, что путь из центра октаэдра по всем вершинам без повторений меньше 14a и хотя бы одна вершина гарантировано не лежит в полупространстве, то мы решим задачу. Сначала подумайте, как можно сделать второе.
Подсказка 4
Воспользуемся методом от противного. Подумайте, где возникает противоречие, если мы скажем, что все вершины октаэдра лежат в данном полупространстве.
Подсказка 5
Теперь нужно найти длину пути от О и по всем вершинам. Давайте назовем наш октаэдр A₁A₂A₃A₄A₅A₆, тогда не трудно найти кратчайший маршрут обхода: O -> A₁ -> A₂ -> A₃ -> A₄ -> A₅ -> A₆. Как можно найти длину данного пути?
Подсказка 6
Для начала нужно найти длину отрезка OA₁, так как из него легко можно выразить длину ребра октаэдра. Мы знаем, что длина высоты, опущенной из точки О на грань октаэдра равна a, Тогда как мы можем найти длину OA₁?
Подсказка 7
Давайте рассмотрим пирамиду OA₁A₂A₃, найдем ее объем двумя разными способами, как 1/6 куба с ребром OA₁ и через длину высоты и площадь A₁A₂A₃. Из равенства двух данных выражений легко можно выразить OA₁. Для окончательного решения останется только найти длину ребра и доказать, что предложенный нами маршрут меньше 14a.
Пусть корабль находится в некоторой точке Рассмотрим правильный октаэдр
описанный возле шара радиуса
с
центром в точке
Докажем, что путь
заведомо позволит достигнуть граничной
плоскости.
Предположим противное. Тогда вершины октаэдра, а значит, и сам октаэдр (выпуклая оболочка его вершин) лежат
строго внутри полупространства. Поэтому вписанный шар октаэдра, радиус которого равен тоже лежит строго внутри
полупространства. Получаем противоречие, так как по условию расстояние до граничной плоскости полупространства равно
Покажем теперь, что длина пути меньше
Пусть
— высота
пирамиды
Запишем ее объём двумя способами:
Отсюда получаем, что а длина ребра октаэдра равна
Поэтому длина пути равна
так как
Ошибка.
Попробуйте повторить позже
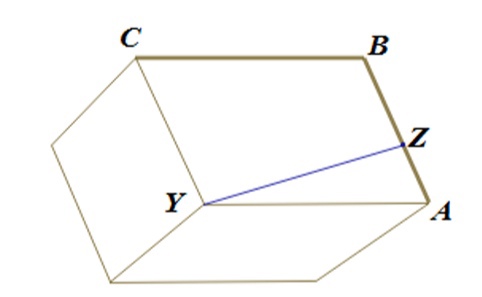
Дана пирамида вершина
которой лежит на одной сфере с серединами всех её рёбер, кроме ребра
Известно, что
Найдите длину ребра
Какой наименьший радиус может иметь сфера, описанная около данной
пирамиды?
Источники:
Подсказка 1
Во-первых, на что нам могут намекать середины сторон? На средние линии. А средние линии параллельны основаниям. Что мы можем из этого извлечь? Какие параллелограммы есть на картинке?
Подсказка 2
Во-первых, в силу свойства средней линии, ADCE и ABDP - параллелограммы. При этом они вписаны в сечения нашей сферой плоскостей ACD и PRS. А значит, эти параллелограммы - прямоугольники. А это дает много прямых углов, а значит - много перпендикулярностей. Какая прямая тогда перпендикулярна прямой RS? А что нам это дает?
Подсказка 3
Прямая PQ перпендикулярна прямой RS, из за того, что параллельные им прямые EA и AD перпендикулярны. Давайте опустим перпендикуляр QH на RS.
Подсказки 4
Тогда у нас плоскость QHP перпендикулярна RS. Значит, и прямая PH перпендикулярна RS. А значит, наш «согнутый» четырехугольник QRPS (то есть, мы можем повернуть треугольник QRS вокруг RS до момента, когда повернутый треугольник будет лежать в плоскости RPS) имеет взаимноперпендикулярные диагонали. А значит, две суммы квадратов противоположных сторон равны. А тогда мы нашли RP. А значит, у нас фиксированы две стороны прямоугольного треугольника RPS, и мы найдем его гипотенузу.
Подсказка 5
Остается дать оценку на радиус сферы, описанной вокруг тетраэдра. Ну какую самую глупую оценку можно дать? Что первое приходит в голову(с учетом того, что нам еще пример надо построить)?
Подсказка 6
Самая глупая оценка снизу - это то, что радиус не меньше радиуса описанной окружности треугольника QRS. Найти радиус нетрудно(мы знаем все три стороны). Остается привести пример.
Подсказка 7
Чтобы достигалось равенство, надо, чтобы у нас в плоскости QRS лежал содержался центр сферы. Впишем туда треугольник QRS.
Подсказка 8
Остается доказать, что на сфере найдется точка P’, такая, что треугольники PRS и P’RS равны(это по сути и значит, что получен тетраэдр, который подходит под условия). То есть по сути надо поворачивать треугольник P’RS, равный треугольнику PRS, вокруг RS, до того момента, как точка P’ не станет принадлежать окружности.
Пусть - середины рёбер
соответственно. Из теоремы о средней линии треугольника следует, что
и
- параллелограммы. Они вписаны в окружности, являющиеся сечениями сферы плоскостями
и
,
поэтому эти параллелограммы - прямоугольники. Угол
— прямой; прямые
и
перпендикулярны, так как
Отметим в плоскости точку
такую, что
а точки
и
лежат по разные стороны от прямой
(треугольник
может быть получен из треугольника
поворотом вокруг прямой
![]()
Из равенства треугольников и
следует, что основания их высот, опущенных на
— это одна и та же точка (назовём её
Плоскость
перпендикулярна
(так как
поэтому
Поскольку
и
то плоскость
перпендикулярна
и
Значит, диагонали четырёхугольника пересекаются под прямым углом (в точке
). По теореме Пифагора
Следовательно,
Из прямоугольного треугольника находим
Радиус сферы, описанной около пирамиды , не меньше радиуса
окружности, описанной около грани
. Пирамида, для
которой достигается равенство, существует. Докажем это.
![]()
Рассмотрим сферу радиуса и окружность - её сечение, проходящее через центр сферы. В сечении сферы указанной плоскостью
получится окружность с диаметром
, в которую можно вписать прямоугольный треугольник
. По теореме косинусов из
треугольника
находим, что
По теореме синусов
Ошибка.
Попробуйте повторить позже
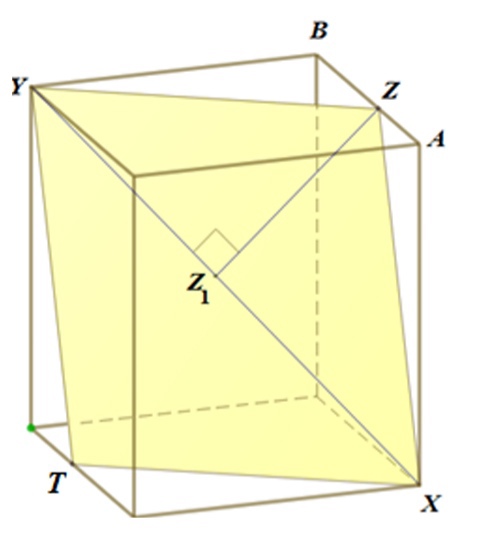
По диагоналям оснований и
куба
с ребром
ползут два муравья Гоша и Леша. Движение они начали
одновременно из точек
и
соответственно с постоянной скоростью, причем скорость Леши была в два раза больше скорости
передвижения Гоши и закончили, когда Леша оказался в точке
. Какое наименьшее расстояние разделяло Гошу и Лешу во время
движения?
Источники:
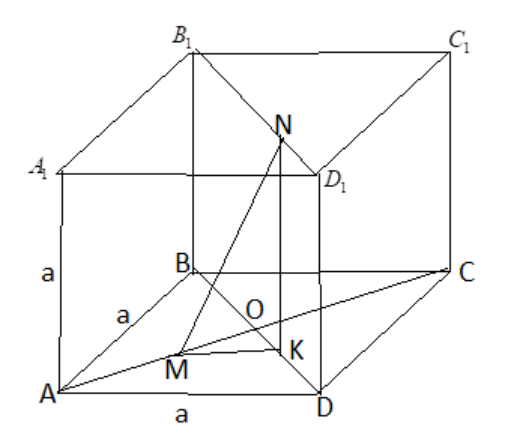
Фиксируем момент времени
— положение муравьёв в момент
.
— проекция точки
на диагональ
.
— скорость движения Гоши,
— скорость Леши.
Тогда имеем
Наконец,
Движение закончилось, когда последняя скобка занулилась, то есть при . Относительно
функция
является квадратным
трёхчленом с положительным коэффициентом при
. Вершина находится в точке
. Отсюда
.
Ошибка.
Попробуйте повторить позже
Дан куб с ребром
. Точка
— центр грани
. Найдите наименьшее значение суммы длин
, если точка
лежит на отрезке
.
Подсказка 1
Нам нужно найти наименьшее значение суммы длин двух отрезков. Но... Они лежат вообще в разных плоскостях- это неудобно. Совсем непонятно, что делать с ними в таком виде. Когда есть неудобство, пробуем от него избавиться! Как это можно сделать?
Подсказка 2
Верно, мы же можем расположить их в одной плоскости. Уже ситуация полегче. Вспомним о том, что нам надо найти - наименьшую сумму длин. Обычно это делается с помощью неравенства. А какое самое простое неравенство есть для двух отрезков?
Подсказка 3
Да, это неравенство треугольника! Ведь по нему сумма двух сторон должна быть больше третьей. Хм... Но тогда же получается, что если Е попадёт на третью сторону, то это и будет минимум. Осталось только подумать, зачем нам дали такую хорошую точку О.
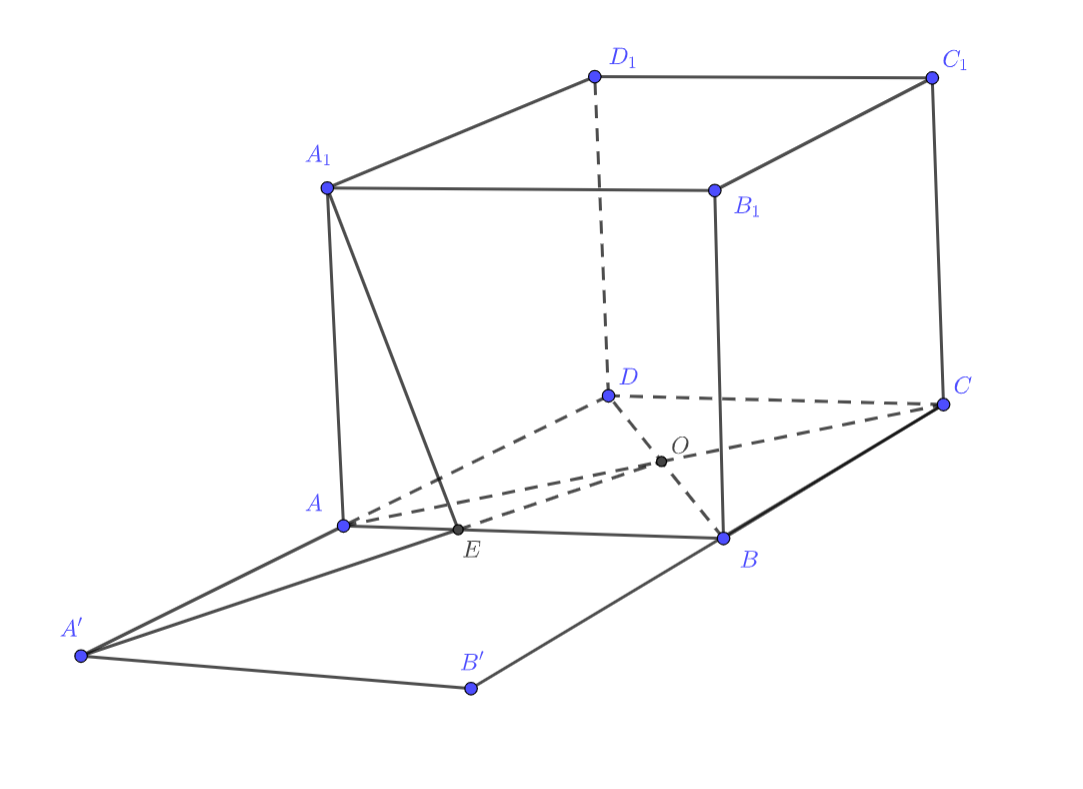
Рассмотрим и
. Тогда
для произвольной
(
получается
из
поворотом
на
относительно
). Но отсюда нам надо найти минимум
, который достигается только при
и будет равен
, то есть
Ошибка.
Попробуйте повторить позже
Рассмотрим всевозможные тетраэдры , в которых
. Каждый такой тетраэдр впишем в
цилиндр так, чтобы все вершины оказались на его боковой поверхности, причём ребро
было параллельно оси цилиндра. Выберем
тетраэдр, для которого радиус цилиндра - наименьший из полученных. Какие значения может принимать длина
в таком
тетраэдре?
![]()
Пусть - середина
и
- медианы равнобедренных треугольников
и
, a значит, биссектрисы и высоты. То есть
. Значит, отрезок
перпендикулярен плоскости
, следовательно,
. Таким образом,
лежит в
плоскости, перпендикулярной оси цилиндра (обозначим эту плоскость через
). Сечение цилиндра этой плоскостью - окружность, а
является хордой этой окружности. Тогда радиус цилиндра минимален, если
диаметр. Отметим, что это возможно в силу
того, что отрезки
и
длиннее, чем
. Действительно, из треугольников
и
следует, что
.
Рассмотрим тетраэдр, в котором является диаметром цилиндра. Возможны 2 случая: точки
и
лежат по одну (этот случай
представлен выше) или по разные стороны плоскости
.
Пусть - проекция точек
и
на плоскость
. Угол
, так как он вписан в окружность и опирается на её диаметр.
в силу равенства треугольников
и
. Тогда
. По теореме Пифагора в прямоугольных
треугольниках
и
соответственно:
.
Тогда, если точки и
лежат по одну сторону от плоскости
, то
. Если точки
и
лежат по
разные стороны от плоскости
, то
.
Доказано, что 𝐴𝐵 – диаметр цилиндра наименьшего радиуса – 2 балла; если при этом не проверено, что точки 𝐶 и 𝐷 могут лежать на боковой поверхности такого цилиндра (например, можно доказать, что треугольники 𝐴𝐵𝐶 и 𝐴𝐵𝐷 остроугольные; можно сделать, как в решении), то 1 балл вместо 2;
найдены оба значения 𝐶𝐷 – 3 балла;
найдено только одно значение 𝐶𝐷 – 1 балл вместо 3.
Ошибка.
Попробуйте повторить позже
Отрезок пересекает плоскость
под углом
и делится этой плоскостью в отношении
. Найдите радиус сферы,
проходящей через точки
и
и пересекающей плоскость
по окружности наименьшего радиуса.
Источники:
Обозначив точку пересечения с плоскостью
через
, получим
. В пересечении сферы с плоскостью получается
некоторая окружность. Проведём через
диаметр
этой окружности. Тогда
и
— хорды сферы, и по
свойству пересекающихся хорд:
. Так как
, то минимальный
радиус окружности больше или равен
и значение
достигается при
, то есть
центр этой
окружности. Так как
, то
При этом
Значит,
Ошибка.
Попробуйте повторить позже
Боковые рёбра ,
и
треугольной пирамиды
взаимно перпендикулярны. Точка
лежит на основании пирамиды
на расстоянии
от ребра
, на расстоянии
от ребра
и на расстоянии
от ребра
Какое наименьшее
значение может иметь объём пирамиды
при этих условиях?
Источники:
Опустим перпендикуляры из точки
на плоскости
и
соответственно. Обозначим
,
,
Согласно условию составим систему уравнений
Отсюда находим ,
,
Обозначим длины рёбер
,
и
через
и
соответственно.
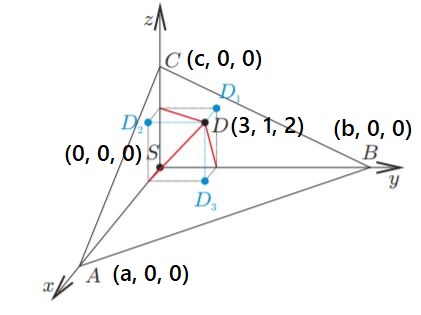
Лемма:
Доказательство: Введём систему координат с началом в точке как на рисунке. Запишем уравнение плоскости
.
Так как плоскость не проходит через начало координат, то . Значит можно поделить на
. Получим:
Теперь поставим в уравнение плоскости точки, в ней лежащие, чтобы найти коэффициенты ,
,
. Итого получим, что
,
,
. А значит уравнение плоскости
Подставив туда координаты принадлежащей этой плоскости точки , получим
Лемма доказана.
Из неравенства между средним арифметическим и средним геометрическим для трёх переменных получаем:
причём равенство имеет место при Объём пирамиды
поэтому
Равенство имеет место при
,
,
Ошибка.
Попробуйте повторить позже
В прямоугольном параллелепипеде с рёбрами
и
проведены два сечения – плоскостью,
проходящей через диагональ
, и плоскостью, проходящей через диагональ
. Найдите наибольшее возможное значение суммы
площадей поверхностей многогранников, на которые эти сечения разбивают данный параллелепипед.
Источники:
Подсказка 1
Нарисуйте картинку и попробуйте понять: что точно, вне зависимости от положения сечений будет содержаться в искомой сумме? Можем ли мы как-то избежать попадания в эту сумму какой-то части исходного параллелепипеда? А сколько раз туда попадут части наших сечений?
Подсказка 2
Итак, получается, что как бы ни были расположены сечения, их площади дважды войдут в искомые площади поверхностей. Значит надо эти площади максимизировать!
Подсказка 3
Какой фигурой будет являться каждое сечение? Как площади сечений связаны с длинами диагоналей? Исследуйте, где должны быть расположены вершины параллелограмма-сечения, чтобы расстояние до диагонали параллелепипеда было наибольшим.
Подсказка 4
Осталось лишь посчитать все нужные длины, призвав на помощь теорему Пифагора. Будьте внимательны к арифметике и задача окажется убита!
Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед сечениями, равна сумме площади поверхности параллелепипеда и площадей внутренних поверхностей. Сумма площадей внутренних поверхностей равна удвоенной сумме площадей сечений.
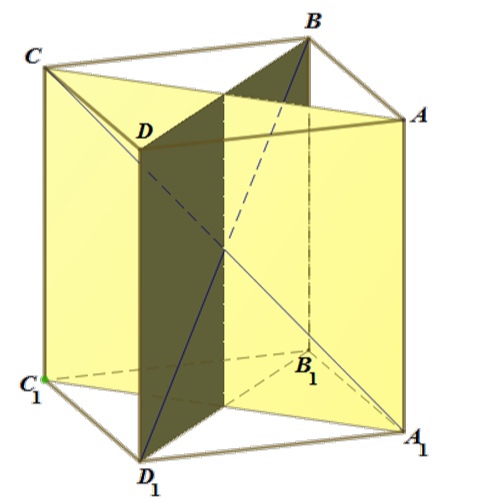
Найдем наибольшую возможную площадь сечения, проходящего через диагональ произвольного параллелепипеда с
ребрами
. Сечением является параллелограмм
, вершины которого лежат на противоположных рёбрах
параллелепипеда. Площадь параллелограмма равна произведению длины диагонали
на расстояние от точки
до
.
Рассмотрим проекцию параллелепипеда на плоскость, перпендикулярную диагонали . На рисунке видно, что расстояние от точки
ломаной
до точки
, то есть до диагонали
, наибольшее, если
совпадает с одной из вершин
или
.
Значит, сечение проходит через одно из ребер параллелепипеда. Таким образом, наибольшую площадь имеет одно из диагональных сечений. Все эти сечения являются прямоугольниками. Найдем наибольшую из их площадей
Из условия следует, что,
, и
. Поэтому
и
. Значит,
наибольшую площадь имеет сечение, проходящее через наибольшее ребро. По условию наибольшую длину имеет ребро
, значит,
наибольшую площадь
имеют сечения
и
.
Сумма площадей поверхностей многогранников, на которые разбивается параллелепипед этими сечениями (см. рисунок), равна
Ошибка.
Попробуйте повторить позже
В треугольной пирамиде рёбра
не длиннее, чем
и
соответственно, а площади граней
не
меньше, чем
и
соответственно. Найдите объём пирамиды
Источники:
Подсказка 1
Какой самый доступный способ отыскать площадь треугольника-грани, когда известны две его стороны? Сразу же напрашивается формула S = 0.5 * a * b * sin(γ). Оценим тогда площадь грани SAB: они никак не больше чем полупроизведение SA * SB * sin(∠ASB), причём синус также может принимать далеко не бесконечно большие значения.
Подсказка 2
Если всё сделано верно, то мы обнаружим, что верхняя и нижняя границы для площади грани SAB совпадают. А значит...?
Подсказка 3
Итак, теперь мы знаем SA, SB и ∠SAB. Проделайте аналогичную процедуру с другими бок. гранями, чтобы найти ещё рёбро и уголочки. Тогда мы узнаем и высоту пирамиды. Осталось подставить всё это в формулу объёма и радоваться результату!
Площадь боковой грани , по условию, не меньше
С другой стороны, она равна
Следовательно, , т.е.
перпендикулярно
. Аналогично получаем, что
и
перпендикулярно
и
. Поэтому объём пирамиды равен
Ошибка.
Попробуйте повторить позже
Пять рёбер тетраэдра имеют длины и
Определите, может ли при этом длина шестого ребра:
a) равняться
б) равняться
Источники:
(a) У нас есть 2 грани со стороной 2, но вместе с 2 треугольник может образовать только 4 и 5?!
(b) У нас есть 2 грани со стороной 2. Вместе с 2 треугольник может образовать только 4 и 5 или 11,1 и 13. Значит противоположная
сторона равна 9. Пусть нам дан тетраэдр и
,
,
. Тогда
и по неравенству треугольника для
сторона
. Значит последняя сторона
. По формуле Герона площадь
равна
. Тогда если
высота в этом треугольнике, то
. По теореме Пифагора
и
. Отсюда
следует, что
лежит на отрезке
Аналогично, , высота
в этом треугольнике длиной
,
,
Значит,
лежит на луче
за точку
. Отсюда
Вспомним, что у нас есть такое неравенство на
Оно выводится так: спроецируем всё на плоскость, перпендикулярную пусть
— проекция
,
— проекция
,
—
проекция
и
. Так как
и
перпендикулярны
, то
и
Значит, проекция
на эту
плоскость длиной от
до
, а проекция на прямую
это
Значит,
Подставим числа и получится, что так как , а
, то
а) нет
б) нет
Ошибка.
Попробуйте повторить позже
Радиус сферы, вписанной в правильную треугольную пирамиду, равен . Найдите величину двугранного угла при боковом ребре этой
пирамиды, при котором максимален объём другой пирамиды, вершинами которой служат центр вписанной в исходную пирамиду сферы и
точки касания этой сферы с боковыми гранями исходной пирамиды.
Источники:
Пусть у некоторой правильной пирамиды известно боковое ребро . Давайте посчитаем при какой дине стороны основания
пирамиды
будет обладать наибольшим объемом.
Теперь это функция от
. Возьмем производную по
. Она зануляется при
и в этой точке производная меняет свой знак
с + на -. Значит это точка максимума и объем максимальный при
.
Вернемся к задаче. Пирамида, вершинами которой служат точки касания и центр сферы, является правильной треугольной
пирамидой с ребром . Значит, чтобы объем был максимальным, нужно добиться того, чтобы сторона ее основания была
.
Из точек и
проведем перпендикуляры к
, в силу симметрии они попадут в одну точку
.
По доказанному ранее и при этом
. Значит
, но тогда угол
прямой, а его нам и нужно
было найти.
Ошибка.
Попробуйте повторить позже
Высота правильной треугольной пирамиды, проведенная из вершины основания к противоположной боковой грани, равна 4. Какие значения может принимать площадь полной поверхности такой пирамиды?
Источники:
Пусть высоты из вершины
на грань
, а
из вершины
на грань
. Тогда так как тетраэдр правильный, то
и
пересекаются на стороне
в tt середине
. Пусть
. Тогда
Поскольку равносторонний, то
.
Так как , то
Функция достигает максимуму при
и может быть бесконечно близко к 0, поэтому площадь может
быть в интервале
.



