Ошибка.
Попробуйте повторить позже
Кощей придумал для Ивана-дурака испытание. Он дал Ивану волшебную дудочку, на которой можно играть только две ноты — до и си. Для
прохождения испытания Ивану нужно сыграть какую-нибудь мелодию из 300 нот на свой выбор. Но до того, как он начнёт играть, Кощей
выбирает и объявляет запретными одну мелодию из пяти нот, одну — из шести нот, , одну — из 30 нот. Если в какой-то момент последние
сыгранные ноты образуют одну из запретных мелодий, дудочка перестаёт звучать. Сможет ли Иван пройти испытание, какие бы мелодии
Кощей ни объявил запретными?
Первое решение.
Рассмотрим всевозможные мелодии из нот до и си длины , коих
штук. Каждую такую мелодию периодически продолжим в обе
стороны, получив бесконечную в обе сторону мелодию. Назовём две получившиеся бесконечные мелодии эквивалентными, если одна
получается из другой сдвигом.
Наименьший период всех бесконечных мелодий, кроме двух, состоящих только из нот до и только из нот си, равен Количество не
эквивалентных друг другу бесконечных мелодий равно
(каждой бесконечной мелодии периода
эквиваленты
мелодий (включая саму
с периодом, который будет циклическим
сдвигом
нот, дающих мелодию
)
Из них мелодий, содержащих запрещённые Кощеем мелодии, не больше
(в скобках учтены запретные мелодии длины , полученные дописыванием
символов к запретной мелодии длины
, а за
скобками — все остальные).
Таким образом, найдётся бесконечная мелодия, которая не содержит запретных мелодий, и для прохождения испытания Ивану
достаточно сыграть её кусок длины
______________________________________________________________________________________________________________________________________________________
Второе решение.
Пусть - число мелодий длины
, не содержащих запретных последовательностей нот. Будем считать, что
По индукции
докажем, что
для всех натуральных
.
База индукции
Предположим, что неравенство верно для всех
, меньших
Покажем, что тогда
Заметим,
что
Действительно, мы можем добавить в конец ноту двумя способами к уже имеющейся незапрещенной мелодии из нот. При добавлении
ноты могла возникнуть запретная мелодия длины
в конце последовательности, однако она "испортит"максимум
последовательности нот, так как первые
ноты до "запрещенной"мелодии - незапрещенная мелодия длины
. Аналогично могли
получить запретную последовательность из
нот и испортить разрешённую мелодию из
нот и т. д. (Здесь мы можем вычесть
лишнее, если
, и часть вычитаемых мелодий могут быть одинаковыми, но поскольку мы пишем оценку снизу, всё
правильно.)
Из предположения индукции для
также следуют неравенства:
Применим эти следствия, а также неравенство выше, для доказательства перехода индукции и получим:
Следовательно, и переход доказан.
Тогда из-за положительности последовательность
возрастающая, а значит
, откуда следует, что Иван справится с
испытанием Кощея.
Ошибка.
Попробуйте повторить позже
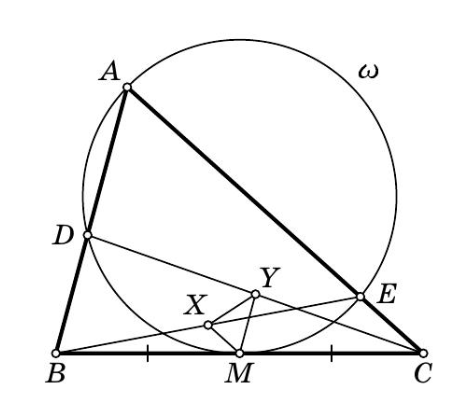
Точка — середина стороны
треугольника
Окружность
проходит через точку
касается прямой
в точке
и
пересекает сторону
в точке
а сторону
— в точке
Пусть
и
— середины отрезков
и
соответственно.
Докажите, что окружность, описанная около треугольника
касается
Источники:
Подсказка 1
У нас есть с вами сразу три середины каких-то отрезков. Понятно, что можно тогда где-то найти средние линии и параллельности) Что из этого получится?
Подсказка 2
Из этого можем получить, что ∠XMY = ∠A. Теперь подумайте: что значит, что окружности будут касаться? Скорее всего, вы понимаете даже, где. Какое условие там будет выполнено?
Подсказка 3
Хочется, чтобы они касались в точке M, то есть нужно, чтобы описанная около XMY окружность касалась BC в точке M. То есть, ∠YMC = ∠YXM. А мы знаем, что ∠YMC = ∠ABC. По факту что нам достаточно теперь доказать?
Подсказка 4
Из знания уже одного угла нам достаточно доказать, что XMY подобен треугольнику ABC! Для этого попробуйте использовать то, что это средние линии, а нужные удвоенные отрезки можно выразить с помощью теорем о касательной и секущей :)
Заметим, что и
— средние линии треугольников
и
поэтому
и
Тогда
По свойству касательной и секущей к окружности имеем откуда
Аналогично получаем
Деля одно на другое и пользуясь тем, что находим
Получаем, что треугольники и
подобны по углу и отношению прилежащих сторон.
Тогда Получается, что в описанной окружности треугольника
угол, опирающийся на хорду
равен углу между хордой
и прямой
Это значит, что прямая
касается окружности, описанной вокруг треугольника
Следовательно, рассматриваемые окружности касаются.
Ошибка.
Попробуйте повторить позже
Петя подсчитал количество всех возможных -буквенных слов, в записи которых могут использоваться только четыре буквы
и
причём в каждом слове букв
и
поровну. Вася подсчитал количество всех возможных
-буквенных слов, в записи которых
могут использоваться только две буквы
и
и в каждом слове этих букв поровну. У кого слов получилось больше? (Слово — это любая
последовательность букв.)
Источники:
Установим взаимно-однозначное соответствие между словами Пети и Васи. Разобьём Васино слово из букв на блоки из двух букв.
Заменим каждый блок
на букву
блок
— на букву
блок
— на букву
и блок
— на букву
Получится слово
из
букв, в котором букв
и
поровну (изначально их было поровну, замена блоков
и
убирает равное число букв
и
а значит, и блоков
будет столько же, сколько блоков
). Итак, каждому слову Васи мы сопоставили слово
Пети.
Наоборот, по каждому -буквенному слову Пети легко восстановить, из какого слова Васи оно получилось по описанному выше
правилу: надо заменить буквы по тому же правилу.
Поровну
Ошибка.
Попробуйте повторить позже
Две окружности пересекаются в точках и
Их общая касательная (та, которая ближе к точке
) касается окружностей в точках
и
Прямая
пересекает прямую
в точке
На продолжении
за точку
выбрана точка
так, что
Прямая
вторично пересекает окружность, содержащую точку
в точке
Прямая
вторично пересекает окружность, содержащую точку
в точке
Докажите, что точки
и
лежат на одной
прямой.
Источники:
![]()
Рассматривая первую окружность и степень точки относительно нее получим, что
Аналогично, для второй
окружности:
откуда
Так как
получаем что
откуда четырехугольник
вписанный. Рассмотрим инверсию с центром в точке
переводящую точку
в точку
Рассматривая степень точки
относительно первой и второй окружности получим, что
Получается, что та же инверсия переводит точку
в точку
и
в
Поскольку точки
лежат на окружности, проходящей через центр инверсии, их образы лежат на одной
прямой, что и требовалось доказать.
Ошибка.
Попробуйте повторить позже
В классе ученика. Было организовано
кружка, причём каждый кружок состоит из трёх человек и никакие два кружка не совпадают
по составу. Докажите, что найдутся такие два кружка, которые пересекаются ровно по одному ученику.
Источники:
Решим более общую задачу: пусть учеников занимаются в
кружках (из трёх человек),
Предположим противное: каждые два
кружка либо не пересекаются, либо пересекаются ровно по двум ученикам. Заметим, что если кружки
и
пересекаются с кружком M,
то они пересекаются и между собой (их пересечения с
имеют общий элемент). Значит, кружки разбиваются на группы пересекающихся
между собой кружков. Каждой группе кружков соответствует группа учеников — объединение их составов. Эти группы также не
пересекаются. Далее можно рассуждать по-разному.
Первый способ. Поскольку кружков больше, чем учеников, в какой-то группе это неравенство также сохраняется. Поставим в
соответствие каждой паре кружков этой группы пару учеников, каждый из которых ходит ровно в один из этих кружков. Пар кружков
больше, чем пар учеников, поэтому какой-то паре учеников соответствует по крайней мере две пары кружков
и
Но кружки
и
не могут иметь двух общих учеников, поскольку пары
и
не совпадают.
Противоречие.
Второй способ. Если в группе, содержащей некоторый кружок есть кружки, содержащие хотя бы две из трех пар
скажем кружок
и кружок
то
(два последних кружка должны иметь двух общих членов).
Единственный возможный кружок, пересекающийся с каждым из этих трех по двум элементам, — это
Таким образом, в такой
группе не более четырёх кружков, куда ходят не менее четырёх учеников. Если же все кружки группы содержат только
одну из трёх указанных пар (например,
), то количество кружков в ней на
меньше количества всех учеников, их
посещающих.
Итак, число кружков не превосходит числа учеников в классе.



