Ошибка.
Попробуйте повторить позже
Коническое (пожарное) ведро было заполнено водой до самого края.

В него положили шар, причем он полностью покрылся водой. Покажите, что при этом из ведра вылилось не более половины бывшей там воды.
Источники:
Подсказка 1
Если мы хотим доказать, что что-то меньше чего-то, то нам надо взять это что-то максимальным, а после этого доказать, что даже в этом случае выполняется требуемое. Шар у нас лежит не выше уровня воды, при этом, он касается поверхности конуса. В какой ситуации тогда радиус шара будет максимальным(ну а значит и его объем)?
Подсказка 2
Предельное положение - это когда шар вписан в конус. А значит, окружность радиуса такого же как у шара вписана в сечение конуса, которое проходит через диаметр окружности в основании и вершину. Значит, мы можем взять за r - радиус шара, за h - высоту конуса и за R - радиус окружности в основании конуса и тогда картинка однозначно фиксируется и все через все выражается. Сделайте это и поймите связь между r и парой h и R. Чему тогда равно отношение объемов(ведь этого от нас и просят)?
Подсказка 3
Отношение объемов равно, в силу того, что (h - r)/r = sqrt(h^2 + R^2)/r, 4 * (h / r) * (1 - 2 * (h/r)). Мы хотим максимизировать объем, значит, надо взять максимум у этой параболы(у нас же относительно h/r - выражение представляется графически параболой), а она не больше 1/2.
Обозначим радиус шара через радиус основания конуса через
а высоту конуса — через
Тогда объём конуса
равен
Объём шара
Отношение этих объемов равно
Можно считать, что верхняя точка шара находится на поверхности воды, иначе воды выльется ещё меньше.
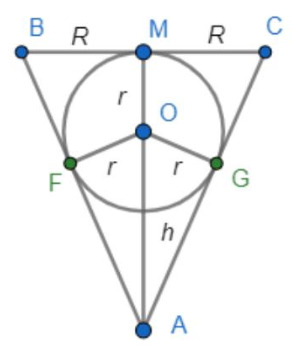
Из подобия прямоугольных треугольников и
имеем
Возведем равенство в квадрат, получим
Значит, отношение объёмов равно
где Максимум этой функции достигается в вершине параболы, то есть при
и составляет
Заметим, что максимум достигается при при этом
Ошибка.
Попробуйте повторить позже
Многогранник изображен в ортогональной проекции на плоскость
![]()
Докажите, что такой многогранник невозможен.
Источники:
Подсказка 1
У нас на картинке дополнительно нарисованы точки пересечения A₂, B₂, C₂ и D₂. Что их всех связывает?
Подсказка 2
Они получены как пересечение прямых из плоскости ABCD и прямых из плоскости A₁B₁C₁D₁. Тогда где должны лежать все эти точки?
Подсказка 3
На общей для этих плоскостей прямой! А теперь внимательно смотрим на рисунок)
![]()
Прямые и
пересекаются в точке
, лежащей в обеих плоскостях,
и
, то есть на их общей прямой. То же
верно для точек
получающихся как пересечения одноименных рёбер. Значит, все эти точки должны лежать на одной прямой,
что не выполняется.
Если зафиксировать, например, точки , то можно построить изображение вершины
(на рисунке это точка
, которое
не совпадает с изображением точки
на проекции.



