Ошибка.
Попробуйте повторить позже
Точки лежат в вершинах клеток клетчатой бумаги. Может ли угол
оказаться равным
Источники:
Подсказка 1
Угол может располагаться вообще как угодно, неприятно. Давайте использовать линии сетки. Проведём из точки В луч горизонтальный и опустим на него перпендикуляры АЕ и СF, получим углы α = АВЕ и β = CBF (возможно, какой-то из них нулевой! если Е или F на одной линии с В). Что мы можем найти для этих углов?
Подсказка 2
Можем найти тангенс α и β. Теперь давайте вычислим тангенс АВС с помощью формулы тангенса суммы. Поразмышляйте над полученным выражением: что же нам даёт расположение точек в узлах сетки... давайте, не ленитесь, не хочу лишать Вас удовольствия
Подсказка 3
Оп-па, а это выражение (тангенс суммы) рационален! А тангенс 30 градусов нет. Развалили задачу
Проведем из точки луч по линии сетки:
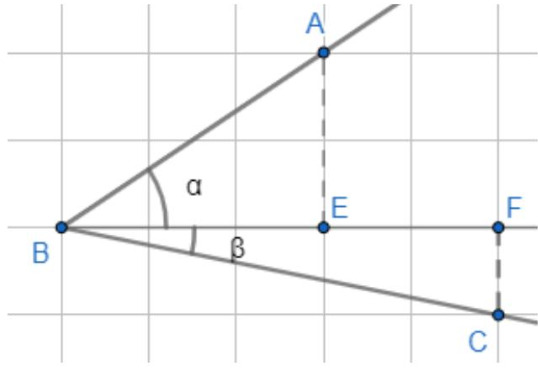
Тогда угол будет равен сумме углов
и
(они могут быть и отрицательными). Тангенс такого угла равен отношению двух
целых чисел, то есть является рациональным числом. Тогда
также рациональное число. Но — число иррациональное.
Если один из углов и
является прямым, то можно использовать луч, идущий перпендикулярно первому.
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике провели высоту
медиану
и биссектрису
Точки
и
— ортогональные
проекции вершин
и
на прямую
Докажите, что точки
и
лежат на одной окружности.
Источники:
Подсказка 1
Давайте для начала попробуем продлить биссектрису до пересечения с описанной окружностью ABC в точке X. Что теперь можно вспомнить про эту точку?
Рассмотрим без ограничения общности Тогда точка
лежит внутри треугольника
, а точка
вне
его.
Первое решение.
Построим описанную окружность треугольника , тогда продолжение биссектрисы
пересечет ее в точке
,
являющейся серединой дуги
. Тогда
, то есть медиана
равнобедренного треугольника
будет также и
высотой.
![]()
Так как , то получим, что
. Так как
аналогично получаем, что
.
Но углы равны, как вписанные углы, опирающиеся на одну дугу.
В итоге . Но из равенства углов
следует, что точки
лежат на одной
окружности.
Второе решение.
Обозначим через и
точки пересечения прямых
и
и
соответственно.
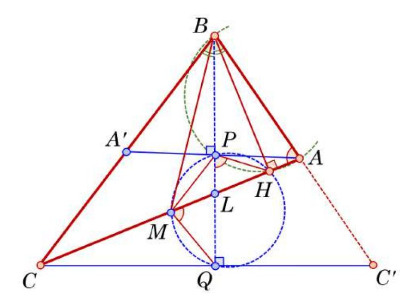
Поскольку — биссектриса и
треугольники
и
— равнобедренные, и значит,
и
В треугольнике точки
и
— середины сторон
и
поэтому
— средняя линия, и значит,
Аналогично,
Следовательно,
Возможны два случая:
a) Точки
и
лежат на одной окружности с диаметром
поэтому четырёхугольник
— вписанный.
Значит,
Следовательно, точки и
лежат на одной окружности.
б) тогда точки
и
лежат на одной окружности с диаметром
поэтому четырёхугольник
—
вписанный. Значит,
Следовательно, точки и
лежат на одной окружности.



