Отбор Иннополиса —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Отбор Иннополиса

Тема Иннополис (Innopolis Open)

Отбор Иннополиса

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела иннополис (innopolis open)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#78842

Из множества 1, 2, …, 10 выбираются равновероятно три числа (возможно одинаковых). Какова вероятность того, что сумма этих чисел равна 10?

Источники: Иннополис-2017, отборочный тур, 11 класс (см. olymp.innopolis.ru)

Подсказки к задаче

Подсказка 1

Сначала запишем условие в виде равенства, то есть у нас получится x+y+z=10 для каких-то чисел от 1 до 10. Давайте если не сталкивались с такой идеей, попробуем до неё дойти сами. Представим число 10 так, что как будто у нас есть 10 шаров. Что нам надо будет сделать тогда с ними, чтобы наше равенство было верным?

Подсказка 2

Верно, нужно как-то разделить шары на три кучки — это будет равносильно нашему равенству. Понятно, что в каждой кучке должен быть хотя бы один шар. Допустим, мы выложили шары в ряд и делим на кучки перегородками. Сколько тогда есть в принципе вариантов разбить на кучки?

Подсказка 3

Да, нам нужно из девяти мест, которые есть между шарами, выбрать два. И это будут как раз те варианты, когда наше равенство верно. Теперь осталось только посчитать общее число вариантов и найти вероятность. Победа!

Показать ответ и решение

Нужно найти, сколькими способами можно решить уравнение

x1+ x2+x3 =10

где $x1,x2,x3 ∈ 1,2 ...,10$

Выпишем в ряд десять единиц и поставим между ними две перегородки (в разные места). Тогда $x1$ это число единиц до левой перегородки, $x2$ — между левой и правой, $x3$ — после правой. Так как единиц всего $10$ , то $x1 +x2+ x3 = 10$ . Заметим, что мест для расположения перегородок всего $9$ , а нам нужно выбрать только $2$ . Поэтому число решений уравнения равно $C2 = 36. 9$ Всего есть $103$ способов выбрать $3$ числа из $10$ . Значит итоговая вероятность равна $-36-. 103$

Ответ: 0.036

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76054

Даны два многочлена

4 3 2 G(x)= x +Ax +Bx +Cx +D

и $H(x)= x2+Ax + B.$ Найдите значение $G(x1)+G (x2),$ где $x1,x2$ — корни многочлена $H (x).$

Показать ответ и решение

Заметим, что если вынести $x2$ в $G(x),$ то получим

2 2 2 G (x)= x ⋅(x + Ax +B)+ Cx +D = x ⋅H(x)+Cx +D

Следовательно, условие про $G(x1)+G(x2)$ примет вид:

2 2 G (x1)+ G(x2)= (x ⋅H (x1)+ Cx1+ D)+ (x ⋅H (x2)+ Cx2+ D)

Но, по условию, $x1,x2$ корни $H(x),$ следовательно,

G(x )+G (x )= C(x +x )+ 2D 1 2 1 2

Осталось применить теорему Виета для $H(x),$ чтобы найти $x1 +x2 :$

G(x1)+ G(x2)= C(x1+ x2)+ 2D =C ⋅(− A)+2D = 2D− AC

Ответ:

$2D − AC$

Ошибка.
Попробуйте повторить позже

Задача 3#68310

Вписанная окружность треугольника $ABC$ касается сторон $AB$ и $AC$ в точках $D$ и $E$ соответственно, а $O$ — центр описанной окружности треугольника $BCI.$ Докажите, что $∠ODB = ∠OEC.$

Источники: Иннополис-2017

Подсказки к задаче

Подсказка 1

Давайте подумаем про точку O. Она равноудалена от B, I и C (это ведь центр окружности)...А какая еще точка удовлетворяет этим условиям?)

Подсказка 2

По лемме о трезубце - это середина дуги BC! А т.к. это середина дуги, то углы OAB и OAC равны. Осталось найти еще равенство двух треугольничков, и задача решена)

Показать доказательство

$PIC$

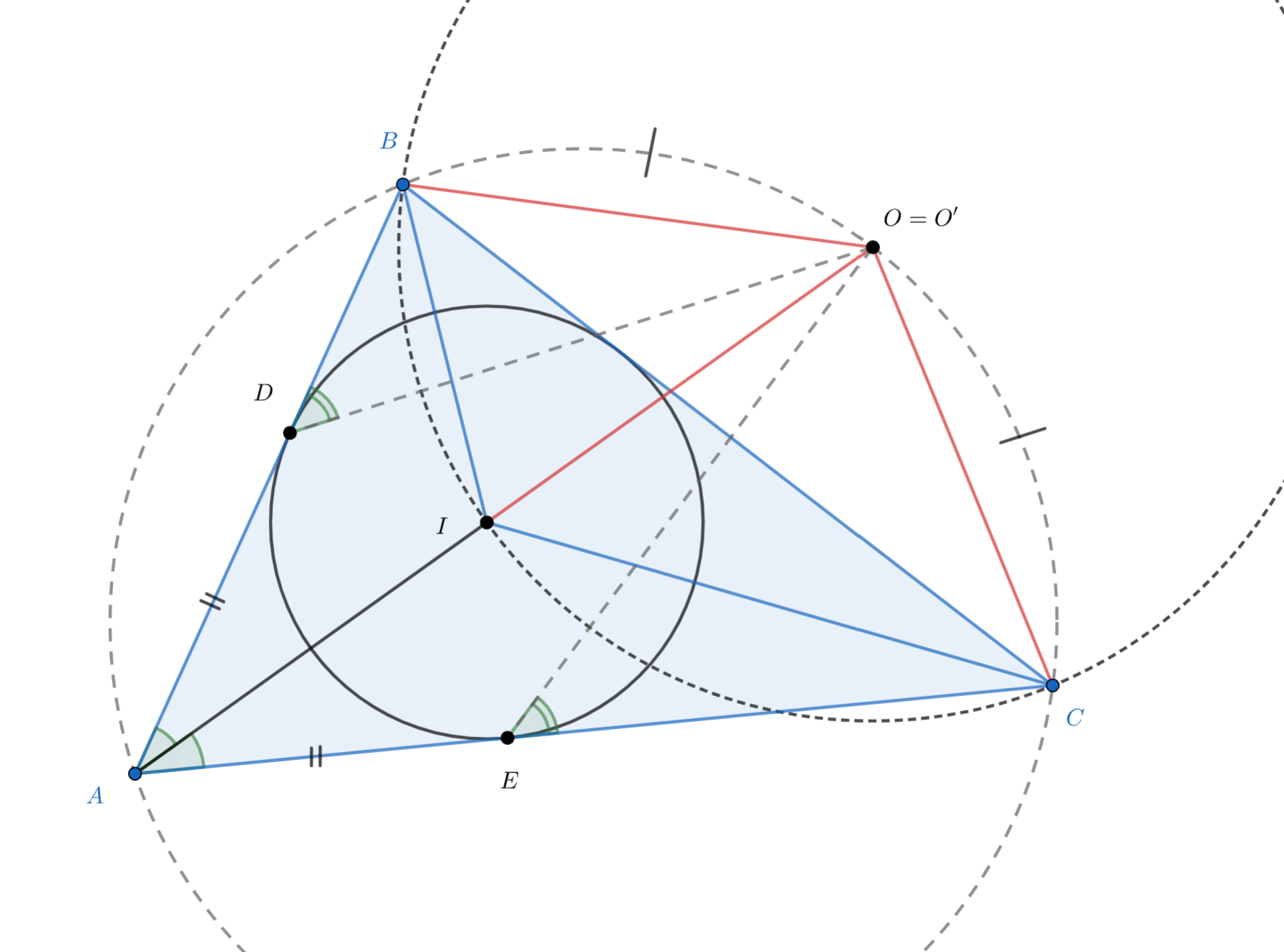
Рассмотрим точку $O′$ — середину дуги $BC$ (дуга не содержит точку $A$ ), описанной окружности треугольника $ABC$ . По лемме о трезубце получаем

O′C = O′B =O ′I

Следовательно, $′ O$ равноудалена от всех трех вершин треугольника $BIC$ , поэтому $′ O = O.$

Так как $O$ — середина дуги $BC$ , то $∠BAO = ∠CAO$ . К тому же $AD = AE$ как касательные, проведенные из одной точки $A$ . В итоге получаем, что треугольник $ADO$ равен треугольнику $AEO$ по двум сторонам и углу между ними. Но тогда $∠ODB = ∠OEC$ как внешние углы равных треугольников.