Планиметрия на Турломе —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Планиметрия на Турломе

Тема ТурЛом (турнир Ломоносова)

Планиметрия на Турломе

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела турлом (турнир ломоносова)

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#68033

Внутри окружности $ω$ проведены две перпендикулярные хорды, пересекающиеся в точке $P;$ точки $M 1$ и $M 2$ их середины. Прямая $M1M2$ пересекает $ω$ в точках $A$ и $B,$ причём $M1$ лежит между $A$ и $M2.$ Какие значения может принимать разность $BM2 − AM1,$ если $PM1 = 15,PM2 = 20?$

Источники: Турнир Ломоносова-2023, 11.3 (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Такс, у нас есть две хорды и их середины, есть еще и третья хорда, у которой мы тоже можем отметить середину! Какое доп.построение хочется сделать?

Подсказка 2

Да, мы знаем, что отрезок проведённый из центра окружности к середине хорды — перпендикулярен хорде, поэтому давайте проведём три таких отрезочка!(к каждой из хорд). Что можно сказать про полученный четырёхугольник OM₁PM₂, где O - центр окружности?

Подсказка 3

Верно, это прямоугольник! Тогда мы можем найти M₁M₂ из прямоугольного треугольника! Осталось понять, как от M₁M₂ прийти к исходной разности в вопросе задачи, учитывая, что M - середина AB!

Показать ответ и решение

$PIC$

Пусть $O −$ центр окружности, $M$ — середина отрезка $AB.$ Поскольку отрезок, соединяющий центр окружности с серединой хорды перпендикулярен этой хорде,

∠OM1P =∠OM2P =∠OMA = 90∘.

Заметим, что

BM2 − AM1 = (BM − MM2 )− (AM − MM1 ) =MM1 − MM2,

т.к. $AM = BM.$

Далее, в четырёхугольнике $OM1P M2$ три угла прямые, т.е. этот четырёхугольник — прямоугольник,

OM1 =P M2 = 20,OM2 = PM1 = 15,∠M1OM2 = 90∘.

Тогда в прямоугольном треугольнике $OM1M2$ проведена высота $OM$ на гипотенузу. По теореме Пифагора $∘ ---2----2- √ ------- M1M2 = OM 1 +OM 2 = 400 +225= 25.$ Так как катет есть среднее геометрическое гипотенузы и своей проекции на неё, то $MM1 =16,MM2 = 9.$ Откуда получаем ответ.

Ответ: 7

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#76578

Пусть $O$ — центр описанной окружности, $G$ — точка пересечения медиан остроугольного треугольника $ABC.$ Прямая, перпендикулярная $OG$ , проходящая через точку $G,$ пересекает отрезок $BC$ в точке $K.$ Касательная к описанной окружности треугольника $ABC$ в точке $A$ пересекает прямую $KG$ в точке $L.$ Найдите величину угла $∠ACB,$ если $∘ ∠LOK = 155 ,$ а $∘ ∠ABC =53 .$

Источники: Турнир Ломоносова-2022, 11.3

Подсказки к задаче

Подсказка 1

Нас просят найти какой-то угол и из условий нам дали значения каких-то углов. В таких задачах, где надо работать с углами, очень часто могут помочь вписанные четырёхугольники. Давайте попробуем найти такие, которые бы смогли перенести наши уголочки из условия в какие-то более удобные места.

Подсказка 2

Попробуйте посмотреть на GMKO и AOGL: они оба содержат части угла из условия LOK, а так же переносят их ближе к треугольнику AMC, а что мы можем сказать про угол ABC, можем ли мы его тоже перенести поближе к AMC?

Подсказка 3

Верно, ABC равен углу LAC, как угол между касательной и хордой, остаётся только внимательно присмотреться к треугольнику AMC и писать ответ.

Показать ответ и решение

Пусть $M$ — середина стороны $BC;$ поскольку $AM$ — медиана, то точки $G$ лежит на $AM.$

$PIC$

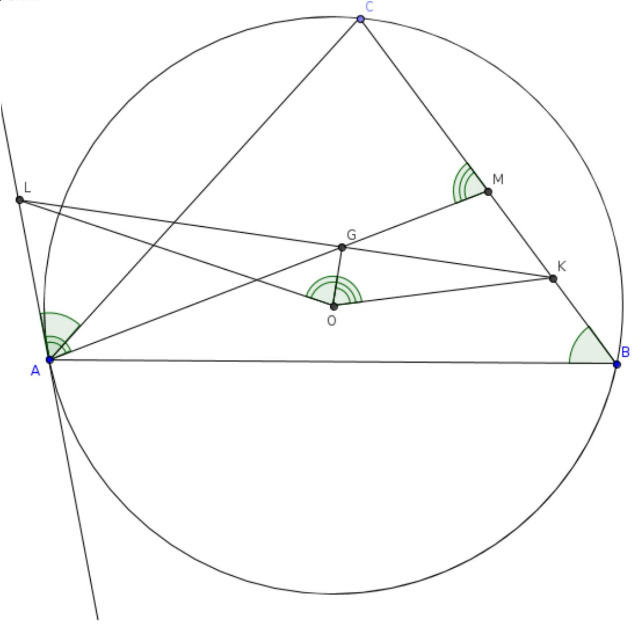
Четырёхугольник $OGMK$ — вписанный, так как $∠OGK =90∘ = ∠OMK$ (первое равенство по условию, второе следует из того, что $OM$ — серединный перпендикуляр к $BC$ ), откуда $∠GOK = 180∘ − ∠GMK =$ $∠GMC.$

Четырёхугольник $OGLA$ — вписанный, так как $∠OGL = 90∘ = ∠OAL$ (первое равенство по условию, второе следует из того, что $OA$ — радиус, а $AL$ — касательная к описанной окружности треугольника $ABC$ ), откуда $∠GOL =∠GAL.$

Значит,

∠ACB = 180∘− (∠CAM + ∠CMA )= 180∘ − (∠LAM + ∠CMA − ∠LAC )=

= 180∘− (∠LOG +∠GOK − ∠ABC )= 180∘ − (∠LOK − ∠ABC )=

= 180∘ − (155∘− 53∘) =78∘

Первое равенство следует из суммы углов треугольника $AMC.$

Ответ:

$78∘$

Ошибка.
Попробуйте повторить позже

Задача 3#67200

В выпуклом четырёхугольнике две противоположные стороны равны и перпендикулярны, а две другие равны $a$ и $b.$ Найдите его площадь.

Источники: Турнир Ломоносова-2016, отборочный тур (см. turlom.olimpiada.ru)

Подсказки к задаче

Подсказка 1

Когда в задачах по геометрии даны перпендикулярные прямые, но явно не обозначена точка их пересечения, то часто бывает, что нужно продлить прямые до их пересечения. Попробуйте сделать это и в нашей задаче. Какие фигуры получатся?

Подсказка 2

Правильно, получатся два прямоугольных треугольника — с гипотенузой, равной а, и с гипотенузой, равной b. Обозначьте неизвестные стороны какими-нибудь буквами, не забывая, что перпендикулярные стороны равны друг другу. Как теперь выразить площадь четырехугольника?

Подсказка 3

Верно, как разницу площадей этих прямоугольных треугольников! Теперь у нас есть формула для площади, но в ней всё ещё присутствуют неизвестные стороны. Значит, нужно найти, как ещё данные a и b из условия связаны c длинами неизвестных сторон. Какую теорему о прямоугольных прямоугольниках мы знаем?

Подсказка 4

Теорему Пифагора! Распишите теорему Пифагора для прямоугольных треугольников, немного преобразуйте и подставьте в формулу для площади!

Показать ответ и решение

Если $a =b,$ то получаем прямоугольник, у которого противоположные стороны параллельны, а не перпендикулярны.

Пусть для определённости дальше $b> a.$ Если $a> b,$ то нужно будет в ответе поменять буквы местами, поэтому учтём это знаком модуля.

Первое решение.

$PIC$

Обозначим длину двух равных сторон через $x$ . Продолжим их до пересечения и обозначим длины двух получившихся коротких отрезков через $y$ и $z.$ Площадь $S$ исходного четырёхугольника есть разность площадей двух прямоугольных треугольников: с катетами $x +y$ и $x+ z$ и с катетами $y$ и $z$ . Поэтому

2S = (x+ y)(x+ z)− yz = x2+xy +xz

По теореме Пифагора

y2+ z2 =a2,(x +y)2+ (x+ z)2 =b2

Поэтому

2 2 2 b− a = 2x +2xy+ 2xz = 4

В итоге площадь многоугольника равна

b2− a2 4

Второе решение.

$PIC$

Из четырёх таких многоугольников можно сложить квадрат со стороной $b,$ из которого вырезан квадрат со стороной $a.$ Поэтому площадь одного многоугольника равна $14(b2 − a2).$