Проведём через пару скрещивающихся рёбер тетраэдра две параллельные плоскости. Так же поступим для двух других пар скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани — прямоугольники, и параллелепипед прямоугольный. Пусть — его центр, являющийся также центром описанной сферы тетраэдра Пусть также — точки, симметричные соответственно относительно точки Докажем, что все построенные прямые проходят через точку

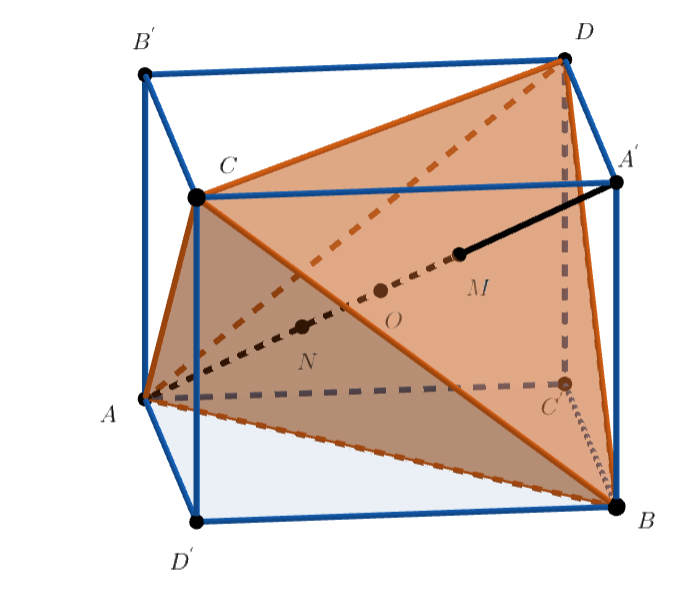
Пусть — центр масс треугольника . Тогда

То есть точка лежит на диагонали и делит её в отношении , считая от вершины Аналогично центр масс треугольника лежит на этой диагонали и делит её в отношении , считая от вершины Точка — середина отрезка поэтому

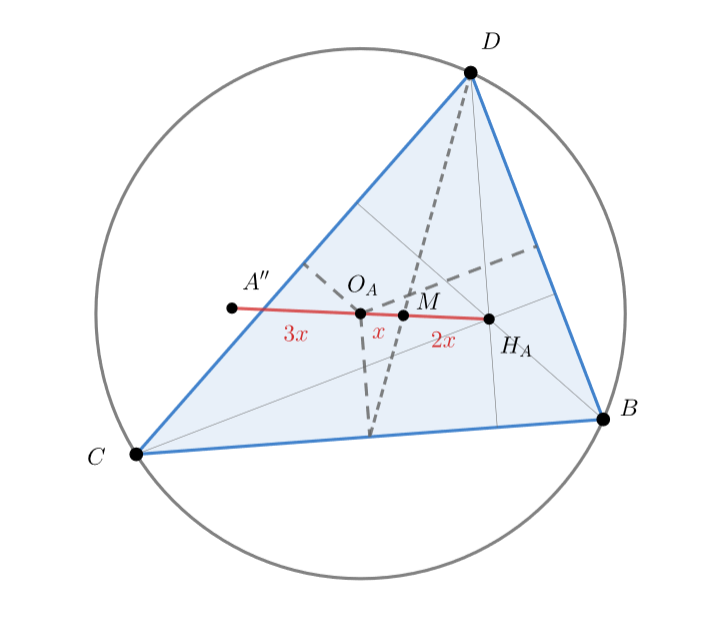
Рассмотрим проекцию на плоскость — проекция точки , — проекция центра Точка совпадает с центром описанной сферы тетраэдра поэтому — центр описанной окружности треугольника

Тогда прямая проецируется в прямую Эйлера треугольника Пусть Тогда ( делит отрезок в отношении , это отношение сохраняется при проецировании). Кроме того, лежат на одной прямой и (прямая Эйлера), отсюда Следовательно, , а прямая , перпендикулярная плоскости , делит отрезок пополам, а значит, совпадает с прямой . Итак, все построенные прямые проходят через точку .

Прямые и пересекаются в точке , лежащей в обеих плоскостях, и , то есть на их общей прямой. То же верно для точек получающихся как пересечения одноименных рёбер. Значит, все эти точки должны лежать на одной прямой, что не выполняется.

Если зафиксировать, например, точки , то можно построить изображение вершины (на рисунке это точка , которое не совпадает с изображением точки на проекции.

Обозначим через точку пересечения боковых сторон трапеции Тогда точка является центром гомотетии с положительным коэффициентом, переводящей отрезок в отрезок По теореме о трех центрах гомотетии (теорема о трёх колпаках) точки лежат на одной прямой. Обозначим эту прямую через и докажем, что все такие прямые лежат в одной плоскости.

Для этого будем последовательно рисовать их. Сначала проведем прямые и они лежат в одной плоскости т.к. пересекаются в точке Прямая пересекает в точке а прямую — в точке поэтому она также лежит в плоскости Наконец, прямая пересекает прямую в точке а прямую — в точке так что и она лежит в плоскости

Итак, все четыре прямые лежат в одной плоскости, и в ней же лежат все шесть точек что и требовалось доказать.

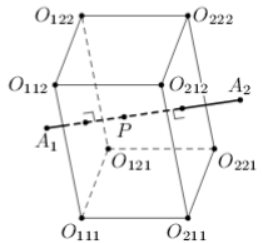
Будем называть ГМТ серединным перпендикуляром к отрезку . Пусть — серединный перпендикуляр к отрезку . Тогда (поскольку на каждой такой сфере лежат обе точки ). Легко видеть, что , поскольку обе перпендикулярны прямой . Аналогично определим плоскости для и для . Поскольку шесть выбранных плоскостей попарно параллельны, то они образуют параллелепипед, осталось заметить, что его вершинами будут точки . Действительно, каждая точка лежит в плоскостях (например), откуда и следует нужное. Учитывая, что диагонали параллелепипеда пересекаются в одной точке, всё доказано.

Пусть эта пирамида . Биссекторы, содержащие рёбра , пересекаются в одной точке , которая находится на одинаковом расстоянии от всех четырёх граней, то есть является центром вписанной в пирамиду сферы. Если нашлась ещё одна сфера с центром , то она также обязана лежать в пересечении трёх биссекторов, но такая точка всего одна, поэтому сфера единственная.

Заметим, что точки лежат и на сфере с центром в точке и в одной плоскости. Следовательно, они лежат на окружности являющейся пересечением сферы с плоскостью. Пусть — центр этой окружности. Тогда перпендикулярно плоскости основания и любая точка на прямой равноудалена от всех точек окружности Поэтому на найдётся и такая точка для которой Тогда на сфере с центром в точке и радиусом лежат все вершины пирамиды, а также все окружности

Следовательно, на этой сфере лежат все точки и Пусть — точка на сфере диаметрально противоположная точке Покажем, что описанные окружности треугольников проходят через точку Поскольку точки и лежат на сфере, достаточно проверить, что они лежат на сфере, достаточно в одной плоскости. Эта плоскость перпендикулярна прямой и проходит через точку В самом деле, поскольку они опирается на диаметр сферы и поскольку они опираются на диаметры и описанных окружностей треугольников и

Пусть дан тетраэдр а — середины ребер и соответственно. Тогда прямые и параллельны как средние линии треугольников и а прямые и параллельны как средние линии треугольников и Отсюда немедленно следует, что — параллелограмм. Но все его вершины лежат на сфере, поэтому он вписанный, т. е. — прямоугольник. В силу параллельности сторонам прямоугольника прямые и перпендикулярны. Аналогично и

Докажем, что перпендикулярность противоположных сторон тетраэдра является достаточным условием того, что высоты тетраэдра пересекаются в одной точке. Построим плоскость, проходящую через ребро перпендикулярно Высоты тетраэдра, опущенные из точек и лежат в этой плоскости, и значит, пересекаются. Обозначим точку их пересечения через Высоты из вершин и также должны пересекать высоты из вершин и но так как они не лежат в плоскости пересекать их они могут только в точке

 Применим теорему о трех перпендикулярах. В силу того, что и , получим, что проекция на плоскость перпендикулярна , то есть

Заметим, что середина гипотенузы - точка это центр описанной окружности прямоугольного треугольника . Аналогично середина гипотенузы - точка - центр описанной окружности прямоугольного треугольника . Тогда если провести перпендикуляр к плоскости в точке и перпендикуляр к плоскости в точке , то центр описанной окружности пирамиды - точка пересечения этих перпендикуляров. Но перпендикуляр к плоскости в точке совпадает с прямой . То есть точка и есть точка .

При этом на прямой (перпендикуляр к плоскости в точке ) будут лежать все в силу того, что - ГМТ точек равноудаленных от

То есть точка - центр треугольной пирамиды - опять-таки должна лежать на прямой

Хотелось бы добиться того, чтобы ( по очевидным причинам). Но тогда . То есть середина гипотенузы равноудалена от точек . Так же точка равноудалена от точек . Но тогда должен быть ромбом, при этом его диагональ должна быть равна стороне. Понятно, что тогда . Значит, что , то есть

Если точка сама находится на расстоянии от , то подойдёт вся плоскость , (то есть любая прямая . Если расстояние , то таких прямых нет. Иначе это прямая, которая касается цилиндра с осью и проходит через . Чтобы задать такие прямые, построим касательную плоскость к цилиндру, которая содержит — в силу симметрии их будет две . В итоге нам подойдут все . Нетрудно видеть, что в случае равенства плоскости просто совпадают.