Тригонометрия на Росатоме —Каталог задач по Олимпиадной математике

Главная
Каталог задач
Каталог заданий по Олимпиады - Математика
Тригонометрия на Росатоме

Тема Росатом

Тригонометрия на Росатоме

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела росатом

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#83306

Решить уравнение

x x 4cosπx =[lg(100 ⋅3 )]− [lg[3]]

Здесь $[a]$ – целая часть числа $a$ – наибольшее целое число, не превосходящее $a$ .

Источники: Росатом - 2024, вариант регионов, 11.2 (по мотивам ММО - 2020, 11.2 второго дня)

Подсказки к задаче

Подсказка 1

Сразу, как мы видим логарифмы, надо записывать ОДЗ. ОДЗ здесь будет x >= 0. Дальше, давайте сделаем тождественные преобразования. У нас выходит, что 4cos(pi * x) - 2 = [lg(3^x)] - [lg[3^x]]. Попробуйте посмотреть чему вообще может равняться правая часть. Как нам оценить 3^x (по сути из этой оценки и вытекает значение правой части)?

Подсказка 2

Для любого x можно найти такое k, что 10^(k + 1) > 3^x >= 10^k, k - целое. При этом эта оценка работает и на [3^x] с тем же k. Значит, правая часть всегда 0. Что теперь остаётся сделать?

Подсказка 3

Верно, решить уравнение 4cos(pi * x) = 2 с учетом ОДЗ. После понятных преобразований, нужно получить две серии решений, каждая из которых зависит от периода, и понять для каких периодов x >= 0.

Показать ответ и решение

Запишем ОДЗ

x x [3 ]≥1 =⇒ 3 ≥ 1 =⇒ x ≥0

Сделаем преобразования:

x x 4cosπx = [lg(100 ⋅3 )]− [lg[3 ]]

4cosπx= 2+ [lg(3x)]− [lg[3x]]

Докажем, что $[lg(3x)]− [lg[3x]]= 0.$ Пусть $[lg(3x)]= k,$ тогда $10k+1 > 3x ≥ 10k.$ Если взять целую часть, то получим $10k+1 > [3x]≥10k.$ То есть "перескочить"через целое невозможно, то есть в действительности $[lg(3x)]− [lg[3x]]= 0.$

Тогда получаем

4cosπx= 2 =⇒ cosπx= 1 2

⌊ ⌊ πx = π+ 2πk | x= 1 +2k ||⌈ 3 ⇐⇒ || 3 πx =− π+ 2πn ⌈ x= − 1+ 2n 3 3

С учетом ОДЗ получаем

⌊ x= 1 +2k, k ∈ℤ, k ≥0, || 3 |⌈ 1 x= − 3 + 2n, n∈ ℤ, n≥ 1

Ответ:

$1 +2k, k ∈ℤ, k≥ 0, 3$ $− 1+ 2n, n∈ ℤ, n≥ 1 3$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#83297

Известно, что

----sin2x----- -----cosy----- ------1------ 1+ cosy− sin2x =1 − cosy+ sin2x = sin2x+ cosy− 1

Найти максимум $cos22x+ sin2y$ .

Подсказки к задаче

Подсказка 1

Когда видишь выражение с тригонометрией и дробями, то становится страшно. Но от одного из этого точно можно избавиться и записать систему из трёх уравнений.

Подсказка 2

Уравнения всё ещё не выглядят красиво, но может, тогда их получится разложить на множители?

Подсказка 3

В знаменателях первой и второй дроби есть одинаковое выражение в виде разности некоторого синуса и некоторого косинуса. После домножения на знаменатель это разность может стать одним из множителей. А ещё совсем нетрудно раскладывается на множители выражение получаемое из равенства первой и третей дробей (вспомните про разность квадратов).

Подсказка 4

Тогда получается 4 случая. 3 из них нетрудные. Но случай, когда в обоих выражениях sin2x + cosy + 1 = 0, не так прост. Искомое выражение удобно было бы свести к виду "число = квадрат какого-то выражения", так как это даёт нам хорошую оценку из-за неотрицательности квадрата.

Показать ответ и решение

Преобразуем равенство первого и второго выражений (домножим на знаменатели, приведём подобные и разложим на множители):

(sin2x− cosy)(sin2x +cosy+1)= 0

Аналогично сделаем с равенством первого и третьего выражений:

(sin2x− 1)(sin2x+ cos+1)= 0

Рассмотрим $4$ случая:

$1)sin 2x =cosy$ и $sin2x= 1$ . В этом случае $cos22x +sin2y =0$ .

$2)sin 2x =cosy$ и $sin2x+ cosy +1= 0$ , тогда $sin2x= cosy = − 1 2$ и $cos22x +sin2y = 3 2$ .

$3)sin 2x +cosy+1 =0$ и $sin2x= 1$ . Тогда $cosy =− 2$ , что невозможно.

$4)sin 2x +cosy+1 =0$ . Запишем $cos22x+ sin2y$ как $2− sin22x− cos2y$ . Теперь вместо $sin2x$ подставим $− 1− cosy$ и преобразуем: $1− 2cosy− 2cos2y = 3− 1(1+2 cosy)2 2 2$ . Видно, что максимум равен $3 2$ и он достигается при $cosy =− 1 2$ . Осталось заметить, что $cosy = sin2x= − 1 2$ не зануляют знаменатели в изначальных равенствах.

Ответ:

$3 2$

Ошибка.
Попробуйте повторить позже

Задача 3#75111

Решите уравнение

logsinxsin2x+ logsin2x sin3x+ logsin3x sinx=

=logsin2xsinx +logsin3xsin 2x +logsinxsin3x

Источники: Росатом-2023, 11.2, региональный (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Что первым делом нужно написать в уравнении с логарифмами?

Подсказка 2

Конечно, ОДЗ! Само уравнение выглядит довольно страшно, но не видите ли вы в нём много похожего?

Подсказка 3

Подумайте, как можно выразить все логарифмы из правой части через логарифмы в левой части. Тогда можно будет ввести замену: заменяем первый логарифм, второй... а третий ведь можно выразить через первые два!

Подсказка 4

Получили красивое уравнение, но, правда, с двумя переменными... Не спешите пугаться! Его можно разложить на скобочки :) Останется только решить получившуюся совокупность, не забыв учесть ОДЗ и ограничение на знаменатель

Показать ответ и решение

Областью определения функций, входящих в исходное уравнение, являются значения $x$ , при которых $sinx ∈(0;1),sin2x∈ (0;1),sin3x∈$ $(0;1).$

Положим $u =logsinx sin2x$ и $v = logsin2x sin3x$ . Тогда, по формулам перехода от одного основания логарифма к другому имеем

logsinxsinx 1 1 logsin2xsinx = logsinxsin2x = logsinx-sin2x = u,

logsin3xsinx = logsin2xsinx-= -1. logsin2x sin3x uv

Далее, аналогично, $log sin2x= 1 sin3x v$ и $log sin3x= uv sinx$ . После этого исходное уравнение запишется так:

1- 1 1 u+ v+ uv = u + v + uv.

Перенося все члены из левой части уравнения в правую и выполняя стандартные преобразования, получаем

v+-u+-u2v2-− u2v−-uv2− 1 (u-+v)−-uv(u+-v)+(u2v2−-1)- uv = uv = = (u+-v)(1−-uv)+-(uv− 1)(uv-+1)= (uv−-1)(uv−-u− v-+1)= uv uv = (uv−-1)(u(v− 1)−-(v-− 1))= (uv− 1)(1-− u)(v-− 1)= 0. uv uv

Поэтому решениями преобразованного уравнения являются все значения $u$ и $v$ , удовлетворяющие хотя бы одному из равенств $u= 1$ , или $v =1$ , или $uv = 1$ при условии (это относится только к первым двум равенствам) $uv ⁄= 0$ .

Возвращаясь к исходному уравнению отсюда следует, что с учётом области определения, его решениями являются решения совокупности

u= logsinxsin2x =1,v = logsin2xsin3x= 1,uv =logsinx sin3x= 1.

Эта совокупность на области определения эквивалентна совокупности уравнений

sinx =sin2x,sin2x =sin 3x,sinx =sin 3x.

Рассмотрим первое уравнение совокупности:

sinx= sin2x⇔ sin x− sin2x= 0⇔ sinx− 2sinxcosx= 0⇔ sinx(1− 2cosx)= 0.

Это уравнение на области определения решений не имеет.

Рассмотрим второе уравнение совокупности:

sin2x= sin3x⇔ sin 3x − sin 2x =0 ⇔ 3x − 2x 3x+ 2x x 5x sin --2--cos--2---= sin2 cos 2-= 0.

Решения уравнения $sin x2 = 0$ в область определения не входят. Решениями уравнения $cos5x2-= 0$ являются $52x= π2 + πk,k$ — целое, т.е. $x = π5 + 2π5-k$ . При $k$ кратном $5$ такие $x$ принадлежат области определения, при остальных значениях $k$ - нет.

Рассмотрим третье уравнение совокупности:

sinx= sin3x⇔ sin 3x − sin x= 0⇔ sin 3x−-xcos 3x-+x-= sinxcos2x =0. 2 2

Решения уравнения $sinx =0$ в область определения не входят. Если $cos2x= 0$ , то $sin 2x =±1$ , поэтому решения уравнения $cos2x= 0$ в область определения также не входят.

Ответ:

$π + 2πn,n∈ Z 5$

Ошибка.
Попробуйте повторить позже

Задача 4#68075

Решить уравнение

( 4 )( 4 ) 2 2 sin 5x+ 1 sin 3x +1 = 4sin 5x⋅sin 3x

Источники: Росатом-2023, 11.2, Москва (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Мы видим, что относительно замены a=sin^2(5x), и b=sin^2(3x) уравнение симметрично. Попробуйте оценить каждую из скобок снизу по отдельности и подумать, что это дает(размышления про симметрию нужны, так как, вероятно, нужно как-то по одному алгоритму оценивать каждую из скобок).

Подсказка 2

Верно, мы можем оценить, что первая скобка - это хотя бы 2sin^2(5x), а вторая - хотя бы 2sin^2(3x) (так как t^2+1>=2t - по неравенству о средних или просто можно перенести в левую часть все). Значит, левая часть почти всегда больше или равна правой. Что это дает нам? Какая система из этого следует?

Подсказка 3

Действительно, у нас выходит, что sin^2(3x)=sin^2(5x)=1 А это значит, что |sin(3x)|=1=|sin(5x)|. Остается решить эту систему и получить ответ.

Показать ответ и решение

Выполним равносильные преобразования в исходном уравнении:

4 4 4 4 2 2 sin 5x ⋅sin 3x +sin 5x+ sin 3x+ 1− 4sin 5x⋅sin 3x = 0

(sin45x⋅sin43x− 2sin25x⋅sin23x+ 1)+ (sin45x − 2sin25x ⋅sin23x +sin43x)= 0

(sin25x⋅sin23x− 1)2+ (sin25x − sin23x)2 = 0

Сумма неотрицательных слагаемых равна нулю тогда и только тогда, когда каждое слагаемое равно нулю. Тогда

( {sin25x⋅sin23x− 1= 0 (sin25x− sin23x= 0

Учитывая ограниченность синуса, имеем

( ( π ( π πn { |sin5x|=1 |{ 5x= 2 +πn |{ x= 10 +-5 ,n ∈ℤ ( |sin3x|=1 ⇔ |( 3x= π +πm ⇔ |( x= π + πm-,m ∈ℤ 2 6 3

Далее находим пересечение серий

({ π-+ πn = π+ πm-⇔ 3n− 5m =1 ⇔ n =2 +5k ,k ∈ℤ 10 5 6 3 (m = 1+3k

Окончательно получаем $π x= 2 + πk,k ∈ℤ$

Ответ:

$π + πk,k ∈ℤ 2$

Ошибка.
Попробуйте повторить позже

Задача 5#76647

На плоскости отмечено множество точек $M,$ координаты $x$ и $y$ которых связаны соотношением

sin(2x +3y)= sin2x+ sin3y.

Круг радиуса $R,$ расположенный на той же плоскости, не пересекается с множеством $M.$ Какие значения может принимать радиус такого круга?

Источники: Росатом-2023, 11.5 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Не очень удобно работать с синусами от разных аргументов. Может, попытаться расписать сумму синусов?

Подсказка 2

Что будет, если посмотреть на левую часть как синус двойного угла?

Подсказка 3

Получилось, что нужно разобрать 3 случая, и нарисовать их, для того чтобы понять, какие радиусы нам подходят

Показать ответ и решение

В левой части равенства применим формулу синуса двойного угла, а в правой части применим формулу суммы синусов:

2x+ 3y 2x+ 3y 2x+ 3y 2x − 3y 2sin---2--cos--2---= 2sin--2---cos--2---

2x+ 3y( 2x+ 3y 2x− 3y) 2sin---2-- cos--2---− cos---2-- =0

−4sin 2x-+3ysin3ysinx =0 2 2

Случай 1: $sin2x+3y-= 0⇒ 2x+ 3y =2πk,k∈ ℤ (1) 2$

Случай 2: $sin3y= 0⇒ y = 2πk,k∈ ℤ (2) 2 3$

Семейство горизонтальных прямых на плоскости с уравнениями $(2)$ принадлежат множеству $M.$

Случай 3:

$sinx= 0,y− любое ⇒ x= πk,k ∈ℤ.(3)$

Семейство вертикальных прямых на плоскости с уравнениями $(3)$ принадлежат множеству $M.$ Семейство прямых разбивает плоскость на равные прямоугольные треугольники с катетами $π$ и $2π: 3$

$PIC$

Радиус круга, вписанного $△ABC,$ равен $5−√613π.$ Если радиус круга, не имеющего с $M$ общих точек, имеет радиус $R ≥ 5−√613π,$ то его центр принадлежит одному из треугольников разбиения, а окружность его границы имеет общие точки со сторонами треугольника. Таким образом, радиус такой окружности меньше радиуса вписанной окружности.

Ответ:

$( 5− √13 ) 0;--6---π$

Ошибка.
Попробуйте повторить позже

Задача 6#76629

Координаты $(x;y)$ точек в квадрате ${(x;y):0≤x ≤2π,0≤ y ≤ 2π}$ удовлетворяют системе уравнений

{ sin x+siny = sin1 cosx +cosy = cos1

Сколько таких точек находится в квадрате? Найти координаты $(x;y)$ наиболее удаленной точки от центра квадрата.

Источники: Росатом-2022, 11.2 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Кажется, что если поскладывать и повычитать уравнения из этой системы, то они смогут свернуться по известным нам тригонометрическим формулам, возможно, только стоит домножить их предварительно на что-то.

Подсказка 2

Попробуйте домножить первое уравнение на сos(1), второе на sin(1) и вычесть, а также умножить первое на sin(1), второе на cos(1) и сложить, в первом случае так мы избавимся от противных sin(1), cos(1), а во втором заменим их на 1, поработайте с полученными уравнениями.

Подсказка 3

Мы получили sin(x-1) = sin(1-y), cos(x-1) + cos(y-1) = 1, первое легко решается и может дать нам условия на корни, которые можно использовать во втором.

Показать ответ и решение

Умножаем первое уравнение на $cos1,$ второе — на $sin 1$ и вычитаем результаты:

(sinx+ siny)cos1− (cosx+ cosy)sin1 =0

(sinx cos1− cosxsin 1)+ (sinycos1 − cosysin1)= 0

sin(x− 1)+ sin(y− 1)= 0

sin(x− 1)= sin(1− y)

[ x− 1= 1− y+2πk x− 1= π− 1+ y+2πm

Умножаем первое уравнение на $sin1,$ второе — на $cos1$ и складываем результаты:

(sinx+ siny)sin1+ (cosx+ cosy)cos1 =1

(cosxcos1+ sinxsin 1)+ (cosycos1+sinysin1)= 1

cos(x− 1)+ cos(y− 1) =1

Из последнего равенства и первого уравнения совокупности имеем

⌊ y = π+ 1+ 2πs 2cos(y− 1)= 1⇒ cos(y− 1) =cosπ ⇒ |⌈ 3 3 y = 1− π+ 2πl 3

Из первой серии условию задачи удовлетворяет только $y1 = π + 1, 3$ из второй серии — только $y2 =1 + 5π . 3$ Им соответствуют серия $x1 = 2− y1+2πk,$ содержащая единственное значение $5π x1 = 1+ 3 ,$ и серия $5π- x2 = 2− y2+ 2πk ⇒ x2 = 1− 3 + 2πl$ также содержащая единственное значение $π x2 = 1+ 3.$

Случай соответствующий второму уравнению первой совокупности не реализуется, поскольку получаем противоречие

{ cos(x− 2)= − cos(y− 2) ⇒ 0= 1 cos(x− 2)+cos(y− 2)= 1

Ответ:

$2;(1+ 5π,1+ π),(1 + π ,1+ 5π) 3 3 3 3$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#67504

Решите уравнение $f(x)= √3⋅g(x)$ для

f(x) =sinx +sin 3x +sin 5x +...+sin2021x; g(x)= cosx +cos3x+cos5x+ ...+cos2021x

Источники: Росатом-22, 10.2 (см. olymp.mephi.ru)

Подсказки к задаче

Подсказка 1

Нужно как-то сжать эти выражения, то есть применить телескопическое суммирование. Для этого будет в самый раз умножить и левую, и правую часть уравнения на sin(x) (подумайте, может ли он вообще быть равен нулю), а затем применить формулы произведения синусов и синуса с косинусом.

Подсказка 2

Да, получится уравнение вида 1 - cos(2x) + cos(2x) - cos(4x) ... + cos(2020x) - cos(2022x) = √3 * sin(2022x). Телескоп сработал -> остается перенести синус с косинусом в одну часть, единичку - в другую, а затем вспомнить формулу вспомогательного угла - ведь коэффициенты 1 и √3 так и намекают на это :)

Показать ответ и решение

Такие тригонометрические телескопические суммы сворачиваются домножением и делением на $sinx$ (при этом нужно сказать, что синус ненулевой, потому что числа вида $x= πn,n ∈ℤ$ решениями уравнения не являются). После домножения получим вот что:

sinx⋅sinx+ sinx⋅sin 3x +...+ sinx ⋅sin2021x=

√- = 3(sinx⋅cosx+ sinx⋅cos3x+ ...sinx ⋅cos2021x)

Применим формулы произведения синусов

cos0x−-cos2x+-cos2x-− cos4x-+...+cos2020x−-cos2022x-= 2

√-sin2x+-sin4x−-sin2x+-...+-sin2022x-− sin-2020x = 3 2

Слагаемые удачно взаимноуничтожаются и остаётся

1− cos2022x= √3sin 2022x

√ - --3sin2022x + 1cos2022x= 1 2 2 2

( ) sin 2022x + π = 1 6 2

Откуда $x= πn-,n∈ ℤ 1011$ или $x = -π-+ -πk-,k∈ ℤ 3033 1011$ . Осталось учесть условие $sinx ⁄=0,$ так что $n ⁄=1011m,m ∈ℤ.$

Ответ:

$-πn , π + πk-, n⁄= 1011m, k,n,m ∈ ℤ 10113033 1011$

Ошибка.
Попробуйте повторить позже

Задача 8#79624

При каких целых $n$ функция $f(x)= cosnx ⋅sin 15x- n2$ имеет период $T = 5π$ ?

Подсказки к задаче

Подсказка 1

Нас интересуют случаи, когда период равен 5π. Как можно выразить это условие для нашей функции?

Подсказка 2

Конечно, значения функции в точках x и x+5π будут одинаковы, так что можно приравнять значения функции. Мы получили тригонометрическое уравнение, которое приводится к виду "произведение трёх множителей = 0" (обратите внимание, что значение косинуса зависит от значения аргумента, так что тут нужно отдельно разобрать два случая). Обычно после этого достаточно просто найти, когда зануляется каждый множитель, но помните, что наша задача - не найти такие x, а выяснить, при каких n выражение зануляется для любых аргументов.

Подсказка 3

Подумайте, при всех ли x значение наших тригонометрических функций может обращаться в 0? Если мы можем выразить x через n, π и k, то можем найти и отношение х к π. Что мы можем сказать о его рациональности?

Подсказка 4

Конечно, у нас получится, что х/π — рациональное число. Но мы всегда можем подобрать такой х, что х/π будет иррациональным числом (например, х=π²). То есть при некоторых х такое выражение всегда ненулевое. Тогда остаётся выяснить, для каких множителей отношение х/π может быть иррациональным, и найти, при каких целых n они могут обращаться в 0.

Показать ответ и решение

Условие задачи равносильно тому, что при всех вещественных $x$

15(x+-5π) 15x- cosn(x+ 5π)⋅sin n2 = cosnx⋅sin n2

(a) если $n$ чётно, то имеем равенство

15(x +5π) 15x cosnx⋅sin---n2---= cosnx ⋅sinn2-

( ) cosnx sin15x+275π-− sin152x = 0 n n

2cosnx⋅cos( 30x-+75π) ⋅sin 75π= 0 2n2 2n2

Найдём нули первых двух косинусов

cosnx =0 ⇔ nx= π +πk (k ∈ℤ) ⇔ x = 1-+ k 2 π 2n n

( ) cos 30x-+75π- =0 ⇔ 30x+-75π-= π+ πm (m ∈ℤ) ⇔ x= n2 + mn2-− 5 2n2 2n2 2 π 60 30 2

В обоих случаях отношение $x$ к $π$ рационально. Поэтому найдется такое значение $x,$ при котором два косинуса не обращаются в ноль (например, $2 x= π$ ). Отсюда следует, что условие задачи равносильно равенству

75π 75π 2 sin2n2 =0 ⇔ 2n2 = πt (t∈ℤ) ⇔ 75= 2n t,

которое не может быть выполнено, так как число $75$ нечетно.

(b) если $n$ нечётно, то имеем равенство

15(x+ 5π) 15x − cosnx ⋅sin ---n2---= cosnx ⋅sin n2-

( ) cosnx sin15x+275π-+ sin152x = 0 n n

2cosnx⋅sin( 30x+-75π)⋅cos75π= 0 2n2 2n2

Найдём нули первых двух множителей

π x 1 k cosnx =0 ⇔ nx= 2 +πk (k ∈ℤ) ⇔ π = 2n-+ n

( ) 2 sin 30x+2n275π- = 0 ⇔ 30x2+n725π-=πm (m ∈ℤ) ⇔ xπ = n3m0-− 52

В обоих случаях отношение $x$ к $π$ рационально. Поэтому найдется такое значение $x,$ при котором два косинуса не обращаются в ноль (например, $x= π2$ ). Отсюда следует, что условие задачи равносильно равенству

75π- 75π π 2 2 cos 2n2 = 0 ⇔ 2n2 = 2 + πt (t∈ℤ) ⇔ 75 =2n t+2n

75 n2 = 2t+ 1

Так как $75 n2$ — целое, то $n2 = 25$ или $n2 =1,$ отсюда

n ∈{−5;−1;1;5}

Ответ:

$±1, ±5$

Ошибка.
Попробуйте повторить позже

Задача 9#48861

При каких $a$ уравнение $arcsin(cosx)=cos(arcsin(x− a))$ имеет единственное решение?

Источники: Росатом-21, 11.5 (см. olymp.mephi.ru)

Показать ответ и решение

Изобразим график $y = arcsincosx$ на $[−π,π]$ . Сама функция имеет период $2π$ , поэтому на остальной прямой график будет повторяться

$PIC$

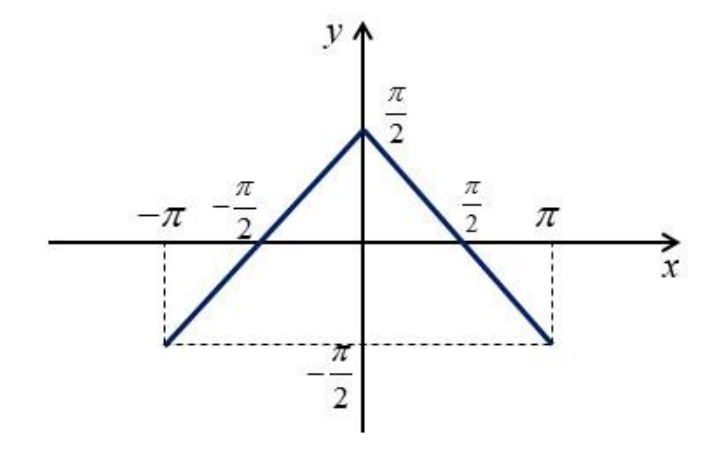
Теперь посмотрим на график правой части $∘ --------2 y = cosarcsin(x− a)= 1− (x− a)$ , который будет полуокружностью

$PIC$

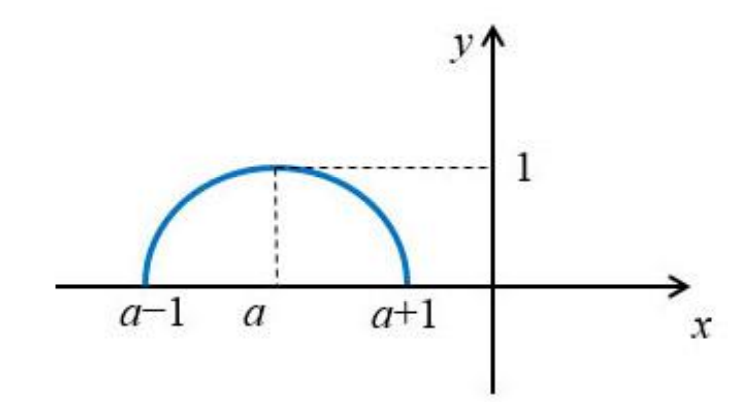
Например, графики будут расположены так при $a0 =− π$

$PIC$

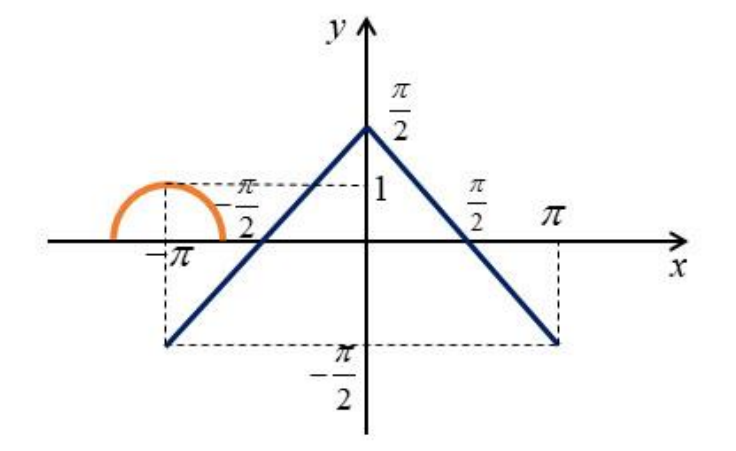
С ростом параметра $a$ оранжевый график перемещается вправо. Достаточно рассмотреть значения $a ∈[−π,π]$ , поскольку оранжевый график может пересекать не более одного “уголка” синего графика (помним про периодичность). Остаётся найти те значения параметра, при которых изменяется количество общих точек на $[−π,π]$ .

Первое такое значение будет в момент первого пересечения при движении оранжевого графика вправо

$PIC$

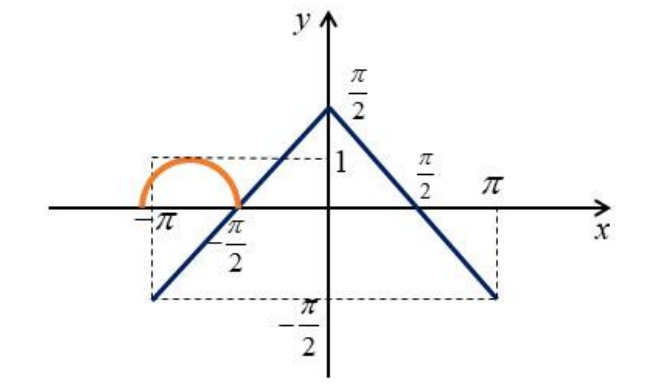
Заметим, что правая точка оранжевого графика соответствует $x= a+ 1$ , откуда

a+ 1= − π ⇐⇒ a1 =− π − 1 2 2

При дальнейшем движении решение будет только одно вплоть до положения

$PIC$

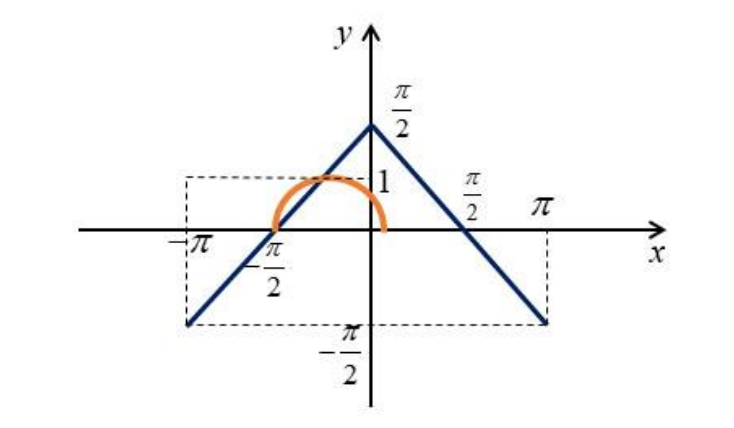
когда решений становится два. Левая точка оранжевого графика соответствует $x= a− 1$ , откуда

π π a− 1= −2 ⇐⇒ a2 =− 2 +1

Дальше решения будет два вплоть до положения, когда произойдёт касание

$PIC$

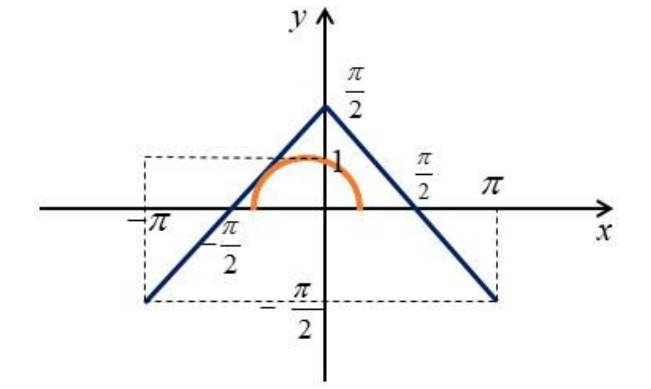
Поскольку касательная имеет коэффициент наклона $− 1$ , то на полуокружности это точка $1 1 (a− √2,√2)$ (учитывая смещение на $a$ из центра координат). При этом точка касания лежит на прямой $π y =x + 2$ (левая часть уголка), откуда

1 1 π π √- √2-= a− √2 + 2 ⇐ ⇒ a3 =− 2 + 2

Далее решений не будет вплоть до касания с противоположной стороны уголка в симметричной точке $a4 =− a3 = π2 − √2$ , где решение будет одно. Далее вплоть до $a5 = −a2 = π2 − 1$ решений два. Потом от неё до $a6 = π2 + 1$ решение единственное, а после до $a7 = π$ решений нет.