Сначала необходимо заметить, что кратчайшее расстояние между двумя расположенными на сфере точками по ее поверхности это длина меньшей дуги, проходящей через эти две точки окружности, центр которой совпадает с центром сферы. Отсюда сразу следует первая оценка на радиус сферы: он не может быть меньше, чем В противном случае длина самой большой окружности, расположенной на сфере, меньше, чем , и длина ее меньшей дуги будет меньше, чем что противоречит условию задачи.

Обозначим радиус сферы за ее центр обозначим буквой Рассмотрим две произвольные точки пусть длина дуги равна отметим, что Из сектора и треугольника имеем:

Из этой формулы следует, что периметр треугольника равен:

Рассмотрим функцию одной переменной:

Тогда что положительно при так как
Обратим внимание, что все три слагаемых, входящих в периметр, являются такого сорта функциями, при этом радиус не может быть меньше, чем 5 и, следовательно, величина во всех трех слагаемых принадлежит полуинтервалу Поэтому периметр треугольника является возрастающей функцией параметра и, следовательно, задача сводится к следующей: найти минимальный радиус сферы, на которой могут быть расположены точки удовлетворяющие данным из условия задачи.
Обоснование того, что минимальный радиус равен состоит из двух тезисов. Во-первых, на сфере радиуса расположить три точки в соответствии с условием задачи можно: достаточно взять экватор сферы, его длина равна что равно сумме данных в условии расстояний. Берем произвольную точку на этой окружности, проходим по часовой стрелке расстояние отмечаем точку B, проходим еще отмечаем точку
Во-вторых, на сфере радиуса, меньшего чем 6, точки расположить не получится. Чтобы это доказать, проведем аналогию с глобусом. Представим себе, что точка это северный полюс планеты радиуса 6. Тогда геометрическим местом точек кратчайшее расстояние от которых по сфере до точки равно будет параллель-«экватор», а геометрическим местом точек кратчайшее расстояние от которых по сфере до точки равно будет параллель в южном полушарии. Максимальное расстояние между точкой с «экватора» и точкой с «южной» параллели как раз равно и будет достигаться в случае, когда эти точки расположены на противоположных меридианах. Любые меридиональные смещения одной из точек, очевидно, уменьшат расстояние между ними. Попытка уменьшить радиус сферы-планеты приведет к тому, что параллели, на которых лежат точки и сместятся ближе к южному полюсу, и максимальное из расстояний между точками с этих параллелей (которое по-прежнему достигается в случае их расположения на противоположных меридианах) уже будет менее, чем Итак, минимально возможный радиус сферы равен 6, откуда получаем ответ:

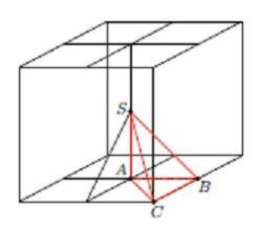
Из условия задачи вытекает, что ребро пирамиды перпендикулярно основанию

Обозначим Пирамида является частью изображённого на рисунке куба с ребром причём все 48 пирамид, образующих этот куб, располагаются центрально-симметрично относительно общей вершины

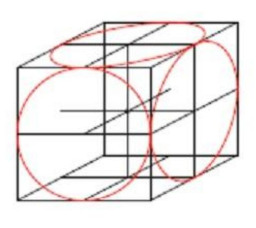
Поэтому искомый объём есть объёма тела, представляющего собой пересечение шара радиуса и данного куба. Это пересечение есть шар без шести шаровых сегментов с высотой шарового сегмента (см. рисунок).

Объём этого тела:

Значит, искомый объём равен

Отметим, что объём всей пирамиды равен (или, что то же самое, части куба, то есть ) Найденный объём части пирамиды больше, чем объема пирамиды, так как

Это подтверждает, что мы нашли именно объём большей части пирамиды.

Поскольку высота пирамиды видна из вершин и под одним и тем же углом, точка лежит на медиане (она же биссектриса и высота) треугольника или её продолжении. Если , и , а искомый угол , то имеем

откуда, подставляя данные задачи, получаем , в зависимости от того, лежит ли точка внутри треугольника или вне него. Значит, или

Пусть это пирамида , где (то есть основанию перпендикулярны и ). Обозначим сторону квадрата из основания за .

В силу симметрии высоты и к пересекаются в одной точке. Тогда из условия , как угол между высотами к общей прямой двух плоскостей. Далее в силу той же симметрии и , то есть и . Отсюда . Далее заметим, что , поскольку перпендикулярна двум прямым и , откуда . Тогда . Тогда . Осталось найти

То есть высота пирамиды равна стороне основания.

Центр сферы равноудалён от точек на её поверхности, а раз по условию вершины основания принадлежат сфере, то центр сферы является центром описанной около основания окружности.

Пусть сфера пересекает ребро в точке . Тогда равны радиусы Опустим перпендикуляр к ребру , он является медианой равнобедренного треугольника Обозначим сторону основания через и пусть угол Пусть основание перпендикуляра, проведенного из точки на сторону

Находим из правильного треугольника в основании , а так как это линейный угол двугранного угла и равен , то

Также заметим

Тогда получаем

(так как

В итоге так что сфера делит в отношении

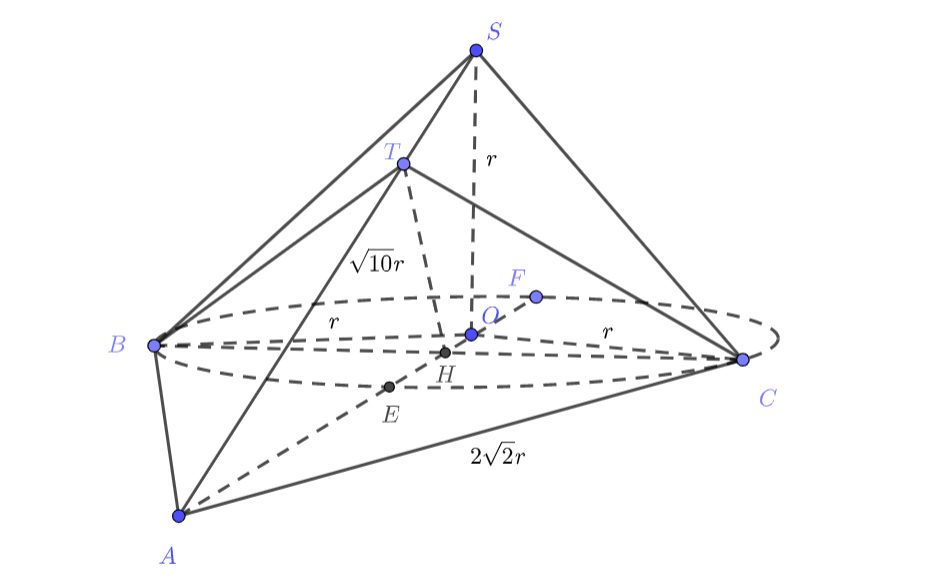
Пусть центр основания радиуса — точка , точка рядом , а — вершина конуса. Пусть также пересекает окружность в . Касательные плоскости содержат касательные из к окружности, пусть это и . Легко видеть, что и и есть искомые плоскости, проведём в этих треугольниках высоты к , которые в силу симметрии упадут в одну точку . Тогда наша задача сводится к поиску .

Итак, будем искать отрезки и . По теореме об отрезках касательной и секущей

Здесь мы просто посчитали площадь прямоугольного треугольника двумя способами. Теперь заметим, что , поскольку две прямые ей перпендикулярны, откуда , то есть , как прямоугольные с общим углом. Имеем

В итоге .

Опустим перпендикуляры из точки на плоскости и соответственно. Обозначим , , Согласно условию составим систему уравнений

Отсюда находим , , Обозначим длины рёбер , и через и соответственно.

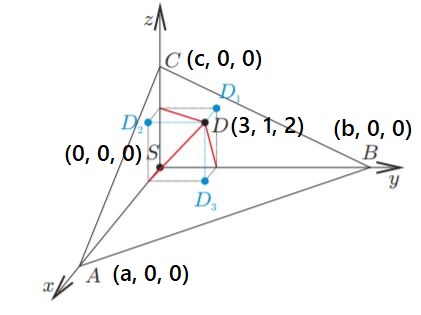
Лемма:

Доказательство: Введём систему координат с началом в точке как на рисунке. Запишем уравнение плоскости .

Так как плоскость не проходит через начало координат, то . Значит можно поделить на . Получим:

Теперь поставим в уравнение плоскости точки, в ней лежащие, чтобы найти коэффициенты , , . Итого получим, что , , . А значит уравнение плоскости

Подставив туда координаты принадлежащей этой плоскости точки , получим Лемма доказана.

Из неравенства между средним арифметическим и средним геометрическим для трёх переменных получаем:

причём равенство имеет место при Объём пирамиды поэтому Равенство имеет место при , ,

Примем сторону тетраэдра за 12. Угол будем искать через косинус, который равен отношению площади треугольника проекции треугольника на плоскость основания, к площади самого треугольника - сечения. Площадь проекции определяется несложно, так как вершины делят соответствующие радиусы описанной окружности основания (площадь основания ) в тех же отношениях как и соответствующие им точки делят боковые стороны тетраэдра.

Стороны сечения будем вычислять по теореме косинусов: . Теперь вычислим площадь сечения. Косинус угла , лежащего напротив стороны равен . Тогда . Для площади сечения получим следующий результат . Теперь последнее действие:

Площадь боковой грани , по условию, не меньше С другой стороны, она равна

Следовательно, , т.е. перпендикулярно . Аналогично получаем, что и перпендикулярно и . Поэтому объём пирамиды равен

Пусть — общая вершина рассматриваемых конусов, и — их оси. Обозначим через и их общие образующие и через искомый угол . Описанная в задаче конфигурация имеет две плоскости симметрии: одна — — содержит оси конусов, другая — — содержит из образующие. Тогда эти плоскости перпендикулярны. Пусть прямая их пересечения.

Обозначим через угол в осевом сечении каждого из конусов. Так как является образующей для конуса с осью и наоборот, то . Кроме тогда, и .

Будем считать, что точки лежат в некоторой плоскости, перпендикулярной прямой и расположенной на расстояние от вершины . Тогда из пирамиды , в которой все плоские углы при вершине прямые, имеем

Тогда по теореме косинусов для треугольников и

Приравняем эти 2 выражения и домножим на квадраты косинусов.

Мы знаем, что , поэтому

(a) У нас есть 2 грани со стороной 2, но вместе с 2 треугольник может образовать только 4 и 5?!

(b) У нас есть 2 грани со стороной 2. Вместе с 2 треугольник может образовать только 4 и 5 или 11,1 и 13. Значит противоположная сторона равна 9. Пусть нам дан тетраэдр и , , . Тогда и по неравенству треугольника для сторона . Значит последняя сторона . По формуле Герона площадь равна . Тогда если высота в этом треугольнике, то . По теореме Пифагора и . Отсюда следует, что лежит на отрезке

Аналогично, , высота в этом треугольнике длиной , , Значит, лежит на луче за точку . Отсюда

Вспомним, что у нас есть такое неравенство на

Оно выводится так: спроецируем всё на плоскость, перпендикулярную пусть — проекция , — проекция , — проекция и . Так как и перпендикулярны , то и Значит, проекция на эту плоскость длиной от до , а проекция на прямую это Значит,

Подставим числа и получится, что так как , а , то

Пусть у некоторой правильной пирамиды известно боковое ребро . Давайте посчитаем при какой дине стороны основания пирамиды будет обладать наибольшим объемом.

Теперь это функция от . Возьмем производную по . Она зануляется при и в этой точке производная меняет свой знак с + на -. Значит это точка максимума и объем максимальный при .

Вернемся к задаче. Пирамида, вершинами которой служат точки касания и центр сферы, является правильной треугольной пирамидой с ребром . Значит, чтобы объем был максимальным, нужно добиться того, чтобы сторона ее основания была .

Из точек и проведем перпендикуляры к , в силу симметрии они попадут в одну точку .

По доказанному ранее и при этом . Значит , но тогда угол прямой, а его нам и нужно было найти.

Пусть высоты из вершины на грань , а из вершины на грань . Тогда так как тетраэдр правильный, то и пересекаются на стороне в tt середине . Пусть . Тогда

Поскольку равносторонний, то .

Так как , то

Функция достигает максимуму при и может быть бесконечно близко к 0, поэтому площадь может быть в интервале .

Поскольку около параллелепипеда описана сфера, этот параллелепипед — прямоугольный. Обозначим его рёбра, исходящие из одной вершины, через , и . Диагонали параллелепипеда равны диаметру описанной сферы, а объём равен . Из условия задачи следует, что .

По неравенству Коши:

Так как равенство достигается только в случае , то и площадь поверхности:

Так как пирамида правильная, то в основании лежит квадрат с диагоналями , пусть — его центр. Тогда является высотой пирамиды, так что из условия про косинус находим

Плоскость сечения параллельна , поэтому содержит параллельную прямую из плоскости . Поэтому сечение может быть двух видов:

1 случай) треугольник , где лежит внутри .

Тогда (строго меньше единицы, потому что сечение параллельно , содержать не может). Пусть .

Теперь найдём, чему равняется (то есть радиус вписанной окружности)

2 случай) Пятиугольное сечение плоскостью , где лежит внутри . Заметим, что и поэтому и

Пусть

Тогда из подобий и получаем

Значит,

Также имеем

Откуда

Так как

. Тогда по теореме Пифагора .

Воспользуемся формулой

Тогда