Ошибка.
Попробуйте повторить позже
Таблица покрашена в несколько цветов (каждая клетка — ровно в один цвет) так, что в любом квадрате
присутствуют
клетки не более чем трёх различных цветов. Какое наибольшее количество цветов могло быть использовано?
Источники:
Подсказка 1
Раз у нас в каждом квадрате 2 на 2 не более трех различных цветов, то в каждом из них есть цвет, клеток которого хотя бы две в квадрате. Может, тогда стоит рассмотреть сколько может быть квадратов, в котором хотя бы две клетки конкретного цвета?
Подсказка 2
Попробуйте пойти таким путем: для начала найдите 4 квадратика, в которых по одной клетке такого цвета (а возможно их меньше, но считайте что 4), А после оцените кол-во квадратиков, в которых хотя бы 2 клетки этого цвета с помощью разного подсчета кол-ва клеток этого цвета во всех квадратиках)
Подсказка 3
В итоге выйдет хорошая оценочка на кол-во квадратиков, в котором конкретного цвета хотя бы 2. А теперь вспоминаем, что у нас все квадратики такие, что в них есть цвет, которого хотя бы два. Остается посчитать кол-во квадратов, предположить что цветов всего C, и пользоваться оценкой)
Подсказка 4
Если немного сложно пользоваться полученной оценкой, то попробуйте сложить все полученные оценки для всех цветов, а также вспомнить, что сумма всех кол-в клеток конкретного цвета - это кол-во всех клеток)
Оценка. Сначала сформулируем и докажем следующую лемму:
Лемма. Пусть — количество клеток некоторого цвета
Тогда существует не более
квадратов
в которых клеток
этого цвета хотя бы
Доказательство. Прежде всего отметим, что каждая клетка этого цвета находится в четырех квадратах Внимательный
читатель заметит, что эти квадраты могут выходит за границы доски, но поскольку мы оцениваем количество квадратов
в которых
клеток этого цвета хотя бы
сверху (даже если при оценке некоторые такое квадраты выходят за доску, то все равно оценка справедлива),
то это замечание не повлияет на доказательство. Рассмотрим самую левую клетку этого цвета, находящуюся на самой нижней горизонтали
доски, в которой есть этот цвет. Понятно, что квадрат, в котором эта клетка является правой верхней, не может больше содержать
клеток этого цвета. Аналогично для самой правой клетки нижнего ряда (которая, вообще говоря, может совпадать с самой
левой клеткой этого ряда) квадрат, в котором она является левой верхней, не может больше содержать клеток этого цвета.
Такие же рассуждения можно провести с самым верхним горизонтальным рядом (который, опять же, может совпадать
с самым нижним). Таким образом, есть хотя бы
квадрата
в которых присутствует только одна клетка цвета
Теперь рассмотрим все квадраты которые содержат цвет
Так как каждая клетка этого цвета находится в четырех квадратах,
то суммарно в них находятся
клеток цвета
(некоторые из квадратов, возможно, выходят за границы таблицы). Пусть количество
квадратов, в которых хотя бы две клетки этого цвета, равно
Тогда, так как есть хотя бы
квадрата
в которых присутствует
только одна клетка цвета
то получим:
Пусть количество цветов равно Существует ровно
квадратов
которые накладывают условие на цвета. Тогда
для каждого квадрата
должен найтись цвет, клеток которого в нём хотя бы
а из всего
то просуммируем
количество квадратов
в которых клеток цвета
хотя бы
для всех
и оценим их количество сверху, пользуясь
леммой:
Но так как каждая клетка покрашена в один цвет:
Значит,
Пример. Рассмотрим все возможные вертикальные полоски. В первой из них покрасим все клетки в различные цвета. Во второй - в один
и тот же новый цвет. В третьей - снова все клетки в новые различные цвета, потом снова в один новый цвет и так далее. При этом клеток в
полосках с нечётным номером всего а полосок с чётным номером ровно
поэтому различных цветов ровно
Также понятно, что в любом квадрате
встретятся две клетки из вертикальной полоски с чётным номером.
Значит, они будут одинакового цвета, т. е. цветов в каждом квадрате
будет не больше
(на самом деле, ровно
Ошибка.
Попробуйте повторить позже
В каждой клетке квадратной таблицы размером написали по действительному числу, по модулю не превосходящему
Оказалось, что сумма всех чисел равна нулю. Для какого наименьшего
можно утверждать, что в какой-то строке или каком-то столбце
сумма чисел заведомо окажется по модулю не превышающей
Источники:
Сначала покажем, что не подойдет. Разделим таблицу на четыре квадрата
Правый верхний квадрат заполним числами
а левый нижний - числами
Остальные клетки заполним нулями. Легко видеть, что в каждой строке и в каждом столбце сумма
равна
Теперь покажем, что подходит. Предположим, что для некоторой таблицы это не так, то есть суммы во всех её строках и
столбцах оказались либо больше
либо меньше
Заметим, что можно менять местами строки в таблице, не нарушая это свойство
и условие задачи.
Поменяем местами строки так, чтобы их суммы убывали сверху вниз. Разделим таблицу на две половины верхнюю и
нижнюю. Заметим, что либо в верхней половине все строки имеют положительную сумму, либо в нижней - все отрицательную. Тогда в
одной из половин сумма по модулю больше
Так как общая сумма всех чисел равна нулю, то в другой половине сумма такая же по
модулю и противоположная по знаку.
Теперь отсортируем столбцы так, чтобы их суммы убывали слева направо. (Суммы в строках при этом не поменяются.) Аналогично,
суммы в правой и в левой половине таблицы оказались по модулю больше
Разобьем таблицу на четыре квадрата суммы в них обозначим за
| | |
| | |
Заметим, что
Это означает, что одно из чисел или
по модулю превосходит
Но в каждом из соответствующих квадратов всего
клеток, и числа в них по модулю не превосходят
Противоречие.
Ошибка.
Попробуйте повторить позже
Последовательность различных клеток клетчатого квадрата
называется циклом, если, во-первых,
, и, во-вторых,
клетки
и
являются соседними по стороне при всех
(считаем при этом, что
). Множество
клеток
квадрата назовём разделяющим, если в любом цикле есть хотя бы одна клетка из множества
. Найдите наименьшее вещественное число
такое, что для любого натурального числа
в квадрате
существует разделяющее множество из не более чем
клеток.
Источники:
Для построения примера разделяющего множества, в котором не более чем клеток, раскрасим все клетки в три цвета по
диагоналям: первую диагональ - в первый цвет, вторую - во второй, третью - в третий, четвертую - опять в первый, и так
далее.
![]()
Любой цикл из клеток, как легко видеть, пересекает как минимум три соседних диагонали и, следовательно, содержит клетки всех
трех цветов. Клеток одного из цветов будет не более , и этот цвет можно использовать в качестве разделяющего
множества.
Оценка. Покажем, что никакое не подходит.
Для этого построим граф, вершинами которого являются клетки. Две клетки соединим ребром, если они являются соседними. Получим
граф, в котором вершин и
ребер, при этом циклы задачи находятся во взаимно однозначном соответствии с циклами в
графе. Требуется удалить несколько вершин так, чтобы в оставшемся графе не было циклов.
Предположим, мы удалили вершин. Если в оставшемся графе нет циклов, то этот граф является объединением деревьев и в
нем не более чем
ребро. При этом из каждой удаленной вершины выходило не более 4 ребер, и всего было удалено было не более
ребер. Таким образом, имеем неравенство
откуда
что невозможно при и достаточно большом
.
Ошибка.
Попробуйте повторить позже
Натуральные числа записаны в клетках таблицы
так, что для всех
числа
и
находятся в
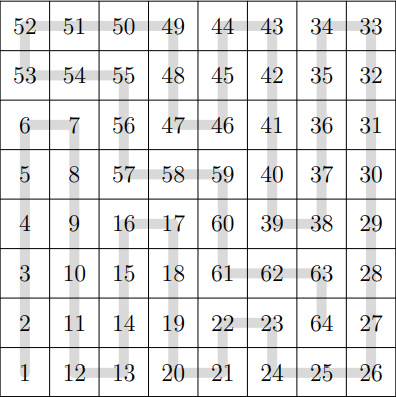
соседних по стороне клетках. Каково максимальное значение возможной суммы чисел на главной диагонали?
Оценка. Раскрасим клетки таблицы в шахматном порядке так, чтобы клетки на выбранной главной диагонали были белыми. Не умаляя
общности, можно считать, что единица стоит не выше диагонали. Найдем максимальное значение наименьшего числа, попавшего на
диагональ. Поскольку соседние числа стоят в клетках разного цвета, а белых клеток под диагональю находится всего то одно из чисел
от
до
обязательно попадает на диагональ. Остальные числа на диагонали гарантированно имеют одну четность, поэтому их сумма
не превосходит суммы четных чисел от
до
В итоге заключаем, что для суммы чисел на диагонали есть оценка
сверху:
Пример подходящей расстановки:
Ошибка.
Попробуйте повторить позже
На клетчатой доске расставили
белых и
черных ладей так, что ладьи разных цветов не бьют друг друга. При
каком наибольшем
такое возможно?
Источники:
Подсказка 1!
1) Итак, нам нужно оценить возможное количество ладей. Так как мы знаем количество строк и столбцов, было бы логично оценить количество ладей через строки и столбцы, на которых они стоят. Ведь если в строке 1 стоят ладьи, и в столбцах 5 и 7, например, то ладей на больше чем 1*2 ( клетки пересечения столбцов и строк, где замечены ладьи). Пусть белые ладьи заняли a клеток и b столбцов...
Подсказка 2!
2) Ага, оценим белые через ab, а черные через оставшиеся столбцы на оставшиеся строчки, и подумаем, как n соотносится с этими оценками на количество ладей...
Подсказка 3!
3) Ну, конечно! n меньше, чем обе наших оценки. Теперь можно попробовать порасставлять ладей и понять, какую оценку мы хотим доказывать. А можно помедитировать над уравнением, и заметить, что если n меньше чем минимальная из оценок, то максимум n достигается, если обе оценки равны! Давайте доказывать, что максимум будет тогда, когда ab равняется оценке на черные ладьи. Чему же равно ab...
Подсказка 4!
4) Ага, k(k+1)! Тогда обе оценки равны, окажем, что это лучший расклад, и не забудем построить пример!
Пусть белые ладьи занимают строк (то есть нашлось ровно
строк, в которых есть белые ладьи) и
столбцов. Белая и чёрная
ладьи не могут стоять в одном столбце или одной строке, потому чёрные занимают не более
строк и
столбцов. Отсюда их количества не превышают соответственно
и
, при этом легко видеть, что
. Далее покажем, что минимум не превышает
. Действительно, пусть, не умаляя
общности
(иначе
). Тогда
(с уменьшением суммы уменьшается и
максимум произведения). То есть
. В качестве примера заполним прямоугольник
в левом верхнем
углу белыми ладьями, затем отразим доску относительно главной диагонали, а потом заполним тот же прямоугольник
чёрными.
Ошибка.
Попробуйте повторить позже
Клетчатая доска раскрашена в шахматном порядке. Какое наибольшее число черных клеток доски можно отметить так, чтобы
не нашлось параллелограмма с вершинами в центрах отмеченных клеток?
Источники:
Подсказка 1!
Попробуем проанализировать условие. Нарисуйте на шахматной доске параллелограмм. Что его существование означает в контексте расстояний между клетками в разных строках..
Подсказка 2!
Да, если нашелся параллелограмм, это значит, что в двух разных строках совпали расстояния между двумя какими-то клетками. Подумайте, какие вообще на доске бывают расстояния. И что каждое встречается не более одного раза.
Подсказка 3!
Но в каждой строке их хотя бы сколько? Давайте посмотрим для фиксированной клетки какой-то расстояния и попробуем оценить количество различных расстояний снизу. А затем и построить пример!
Рассмотрим расстояния между выбранными клетками в каждой строке. Они могут принимать значения При этом если в строке
клеток, то различных расстояний в ней хотя бы
(от крайней клетки до всех). Если в каких-то двух строчках нашлись два равных
расстояния, то
точки образуют параллелограмм, потому такого быть не может. Отсюда каждое расстояние встречается не более одного
раза (рассматривая только
различных из каждой строки). То есть
— сумма числа расстояний по всем строкам и
Осталось привести пример. Для этого выберем все клетки на большой диагонали и на любой из смежных с ней
сторон.


